智能仓储机器人动态路径规划研究

李金钊 张世宣 周小铃 郑潇玥 胡宗政 张勇

摘  要：为解决智能仓储系统中多机器人协同控制问题，提出一种基于预约表障碍地图的改进A*路径规划算法。首先利用预约表生成障碍地图并对机器人进行避障处理;然后给出一种改进A*算法基于障碍地图预约表更新仓储系统中机器人实时位置并实现动态路径规划;最后，基于NImyRIO机器人平台对所提算法进行了实验仿真分析，结果表明所提算法具备一定的可靠性并可提高仓储系统的运行效率。

关键词：智能仓储系统;多机器人系统;路径规划

中图分类号：TP242.6     文献标识码：A

Abstract： In order to solve the problem of coordinately controlling multi robots in intelligent storage system， an improved A * path planning algorithm is proposed based on the obstacle map. First， the reservation table is used to generate the obstacle map， which helps the robots to avoid the obstacles. Then， an improved A * algorithm is proposed to update the real-time position of robot in storage system based on the reservation table of the obstacle map and realize the dynamic path planning. Finally， based on Ni myRIO system， the simulation results show that the algorithm is reliable and can improve the efficiency of the storage system.

Keywords： intelligent storage system; multi robot system; path planning

1   引言（Introduction）

随着物流仓储业的不断发展，由智能机器人所构成的智能化的物流仓储系统成为现代物流产业不可或缺的重要组成部分[1]。目前智能仓储机器人最新研究主要集中于路径规划及多机器人协作等多个方面，在现代仓储物流系统中，多机器人协同运作可极大提高效率，而多机器人动态路径规划是实现多机器人协同前提[2]。关于多机器人的路径规划问题研究由来已久，其主要目标是实现[3，4]：（1）从出发点出发到达预定的目标点;（2）获取无碰撞的安全路径;（3）选取距离最优或者次优路径[5]。路径规划本质上是依据代价最小、路线最短或行走时间最短等优化准则，在工作空间中找一条从起点到目标状态的能避开障碍的最优路径。蚁群算法[6]、D*算法[7]作为智能算法可实现多机器人的动态路径规划，但这两种算法无法得到全局最优路径，难以满足仓储系统运行效率。A*算法[8]是一种常见的全局最优路径规划算法，但传统A*算法作为一种静态路径规划算法，难以直接应用于动态仓储环境，通常需要对其改进以应用于智能仓储系统求解动态路径规划的最优解。本文提出一种改进的A*路径规划算法，并基于NI myRIO所搭建的多机器人平台进行了仿真实验研究，实验结果表明该算法具备运行可靠性，且可提高仓储系统的运行效率。

2  基于改进A*算法的机器人路径规划算法设计（Design of robot path planning algorithm based on improved A* algorithm）

智能仓储系统上货点到卸货点可看作一个点对点系统，智能仓储机器人从接货点到达卸货点，需要完成动态避障和自主路径规划等功能。传统A*算法作为一种启发式搜索算法，只适用于静态地图中点对点循迹，但现代仓储环境中不仅有静止障碍物，还有运行的机器人作为障碍物[9，10]。机器人运行过程中，只有同时避开静态障碍物及运行中的其他机器人才能安全到达目标点[11]。传统的A*算法难以直接应用于现代仓储物流系统，因此，本文提出一种基于预约表和障碍物地图[12]的改进型的A*算法以解决智能仓储动态环境中的多机器人路径规划问题。其主要将复杂环境下仓储机器人的路径规划问题转换为一种连续搜索问题，通过对所有机器人位置的实时获取，生成一张实时的障碍物地图并采用预约表形式予以记录，每台机器人在该预约表地图的基础上进行路径规划，可以有效地防止上述的意外情况的发生。本文主要利用栅格建模法[13]构建环境障碍地图，地图中每个节点为一个可通行单位，而节点之间的黑线忽略不计。在每个节点中植入RFID电子标签用以小车的定位，每个卸货点则定义为关键节点，如图3所示。为保证系统运行稳定性，假设如下：（1）机器人在任意一條道路中只能单向行驶;（2）机器人直行通过一个节点的路径代价为1;（3）每个栅格在同一时刻仅允许通过或容纳一辆小车;（4）机器人运动速度相同。

上述假设可杜绝机器人之间相向碰撞和追击碰撞问题，但无法避免交叉碰撞问题，具体可以分为两类：一是两台机器人将同时达到同一节点;二是一台机器人在某个节点转向时，另一台机器人即将到达该节点。要解决交叉碰撞可采用任一台机器人停止运动方式进行规避，对机器人设定优先级。本文根据机器人工作流程及模型构建要求，定义正在转向状态的机器人优先级最高，其次满载时的机器人优先级高于空载状态机器人，对相同负载状态机器人的优先级采用机器人编号的方式予以解决，即编号越小机器人优先级较高。最后，通过实时更新障碍物地图并将其结合预约表方法并结合传统A*算法以实现多机器人的动态路径规划。在机器人运行过程中，除了上货点和卸货点关键节点外，其余机器人所占据的节点作为障碍物添加到地图中。每台机器人只考虑下一步的动作和将要达到的节点，并将信息上传至控制中心，控制中心将这些信息整理后得到一张实时的障碍变化地图，各机器人再根据这张地图确定新的路径并将下一步的动作和将要达到的节点上传。如此往复可以实现多机协同的路径规划。

3  系统仿真验证分析（System simulation verification analysis）

本文主要基于NI myRIO实现智能仓储机器人实验平台，并在LabVIEW开发环境予以实现。

3.1   环境地图栅格化处理

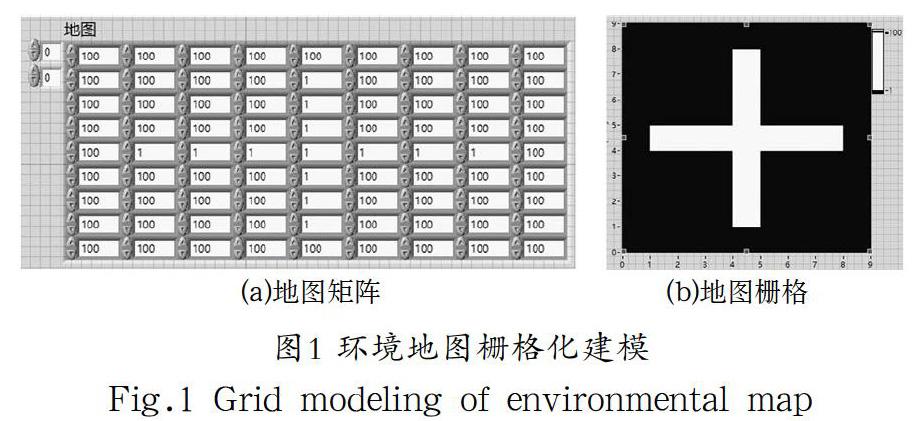
A*算法主要通过计算机器人通过某一位置时的代价函数来实现路径规划，本文在对仓储环境地图栅格化处理建模时，规定不可通行节点代价值为100，可通行节点代价值为1，以此构建一个地图矩阵，并采用LabVIEW强度图表进行显示，如图1所示。图中，黑色代表100，为不可通行的坐标，白色代表1，为可通行的坐标。

3.2   改进A*算法实验仿真

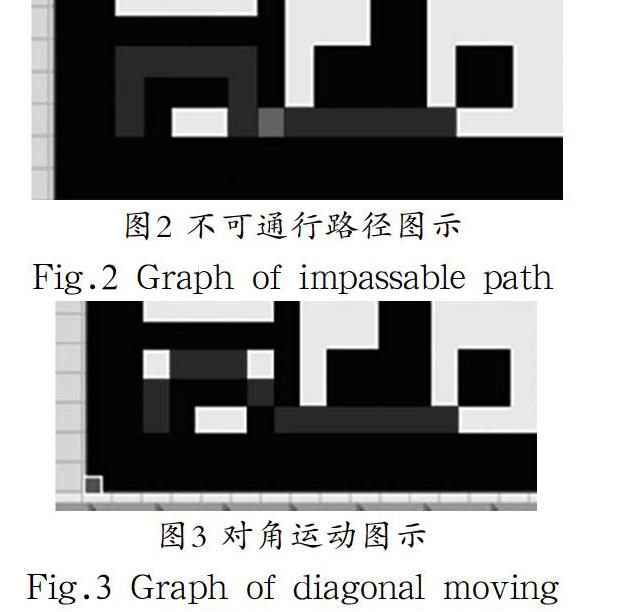
智能仓储机器人在运行过程中需完成障碍地图的更新、冲突坐标的调节，并基于各机器人当前坐标根据新的障碍地图重新规划路径。为减小仿真程序设计复杂性，每台机器人仅预测下一步节点坐标，主机根据所有机器人下一步节点坐标去协调可能有冲突机器人，以及更新障碍地图。传统A*算法是用来计算到达目标坐标的最佳路径，所以会规划出某些不可通行路径，如图2所示。

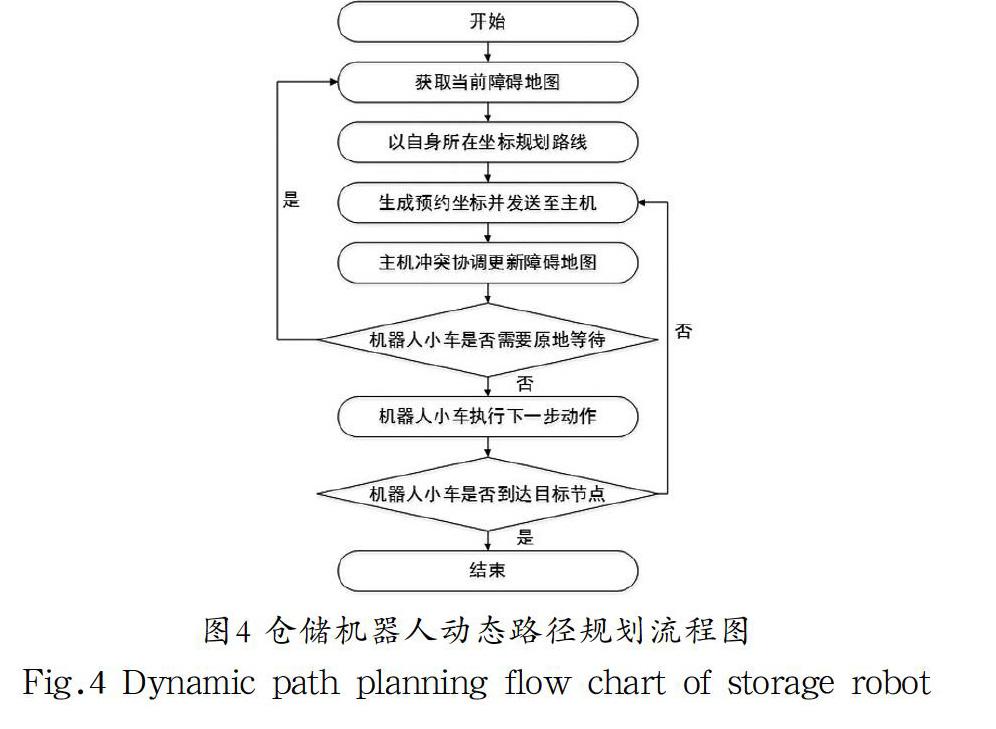
其中红色为不可通行节点。在实际应用中通常是不可能实现的，因此本文加入一个路径有效性验证程序，将障碍地图中不可通行的坐标数据进行处理，以验证路径中是不可通行坐标真实性。同时可判断出机器人的下一坐标是否为障碍坐标，进而判断出下一步的动作。在A*算法中，从某一个节点出发可有八种方向选择，如图3所示，但在仓储环境不允许机器人进行对角运动，可在A*算法中通过改变对角运动代价的方式来将该情况排除，对角运动和不可通行的节点一样，其代价设置为100。本文所提仓储机器人动态路径规划流程图如图4所示。

3.3   仓储机器人避障仿真模拟

图5为两台机器人发生交叉碰撞时仿真模拟，机器人1（蓝色）的优先级高于机器人2（红色）。机器人1由A向B运动，机器人2由C向D运动，图5（a）中两机器人的下一步均为节点E，发生交叉碰撞;主机根据优先级协调后机器人2原地等待，机器人1继续运动，如图5（b）所示;待机器人1通过节点E后，机器人2继续前进，如图5（c）所示;最终两机器人顺利通过节点E，如图5（d）所示。

3.4   仓储机器人路径规划代价分析

在路径规划中，如实际路线有不可通行节点，A*算法会优先走过可通行节点，而后再通过不可通行节点，故会出现图6所示往复行为。图6（a）中机器人1由E向B运动，会依次通过E→A→C→B;当机器人1刚到达节点A时，假设C处被机器人2占据，在下次的障碍地图更新后，C则为不可通行节点，A将会重新规划路线如图6（b），机器人1下一步将会回到节点E，当机器人2离开节点C时，机器人1又将重新回到节点A，出现往复的行为。为保证机器人不发生类似往复运动，可设定机器人节点与静态障碍物节点采用相同代价值，减少两条路径代价相同的情况，当有两条总代价花费相同的路径时，A*算法会优先选择第一个点代价更低的路径。

在实际应用中，当某一区域的机器人数量到达该区域的承受极限时，搬运机器人通过该区域的效率将会变得很低，影响仓储系统的整体效率。当某区域的机器人数量较多时，A*算法进行路径规划所求得通过该区域的路径代价将会更高，如果该代价大于两目标点间最大代价（两目标点曼哈顿距离与障碍物代价的乘积），则可能会规劃出穿过墙壁的错误路线，如图7所示。

机器人从A点运动至B的最优路径如图7（a）所示，当这条路径中有一台机器人停留时，假设所占据节点的代价为100，规划的路径如图7（b）所示，但当有两台机器人停留时，通过两台机器人路径的总代价大于从墙壁穿行的总代价，错误规划了一条不可通行路径，如图7（c）所示。可根据实际仓储环境和机器人数量合理设置该代价值予以解决。在上述环境中，两台机器人作为障碍物占据通行路径，设置代价为50，路径规划算法可正常工作，如图7（d）所示。

4   结论（Conclusion）

本文所提改进A*算法采用障碍地图和预约表相结合方法实现了智能仓储多机器人的动态路径规划和协同，通过实验仿真分析，可以看出所提方法可更好的利用仓库空间提高仓储效率。但仅对每个机器人下一步动作进行预约仍有很大局限性，无法满足大规模仓储环境应用，在实际应用中，可通过合理平衡场地大小与机器人实际运行数量两者之间的关系予以解决，保证系统可靠运行。

参考文献（References）

[1] 陈明智，钱同惠，张仕臻，等.仓储物流机器人集群避障及协同路径规划方法[J].现代电子技术，2019，42（22）：174-177;182.

[2]张国亮.动态环境中移动机器人路径规划研究综述[J].机床与液压，2013，41（01）：157-162.

[3] 李立，孙龙建.基于LabVIEW和NI myRIO的智能避障小车设计[J].电子器件，2018，41（02）：543-548.

[4] 董朝瑞，郭欣，李宁，等.基于改进A*算法的多机器人动态路径规划[J].高技术通讯，2020，30（01）：71-81.

[5] 王洪斌，尹鹏衡，郑维，等.基于改进的A*算法与动态窗口法的移动机器人路径规划[J].机器人，2020（03）：346-353.

[6] Karaboga D， Akay B. A comparative study of Artificial Bee Colony algorithm[J]. Applied Mathematics & Computation， 2009， 214（1）： 108-132.

[7] Ferguson D， Stentz A. Using interpolation to improve path planning：The Field D* algorithm[J]. Journal of Field Robotics， 2006， 23（2）： 79-101.

[8] 王勇.智能仓库系统多移动机器人路径规划研究[D].哈尔滨工业大学，2010.

[9] FazlollahtabarH， Saidi-Mehrabad M. Methodologies to Optimize Automated Guided Vehicle Scheduling and Routing Problems： A Review Study[J]. Journal of Intelligent & Robotic Systems， 2015， 77（3-4）： 525-545.

[10] 王志中.复杂动态环境下自主机器人路径规划研究[J].组合机床与自动化加工技术，2018（01）：64-68.

[11] Fu B， Chen L， Zhou Y T， et al. An improved A* algorithm for the industrial robot path planning with high success rate and short length[J]. Robotics and Autonomous Systems， 2018（106）： 26-37.

[12] 张丹露，孙小勇，傅顺，等.智能仓库中的多机器人协同路径规划方法[J].计算机集成制造系统，2018，24（02）：410-418.

[13] 张智，翁宗南，苏丽，等.室内机器人避碰路径规划[J].小型微型计算机系统，2019，40（10）：2077-2081.