EGM2008重力场模型在高程异常拟合中的应用
2020-07-27柯生学
柯生学
(中国电建集团西北勘测设计研究院有限公司,陕西 西安 710100)
0.引言
传统水准测量精度高,可靠性强,但往往耗费大量人力物力,测量速度慢,且受天气气候约束[1-4]。GNSS测量能在布网控制点上获得正高,但我国使用的是正常高系统(基于似大地水准面),为使测量结果能直接使用,必须计算高程异常值[5,6]。高程异常拟合需要获得测区一定数量的控制点坐标、大地高、正常高,若使用重力场模型还需要获得对应重力场模型计算的长波项,根据区域高程、高程异常值等条件选择适合本区域的拟合模型[7-10]。传统高程异常拟合模型受限于数学模型的特点,难以达到较高精度[11-13]。EGM2008 重力场模型作为美国发布的新一代重力场模型,可以精确计算待定点重力项高程异常,将之与移去-恢复法及常规数学模型结合,可以极大地提高高程异常拟合精度[14,15]。本文以西安某区域GNSS 水准数据为例,通过多项式拟合法、最小二乘配置拟合法、半参数模型结合移去-恢复讨论小区域高程异常拟合的最优模型[16,17]。
1.高程异常拟合的理论与方法
高程异常拟合有多种理论,本文主要采用以下三类:多项式拟合法、最小二乘配置法、半参数模型。
1.1 多项式拟合法
多项式拟合法是通过选取一定的拟合系数数量来控制模型起伏的一种数学模型,最少选择三个拟合系数,这时模型就是平面拟合模型。随着选择的拟合参数增加,模型起伏会有所变化,所需要的最少起算点也会随之增加。一般选择六参数多项式。拟合参数并非多多益善,因为拟合参数的增加会引起模型曲面的复杂起伏变化,有时反而会降低拟合精度。

多项式拟合模型可用式(1)表示:为高程异常;ε为残差;ai为待拟合参数;B,L为大地经纬度。误差方程式(2)为:

拟合系数矩阵

根据以上式可知多项式拟合至少需要六组已知点的高程异常及大地经纬度。将公共点数值带入上式,可得待估拟合参数X 计算公式(3)为:

1.2 最小二乘配置法
最小二乘配置法是一种优化模型,需要基于某个基础模型进行精度,一般优化六参数多项式。六参数多项式仅考虑到模型趋势项影响,未考虑非趋势项即随机误差的影响。最小二乘配置法将非趋势项作为优化目标,通过计算提高模型拟合精度。
最小二乘配置法可用公式(4)表示:

式中,L为已知点高程异常值,X为函数模型部分待拟合参数,B为函数模型部分系数矩阵;S为观测信号;Δ 为观测信号噪声。以S'表示未知点高程异常观测信号,式(5)可表示为:

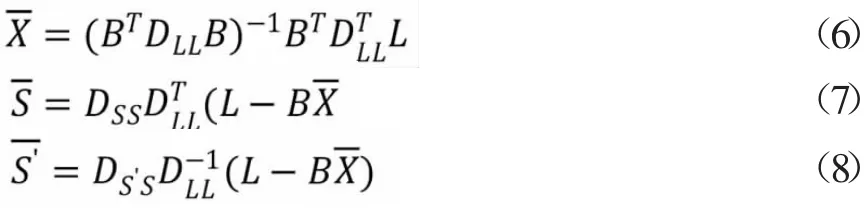
式中,DLL=DΔΔ+CDZZCT;未测点的最或然值见式(9):

1.3 半参数模型
半参数模型可用式(10)表示:

式中,L为已知点高程异常;B,X为参数模型函数系数矩阵与待估参数;S为半参数分量;Δ 为误差分量。误差方程见式(11):


式中,P为权阵(正定矩阵);α 为在极化过程中平衡V与S的纯量因子,称平滑因子;R为给定的正则化矩阵。由式(10)构造极值函数,可解参数分量与非参数分量
式中,N=BTPB;M=P+αR-PBN-1BTP。
依据最小距离法选取平滑因子α,αD为曲线上的点到原点距离最小时对应的α,当Sn2(αD) +Vn2(αD)=min时,α取得最优值,非参分量最优值经平差计算获得。利用式计算倾向参数Y,结合S计算出X,内插获得待算点的高程异常值见式(15):

2.高程异常拟合优化基于—EGM2008 的移去恢复
高程异常可分为以下几个部分:由重力场模型确定的中长波部分ξG、由Stokes理论确定的重力异常残余分量ξS、由地形改正得到的短波部分ξD。“移去-恢复”法的基本思想是:移去高程异常中的长波部分或者短波部分,然后将剩余部分结合拟合模型进行拟合计算,最后在待定点上恢复被移去的部分。由于缺少高分辨率的DTM数据,本文将短波部分与残余分量合并作为残差高程异常ξΔ=ξS+ξD。计算过程如下:
(1)根据GNSS 水准数据计算每点高程异常ξ';
(2)将ξ'与以EGM2008 模型计算的中长波部分ξG相减,得残差高程异常ξΔ;
(3)选择拟合模型对ξΔ进行拟合,确定最优待定参数,建立残差高程异常拟合模型;
(5)将外推所得ξΔ'恢复中长波部分,得该点高程异常拟合值
(6)对模型进行内外符合精度评定以及残差计算。
3.算例
3.1 工程概况
本文所用数据来自西安某区域,南北长约55 km,东西宽约30 km,地面标高为+35.38m~+36.29 m。矿区共有3 个C 级GNSS 点、19 个D 级GNSS 点和24 个E级GNSS 点,总计46 个GNSS 点都进行了相应等级的水准联测,矿区GNSS 点分布(如图1 所示)。
由图1 可知,已知点分布不均匀,因此以3 个C 级点做起算点,在矿区已有基础上,新增10 个GNSS 点进行D 级GNSS 测量,大地高与正常高观测结果(如表1 所示),由表可知所有点大地高变化不大,点位稳定可靠。
3.2 方案设计
根据测区概况,共设计六种计算方案,分别为:(1)六参数多项式;(2)六参数多项式+移去恢复;(3)最小二乘配置;(4)最小二乘配置+移去恢复;(5)半参数;(6)半参数+移去恢复。分别计算六种方案的拟合残差与内外符合精度进行对比。
3.3 实例计算与精度分析

图1 矿区已知点分布

图2 多项式残差对比

表1 GNSS 点可靠性分析

续:表1

图3 最小二乘配置残差对比

图4 半参数残差对比

表2 计算结果
六种方案计算结果见表1,其中MAX 表示残差最大值,MIN 表示残差最小值,RMSE 表示内/外符合精度结果。 残差对比(如图3、图4、图5 所示):由表2 可知,半参数+移去恢复方案内外符合精度均较小,分别为0.0038m 和0.0091m,六参数多项式模型内外符合精度较大,分别为0.0246m 和0.0311m;六参数多项式出现了最大内符合残差,为0.0695m,最小二乘配置法出现了最大外符合残差,为0.0650m,最小内外符合残差均出现在半参数模型,为-0.0618m 和-0.0688m。若不加入移去-恢复技术,半参数模型相对比其他两种模型并无明显拟合优势;最小二乘配置法相对六参数多项式的提升也比较有限。加入移去-恢复技术后半参数模型拟合精度提升比较明显,内外符合精度均在毫米级,可以很好地用于实际测量工作中。
4.结束语
通过三种方案计算表明,移去恢复技术可以有效地提高高程异常拟合精度,但在多项式与最小二乘配置中提升有限,在半参数模型中提升较为明显;半参数结合重力场模型的方案效果较好,最大内符合残差为0.0.471m,最大外符合残差为0.0153m,最小内符合残差为-0.0133m,最小外符合残差为-0.0078m,最适用于区域高程异常拟合。在实际应用中,若对高程异常求解要求精度不高,可直接采用多项式模型,其计算简单、不需要使用重力数据可以快速计算待定点概略高程异常;若需要高精度高程异常则需使用半参数+移去恢复的方法,以获得较好的拟合效果。
