海面短波地波正交频分复用自适应比特分配算法

杨蕾， 徐震， 张光普， 吴雷

(1.武汉轻工大学 电气与电子工程学院，湖北 武汉 430024； 2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001； 3.湖北电信工程有限公司，湖北 武汉 430000)

智慧海洋是信息与物理融合的海洋智能化技术革命4.0，是经略海洋的神经系统和海洋强国建设的长远战略抓手[1]。智慧海洋是国家海洋领域的一项重大创新工程，该工程以构建天、空、岸、海、潜信息一体化为目标，针对海上执法、环境监测、海上交通、海上应急等需求开展开发。为完善“智慧海洋”工程中，海面传输网络在传输层中的应用[2-8]，针对海面短波地波信道下的正交频分复用(orthogonal frequency-division multiplexing ，OFDM)通信系统，提出了一种改进自适应比特分配算法，该算法计算量较低，易于工程实现，且性能较好。

在OFDM通信系统中，自适应比特分配技术是其关键技术之一。现今应用较为广泛的自适应比特分配算法大多数为经典算法的改进算法。比较著名的自适应比特分配算法有贪婪算法[9]、Chow算法[10]、注水算法等。围绕这些经典算法进行的改进算法很多[11-12]，但是存在着共性问题，性能好的算法，复杂度较高；复杂度低的算法，性能较差。其中，简单分组比特分配算法是一种较其他自适应分配算法更为简化的比特分配算法。该算法以降低传输效率为代价，使复杂度大大降低，而更易于工程实现。改进算法基于经典SBLA算法对其进行改进，首先对原算法中用于计算信噪比的公式进行改造，使其更适用于海面短波地波信道，然后再用改造公式计算出来的信噪比指导比特分配情况，在不增加复杂度的基础上，尽可能提高系统传输性能。经计算机仿真得到的结果可知，改进算法性能较SBLA算法好，复杂度与SBLA算法接近。

1 海面短波地波OFDM系统模型

海面短波地波OFDM系统模型框图如图1所示。

图1 海面短波地波自适应OFDM系统Fig.1 The system chart of sea surface shortwave ground wave OFDM system

OFDM是一种较为特殊的多载波传输方案，兼并了调制技术与复用技术。OFDM系统相邻的子载波之间的频谱正交，使得接收端可以从各个子载波同时实现解调。运用OFDM系统，能够把一串高速串行数据分成多个并行低速数据流，并同时分别通过各个功率谱相互重叠的子载波进行传输，在接收端再进行逆操作，即可解调。为简化OFDM系统结构，可通过快速傅里叶变换FFT和逆快速傅里叶变换IFFT来模拟实现多个调制解调器的功能。OFDM技术具有很强的抗干扰能力，因其子载波之间的正交性将信道利用率大大提高了，故在海面短波地波通信中采用OFDM传输系统进行数据传输可保证数据传输速率需求。

为进一步提高系统性能和频谱利用率，将自适应比特分配技术引用入海面短波地波信道OFDM通信系统[12-13]。自适应比特分配技术是OFDM关键技术之一，该技术是一种非常灵活的自适应策略，采用这种技术可大大增加频谱利用率和系统性能。在目前的主流自适应算法中，大多数自适应算法虽然性能较好，但运算量巨大，工程实现困难[14]。简单分组比特分配算法(SBLA)因其运算过程主要用到加法或减法，故运算量较小，但性能较其他次最优经典算法差。改进算法对SBLA进行改进，将子载波进行编号选择使用，使其在保留运算量小的优点基础上提高性能。

SBLA算法是将子载波成组捆绑在一起，同一组子载波采用相同的调制方式，从而降低运算量的开销。该算法中子载波组的调制方式选取取决于信噪比，而信噪比的计算取决于信道情况。将海面短波地波信道特性引入到算法中，据此对信噪比计算公式进行改进，使信噪比计算更能真实反映信道情况。根据信道特性确定每组子载波的调制方式后，再分别对各组子载波分别编号，每一组只使用部分子载波进行数据传输，从而提高系统性能。

2 海面短波地波信道

短波信道是时变衰落信道，但在有限带宽、传输时间不长的情况下，其信道特性基本上是稳定的，可以用一个适当的信道模型来表示。Watterson 等[]提出的一种窄带短波信道模型，该模型是国际无线电咨询委员会(CCIR)推荐的短波信道模型之一。许多学者以Watterson信道模型为结构基础，通过对其模型的理论和结构加以扩展和补充，提出了许多根据不同工程和应用需要而改进的其他Watterson 信道模型。

在地面上进行的短波地波通信主要受电台干扰、大气噪声、宇宙噪声、工业噪声等噪声的影响，但就智慧海洋中海面短波地波通信而言，电台干扰、宇宙噪声跟工业噪声可以忽略不计，故海面短波地波信道的主要研究内容在于描述大气噪声的干扰。

因对于通过海面短波地波信道进行传输的数据来说，接收端接收到的信号主要由直达波和海面反射散射波组成，故在海面短波地波信道模型中主要考虑的是多径时延。

基于Watterson信道模型来构造海面短波地波信道，可得到海面短波地波Watterson信道的冲击响应为：

(1)

式中：L为路径数；fdk为多普勒频移；φk为初始相位；τk为时延。

3 改进自适应比特分配算法

经典的SBLA根据每组子载波的平均信噪比来确定采用何种调制方式，因此，信噪比的计算和门限取值是关键问题。该算法中，信噪比门限的绝对值是可变的，但是各门限之间的间隔不变，是由各种调制方式的BER曲线在10-3处的值得到的。可见，这种算法主要用到加法或减法运算，所以计算复杂度很低[11]。下面基于SBLA算法对改进算法进行描述。

1)自适应调制OFDM系统数学模型。

首先给出自适应调制的OFDM系统数学模型。对于SISO OFDM系统来说，自适应调制的基本思想是利用信道特性自适应调节数据信息，并进行传输。设总子载波数为N，无干扰OFDM系统子载波幅值为Aj，j=0,1,…,N-1，则接收端子载波信号可表示为：

Yj=HjAjXj+Wj

(2)

式中：j=0,1,…,N-1，Hj为子载波频率响应；Xj为子载波发送信号；Wj为复加性高斯白噪声。若hl为多径信道抽头因子，l=0,1,…,L-1，L为多径信道路径数，则：

(3)

系统的信噪比为：

(4)

(5)

在实际应用中，Hj服从瑞利分布，且各子载波频响相互独立，子载波间的衰落强度相差较大，故OFDM系统传输性能主要取决于Hj中衰落最严重的子载波。

2)改进算法原理。

改进算法所采用的优化原则并不是信道容量优化原则，而是误码率最小原则。误码率最小原则是已经被应用，且被证实有效的优化原则之一。改进算法流程如图2所示。

图2 改进算法流程Fig.2 The flow chart of this improved algorithm

为得到各组子载波上比特分配的依据，首先需要计算各组子载波的信噪比。设总子载波数为N，将N个子载波平分为NB组，则每组子载波数为n=N/NB，i=1,2,…,NB。原算法中计算各组子载波的信噪比利用的是信道响应，即，SNRi=|hi|2,i=1,2,…,NB。现将信噪比计算公式进行改进，从而进一步提高误码性能。具体步骤如下所述。

首先，经海面短波地波信道传输后，接收端接收到的信号信噪比应被表示为接收信号场强与大气噪声之比。由上面假设可知，信道被划分为NB组，则信噪比应被表示为SNRi=SNRGi|hi|2，i=1,2,…,NB，其中SNRGi为第i组接收信号信噪比。考虑海面短波地波特性，SNRGi应为：

SNRGi=E/En

(6)

式中：E为距离辐射源r处的电场强度，En为大气噪声场强。

设发射天线的辐射功率为P，天线的方向性系数为D，则距离辐射源r处的电场强度为：

(7)

海面短波地波信道存在严重的衰减问题，在计算电场强度时应将此因素考虑进去。设海面衰减特性损耗电阻为Rt，由实际地面损耗电阻经验公式有：

Rt=Aλ/4h

(8)

式中：A为与地质有关的常数，约等于2～7，λ为传输的电磁波波长，h为天线高度。λ/h的值越大，损耗越大，效率降低。故考虑了海面地波衰减的场强公式应表示为与天线效率相关。

天线效率为：

(9)

另外，在海面短波地波信道中，存在的外部噪声中大气噪声贡献最大，此处忽略其他噪声影响，令大气噪声场强表示外部噪声影响。由CCIR-322报告可知，大气无线电噪声场强有效值为[15-16]：

En=Fa+10logB+20logf-96.8 (dB.μV m)

(10)

式中：Fa为大气无线电有效噪声系数，可用来计算Fa=Pn/KT0B；Pn为无方向性短垂直天线接收到的噪声功率；K=1.38×10-23为玻尔兹曼常数；T0=288 K为参考温度；B为接收机有效噪声带宽；f为接收机工作频率。

综上所述，在考虑了地表面衰减、发射天线效率以及大气噪声场强的情况下，接收点处的信噪比应为：

SNRGi=E+ηA-En

(11)

基于上述论证、推导，可得海面短波地波第i组信道的信噪比为：

SNRi=(E+ηA-En)|hi|2

(12)

计算出各组信噪比后，可得全部子载波的平均信噪比：

(13)

设置目标深度Rtarget，初始可将其设定为每个子载波固定分配2 bit，则Rtarget=2N。根据上式计算出来的SNRmean和Rtarget，可计算得到平移SNR门限：

SNRstd=SNRstd+SNRmean-SNR(Rtarget+1)

(14)

由式(14)可确定SNRstd和各组子载波的，再由SNRi与表1数据可得到每组子载波应分配的比特数。设第i组各子载波上分配的比特数为Ri，利用式(14)所确定的SNRstd与各组子载波的SNRi，可得：

ΔSNRi=SNRi-SNRstd(Ri)

(15)

(16)

表1 不同调制方案的SNR门限(BER=10-3)

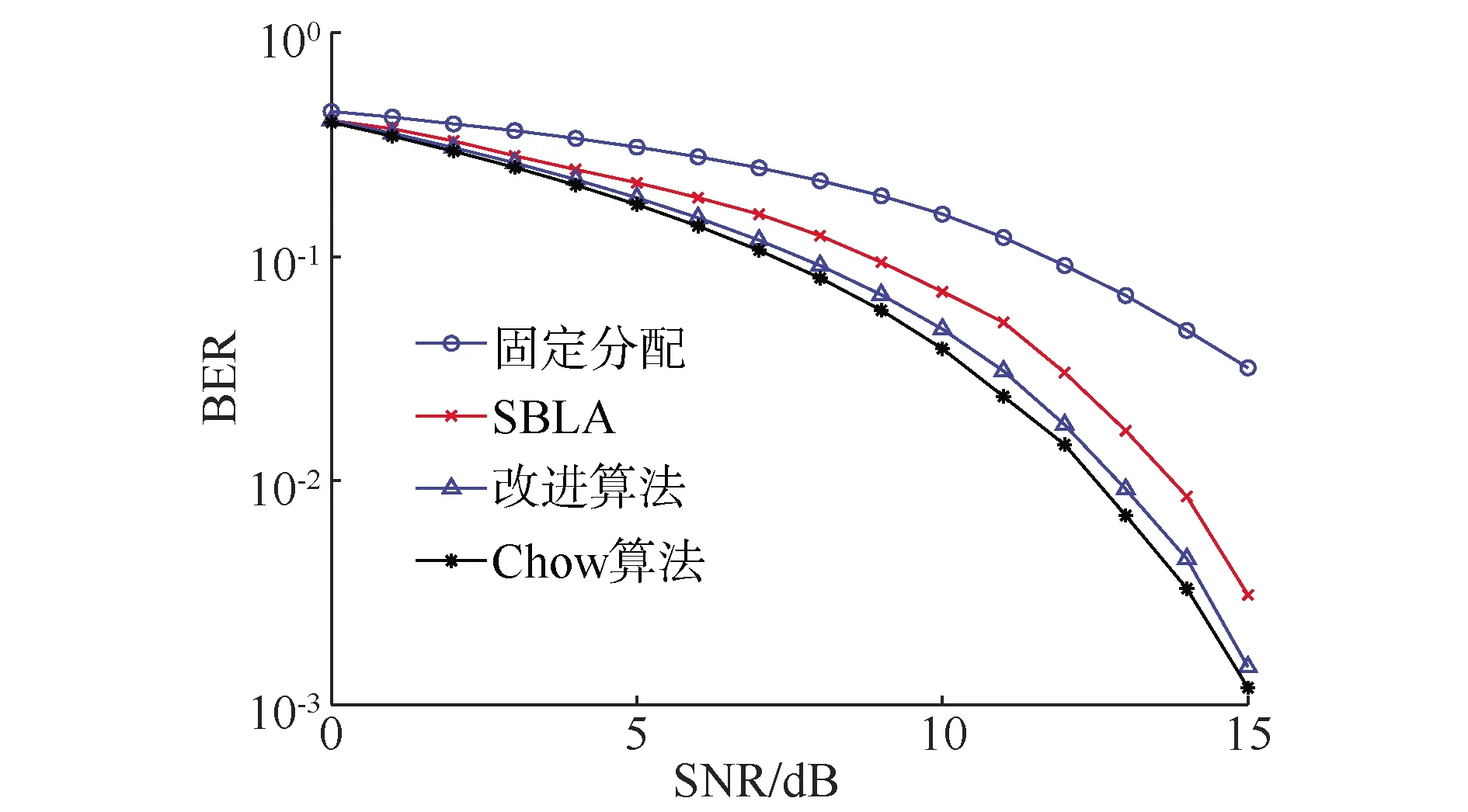
比较Rsum和Rtarget，若Rsum=Rtarget，则比特分配结束，否则调整Ri直到Rsum=Rtarget为止。若Rsum>Rtarget，则查看NB个ΔSNRi值中的最小值，并找出有比特分配的最小ΔSNRi载波组，调整该组的比特分配值，令这一组的比特数减1，即Ri=Ri-1，则总比特数Rsum也将随之减少1。将对应的ΔSNRi增加1，即ΔSNRi=ΔSNRi+1。反之，若Rsum

信噪比公式改进完毕后，再对子载波做随机选用处理。前面已假设第i组子载波分配比特数为Ri，i=1,2,…,NB，因N个子载波被平均分为NB组，每组子载波数为n。这n个子载波并不会全部用来承载数据，而是从这n个子载波中取k个来承载数据，可将其称为“可用子载波”，而不承载数据的子载波可称其为“无用子载波”。因每组子载波分配比特数为Ri，故将这Ri个比特拆分为p1比特和p2比特，即Ri=p1+p2。其中p1比特用于从该组n个子载波中挑选出k个有用子载波，p2比特首先进行星座点映射，然后将映射好的星座点频域数据调制到由p1比特挑选出的k个有用子载波上，从而完成该组子载波的信息比特调制工作。k个有用子载波的选择方式可参见表2。假定系统参数为n=8，k=3，那么从8个子载波里选出3个有用子载波会有C(8,3)=56种可能的模式，又因为p1取值必须取整，有p1=[lb56]=5，故p1只能取5。表2中给出了任意选取的8种可能发送模式。确定了p1的模式后，再将有用子载波组合与之一一对应，如表2第2列所示。最后再将前面利用p2比特映射好的星座点调制到所选出的有用子载波上，如表2第3列所示，至此，则完成了第i组子载波的调制。

之后，将整个NB组信息进行IFFT变换，并按照传统OFDM通信系统的处理方式加循环前缀，而后进行发送。表2信息将被传递到接收端，在接收端可利用该表信息进行解调。

表2 n=8，k=3时的发送模式表格Table 2 Table of sending mode with n=8,k=3

改进算法中，将子载波进行编号处理，并选择性使用，使得只有部分子载波参与调制传输，从而可在一定程度上提高系统误码性能。同时，在选择有用子载波进行信息传输时，有用子载波是随机选取的，子载波标号本身会携带一定信息，因此在信息传输方面并没有太多损失。

4 计算机仿真

分别对AWGN信道和海面短波地波信道下的传统固定分配OFDM、采用SBLA算法OFDM、采用改进SBLA算法OFDM和采用Chow算法OFDM的4种情况，进行了计算机仿真。系统参数如下所述。

信噪比取0～15 dB，海面短波地波信道为三径信道，第1条路径相对时延设定为0 ms，衰减系数为1；第2条路径相对时延设定为2.5 ms, 衰减系数为0.3；第3条路径相对时延设定为5 ms, 衰减系数为0.1；最大多普勒频移为0.1 Hz。假设此OFDM系统采用802.11a系统物理层参数，其中，系统子载波数为64，循环前缀长度为16。

性能仿真图如图3、图4所示。仿真结果表明，在AWGN信道下，采用自适应算法的OFDM系统性能远远优于传统OFDM；3种自适应算法比较，Chow算法优于SBLA算法和改进SBLA算法。改进SBLA算法性能接近于Chow算法且优于经典SBLA算法。

图3 传统固定分配OFDM与3种自适应分配OFDM性能比较图(AWGN信道)Fig.3 The performance comparison of fixed OFDM and three adaptive OFDM (AWGN Channel)

图4 传统固定分配OFDM与3种自适应分配OFDM性能比较图(海面短波地波信道)Fig.4 The performance comparison of fixed OFDM and three adaptive OFDM(Sea surface shortwave ground wave)

在海面短波地波信道下，采用自适应算法的OFDM系统性能同样也是明显优于传统OFDM；3种自适应算法比较结果与AWGN信道结果相同，Chow算法性能最优，改进算法次之，优于SBLA算法。

综上所述，在不同信道情况下，性能上，改进算法误比特性能好于经典SBLA算法，略差于Chow算法；计算量上，改进算法要远远低于Chow算法。显然，改进算法在工程实现上更具有实际意义。

5 结论

1)文中针对海面短波地波通信，提出了改进OFDM自适应分配算法，该算法依据海面短波地波信道特性使用改进信噪比计算公式计算每组子载波信噪比，又通过筛选分组比特来进一步提高误码性能。

2)计算机仿真结果验证了该算法的正确性和可行性。结果表明，改进算法克服了传统经典算法的复杂性问题，而其性能并未受到太多影响。

3)本文提出的海面短波地波OFDM自适应分配算法对完善海面短波传输网络在“智慧海洋”工程传输层中的应用提供了一种研究方案。