基于围岩变形的预应力锚杆受力特征分析及锚固机理

2020-07-27赵呈星李英明

煤矿安全 2020年7期

赵呈星，李英明

（1.安徽理工大学能源与安全学院，安徽淮南232001；2.煤矿安全高效开采省部共建教育部重点实验室，安徽淮南232001）

锚杆、锚索加固支护技术在水利工程、土木工程、岩土工程、采矿工程已广泛应用，大量的工程实践也推动了锚固技术发展，并认识到采矿工程中预应力锚杆对煤矿巷道围岩控制起决定性作用[1-4]。随着我国煤矿采深及强度的增加[5]，巷道围岩节理裂隙发育、松软破碎、破坏范围大，预应力锚杆承载能力需不断增强，因此研究预应力锚杆在实际支护过程中与围岩相互作用力学机制及预应力锚杆杆体应力分布特征是围岩控制技术中重要内容。

国内外学者通过理论分析[6-9]对预应力锚杆锚固机理及应力分布特征展开了大量的研究工作。文献[10]在不同锚固长度条件下建立力学模型分析探讨了预应力锚杆对围岩的控制效果，认为留设一定长度的自由段有助于锚杆预紧力在围岩中的扩散，当锚杆间排距较大时，增大预紧力、减小锚固段长度可提升锚杆锚固性能；文献[11]研究了圆形托盘对预应力锚杆应力场分布的影响；文献[12-14]通过数值模拟及工程实践经验研究了预应力锚杆的作用机理及锚固效果，并探讨了相关因素对预应力锚杆支护的影响；文献[15]在考虑围岩离层影响的条件下通过理论分析得出预应力锚杆锚固段轴力和剪应力均会增大的结论。而在巷道开挖后，由于围岩初始地应力场破坏，靠近巷道表面内围岩开始进入塑性破坏状态形成围岩破碎区，预应力锚杆实际支护时正是对支护范围内的围岩产生径向约束，控制破碎区的再次扩大，所以分析预应力锚杆应力分布规律应当考虑围岩的实际变形。因此，在已有的研究基础上，建立了预应力锚杆－围岩相互作用模型，在考虑围岩实际变形及锚固体滑移的情况下分析了锚杆自由段及锚固段受力状态，得到了预应力锚杆自由段及锚固段应力分布计算解析式，进而获得自由段、锚固段应力分布规律，为锚固支护设计提供一定的理论基础。

1 预应力锚杆－围岩支护模型

预应力锚杆受力不仅与锚固系统材料、尺寸、屈服强度、预紧力大小等有关，围岩强度、节理裂隙分布、围岩应力等对锚固系统支护强度同样有显著影响。巷道的开挖，使得原本处于平衡的围岩应力重新分布，浅部围岩应力由三向变为两向，造成围岩塑性区内出现破碎区。而预应力锚杆能对围岩进行有效支护主要因为其锚固部分有效控制了围岩破碎区范围的扩大，因此假定锚杆在塑性区内破碎区外，建立的预应力锚杆－围岩支护力学模型如图1。

锚杆分为自由段与锚固段，杆体长度为L，自由段长度L1，锚固段长度L2，p0为围岩应力，F 为人为施加的预紧力。

2 预应力锚杆受力分析

2.1 锚杆自由段受力分析

从建立的力学模型可看出预紧力和围岩变形是影响锚杆受力的主要因素，而预应力锚杆对围岩进行有效支护时，杆体分为自由段和锚固段2 部分，且锚固长度不大于锚杆长度的1/3[16]。由于锚杆自由段位于围岩破碎区且与围岩之间无锚固剂，所以预紧力是影响锚杆自由段轴力的主要因素。

图1 预应力锚杆－围岩支护力学模型Fig.1 Supporting mechanics model of pre-stressed bolt and surrounding rock

由弹性理论，锚杆自由段沿其轴向的刚度C为：

式中：As为锚杆横截面面积；Es为锚杆弹性模量；L 为杆体长度。

所以，可得到锚杆自由段轴力N1为：

式中：△L 为锚杆自由段在外荷载作用下轴向变形量。

△L 由自由段两端围岩变形确定，则有：

式中：U0为巷道围岩表面位移；U1为锚杆自由段末端处岩体径向位移。

2.2 锚杆锚固段受力分析

锚杆锚固段位于围岩塑性区内，杆体与围岩通过锚固剂黏结。锚固剂一般为水泥浆、树脂等，与杆体形成锚固体控制围岩破碎区，而锚杆锚固段受力包括预紧力作用下的受力及围岩变形引起的受力2部分。据此，对锚杆锚固段单元受力分析，锚固段单元受力分析示意图如图2。

建立平衡微分方程有：

式中：N2为锚固段微元所受轴力；r 为锚固段横截面半径；τ（x）为锚固段微元所受剪应力；x 为x 点。

预应力锚杆在实际支护过程中大致分为2 个阶段：初始阶段与围岩塑性区耦合良好，能有效控制围岩破碎区的扩大，而随着围岩变形量的增加，出现锚固体与围岩解耦，之间产生相对滑移。按照折线剪切滑移模型[17]计算，有：

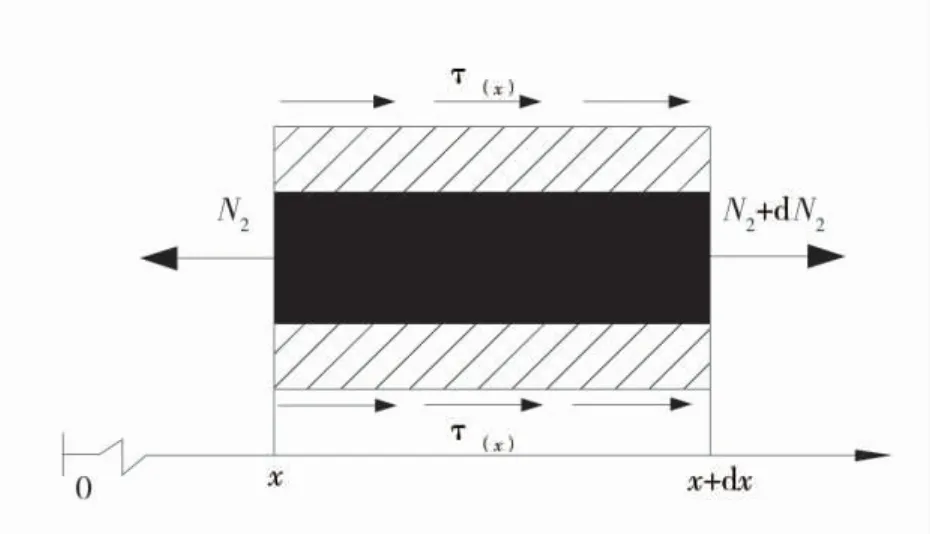
图2 锚固段单元受力分析示意图Fig.2 Schematic diagram of force analysis of anchorage unit

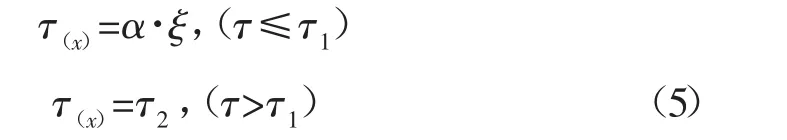
式中：ξ 为锚固体与围岩之间的相对位移；τ1为锚固界面临界剪切刚度，由摩尔库伦屈服准则确定；τ2为滑移剪切度；α 为界面剪切刚度系数，其表示单位剪切位移所产生的剪应力，一般由剪切实验确定。

式中：α1为岩体剪切刚度，硬岩取5～10 GPa，软岩取1.5～3 GPa，风化岩取1～2 GPa，泥岩取1.2～2.5 GPa[18]；α2为锚固体综合剪切刚度。

有以下关系式成立[19]：

式中：Gs为锚固剂的剪切模量；r1为锚杆横截面半径。

在预应力锚杆支护初期，围岩与锚固体充分耦合。在此阶段，预紧力是引起锚固体变形受力的主要因素，现假设x 点处锚固体轴向位移为Us（x），由式（5）可得：

将式（8）代入式（4）有：

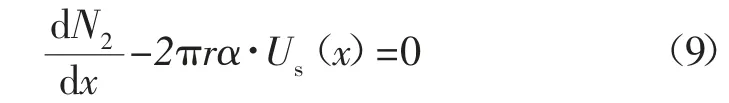
并对上式求导可得：

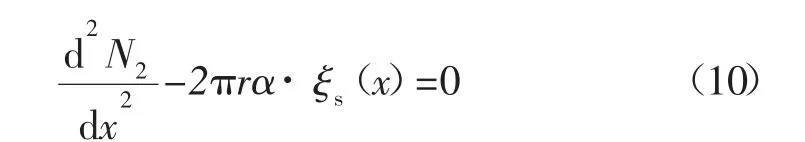
式中：ξs（x）为锚固段轴向应变。

由虎克定律可知：

式中：Ab为锚固体折算横截面面积；Eb为锚固体折算弹性模量。

Ab表达式如下：

式中：Ac为锚固剂横截面面积；Ec为锚固剂弹性模量。

由式（10）、式（11）可得：

其中，

式（20）属于二阶常系数非齐次微分方程，可求得其解为：

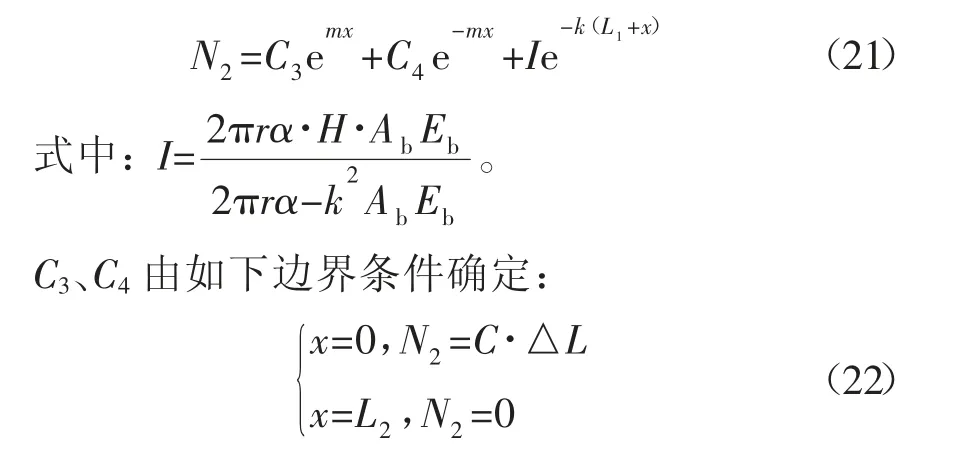
可得，在围岩变形条件下锚固段所受轴力及剪应力：

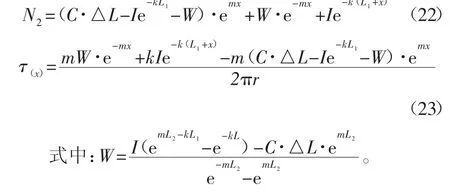
将围岩变形量及锚固参数分别代入在预紧力作用下及围岩变形条件下预应力锚杆的轴力、剪应力解析式并进行叠加可得到其自由段及锚固段应力分布。而对于锚杆锚固段应力分布计算，先假定锚固体与破碎区围岩黏结良好，将上述2 种条件下锚固段轴力及剪应力叠加，然后将各分段叠加后的剪应力与锚固界面临界剪切刚度比较，若超过，则表示该分段剪应力值为滑移剪切度，处于滑移状态。滑移段轴力可对式（4）积分计算：

式中：ω 为积分常量，由锚固体滑移段端部轴力确定。

ω 值确定之后，令x=0，便可对整个自由段轴力修正。

3 算例分析

假设巷道埋深350 m，半径为4 m，围岩为软岩，其黏聚力为0.8 MPa，内摩擦角30°，塑性区半径7 m，锚杆弹性模量200 GPa，直径16 mm，长度2.5 m，锚固长度0.6 m，锚固剂直径23 mm，弹性模量为18 GPa，剪切模量为36 MPa，施加预紧力为25 kN，按上述步骤计算可得到预应力锚杆轴力及剪应力分布曲线，预应力锚杆应力分布曲线如图3。

从图3（a）可看出，锚杆自由段部分由于锚杆杆体与围岩未接触导致所受剪应力为0，在距孔口1.9 m 处锚固界面剪应力急剧增大至1.36 MPa，而锚固界面临界剪切度按摩尔库伦准则计算为2.34 MPa，锚固段未发生滑移，所以剪应力达到峰值后沿锚杆长度方向快速衰减至0。从图3（b）可看出，在围岩变形及预紧力施加的影响下，孔口位置处锚杆轴力达到峰值为66.44 kN，且在锚杆自由段内保持不变，在锚固段端部所受轴力沿锚杆长度方向下降并于锚固段尾部减小为0。