伸缩因子驱动的曲线自由变形设计方法

李运平 高直

摘 要：为简化伸缩变形计算过程，针对代数曲线和参数曲线，提出一种具有区域峰值的伸缩因子曲线变形方法。首先基于Hermite插值基函数构造一种多项式伸缩函数，然后建立带有伸缩参数的伸缩因子，最后将伸缩因子作用于曲线，促使曲线沿指定方向产生变形。在变形过程中，通过改变伸缩因子中的形状控制参数，实现曲线整体、局部以及周期变形效果。大量数值实例证明，该方法计算量小，便于理解和操作，可获得适用于不同设计要求的旋转曲面和外形轮廓线。与其它方法相比，该方法不仅可用于参数型曲线，还可用于隐式表示的代数曲线，丰富了隐式曲线的变形效果。

关键词：自由变形;代数曲线;参数曲线;伸缩因子

DOI：10. 11907/rjdk. 192404 开放科学（资源服务）标识码（OSID）：

中图分类号：TP319文献标识码：A 文章编号：1672-7800（2020）007-0108-04

Free Form Deformation Design of Curve Driven by Expansion Factor

LI Yun-ping， GAO Zhi

（School of Information Engineering， Yancheng Institute of Technology， Yancheng 224051， China）

Abstract： In order to simplify the deformation calculation process， a curve deformation method with regional peak expansion factor is proposed for the algebraic curve and parameter curve. First， a polynomial expansion function is constructed based on the Hermite interpolation basis function. Then the expansion factor with the expansion parameters is established. Finally， the deformation of curve is calculated by the expansion factor. In the deformation process， by changing the different shape control parameters of the expansion factor， the global， local and periodic deformation effects of the curve can be achieved. Examples show that the calculation of the method is small， easy to understand and operate. This method can obtain the rotating curved surface and contour for different design requirements. Compared with other methods， this method can not only be applied to parametric curves， but also implicit representation of algebraic curves. This method enriches the deformation effect of implicit curves.

Key Words： freeform deformation; algebraic curve; parametric curve;extension factor

0 引言

计算机动画、产品设计和大数据可视化等领域经常对已有几何图形进行编辑使其形状适用于新的需求。在编辑过程中，初始几何图形与新造型之间的映射关系称为变形。1984年，Barr[1]率先将变形方法引入到几何造型领域;Sederberg等[2]提出了自由变形（FFD Freeform Deformation）法，借助三变量张量积Bézier体控制网格顶点对嵌入的图形进行变形控制。FFD方法是一种独立于模型几何表示的变形方法，但交互过程繁琐、计算量大且难以精确控制变形结果。在上述算法基础上，研究出大量算法解决曲线的变形与修改问题。Piegl[3]、Au等[4]分別提出了有理 B 样条和 NURBS 曲线局部形状修改方法，但是形象直观性不足，难以进行交互操作;Sánches-Reyes[5]给出了基于任意原点透视变换的NURBS 曲线形状修改方法;蒋大为[6]提出并验证了有理 Bézier 曲线的权因子修改方法;闫艳等[7]分别通过修改单个权因子、单个控制点、同时修改单个权因子和控制点等方法，对NURBS曲线进行形状修改，通过修改多个权因子、多个控制点来修改曲线形状，并给出相关公式;张世杰等[8]提出基于渐进迭代逼近与主顶点方法的曲线局部变形方法。上述变形算法属于几何变形方法。为进一步模拟物体的真实变形结果，关志东等 [9-10]将有限元方法引入到曲线曲面变形中，通过构建有限元网格以及添加几何约束得到变形结果;王青等[11]通过曲线控制网格，类比为空间索网结构，分别建立外载荷变化最小、外载荷最小、杆阻尼长度最小和节点位移最小等4种表达不同几何和物理意义的最小化模型来驱动变形;程仙国等 [12]运用力学思想构建曲线在载荷作用下的变形能量方程，以驱动B样条曲线变形;文献[9-12]属于物理变形方法，变形结果真实，但涉及较深的物理理论知识和复杂的方程求解。

为简化变形步骤，便于交互控制曲线形状，基于伸缩因子的曲线变形技术得到广泛关注。王小平等[13-14]基于指数函数类和余弦函数类等超越函数构造伸缩因子，将伸缩因子作用于参数曲线曲面进行变形。该方法简单易操控，但仅具有单点峰值，且变形后曲线表达式为超越曲线;宋来忠等[15]通过对指数函数进行积分构造伸缩因子，能够达到区间峰值，但变形后仍为超越曲线;陆友太等[16-17]构造了区域上达到峰值的多项式伸缩因子;张莉等[18]提出了一种新的带平台多项式伸缩函数，可用于产生富含角点或尖点的目标参数曲线曲面;在此基础上，陈素根[19]提出了参数曲面上任意凸多边形区域的伸缩变形算法，扩展了已有的参数曲面伸缩变形技术。上述伸缩变形方法的研究对象为参数曲线曲面。针对代数曲线曲面的伸缩变形，李军成等[20]基于余弦函数提出了适用于代数曲线曲面变形的伸缩因子，该方法计算简单易控制，但是缺少区域峰值特性，在支撑区间长度過大时会产生多峰现象。

本文针对代数曲线和参数曲线，提出一种基于Hermite插值基函数的伸缩因子，它不仅能在单点处达到峰值，在区域上也能达到峰值，而且适用于曲线不同的表达方式。在产品设计中运用文中的伸缩因子首先对曲线进行变形，进而可采用绕轴旋转的方式产生形状丰富的旋转体模型。

1 伸缩函数与伸缩因子

1.1 伸缩函数

定义1设 [m，n∈R]，称分段函数

为定义在R区间[[x1，x4]]上的伸缩函数。其中[[x1，x4]]为支撑区间，[x2，x3]是支撑区间上的任意两点。

依据Hermite插值基函数特性，所提出的伸缩函数[f（x）]具有如下性质：

（2）区间峰值性和单峰性：当[x∈[x2，x3]]时，函数在此区间上取最大值1，如图1（a）所示;当[x2=x3]时，函数在单点取最大值1，如图1（b）所示。

（3）端点连续性：

1.2 伸缩因子

定义2：设[h∈R]，称函数

为在[[x1，x4]]上的伸缩因子，h为伸缩参数。

由伸缩函数性质得出伸缩因子具备以下性质：

（1）区间峰值性和单峰性：[x∈[x2，x3]]函数在此区间上取最大值h;当[x2=x3]时，函数在单点取最大值h。

（2）端点连续性：

通过调整伸缩因子中的参数数值和支撑区间，可得到不同表现形式的伸缩因子。图2展示了当伸缩参数符号相反时，伸缩因子的数值变化结果。同时，通过控制变形区间可使伸缩因子达到区间峰值和单点峰值效果。

2 代数曲线伸缩变形计算与实例分析

2.1 简单变形计算

设[（x，y）T]为平面代数曲线[l]上的点，将式（1）中定义的伸缩因子作用于曲线方程，得到变形后的点[x*，y*T]，其计算公式如下：

其中，[d=（dx，dy）T]为伸缩方向单位向量。一般情况下，伸缩方向可沿y轴正向伸缩和沿曲线法线方向伸缩。

沿y轴正向伸缩则[d=（0，1）T]，变形后的点[（x*，y*）T]为：

沿曲线法线方向伸缩，记[d=（nx，ny）T]为曲线[l]在[（x0，y0）]处的法向量[（F′x（x0，y0），F′y（x0，y0））T]的单位化向量，其中[F（x，y）]为曲线[l]的隐式表达式。变形后曲线的点[（x*，y*）T]为：

根据伸缩因子端点连续性可知，变形后的曲线[l*]在端点[x1，x4]处连续。同时，[l*]是[l]在支撑区间上产生变形的结果。当支撑区间[[x1，x4]？[a，b]]时，[l]仅发生局部变形;当支撑区间[[x1，x4]？[a，b]]时，[l]将发生整体变形。

2.2 周期变形计算

为丰富曲线的变形形状，对曲线进行周期变形计算。记待变形曲线的变形区间为[[a，b]]，变形周期数为[ω]，则变形周期为[d=b-aω]，每个周期的支撑区间表示为[[xi1，xi4]，][i=1，2，？ω]，其中[xi1=a+（i-1）d]，[xi4=a+id]。若伸缩函数的分段区间均匀分布，可取[xi2=xi1+d3]，[xi3=xi1+2d3]。在每个周期按照式（1）定义伸缩因子进行变形计算。

2.3 变形控制方法

通过调整伸缩公式（2）中的各个参数值可获得不同的变形效果：① 改变伸缩参数h的大小和符号，用于调整伸缩变形幅度和变形方向;② 改变支撑区间[[x1，x4]]，调节待变形曲线的变形区域，以实现整体和局部变形;③ 参数m， n用于调节曲线的光滑程度，m， n值越大，变形后曲线在端点[x1，x4]处越逼近初始曲线;④峰值区间长度依赖[x2，x3]的取值，当 [x2=x3]时，变形曲线峰值点在[x2]处;⑤ 伸缩方向向量[d=（dx，dy）T]的取值决定曲线变形方向，方便曲线按照用户给出的方向进行变形。

2.4 实例分析

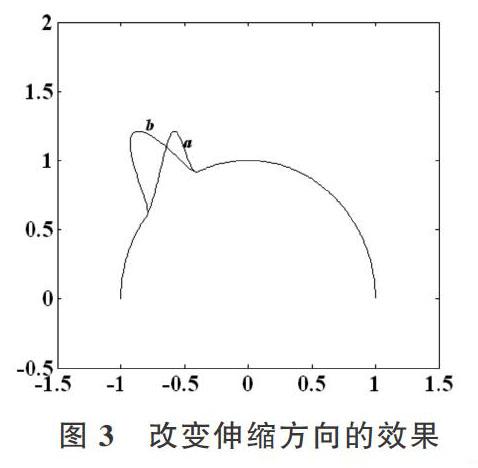
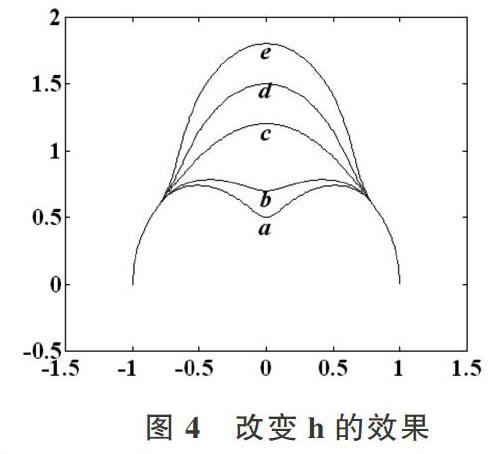
以单位圆[x2+y2=1]及其上半圆弧为例，通过改变变形控制参数获得各种变形结果。图3给出了伸缩方向向量的改变对变形结果的影响，其中曲线a的伸缩方向向量[d=（0，1）T]即y轴正向，曲线b的伸缩方向向量[d=（nx，ny）T]即圆弧上点的法矢方向。图4为改变伸缩参数h 的变形效果。曲线a-e所对应的伸缩参数h分别为-0.5、-0.3、0.2、0.5、0.8。

图5展示了支撑区间的改变对变形结果的影响，曲线a-c所对应的支撑区间如表1所示。通过调整支撑区间的参数值可实现曲线的区域峰值、单点峰值效果。

图6通过调节参数m、n的值改变曲线在端点[x1]和[x4]处的光滑度，其中曲线a中m=n=1;曲线b中m=4，n=2。

图7展示了圆弧沿法矢方向的周期变形效果。将区间[-1，1]十等分，以每个等分区间作为支持区间，根据式（2）计算变形结果。由图7可以看出，在支撑区间长度相同的条件下，两端支撑区间所对应的弧较长，而中间弧长相对较短，弧长长度随着区间均匀变化，这主要是由于圆弧所采用的隐式方程表示所致。

图8展示了直线周期变形效果。伸缩参数h按照周期的顺序依次递增。图9为直线在伸缩因子的作用下产生曲线，通过绕坐标轴旋转的方式构造旋转曲面。图9（a）为通过区域峰值伸缩因子构造的旋转曲面，图9（b）为通过单峰值伸缩因子构造的旋转曲面。

3 参数曲线伸缩变形计算与实例分析

3.1 参数曲线伸缩变形计算

设平面参数曲线[l（t）=（x（t），y（t））T] [t∈[a，b]]，类似于代数曲线，将式（1）中定义的伸缩因子作用于曲线得到变形后曲线[l*]上的点[x*，y*T]为：

其中，[d=（dxt，dyt）T]为伸缩方向单位向量。参数曲线周期变形计算方法和代数曲线相同。

3.2 实例分析

以单位圆[l（t）=（sint，cost）Tt∈[0，2π]]及其上半圆弧为例展示伸缩因子作用的效果。图10为圆弧沿法矢方向的周期变形效果，将参数区间[[0，π]]十等分构造等分区间作为支持区间，根据式（3）计算变形结果。计算步骤如下：①将参数区间[[0，π]]十等分，记区间[[ti，ti+1]]为第i个变形区間;②计算区间[[ti，ti+1]]的中点[tim]，以[tim]为单峰值点构造伸缩因子函数;③ 计算区间[[ti，ti+1]]的圆弧点单位法矢和伸缩因子[E（t）];④根据公式（3）计算圆弧上各点变形后的位置。

图11为圆弧通过周期变形设计具有艺术形状的产品外形，实现一定的艺术效果。通过将单位圆周20等分，计算圆弧上点沿法矢方向的伸缩变形，峰值区间长度为每个周期支撑区间长度的1/3。其中曲线a为圆弧上点沿单位法矢方向的变形结果，曲线b为圆弧上点沿单位法矢反方向的变形结果。

图12展现了空间螺旋线[l（t）=（t，cost，sint）Tt∈[0，4π]]的变形效果。选取区域峰值伸缩因子实现螺旋线的局部拉伸变形。图13展示了通过调整伸缩参数h对Bézier曲线（a）进行伸缩变形的效果。其中，支撑区间为[0.3，1]，峰值点为0.75，设置伸缩参数h=3和5得到曲线b和c的变形效果。

3 结语

本文通过对曲线上的每个点进行逐点变换计算变形结果。通过定义伸缩函数和伸缩因子，推导曲线的自由变形控制方程，进而通过调节变形参数的方式产生丰富的变形效果。与已有工作相比，本文提出的方法不仅适用于参数曲线，同样适用于代数曲线，拓展了伸缩变形方法的适用范围。伸缩因子驱动曲线变形方法无需借助外部载体就能精确控制变形范围，简化了变形操作，变形效果丰富。在今后的研究中，将重点研究曲线在给定几何约束下的伸缩变形技术，建立约束条件下的曲线变形控制方程，实现曲线精准变形。

参考文献：

[1] BARR A H. Global & local deformations of solid primitives[J]. Computer Graphics， 1984， 18（3）： 21-30.

[2] SEDERBERG T W， PARRY S R. Free-form deformation of solid geometric models [J]. Computer Graphics， 1986， 20（4）： 151-160.

[3] PIEGK L. Modifying the shape of rational b-splines[J]. Part 1： curves. Computer Aided Design， 1989， 21（8）：509-518.

[4] AU C K，YUEN M M F. Unified approach to NURBS curve shape modification [J]. Computer Aided Design， 1995， 27（2）：85-93.

[5] SáNCHEZ-REYES J. A simple technique for NURBS shape modification [J]. Computer Graphics and Applications， 1997， 17（1）：52-59.

[6] 蒋大为. 有理 Bézier 曲线的权因子计算[J]. 航空学报， 1993，14（11）：666-669.

[7] 闫艳. NURBS曲线形状修改的研究[J]. 信息工程大学学报，2013， 14（6）：647-651.

[8] 张世杰， 张莉， 于立萍， 等. 渐进迭代逼近方法在曲线变形上的应用[J]. 中国图象图形学报， 2018， 23（11）： 1697-1706.

[9] GUAN Z D， JING L， NING T， et al. Study and application of physics-based deformable curves and surfaces [J]. Computers & Graphics， 1997， 21（3）：305-313.

[10] 经玲， 席平， 唐荣锡. 有限元方法在变形曲线曲面造型中的应用[J]. 计算机学报， 1998， 21（3）： 245-251.

[11] 王青， 柯映林， 李江雄. 基于力密度方法的NURBS曲线和曲面变形框架[J].？机械工程学报，2007， 43（3）： 135-142.

[12] 程仙国， 刘伟军. 外载荷的 B 样条曲线变形[J]. 中国图象图形学报， 2011， 16 （5）： 898-902.

[13] WANG X P， YE Z L， HU X M， et al. Shape modification and deformation of parametric surfaces[J]. Computer Aided Drafting， Design and Manufacture， 2002， 12（1）： 1-7.

[14] WANG X P， ZHOU R R， YE Z L， et al. Shape modification of parametric curves[J]. Chinese Journal of Aeronautics，2004，17（4）： 251-259.

[15] 宋来忠，彭刚，杨文颖， 等. 用于参数曲线自由变形的新的伸缩因子[J]. 工程图学学报， 2009， 30（3）： 87-93.

[16] 陆友太， 周来水，王志国，等. 基于乘幂伸缩因子的参数曲线自由变形[J]. 南京航空航天大学学报， 2011， 43（6）： 793-798.

[17] 陆友太，周来水，王志国，等. 基于多项式伸缩因子的参数曲面自由变形[J]. 中国机械工程，2012，23（5）： 609- 613.

[18] 张莉， 余慧芳， 檀结庆. 带平台伸缩函数的参数曲线变形[J]. 中国图象图形学报， 2015， 20（10）：1374-1383.

[19] 陈素根，刘兵兵. 参数曲面多边形区域上自由变形的多项式伸缩因子方法[J]. 安庆师范大学学报（自然科学版），2018，24（1）： 1-5.

[20] 李军成. 基于伸缩因子的代数曲线曲面变形方法[J]. 计算机工程与科学， 2016， 38（6）： 1225-1230.

（责任编辑：杜能钢）