软弱破碎围岩隧道开挖工法比选研究
2020-07-26罗燕平
罗燕平
(四川川交路桥有限责任公司,四川 德阳 618000)
0 前 言
软弱破碎围岩在隧道施工过程中一直是重难点问题,因其具有强度低、承载能力差、粘结力差、遇水易软化、岩体结构面比较软弱以及容易导致滑塌等工程地质特点成为大量专家学者关注的焦点[1-2]。艾光读[3]依托陈家店隧道工程,选择了四种软弱围岩隧道施工方法即台阶法、CD法、CRD法、双侧壁导坑法,并对这四种软弱围岩隧道施工方法展开了研究,结合实际工程地质条件,提出了最优的施工方法即双侧壁导坑法。叶权[4]依托云南省丽江文笔山隧道的喷锚暗挖台阶法施工段,采用有限元分析软件,对软弱围岩施工段隧道初期支护沉降进行技术研究,通过监控量测对实际施工工况下的断面进行数据收集,分析了锁脚锚杆的支护作用理论。高艳花[5]依托青峰软岩隧道,提出了相应的施工工法、掌子面稳定对策、拱脚稳定控制技术、合理刚度及强度支护措施等软岩隧道施工大变形系统控制技术,并采用数值模拟及现场监测手段,研究了上述系统控制技术对软弱围岩隧道大变形的控制效果。本文依托金家庄特长螺旋隧道工程,通过数值模拟比选两台阶法和三台阶预留核心土法两种施工方法,讨论适合该隧道的最优开挖工法。
1 工程概况
金家庄特长隧道位于河北省张家口市赤城县炮梁乡砖楼村东、金家庄村西北方向,全长4 104 m,隧道最大埋深约314.5 m,隧道区地表标高为1 406~1 738 m,相对高差332 m,入口端洞口坡度为16°~24°,出口端洞口坡度为26°~31°。隧道区地层主要为海西期二长花岗岩,局部为第四系覆盖层。
本文以K82+100~K82+180为研究标段,该标段内隧道横断面采用两台阶法和三台阶预留核心土法进行模拟开挖,进行开挖工法的比选。
2 隧道开挖数值模拟
2.1 计算模型建立
本次计算以金家庄特长螺旋隧道K82+100~K82+180段作为设计依据建立模型。隧道开挖宽度为13.83 m,高度为12.09 m。根据圣维南原理,隧道开挖计算模型的边界通常取开挖洞径的5~7倍[7]。本次建模中左右边界取至距隧道边墙80 m,上边界取至距隧道拱顶80 m,下边界取至距隧道拱底以下80 m,模型沿隧道轴向拉伸50 m。模型单元全部采用具有个8节点的6面体三维实体单元,计算模型总共包含153 100个单元和157 233个节点,计算精确度可以得到保证。各个施工工法计算模型见图1。为了真实地模拟隧道所处的地应力场,模型下边界采用约束竖向位移的位移边界条件,顶面采用与上覆围岩重度等效的应力边界条件、侧面根据不同侧压力换算成相应的边界条件。
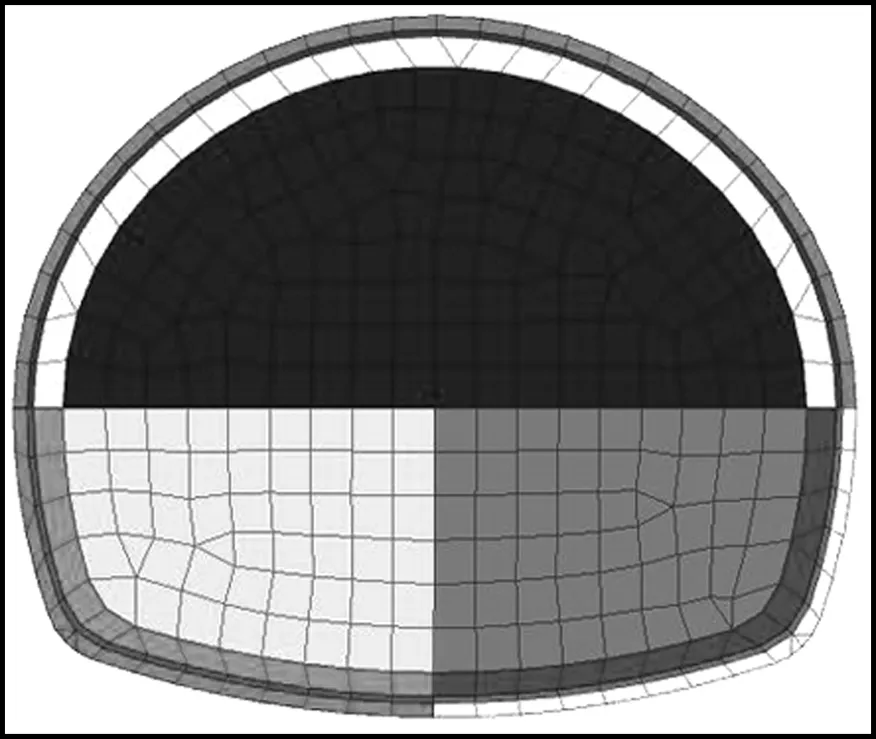
(a)两台阶法网格划分
2.2 开挖工法步序
本文针对金家庄特长螺旋隧道,采用两台阶开挖法、三台阶预留核心土开挖法进行数值模拟(见表1)。

表1 隧道开挖计算工法一览表 单位:m
2.3 模型计算参数选取
计算中将隧道围岩视为均质、单一材料各向同性的连续介质,采用摩尔-库伦(Mohr-Coulomb)弹塑性本构模型来描述。通过FLAC3D中的空模型来实现围岩的开挖。
根据《公路隧道设计规范》(JTG D70—2014)和金家庄特长螺旋隧道地质勘察资料并做相应调整,本次计算选取的围岩和隧道结构的物理力学参数如表2所示,锚杆物理力学参数如表3所示。
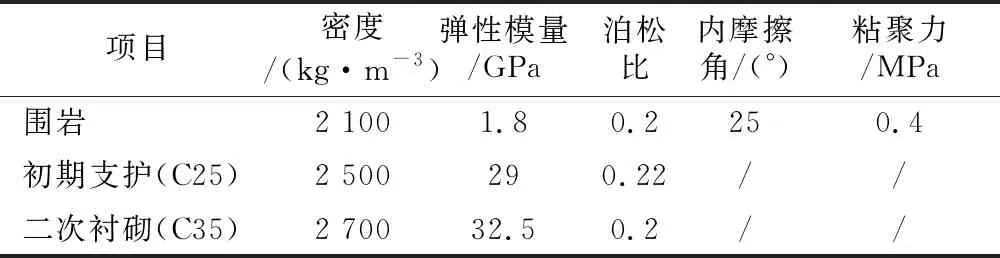
表2 围岩、初期支护和二次衬砌物理力学参数

表3 锚杆物理力学参数
3 数值计算结果
本次计算选取监测断面位于模型Y=40 m处,并在洞周布置8个监测点,记录开挖过程中围岩及支护结构的应力及位移变化,断面监测点位置布置图如图2所示。
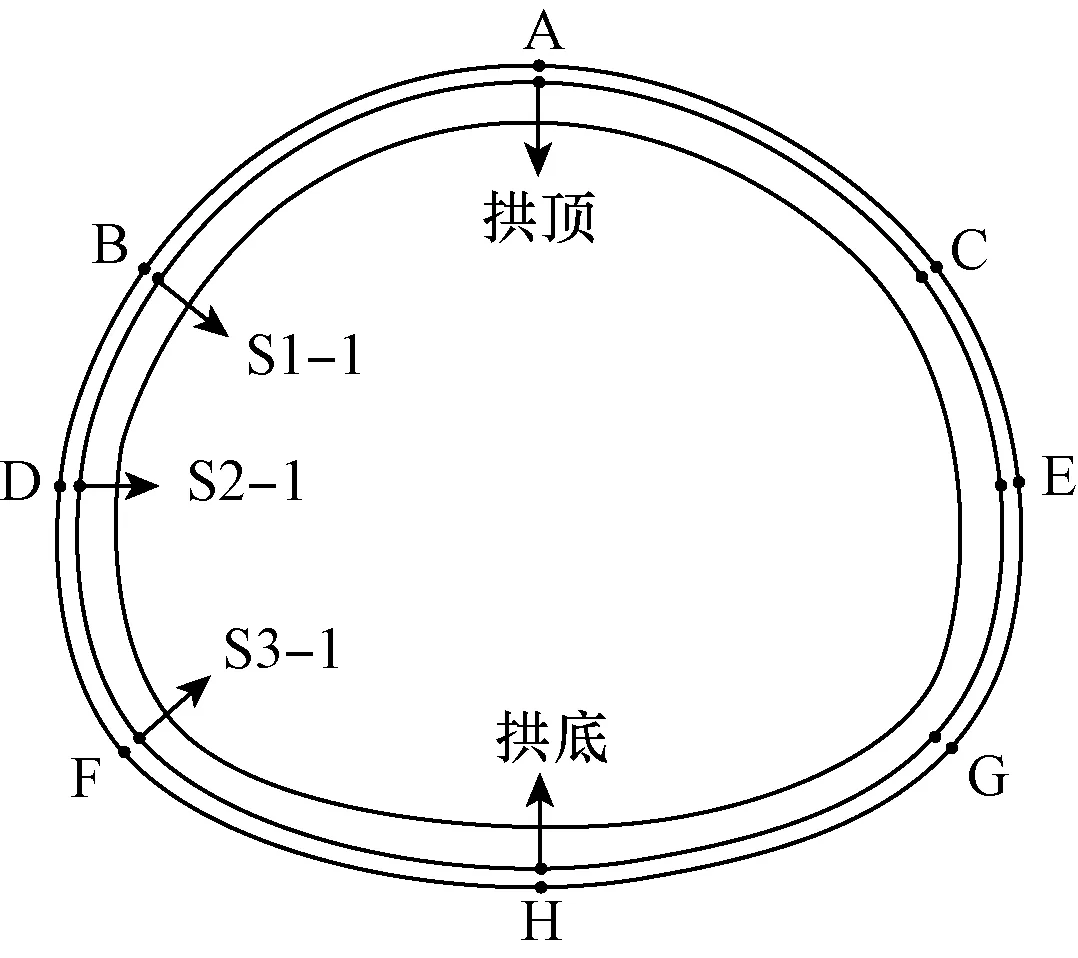
图2 监测点位置示意图
3.1 隧道洞周位移
位移监测数据见表4。从表4可以看出,两种工况下的洞周围岩位移大致相同。对于相同监测点位,工况2(两台阶法)的位移明显高于工况1(三台阶预留核心土法)的位移,这是因为采用三台阶预留核心土法一次开挖面积较小,有利于掌子面稳定,同时能够更加及时的给围岩提供支护阻力,控制围的变形。
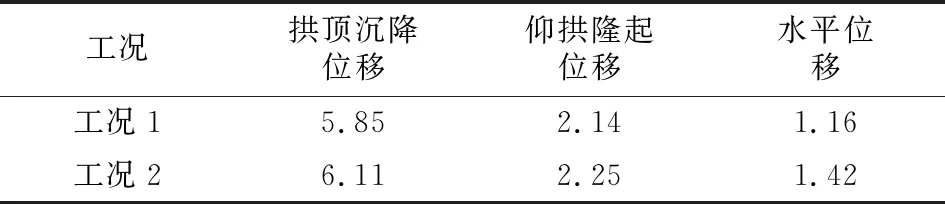
表4 洞周位移监测数据 单位:cm
3.2 隧道洞周应力
采用三台阶预留核心土法隧道开挖围岩洞周应力分布云图见图 3所示。

(a)最大主应力
采用两台阶法隧道开挖围岩洞周应力分布云图见图4。
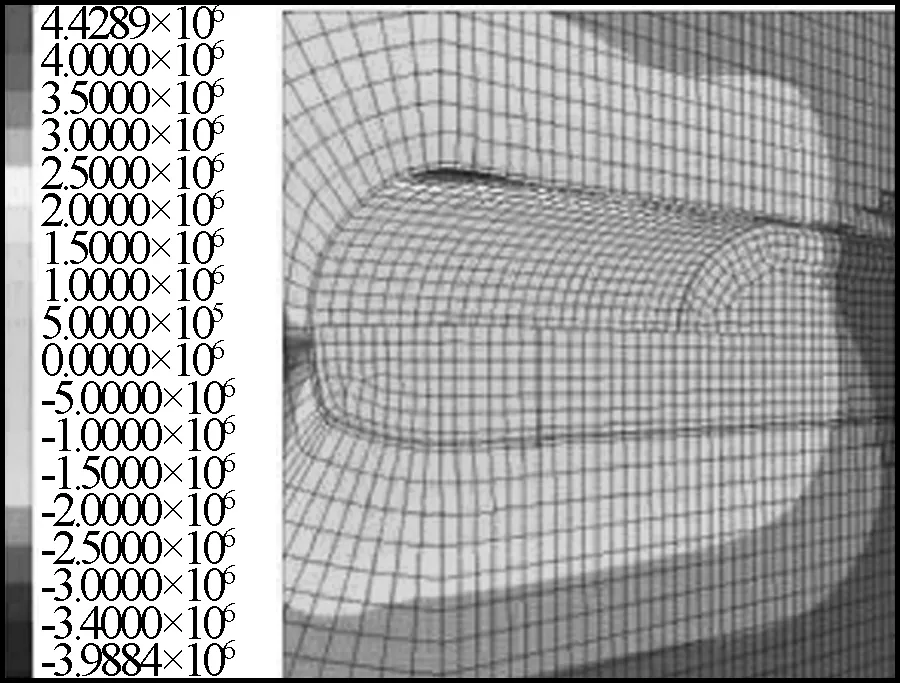
a)最大主应力
由图3~4可知,开挖完成后三台阶预留核心土法围岩最大主应力5.72 MPa,位于拱顶和仰拱,最小主应力-5.46 MPa,位于洞周距拱顶和拱底一定距离的位置。两台阶法最大主应力4.51 MPa,位于拱顶和仰拱,最小主应力-5.04 MPa,位于洞周距拱顶和拱底一定距离的位置。对比两种工法的洞周围岩应力可知,两台阶法最大、最小主应力均小于三台阶预留核心土法。两台阶法施工对围岩的扰动明显小于三台阶预留核心土法,围岩所需承受的主应力要优于三台阶预留核心土法。
3.3 初期支护内力对比
各工况下初期支护最大最小主应力值及其分布位置见表5。

表5 初期支护最大最小应力及分布位置 单位:MPa
由表5可以看出,两种工况下得到的初期支护应力大小和分布有所不同。工况1(三台阶预留核心土法)较工况2(两台阶法)的最大、最小主应力分别增加了18%和34%,说明两台阶法控制隧道初期支护的变形优于三台阶预留核心土法。
3.4 初期支护位移(见图5~6)对比

图5 工况1初支位移曲线

图6 工况2初支位移曲线
从图5~6可以看出,工况1(三台阶预留核心土法)下隧道初期支护各监测点最大位移为20 mm,位于左拱脚;初期支护整体位移分布情况:拱脚位移>边墙位移>拱肩位移>拱顶和仰拱位移。位移最小值位于拱顶;工况2(两台阶法)下隧道初期支护最大位移只有14 mm左右,位于拱脚;初期支护洞周位移分布均匀,拱顶沉降受较大的围岩水平侧向压力和二次衬砌施加的影响,其值有所减小,初期支护整体位移分布情况:拱脚位移,边墙位移,仰拱位移>拱肩位移>拱顶位移。
对比两种工况下初支位移曲线,工况1(三台阶预留核心土法)开挖初期支护位移相比工况2(两台阶法)开挖增加了30%,说明两台阶法相比三台阶预留核心土法施工扰动小,能控制了隧道初期支护的边墙及拱脚的变形情况。
3.5 二次衬砌内力对比
各工况下二次衬砌支护最大最小主应力值及其分布位置见表6。

表6 二次衬砌最大最小应力及分布位置 单位:MPa
由表 6可以看出,两种工况下得到的二次衬砌应力大小和分布差异不大,二次衬砌应力的分布情况比较相似,且二次衬砌在整个支护体系中受力相对较小,说明其主要作用仍是作为安全储备。同时,计算时弹性单元模拟二次衬砌,实际中不管是混凝土还是钢架都不是理想的弹性体,故而模拟出来的二次衬砌应力会比实际偏大。
3.7 围岩塑性区对比
隧道在开挖的过程中,必然会引起围岩应力的重分布,其中部分围岩因发生应力集中现象,导致围岩应力超过其屈服强度,从而产生不可恢复的屈服区域,形成围岩塑性区。图 7为上台阶开挖至Y=40 m(Y表示距离洞口的距离)、开挖完成后的工况1、工况2条件下围岩塑性区分布,表7为围岩塑性区体积。

(a)工况1塑性区

表7 两种工况施工完成后围岩塑性区体积 单位:m3
对比两种工况的结果可以发现,工况1(三台阶预留核心土法)最终塑性区范围比工况2(二台阶法)最终塑性区范围大了14%,说明两台阶法在开挖过程中对围岩的扰动更小;从塑性区的分布看,三台阶预留核心土法塑性区分布范围更少,更利于控制围岩的稳定。
3 结 论
本文结合金家庄特长螺旋隧道工程现场工法(三台阶预留核心土法和两台阶法),借助FLAC3D有限元差分软件分别对金家庄螺旋隧道现场施工工法进行开挖数值模拟,对比分析了两种工法下隧道围岩的位移、应力、初支、二衬内力、围岩塑性区分布等,得到各工法下隧道施工的力学特性,并对施工工法进行工法比选,得到以下结果。
1)在控制围岩变形方面,由于三台阶预留核心土法开挖能够迅速施作支护结构[6],及时提供支护作用,改善了支护结构受力,使支护结构能够及早承担围岩应力,控制隧道变形速率,从而减小了隧道整体变形,故在控制围岩变形方面,三台阶预留核心土法优于两台阶法。
2)从隧道开挖后围岩应力分布状态可以看出,三台阶预留核心土法开挖后围岩的大小主应力明显高于两台阶法,这是由于三台阶预留核心土法开挖面较多,对围岩扰动较大所造成的[7]。
3)对比两种工法的塑性区结果可以发现,三台阶预留核心土法最终塑性区范围比两台阶法最终塑性区范围大了14%。说明两台阶法在开挖过程中对围岩的扰动更小;从塑性区的分布看,三台阶预留核心土法塑性区分布范围更少,更利于控制围岩的稳定。
4)对比两种工法下初期支护内力可知,三台阶预留核心土法初期支护内力明显大于两台阶法,这是因为三台阶预留核心土法开挖后支护比较及时,在短时间内承担围岩所释放的应力,控制住了围岩的变形,保证了施工时的安全;而两台阶法由于支护没有三台阶预留核心土法及时,故当其进行初期支护时,围岩已经释放了一部分应力,所以就初期支护应力而言,两台阶法要小于三台阶预留核心土法,但对于安全性而言,三台阶预留核心土法优于两台阶法。
由此可见,对比两种工法,两台阶法更适宜于围岩较稳定,掌子面揭露情况较好的情况;三台阶预留核心土法更适宜于围岩较差,需及时对围岩进行支护的情况。对于金家庄特长螺旋隧道,建议根据围岩等级合理确定具体施工方法。针对金家庄特长螺旋隧道,当围岩级别为S4a1,S4a2时,建议采用两台阶法施工;当围岩级别为S5a,S5b时,建议采用三台阶预留核心土法。
[ID:009879]
