插值切割位场分离方法改进及其在资料处理中的应用

2020-07-26赵文举赵荔杨战军陶德强

物探与化探 2020年4期

赵文举，赵荔，杨战军，陶德强

(中国石油东方地球物理勘探有限责任公司综合物化探处，河北涿州 072751)

0 引言

随着计算机的广泛应用，重磁异常分离方法早已经由手动发展为自动，且方法众多。广义来说，改变量纲的位场变换方法也属于位场分离，这里我们讨论的主要是不改变量纲的分离方法。主要有波数域[1]和空间域两种，波数域方法如温纳滤波[2]、匹配滤波[3-4]、小波逼近[5-6]、正则化滤波[7]、巴特沃斯滤波等，空间域方法如最小二乘法[8]、窗口滑动平均法、趋势分析法、圆周平均法、插值切割法等众多方法，不胜枚举。

插值切割法[9]由文百红等人提出，该方法采用圆周上的4个正交点值以及半径来构建切割算子，由于其引入的半二阶差分量与负二阶水平导数成正比，因此，其对位场的不同非线性部分有不同的作用，从而提高了对不同特征重磁异常的分辨率。该方法近年来在位场数据的去噪、半定量分离等方面被应用，甚至用于估计场源体的深度和三维成像[10-17]。

笔者首先介绍插值切割的原理。其次，就该方法在模型和实际应用时所碰到的问题进行了部分改进，并对改进前后的效果进行了对比分析。最后，给出了该方法在深层构造异常提取和火成岩三维成像方面的应用实例，取得了较好的应用效果。

1 方法原理

1.1 基本原理

图1中g0是某点的重力异常值，g1，g2，g3和g4是半径为r的周围4个点的异常值，用下列公式计算g0点第一次切割的区域场：

图1 插值切割法示意Fig.1 Interpolating cut method

(1)

(2)

α=f(g0,g1,g2,g3,g4),

(3)

其中：α是与g0，g1，g2，g3，g4有关的函数。

α=b+c，

δgx=g1-g3, δgy=g2-g4。

由此得出全区的第一次切割的区域场R1。用R1取代原来的异常场，再用式(1)～(3)计算得到第二次切割的区域场R2。如此迭代，最后有

实际切割次数约50～100次。最后得到局部场L，L=g-R。

由于切割算子中的α系数引入了半二阶差分量，它们与负二阶水平导数即曲率成正比，因此插值切割对不同非线性异常部分有不同的作用，从而提高了对不同特征异常场分离的分辨率。

1.2 分离效果对比

为了说明插值切割方法的分离效果，对理论模型数据和实际数据进行了异常分离，并与上延法和趋势分析等常用异常分离方法进行了对比。图2a为理论局部磁异常，图2b图为理论区域磁异常，二者相加得到理论的局部磁异常与区域磁异常的叠加异常(图2c)。

a—理论局部磁异常；b—理论区域磁异常；c—理论叠加磁异常a—theoretical local magnetic anomaly；b—theoretical regional magnetic anomaly；c—theoretical superposition magnetic anomaly

为了从叠加异常中分离出局部异常与区域异常，利用插值切割方法进行了不同切割半径下的分离实验。当切割半径为150 m、切割次数100次时，分离出来的局部磁异常与理论局部磁异常无论在异常幅值以及形态上都具有极大的一致性，分离效果极佳。区域异常的分离效果也很好，形态和幅值上均相当，只是分离处理的区域磁异常的梯度较理论模型小一些。图3展示了利用插值切割(图3b)、向上延拓(图3c)、趋势分析(图3d)等方法分离的局部和区域磁异常与理论异常(图3a)的对比情况，其中向上延拓分离时的区域场为上延250 m确定，趋势分析分离的区域场为1阶多项式确定。实验表明，插值切割方法有对所设计模型的局部和区域场进行分离的能力，较一般方法有优越性。

图3展示了插值切割方法对理论模型异常的分离能力，下面再简单对比一下实际资料的处理效果。东北某区磁异常比较发育，火成岩的磁异常叠加于区域场上，分别利用插值切割、向上延拓和趋势分析3种方法进行火成岩引起的局部磁异常的分离。图4展示了该区化极磁异常(图4a)以及插值切割(图4b)、向上延拓(图4c)、趋势分析(图4d)方法分离的区域场和局部场。其中插值切割选取的切割半径为1 km、切割次数为100次，向上延拓分离的区域场为上延1 km，趋势分析分离的区域场的多项式阶次为2阶。对比局部场的分离效果，插值切割分离的局部磁异常在异常细节表现力和分辨率等方面都优于其他两种常用方法。

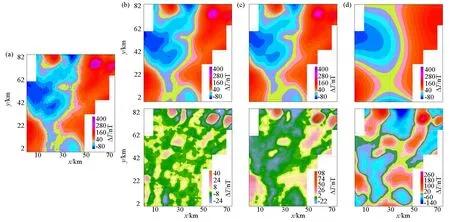
a—某区化极磁异常；b—差值切割分离的区域场(上)及局部场(下)；c—向上延拓分离的区域场(上)及局部场(下)；d—趋势分析分离的区域场(上)及局部场(下)a—abnormal magnetic polarization of a certain region；b—regional field (upper) and local field (lower) separated by interpolation cutting；c—regional field (upper) and local field (lower) separated by upward extension；d—trend analysis separate regional field (upper) and local field (lower)

a—理论区域场(上)及局部区域场(下)；b—差值切割分离的区域场(上)及局部场(下)；c—向上延拓分离的区域场(上)及局部场(下)；d—趋势分析分离的区域场(上)及局部场(下)a—theoretical regional field (upper) and local field (lower);b—the regional field (upper) and local field (lower) separated by interpotation cutting；c—continue upward to separate the regional field (upper) and local (lower)；d—regional field (upper) and partial (lower) separated by trend analysis

2 改进方案及效果

插值切割方法虽然在异常分离上较一般方法具有一定的优势，但仍存在一些问题。笔者采用模型的计算来说明并给出改进前后的对比。图5为深浅不同磁性磁源的叠合模型，3个绿色方块(磁性0.05SI)为浅部磁源，产生局部磁异常，一个紫色椭圆(磁性0.1 SI)为深部磁源，产生区域磁异常。叠加异常如图6所示。

图5 深浅源不同磁性叠合模型Fig.5 Different magnetic superposition models of deep and shallow sources

图6 叠合模型产生的磁异常Fig.6 Magnetic anomaly generated by superposition model

2.1 区域场圆滑

模型和实际数据应用中发现，切割算子获得的区域场往往会带有高频的抖动，这与区域场的光滑性相矛盾。针对这一现象，在获得区域场后，采用切割窗口大小的滑动平均法进行光滑获得区域场，进而获得局部场。由图7可看出圆滑前后对比情况，区域场的光滑性得到改善，进而分离的局部场也不会引入额外的高频噪声，区域场圆滑后获得的局部场明显得到改善。

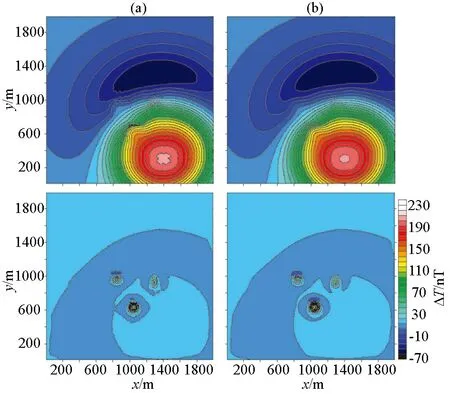
a—圆滑前区域场(上)及局部场(下)；b—圆滑后区域场(上)及局部场(下)a—smooth front regional field (upper) and local field (lower)；b—smooth posterior regional field (upper) and local field (lower)

2.2 八方位切割

插值切割的算法是四方位(EW—SN)切割，实际应用中发现四方位切割会引起区域场的整体形态畸变，针对这个问题，采用八方位切割来解决(图8)，即在原四方位(EW-SN)切割的基础上，增加NE—NW正交方向的切割运算，半径上的异常值(g1′、g2′、g3′、g4′)采用双线性插值方法确定，区域场值g0′采用与四方位切割相同的公式计算，这里不进行赘述。最终的区域场值采用两组方向(EW—SN和NE—NW)切割算子的平均值(g0′/2+g0/2)代替。

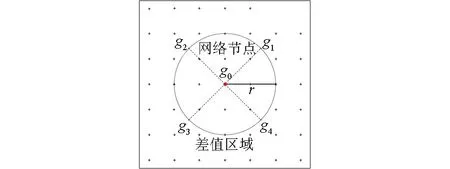
图8 八方位切割原理示意Fig.8 Eight-position interpolation cutting method

图9展示了八方位切割前后对比情况。a上图为四方位切割的区域场，区域场形态趋近方形，b上图为八方位切割的区域场，区域场的形态更接近于椭圆形，与源的形状相同。a下图和b下图分别为四方位、八方位切割的局部场。

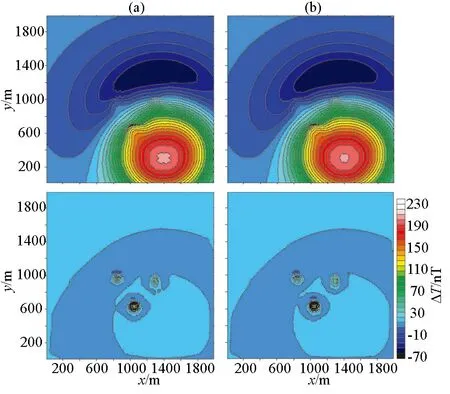
a—四方位切割的区域场(上)及局部场(下)；b—八方位切割的区域场(上)及局部场(下)a—regional field (upper) and local field (lower) cut by the square；b—regional field (upper) and local field (lower) cut by octagonal position

2.3 任意实数半径

原插值切割算法的半径一般按点距的整数倍(如1dx、2dx、…)进行选择，这种设置方法在去噪处理中不适用，过大的切割半径不仅会消除噪声，也会对有效信号进行过度滤除。针对这个问题，采用实数倍点距(如0.1dx、1.3dx、…)作为半径，相应半径上的异常值采用双线性插值方法确定。图10a为加入噪声(均值0，标准差1 nT)的叠加磁异常图。从图10b、c中局部异常形态和幅值的对比可以明显看出，利用0.5倍点距半径滤波后的磁异常不仅去除了噪声，而且对有效信号的幅值最小程度地削弱。

a—加入噪声的叠加磁异常；b—1倍点距半径滤波后的磁异常；c—0.5倍点距半径滤波后的磁异常a—superposition magnetic anomaly with added noise；b—magnetic anomaly after 1 radius of point distance filtering；c—magnetic anomaly after 0.5 times of point distance radius filtering

3 实际应用效果

3.1 重力异常半定量分离

中国西部某区域地表复杂，地震地质条件极差，地震资料的品质较差，难以解决问题。为了加快该区油气勘探的步伐，于2007年部署高精度重磁勘探，测网500 m×200 m，重力异常精度0.027 mGal，磁异常精度1.26 nT。2011年经过钻井和地震联合攻关，确定了1 500 m左右深度的浅部构造，构造形态见图11中的黑色虚线。

从图11a可见，地震构造没有与布格重力异常的任何高异常点吻合，并且偏差很大。为了研究插值切割方法对不同深度异常的提取能力，利用不同半径提取的局部重力异常获得了代表不同深度段的重力异常图，并通过向下延拓方法将不同深度异常延拓至对应深度顶面。图11中b、c、d、e、f、g分别代表200～600 m、600～1 000 m、1 000～1 400 m、1 400～1 800 m、1 800～2 200 m、2 200～2 600 m深度段的重力异常。从这些异常与地震构造的对比来看，图11e是1 400～1 800 m深度的重力异常与地震构造吻合最好，而且深度也基本吻合。这反映了插值切割算法的异常半定量分离能力。

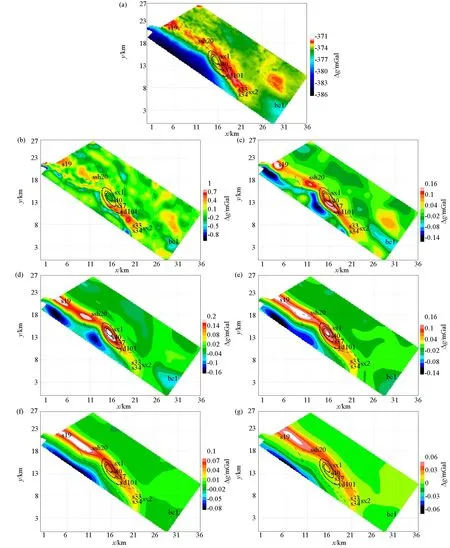
a—布格重力异常；b—200～600 m深度重力异常；c—600～1 000 m深度重力异常；d—1 000～1 400 m深度重力异常；e—1 400～1 800 m深度重力异常；f—1 800～2 200 m深度重力异常；g—2 200～2 600 m深度重力异常a—bouguer gravity anomaly; b—gravity anomaly at depths of 200～600 m; c—gravity anomaly at depths of 600～1 000 m; d—gravity anomaly at depths of 1 000～1 400 m; e—gravity anomaly at depths of 1 400～1 800 m; f—gravity anomaly at depths of 1 800～2 200 m; g—gravity anomaly at depths of 2 200～2 600 m

3.2 磁异常三维成像

南祁连盆地位于祁连山南部，南部隔宗务隆山与柴达木盆地相邻，西北部紧邻阿尔金山，北东通过中祁连地块与河西走廊相望(图12)。该盆地是在加里东褶皱基底上发育起来的山间盆地，石炭系—三叠系为地台期一套相对稳定的浅海相和海陆交互相沉积，侏罗系—白垩系缺失，上新近系—第四系为陆相沉积。研究区的磁性体主要发育在志留系，岩性为千枚状凝灰岩、千枚岩和安山岩等，磁化率达到 (1 000～1 600)×10-5SI。磁异常主要是志留系基底内部磁性体的反映。ΔT磁异常经过化极处理后得到了化极磁异常图，见图13，它主要反映了志留系磁性体的分布。

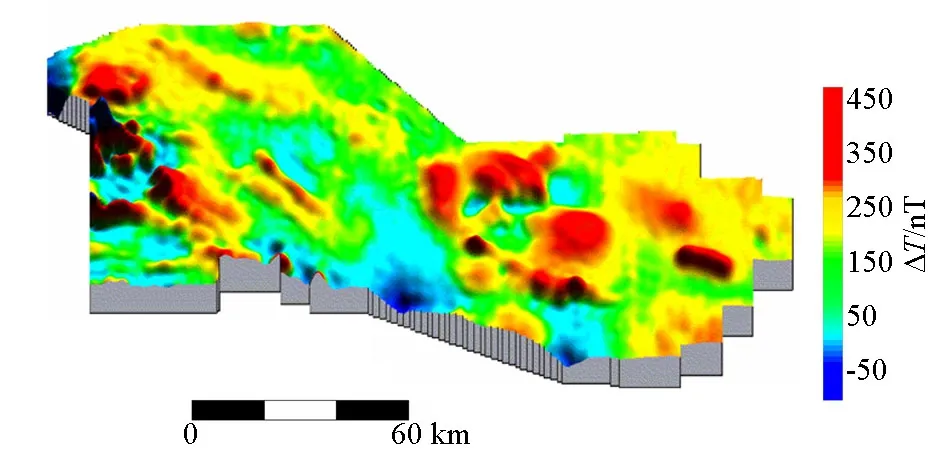
图13 化极磁异常Fig.13 RTP magnetic anomaly

图12 研究区构造位置Fig.12 Schematic location of study area

常规的重磁资料处理，可以获得较为可靠的构造平面展布信息，深度计算一般采用剖面正反演或基于规则模型的特征点法，它们的精度或依赖于已知控制点成果，或依赖于异常与典型模型的符合程度，而且由于计算和反演周期较长，往往仅作数条剖面。为了解决上述问题，我们引入了插值切割法，通过插值切割三维成像研究区内火成岩的三维空间分布。

根据前人关于插值切割数据与地质体深度密切相关的研究成果，我们把不同切割半径的插值切割数据赋予相应的深度概念，构建三维数据体，在一定程度上反映了地质体的三维空间特征，即地质体三维磁成像。三维成像数据体构建采用以下步骤：

1) 以异常数据网格距及其整倍数作为切割半径,采用插值切割法分别对异常场求取局部场和区域场；

2) 以对应各切割半径的局部场(也可用减去上一切割半径的局部场的插值)作为异常，以切割半径作为深度，建立各深度的异常数据体；

3) 将各深度的异常数据体组成三维数据体；

4) 采用三维显示软件对异常进行显示，就获得异常三维成像。

图14是插值切割三维磁成像，图中红色表示磁异常强度大，一定程度上代表了磁化率高，异常空间展布表示了磁性体的三维空间分布。可以看出，三维成像很好地反映了该区火成岩的空间分布特征。