改进的小波阈值法及其在地震数据降噪处理中的应用
2020-07-26刘剑秦飞龙
刘剑,秦飞龙
(1.成都工业学院 汽车与交通学院,四川 成都 611730; 2. 成都工业学院 大数据与人工智能学院,四川 成都 611730; 3.电子科技大学 数学科学学院,四川 成都 611731)
0 引言
社会的发展离不开能源,能源的获取大多是通过地质勘查所得。但是,在野外勘查中,采集到的地震数据会受到各种不可预知的因素干扰,如地质环境,机器设备,人为影响等,使得地震数据混合着强烈的随机噪声,地震数据记录剖面分辨率低,地震数据信噪比低,不利于对地震数据后期解释,从而必须要对野外地震数据进行降噪处理[1]。为了去除地震数据的随机噪声,一些学者利用随机噪声和有效信号的差异,构建了随机噪声去除模型,如傅里叶变换[2]、K-L变换[3]、倾斜叠加法[4]等,但是该类方法在地震数据降噪中存在着一定的缺陷,因为这些方法要求明确数据的先验知识,实际上地震数据伴随各种干扰,如机器影响,人为影响,地质环境影响等,使得地震信号情况是无法预知的。因此,该类型算法对地震数据降噪效果不理想[5]。盲信号分离技术是近二十年来发展的一种有效降噪方法,如ICA降噪方法[6],FASTICA降噪算法[7],JADE降噪算法[8]等,它的最大优势是不需要知道信号是如何混合的前提下,就能分离出目标信号。但是该类算法具有一个缺陷,它需要处理的混合信号是相互独立的,混合程度不能过于复杂,还要求信号中最多只有一个是非高斯信号[1,9]。但地震信号由于所处地质环境十分复杂,各种干扰影响严重,混合信号彼此之间并非相互独立,混合程度也极强。从而,盲源分离方法对地震数据降噪不理想。近年来,小波变换越来越广泛应用于地震数据降噪,因为小波变化具有自适应“时间—频率”窗口优势[10],还能够将信号分解到不同频带上,如高频上的噪声信号和低频上的细节信号,这种分解方式可重复进行,信号在不同频带上通过选取小波阈值降噪法有利于将噪声进行消除,并且利用小波的重构变换能够将去除噪声后的有效信号恢复为原始信息[11-12]。其中,阈值降噪应用最广泛的是Donoho提出的软、硬阈值降噪法[13],但是软阈值函数是通过恒定方式压制噪声,容易去掉有效信号。而硬阈值函数在阈值出现不连续时,会给重构信号带来振荡,从而软、硬阈值函数进行信号降噪存在缺陷[14]。因此,文中在软、硬阈值函数基础上提出了一种改进的小波阈值降噪算法,以提高信号降噪效果。
1 改进的阈值算法
1.1 软、硬阈值算法基础
给定一组观测信号:
f(t)=s(t)+n(t) ,
(1)
式中:s(t)表示有效信号;n(t)为随机噪声信号;f(t)是观测信号,混合有噪声信号。
假设样本的采样点个数为N,那么f(t)的一维离散小波分解变换[14]如下所示:
(2)
式中,ψ(t)指一个母小波,Wf(j,k)指小波系数,记为Wj,k。对于一维的离散小波重构变换和二维小波变换详见文献[1]。对于观察地震数据,经过小波分解后的信号可以通过软、硬阈值法进行降噪处理,然后通过小波重构恢复原始有效信号[1]。
软、硬阈值函数方法如下[13,16]:
(4)
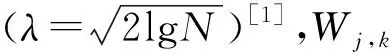
信号通过式(3)的软阈值处理后的小波系数具有连续性,但利用大于阈值的恒定方式进行噪声压制,会造成一些有效信号当作噪声信号被去除,以至于得出的信号不能代表真实信息。硬阈值函数可以避免软阈函数以恒定的压缩方式产生的偏差影响,但硬阈值函数在降噪上仍然具有缺陷,由式(4)可知硬阈值法降噪后的信号在阈值λ处是不连续的,会导致小波重构恢复原始信号时发生一定的振荡,使得原始有效信息光滑度变差。为了克服软、硬阈值函数在信号降噪的缺陷,成枢等提出了一种融合加权平均的改进小波阈值函数进行数据降噪,该方法在软阈值函数的基础上加入了1个可变的调节因子,达到更好的滤波效果[17],然而该方法在确定分解层数时依据经验公式可能会对信号降噪产生影响,并且该方法过于复杂,运算量较大。从而本文在软、硬阈值函数基础上,进一步对文献[17]的算法进行优化,得出了一种新的改进小波阈值降噪方法。
1.2 改进的阈值降噪方法
本文设计出的改进的小波阈值降噪方法如下:
(5)
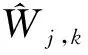
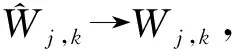
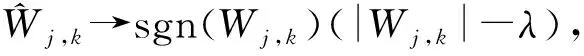
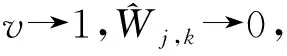

通过上述分析可知,文中提出的改进的小波阈值函数不仅具备了软、硬阈值函数的所有降噪功能,还避免了软、硬阈值函数降噪的缺点,因为它克服了以恒定方式产生的偏差的影响,而且在阈值处的函数具有连续性。该算法与文献[17]中的算法相比,算法更简洁,项数较少,利于运算,本文的算法是基于小波分解后的信号进行阈值降噪处理,后续还结合真实地震数据进行仿真实验得出小波分解层数。从而,本文提出的改进阈值函数数据降噪上更具有实际意义。
2 仿真实验
此处,通过仿真实验说明改进的小波阈值函数在信号降噪上的有效性,选取2 000个采样点,采样间隔为1 ms的样本数据,其有效信号m如图1a所示,在有效信号m上添加随机混合噪声信号得出混合观察信号,如图1b所示。通过图1b发现有效信号被随机噪声所覆盖,几乎分辨不出有效信号,利用本文提出的改进阈值算法以及软、硬阈值函数对观察信号x进行降噪处理,降噪后的信号如图2所示。由图2知,软、硬阈值函数能够去除部分噪声信号,但仍然有存在随机干扰噪声混合在有效信号上,降噪效果不理想,而改进的阈值函数能够去除所有干扰,有效信号的峰值毛刺干扰被消除,从而改进的小波阈值函数降噪效果较软、硬阈值函数降噪效果更佳。
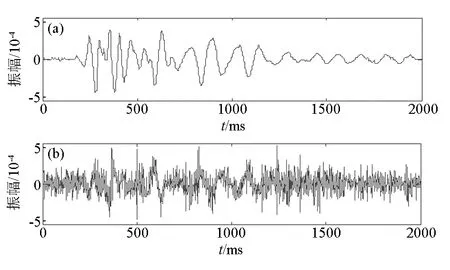
a—有效信号;b—带有随机噪声的观测信号a—effective signal;b—observation signal with random noise
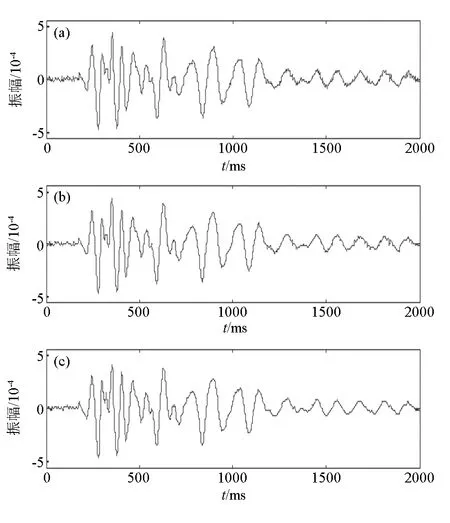
a—软阈值降噪;b—硬阈值降噪;c—改进的阈值函数降噪a—denoising with soft threshold function;b—denoising with hard threshold function;c—denoising with improved threshold function
信号降噪效果可通过信噪比(SNR)[18]和均方根误差(RMSE)[18]来评价,信噪比SNR方法:
(6)
均方根误差RMSE方法:
(7)
在式(6)和(7)中,x(k)表示原始观测数据,x′(k)指的是降噪后的数据,SNR越大,函数降噪效果越好,反之,SNR越小,降噪效果越差;RMSE越大,函数降噪效果越差,反之,RMSE越小,降噪效果越好。
通过式(6)和(7)得出改进的阈值函数,软、硬阈值法降噪后的SNR和RMSE结果(表1)。由表1可知,在所有SNR和RMSE中,改进阈值法的RMSE最小,SNR最大。从而,改进阈值法降噪效果最佳。在小波变换中还需要确定小波基,dbN系列和symN系列是最常用的小波基,尤其symN系列是地震数据降噪的常用小波基。因此,通过式(6)和(7),结合不同的symN小波基,得出改进阈值函数降噪后信号的SNR和RMSE(图3),由图3可知,在所有symN小波基中,改进阈值函数在sym3下的降噪后信号的SNR最大,RMSE最小,从而sym3作为改进阈值函数小波基,降噪效果最理想。
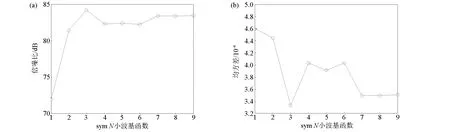
图3 不同symN小波基的信噪比(a)和均方根误差(b)Fig.3 The SNR(b) and RMSE(b) wih different symN
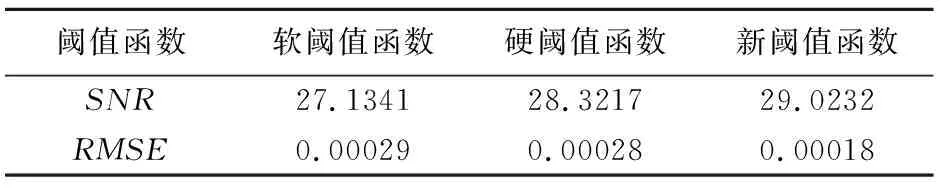
表1 不同阈值函数的信噪比和均方根误差
为了确定在新算法条件下的小波分解层数,选取第四部分实际地震数据中的第80道观测信号进行降噪处理,采样点为6 000,采样间隔为1 ms,为了便于显示,选取前3 000采样点进行说明(图4a),由图4a知,200~2 000 ms内存在地震波激发,但在0~200 ms和2 000~3 000 ms区间出现严重的毛刺现象,说明噪声干扰严重。从而选取sym 3为小波基,利用新算法分别进行1~5层小波分解降噪(图4b~ 4f)。由图4b~ 4f可知,分解层越高,新算法降噪能力越强,然而当分解4层以后,有效信号与观测信号波形不吻合,将噪声作为信号丢失,从而,对地震数据降噪,分解层数为3层时效果最佳,避免了文献[17]提出的算法由于分解层数不确定性影响。
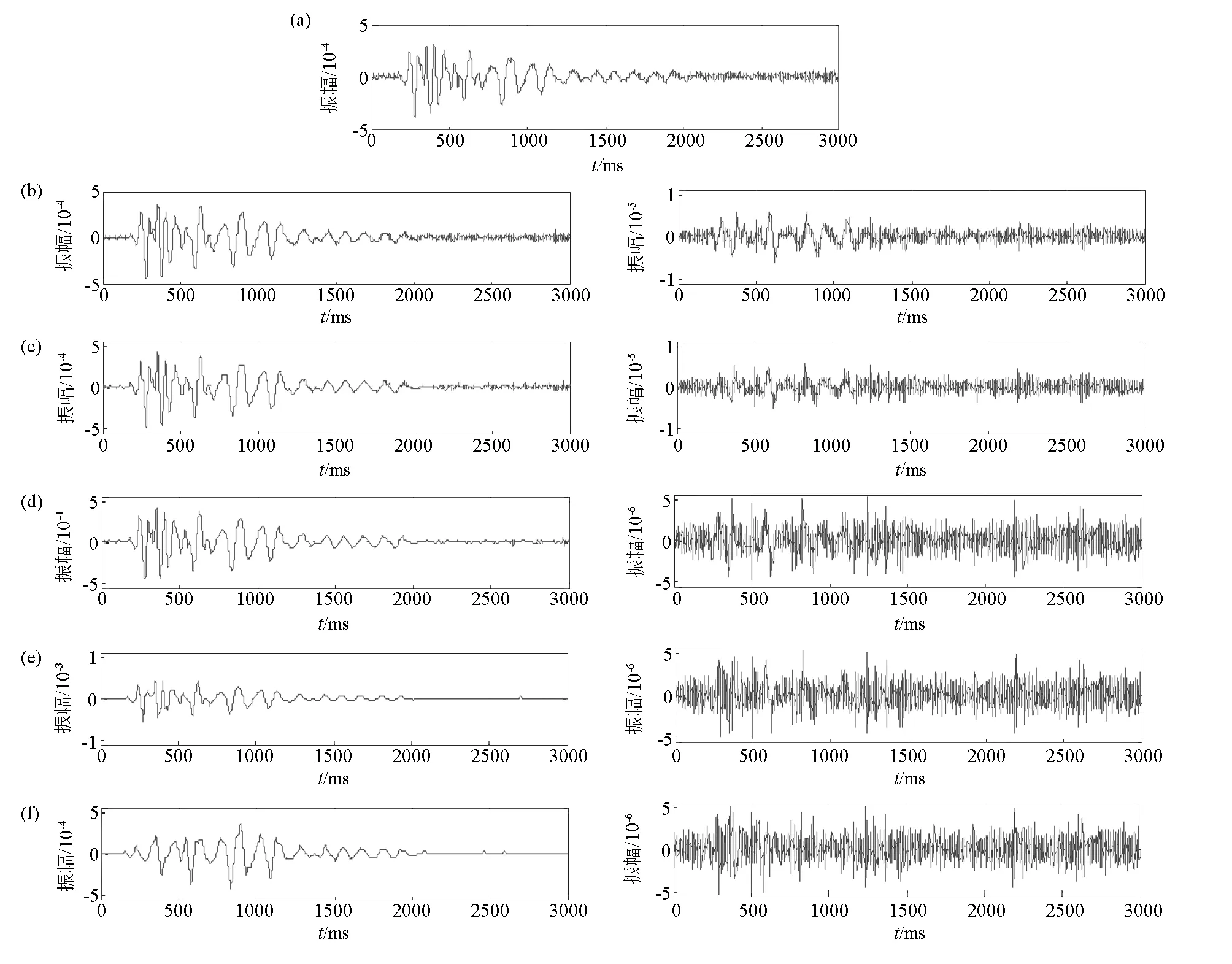
a—观测信号;b、c、d、e、f—分别为改进的阈值降噪算法进行1~5层分解降噪效果a—oberservation signal;b、c、d、e、f—the denoising results of improved threshold algorithm from the first to the fifth decomposition
3 实际地震数据降噪处理
为了显示改进的阈值方法降噪效果,将其应用到实际地震数据降噪处理应用,数据来源于中国地质调查局计划项目“深部找矿复电阻率法技术研究”,该炮记录共有584道,采样点6 000,采样率为1 ms,原始地震记录如图5a所示。由图5a可知,存在大量随机噪声,各道间数据相关性较差,几乎看不出地震数据记录的双曲线特征。通过本文提出的改进阈值算法以及软、硬阈值函数对原始地震数据(图5a)中的干扰噪声进行消除。通过前面分析,选取sym3为降噪的小波基和3层小波分解。通过软阈值函数降噪后的结果如图5b,硬阈值函数降噪后的结果如图5c。由图5b、5c可知,大部分随机噪声得到了消除,地震数据记录的双曲线特征较为明显,然而,整个地震数据记录仍然存在大量的噪声干扰,说明软、硬阈值函数降噪效果不理想。最后将本文设计的改进的小波阈值函数直接对图5a中的数据进行降噪处理,降噪后的地震数据记录剖面如图5d所示,由图5d可知,降噪后的地震数据记录的双曲线特征十分明显,几乎没有噪声干扰。可见,本文提出的改进的小波阈值降噪算法降噪能力强,降噪效果优于软、硬阈值函数降噪。
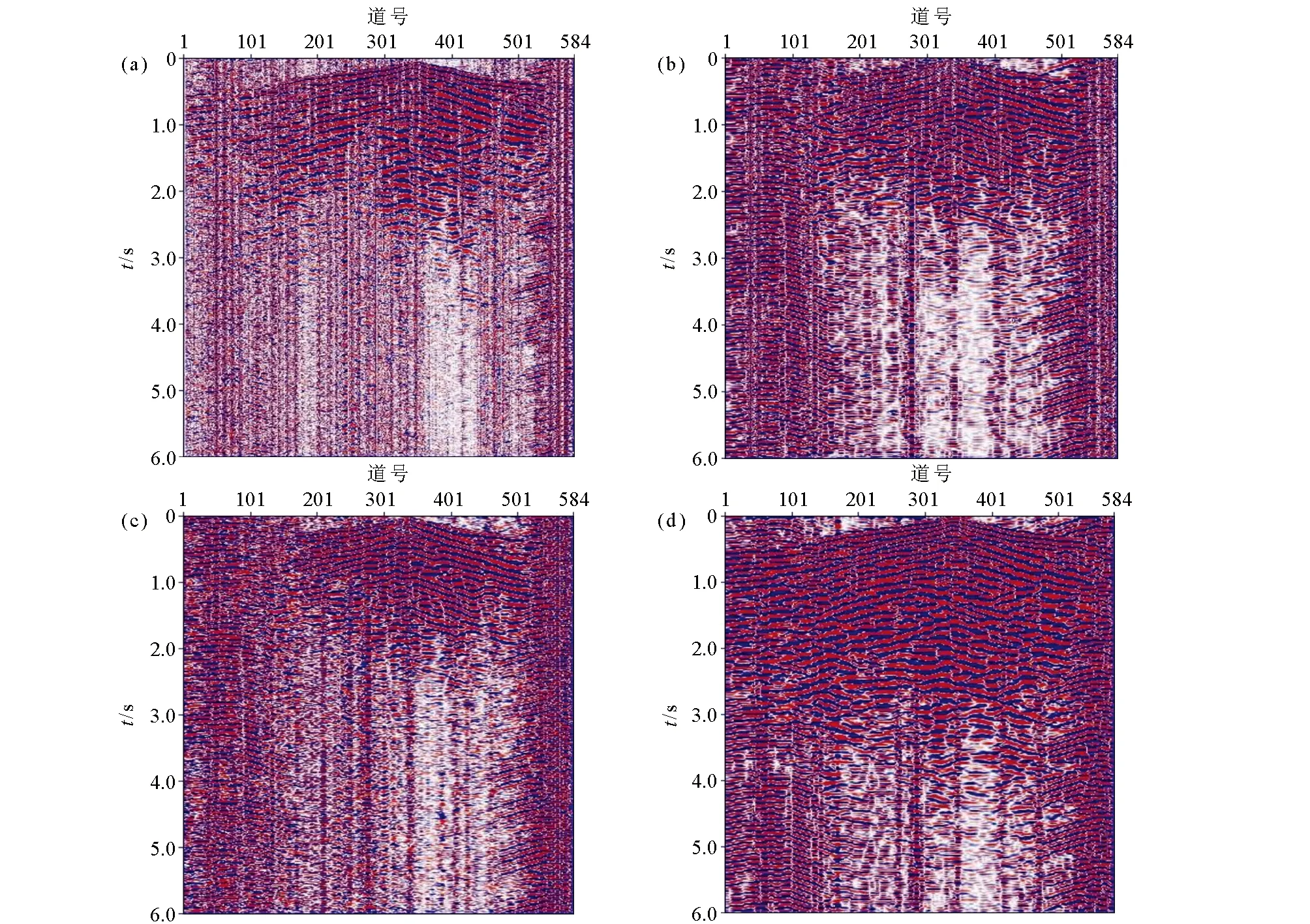
a—原始观察数据;b—软阈值函数降噪结果;c—硬阈值函数降噪结果;d—改进的阈值函数降噪结果a—original seismic data;b—denoising results of the soft threshold function;c—denoising results of the hard threshold function;d—denoising results of the improved threshold function
4 结论
1)文章在软、硬阈值函数基础提出了一种改进的小波阈值函数,并且具备软、硬阈值降函数特点,还避免了它们在信号降噪上的不足。
2)利用信噪比方法,均方根误差方法,结合仿真实验得出改进的小波阈值函数最佳小波基为sym3,最佳小波分解层数为3层。
3)改进的小波阈值函数在实际地震数据降噪处理中,其降噪能力较软、硬阈值函数降噪能力更强,它能够去除掉地震数据记录的噪声干扰,降噪后的地震记录剖面分辨率高。
