FeSiBPCu非晶合金磁性的EET理论计算

郭轩轩，吴萧雨，罗志群，张于顺，谷 月，李胜利，李 雪

（1辽宁科技大学 材料与冶金学院，辽宁 鞍山 114051；2辽宁科技大学 理学院，辽宁 鞍山 114051）

铁基非晶合金具有非常优异的软磁性能［1-2］，矫顽力低，饱和磁感应强度和磁导率高，通常被用于变压器的铁芯、滤光器以及其他电子领域［3-4］。用于制作变压器内部的铁芯时，与传统的硅钢、坡莫合金等相比，空载耗损可降低60%～80%［5］，符合节能环保的要求，是一种绿色节能材料，使用量逐年增长。我国自上世纪七十年代起，开始自主探索铁基非晶合金领域［6］，现在已经突破万吨级铁基非晶带材生产大关，并且在生产应用上领先于一些发达国家［7］。

通过添加不同合金元素可以使非晶合金的非晶形成能、力学性能和磁性能等有所提高，在该方面的研究十分广泛［8］。但是，这类研究大多集中在宏观实验上，对于价电子结构层次的研究还很少，因此，理论计算显得尤为重要［9］。本文通过理论计算，利用固体与分子经验电子理论（Empirical electron theory，EET），特别是键距差法（Bond length difference，BLD）对（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金的磁矩进行了简单计算，在电子层次上对非晶合金软磁性能进行研究。

1 非晶合金制备实验

采用熔体旋淬法制备（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金。原料为高纯度的颗粒状Fe（质量分数99.95%）、块状Fe3P（质量分数99.5%）、块状Si（质量分数99.9%）、片状Cu（质量分数99.9%）以及块状B（质量分数99.9%），按照（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）的成分配制4种样品。在感应熔炼装置中，抽真空至2.5 mPa以下，实验过程中持续通入高纯氩气作为保护性气体，逐渐提高功率将所用原料充分熔化制得母合金锭，母合金锭破碎处理后通过液体急冷设备制得非晶合金条带。利用X射线衍射仪（XRD）和透射电镜（TEΜ）检测条带的非晶结构，采用振动样品磁强计（VSΜ）测定非晶合金的磁性能。

图1为（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金的XRD衍射图谱。衍射图谱中4种非晶合金条带均在44°左右出现明显的漫散射峰，没有其它晶体相的衍射峰。这表明所制得的4种条带均为非晶条带，没有晶体析出。

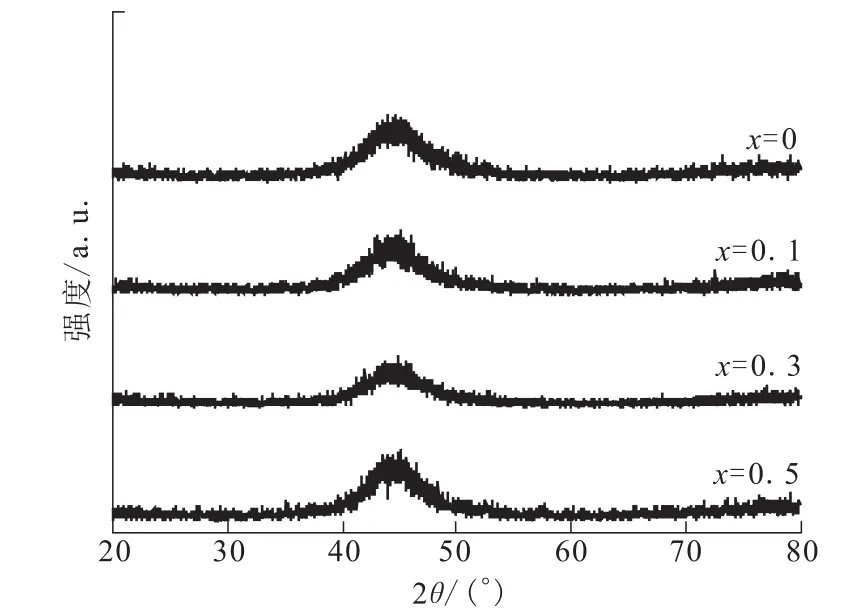
图1 四种非晶合金的XRD衍射图谱Fig.1 XRD diffraction patterns of four amorphous alloys

图2 是（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0.3）非晶合金的TEΜ形貌及选区电子衍射花样。衍射环为连续的晕环图样，且基体形貌无任何结晶结构特征，表明所制备的合金为完全非晶态结构。

图2 （Fe0.76Si0.096B0.084P0.06）100-xCux（x=0.3）非晶合金的TEΜ透射形貌及选区电子衍射花样Fig.2 TEΜ imageand SAEΜ of amorphous alloy（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0.3）

采用样品振动磁强计VSΜ测得（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金的磁矩值，分别为160.1、159.0、155.6和153.3 emu/g。

2 磁矩计算

2.1 价电子结构计算

根据EET理论，将非晶合金在微小区域内近似看成晶态结构［10］。推断在非晶合金（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）中与软磁性能相关的主要有4种晶胞［11］，分别为α-Fe、α-Fe-Si、α-Fe-B和Fe-P，其它可能存在的晶胞因数量少、没有磁性原子等因素对合金的软磁性能没有贡献，可忽略不计。α-Fe、α-Fe-Si、α-Fe-B和Fe-P晶胞的价电子结构计算模型参考文献［12］方法，分别计算出各晶胞的理论与实验键长，由两者的差值小于0.005 nm和软磁性能的相对误差在10%以内，作为量子态构定合理性的判据。

本文以α-Fe-Si晶胞为例，进行各相关物理量的计算。Si原子将α-Fe晶体中的部分Fe原子置换，新形成的α-Fe-Si晶体结构如图3所示，取α-Fe-Si的晶格常数为a=0.286 64 nm。

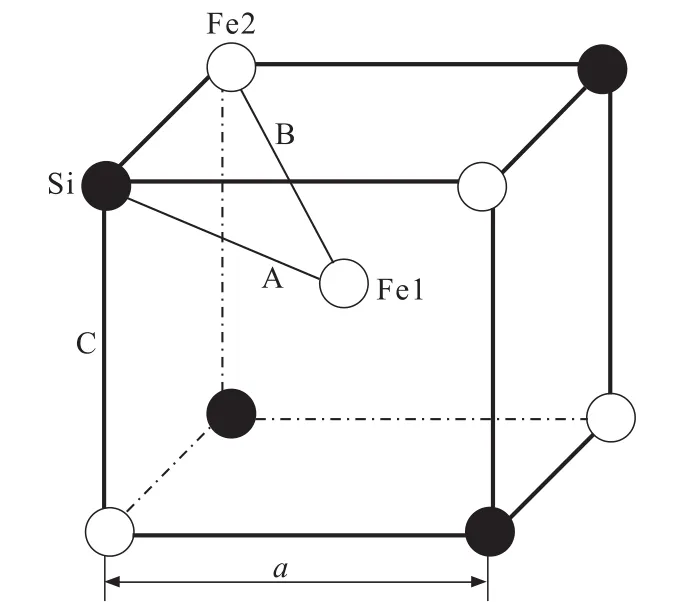
图3 α-Fe-Si晶体结构示意图Fig.3 Crystal structure of α-Fe-Si

（1）实验键距。α-Fe-Si晶胞中有四种不同的键，分别为Fe1-Si键、Fe1-Fe2键、Fe2-Si键以及Fe1-Fe1键，依次用A、B、C、D表示，其实验键距分别为

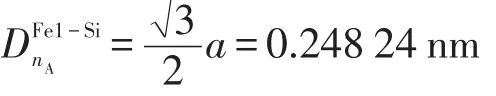
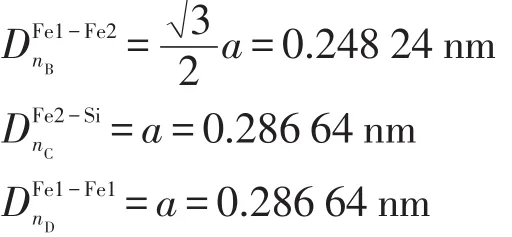
（2）等同键数

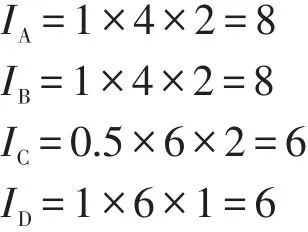
（3）键距方程和rα的计算

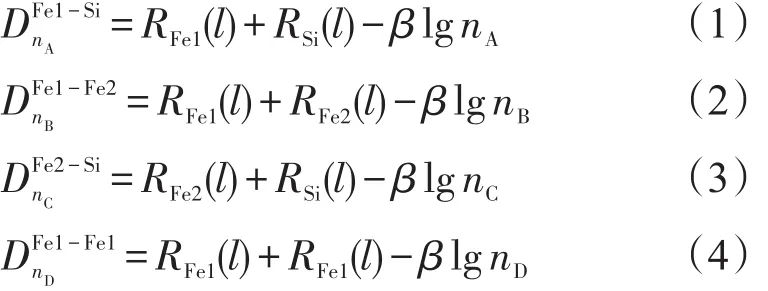
若体系是金属性的，则取β值为0.06 nm，若体系是非金属性的，则先取β为0.071 nm。Rn(l)为晶体结构中各原子对应的单键半距，可通过杂阶表查得。rα为在各个共价键上电子对数目的相对值。

将数据代入式（5）～式（7）中，计算得：rB=0.694 7，rC=0.214 8，rD=0.169 8。

（4）nA方程和共价电子对na的计算。在α-Fe-Si晶胞中，共有1个Fe1原子，0.5个Fe2原子和0.5个Si原子，EET理论中假设一个结构单元内所有原子的共价电子全部分布在共价键上，所以

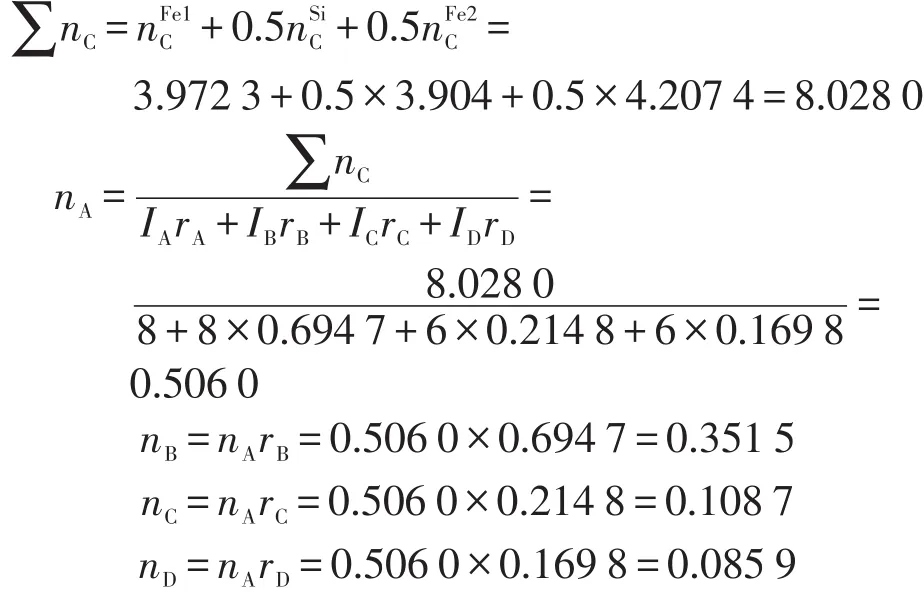
其中，rA=1。

（5）理论键距的计算

（6）键距差ΔDnA的计算

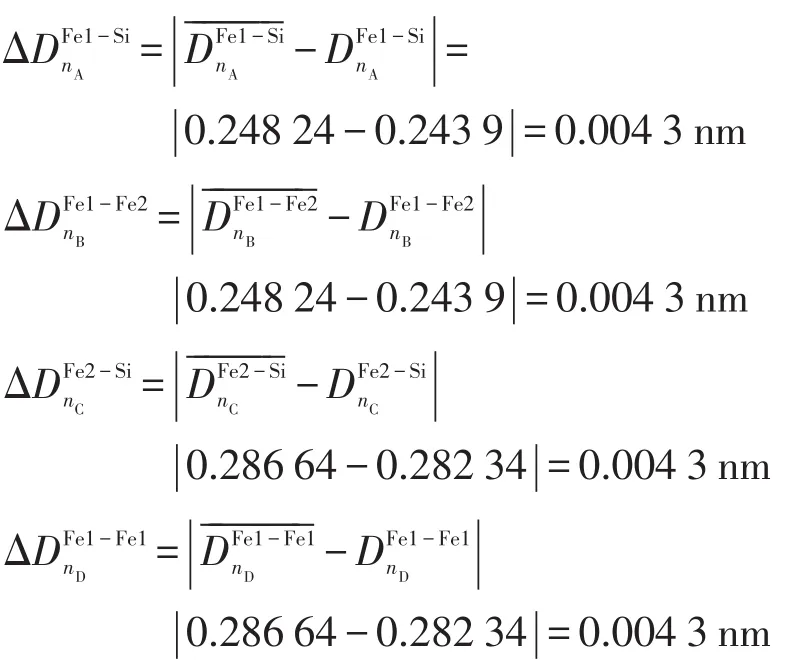
按照上述方法，分别对Fe和Si的杂阶进行计算，由于部分原子被替代，所以实际磁矩值偏小，并且考虑到计算所得键距差应满足量子态构定合理性的判据要求，所以取α-Fe-Si中的Fe1、Fe2、Si处于各原子杂化表的第10、11、5阶。

分别计算另外三种晶胞α-Fe、α-Fe-B、Fe-P的价电子结构，将四种晶胞各项物理参数记录于表1～表8中。其中，表1、3、5、7为各晶胞的相关计算所需参数由文献［13］查阅可得，表2、4、6、8为各晶胞计算所得参数。

表1 α-Fe晶胞计算所需参数［13］Tab.1 Calculation-required parameters of α-Fe unit cell[13]

表2 α-Fe晶胞计算所得参数Tab.2 Calculated parameters of α-Fe unit cell

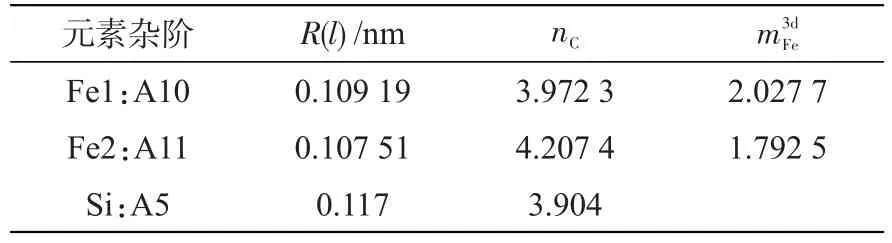
表3 α-Fe-Si晶胞计算所需参数［13］Tab.3 Calculation-required parameters of α-Fe-Siunit cell［13］

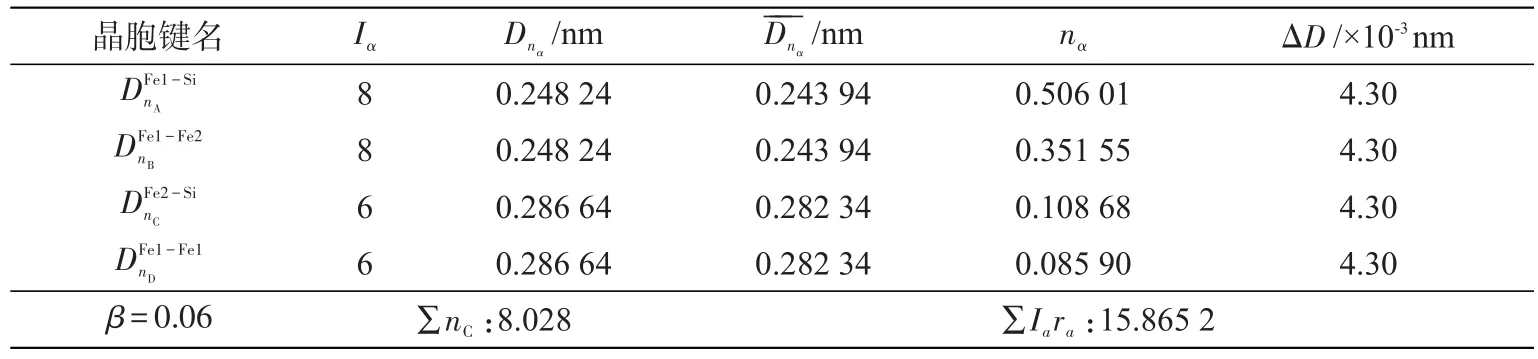
表4 α-Fe-Si晶胞计算所得参数Tab.4 Calculated parameters of α-Fe-Si unit cell

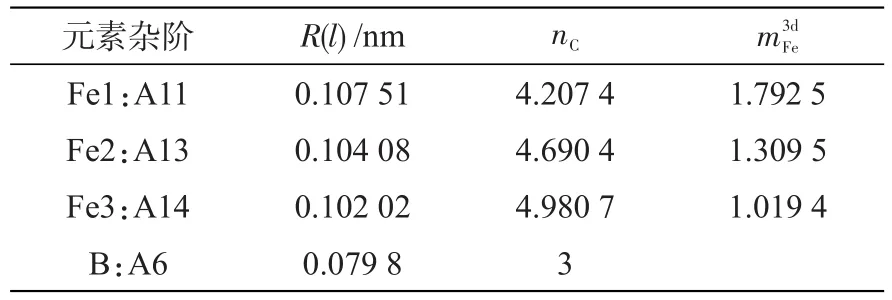
表5 α-Fe-B晶胞计算所需参数［13］Tab.5 Calculation-required parameters of α-Fe-B unit cell［13］

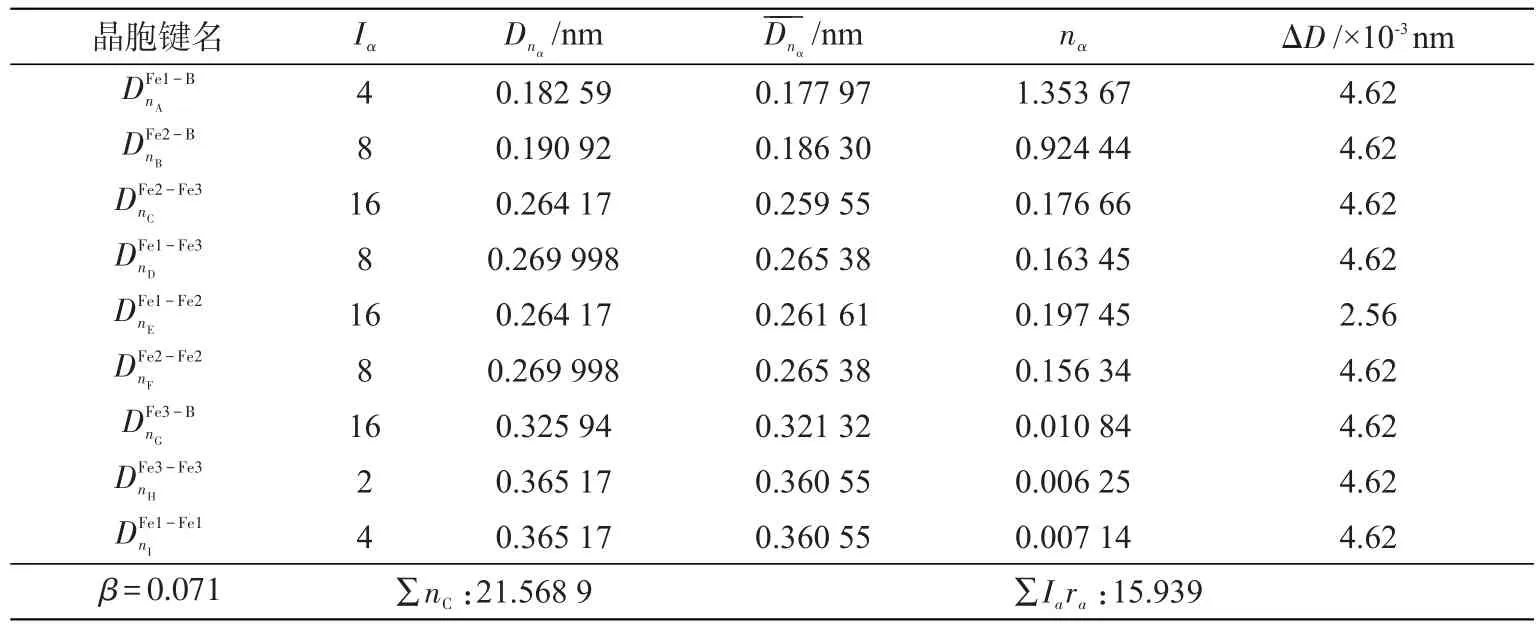
表6 α-Fe-B晶胞计算所得参数Tab.6 Calculated parameters of α-Fe-B unit cell

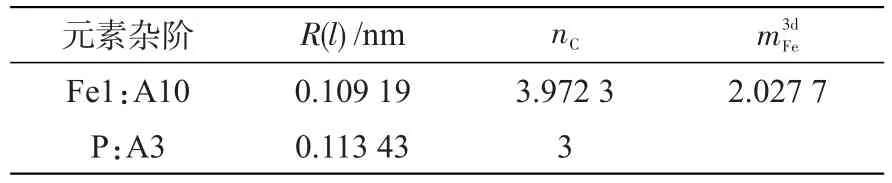
表7 Fe-P晶胞计算所需参数［13］Tab.7 Calculation-required parameters of Fe-P unit cell［13］

表8 Fe-P晶胞计算所得参数Tab.8 Calculated parameters of Fe-P unit cell

2.2 磁矩的理论计算

一个结构单元的总磁矩等于各原子磁矩之和。磁矩计算式

式中：g为朗德（Lande）因子，值为2.17。

一个α-Fe-Si晶胞的总磁矩值为

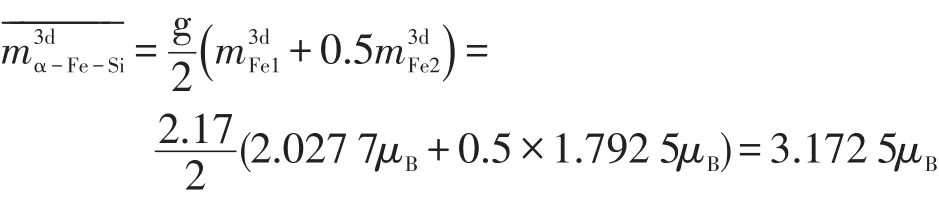
同理计算α-Fe、α-Fe-Si、Fe-P和α-Fe-B种晶胞的总磁矩分别为：4.157×10-20、2.942×10-20、5.462×10-20、2.040×10-20emu。

由Fe、Si、B、P四种元素在合金体系中的比例，确定上述4种晶胞在（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金中的数量，采用加权平均的方式，计算出合金的总磁矩值。以x=0的Fe76Si9.6B8.4P6非晶合金为例，设合金中有100个原子，则其中Fe、Si、B、P原子个数分别为76、9.6、8.4和4.8个。Fe、Si、B、P中只有Fe原子为磁性原子，且组成的晶胞中只有Fe原子对晶胞的磁矩有贡献，故只考虑以上四种晶胞。四种晶胞中只有α-Fe-Si晶胞中含有Si原子，并且每个晶胞中含有0.5个Si原子，故应该有19.2个α-Fe-Si晶胞，同理可得α-Fe-B晶胞共有8.4个，Fe-P晶胞共有6个，α-Fe晶胞共有3.8个。计算得1个Fe76Si9.6B8.4P6所包含的总磁矩为

因此，1 g淬态非晶合金Fe76Si9.6B8.4P6的总磁矩为

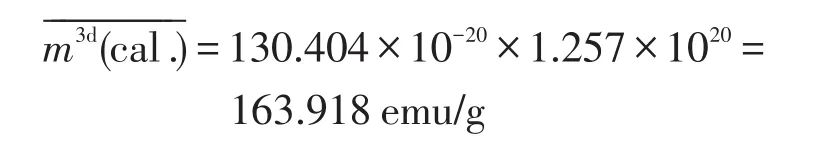
同理，得x=0.1、x=0.3和x=0.5的非晶合金（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）的总磁矩，详见表9。

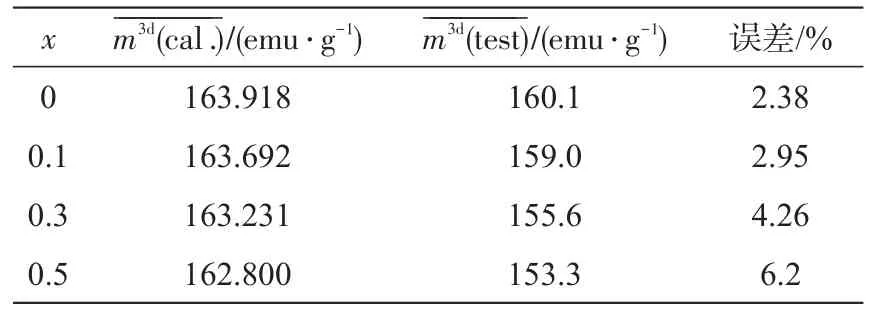
表9 （Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）非晶合金的磁矩及误差Tab.9 Μagnetic moments and error of amorphous alloys（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）

非晶合金（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）的磁矩随着x的增加而逐渐减小，实验值的变化趋势与此相同。这是由于随着Cu原子含量的增加，合金体系中磁性原子的占比减少，总磁矩减小。尽管Cu原子的加入会使非晶合金Fe76Si9.6B8.4P6的磁矩减小，但Cu元素对于纳米晶的析出有重要作用，故还需进一步研究Cu的加入对磁矩值的影响。通过计算得出的磁矩值与实验所得相差不超过10%，在合理范围内，说明从理论上计算非晶的磁矩是可行的，可以通过逆推的方式，根据所需非晶软磁性能得到其组成成分，设计出新的合金体系，为新的合金成分设计提供了一种新思路。

3 结论

（1）本文利用熔体旋淬法制得非晶合金（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）条带，且非晶合金条带具有较好的软磁性能，磁矩值分别为160.1、159.0、155.6和153.3 emu/g。

（2）利用固体与分子经验电子理论中的BLD方法，在价电子层次上实现了对非晶合金（Fe0.76Si0.096B0.084P0.06）100-xCux（x=0，0.1，0.3，0.5）磁矩的理论计算。磁矩的理论计算值与实验测定值的误差均在10%以内。