AGC综合调频性能指标计算方法

2020-07-25李志强王凡凯王克飞

河北电力技术 2020年3期

李志强,王凡凯,陈飞,王克飞

(北京华电天仁电力控制技术有限公司,北京 100039)

0 引言

AGC(Automatic Generation Control,自动发电控制)系统是指发电机组根据调度输出的负荷指令,自动调节机组出力以维持电网频率稳定[1]。发电主体可选择厂级AGC 模式或单机AGC 模式,区别在于前者是以全厂作为一个发电单元而后者是以单机作为一个发电单元参与调频市场[2]。根据《新能源产业振兴规划》草案,国内将建设7个千万级风力发电系统[3],到2020年将新增约15 000万k W 的风电装机容量,电网调频压力将逐步加大,由火电企业承担的调频任务越来越重[4]。另外以广东电网调频为例,电网负荷水平高峰时达1 亿k W,且峰谷差大,约3 500 万k W;部分时段变化速率较大,达80 万k W/min。随着现货市场的逐步开展,调频将从“事前调节”为主转为“事后平衡”为主,负荷快速变化时段的偏差量,按照目前的机组性能更加无法满足安全运行要求,需继续优化机组性能或引入快速调频电源。

综上我国调频市场未来的需求将进一步增大,吸引更多新兴技术参与到电力调频服务中来,而任何技术的应用都需要在规划时对其效果进行精准评估,因此,k 值的准确计算对于制定控制策略、考察运行效果以及分析系统收益都尤为重要。

有文章[5-7]从理论上对“两个细则”中k 值的计算方法予以解释,但并未分析火电机组在实际运行中不能准确完成AGC调节的特殊情况,也未给出如何在算法中实现多种运行状况的实时识别与处理,计算过程存在局限性,而本文将对这些特殊情况进行分析并给出详细的计算处理方法,提高指标计算精度。

1 AGC调节曲线分析

2017年11月13日,南方能源市场监管局发布《关于组织开展广东调频辅助服务市场模拟运行的通知》,规定AGC 综合调频性能指标k 的计算公式如下:

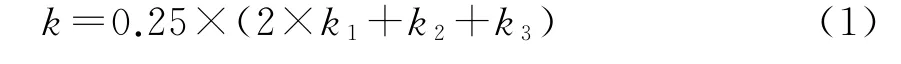
式中:k1为调节速率;k2为响应时间;k3为调节精度[8]。升负荷调节与降负荷调节同理,这里仅就升负荷调节过程进行详述。如图1所示。

图1 AGC调节曲线

基本一个AGC 调节周期为t0至t3间隔内,当下一个AGC 指令到来时刻即t3点,计算得出前一次调节性能指标k 值。

a.判断AGC指令到来,记录AGC 到来时刻Point,满足公式2:

式中:AGC 为实时值;AGC0为前一个AGC指令值。

b.记录AGC指令到来时刻机组出力值。

c.累计AGC指令个数N,获得AGC 调节周期个数N-1。

d.判断AGC-AGC 0 的正负。若AGCAGC 0为正,则为升负荷指令,记录升负荷指令时间点。

e.将发电机组出力可靠的跨出P0死区的时间点作为发电机组开始响应AGC 调节指令时间点t1。即在当前AGC调节周期内,机组在该周期内最后一次满足公式(3)时,记录上升响应时间点t1,以及此时的机组上升响应功率P1。

式中:P 为机组实时出力值;Siqu 为机组调节死区值,一般为机组额定功率的0.5%。

这里以机组跨出机组出力值的死区为准,而非跨出前一周期AGC指令值死区,是因为存在特殊情况,如图2所示。

图2 机组出力欠调/超调的情况

AGC第二个指令到来时刻机组出力并未完成前一次AGC指令的调节,存在过调或欠调的情况,机组出力与AGC 目标值并不相等,因此不能准确反映机组速率。

t2为机组出力达到调节死区的时间点,即机组结束调节时刻,机组在该周期内最后一次满足公式(4)时,记录上升结束时间点t2,以及此刻的机组上升结束功率P2,t2之后直到下一个AGC指令到来之前,机组出力始终在该调节死区之内:

其中存在特殊情况:如图3所示,机组出现降负荷调节时,也可能满足公式(4),因此需要附加升负荷判断约束公式(5):

图3 机组降负荷调频

2 调频性能指标计算分析

2.1 调节速率k 1

k1指发电单元响应AGC 控制指令的速率[9],k1=发电单元实测速率/控制区内AGC 发电单元平均标准调节速率(p.u.)。

为避免机组发电单元响应AGC 控制指令时过调节或超调节,k1最大值暂不超过5。由于k1值与当前AGC调节周期结束时刻无关,因此获得t2以及P2值后,可直接计算得到k1值,k1最大值暂不超过5,具体计算方法如公式(6):

式中:Pb为标准调节速率,燃煤机组是机组额定容量的1.5%/min[10]。

但存在两种特殊情况,如图4所示。

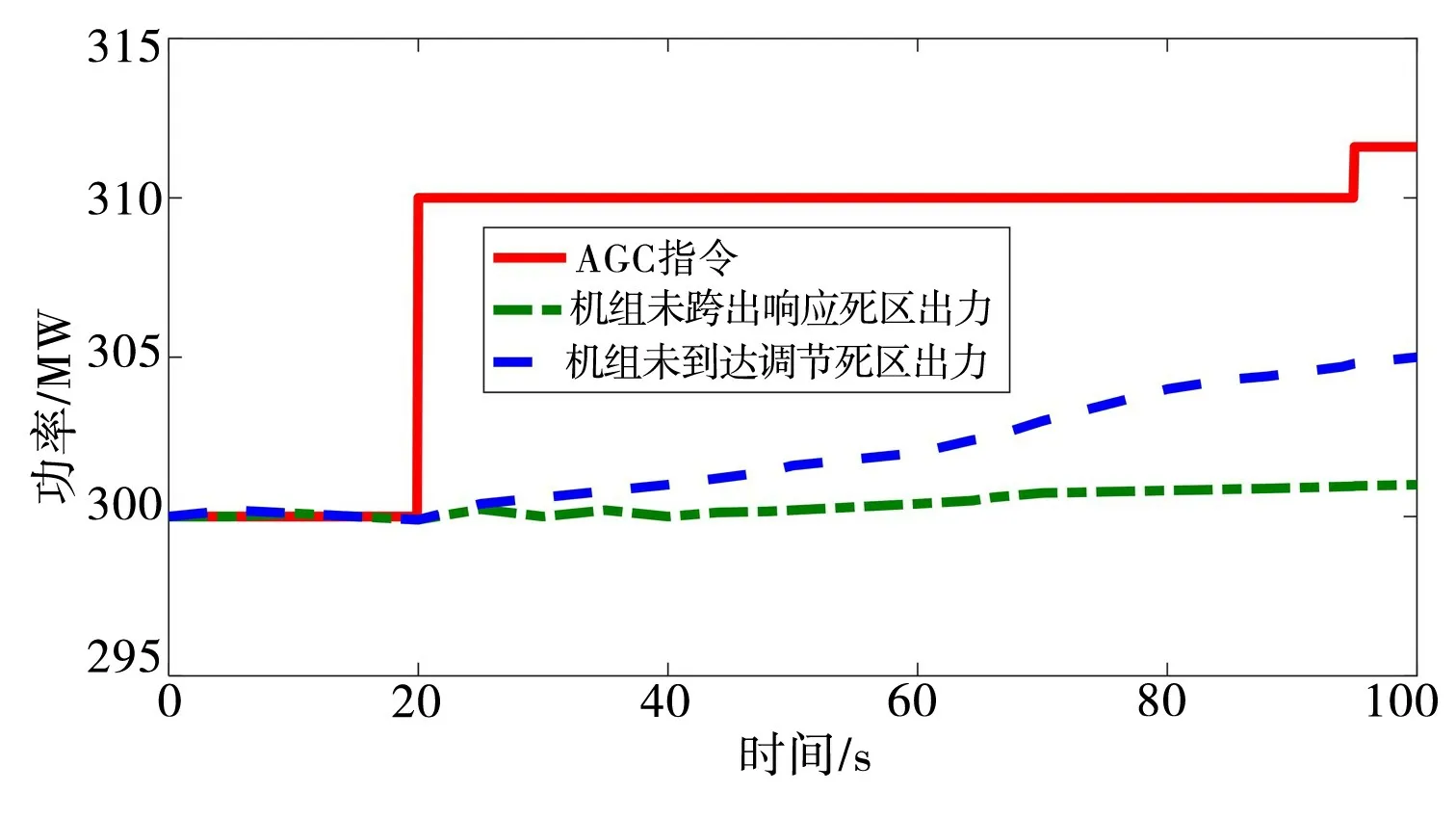
图4 机组出力未完整AGC调节任务

a.某一调节周期内,机组出力始终未能跨出响应死区。此次AGC 调节过程中不满足公式(3),无法通过计算得到t1与P1的值,该变量值仍为前一次调节时获得的数据值,不能用来反映此次调节情况,因此赋值此次调节k1=0。

b.某一调节周期内,机组出力虽然已跨出响应死区,但并未到达调节死区内,此次AGC 调节过程中不满足公式(4),无法获得t2,P2值,因此赋值此次调节k1为0。

2.2 响应时间k 2

k2指发电单元响应AGC控制指令的时间延迟,k2=1-(发电单元响应延迟时间/5 min)。

其中,发电单元响应延迟时间是指发电单元AGC 动作与发电单元接到AGC 命令的延迟时间[11]。实际计算时,通常以机组出力可靠的跨出机组出力响应死区时的时刻值,减去该调节周期内AGC指令到达时刻的差值作为延迟时间。k2具体计算方法如公式(7):

当系统运行情况出现图4中的出力未跨出响应死区的情况时,则k2=0。

2.3 调节精度k 3

k3指发电单元机组响应AGC 控制指令的精准度,k3=1-(发电单元调节误差/发电单元调节允许误差)。

其中,发电单元调节误差指发电单元响应AGC控制指令后实际出力值与控制指令值的偏差量,发电单元调节允许误差为其额定出力的1.5%。

对于实时连续时间序列,要计算t2至Point之间AGC与P差值的积分,方法如下:

当到达Point时刻时,触发输出J1:

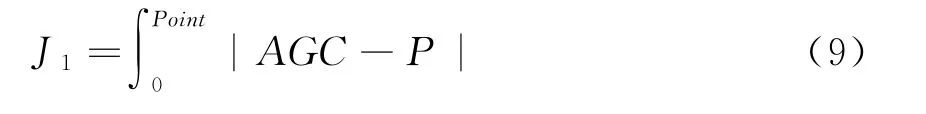
k3具体计算方法如公式(8),Pn 为机组额定功率[11]:

当系统运行情况如图4所示时,机组未到达调节死区,则k3=0,此时k=0.25×k2。

3 算法模块封装

AGC计算模型的算法流程如图5所示。

图5 算法流程

通过采用Matlab提供自定义需求模型的接口函数S-Function编写k 值算法,并为该算法模型定制可视化的操作界面,如图6所示。该模型可根据需要定义k 值计算的起始点,以获得某一时间段内的k 平均值。通过累计某段时间内的升负荷与降负荷调节k 值之和取平均实现。

图6 k值计算模型

4 计算实例

广东省某电厂由于其机组本身性能的劣势导致AGC调节效果差,辅助服务中标率低,因此考虑联合储能以提升电厂的AGC调节性能。

取电厂装机容量为350 MW 的2号机组2018年2月份连续15日内的综合调频性能指标k 值数据绘制图7,计算得平均k 值为0.589 8。

图7 实际机组的综合调频性能指标曲线

a.分别建立锅炉、DEH、汽轮机、发电机各部分模型构成火电机组[12],取机组2018年2月22日16:06:40 至18:19:59,共计7 980 s时长的AGC数据与机组出力数据,给定机组模型同样的AGC指令,获得的响应曲线如图8所示。

图8 机组模型AGC响应曲线

选取判定系数R-square,它是度量拟合优度的一个统计量,可以判定两条曲线的相关度。大小区间为[0,1],指标越接近1,曲线相关度越高:

其中SSE(和方差):该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式为[13]:

式中:wi为权重系数,这里取值为1。

SST 为原始数据和均值之差的平方和[14],公式为:

计算得出,模型得到的机组响应曲线和现场机组响应曲线相关度为:R-square=0.983 4,模型准确度较高。

b.建立储能系统仿真模型,包含电池、DC/AC逆变器、滤波器、控制器等部分。储能系统的功率在实际工程项目中一般按照机组装机容量的3%配置,满功率放电时间持续0.5 h,因此本例中储能系统配置为10 MW/5 MWh。

系统控制采用电压外环电流内环的双环PI控制方案。电流内环可扩大逆变器控制系统的带宽,使得逆变器动态响应加快,输出电压的谐波含量减小,非线性负载适应能力加强[15]。控制参数采用粒子群算法进行优化。先优化电流内环参数,再优化电压外环参数。目标函数如公式(14)所示:

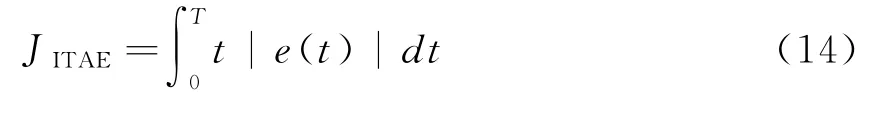
优化算法流程如图9所示。

图9 粒子群优化算法流程

最终优化结束得到控制参数如表1所示。

表1 控制参数优化结果

c.储能系统与机组模型构成联合调频系统,如图10所示,储能逆变器交流侧输出为380 V 电压,经过变压器升压并入6.3 k V 高厂变低压侧,模拟储能辅助火电机组运行过程,不影响机组原本的运行。

图10 火储联合调频系统模型

以AGC与机组差值作为储能系统的输入,系统运行曲线如图11所示。

图11 机组联合储能AGC响应曲线

计算电厂加入储能前后AGC综合性能指标,取其中几个AGC调节周期详细数据见表2。

表2 k值计算结果

未加入储能时,机组模型综合调频指标k 值均值为0.572 9,实际机组k 均值为0.589 8,由于机组模型拟合度达到0.983 4,说明本文所述的k值计算方法精确度较高,误差小于0.02。而加入储能后,在不超过储能调节能力的前提下,k 值达到2.9,帮助机组快速跨出响应死区并完成AGC调节,大大提升了系统的AGC综合调频性能。