低信噪比地震资料初至自动拾取技术
2020-07-25蔡存军毛锐强彭志文万应明马永建
蔡存军,毛锐强,彭志文,万应明,王 龙,马永建
(1.中石化石油工程地球物理有限公司华北分公司,河南郑州450018;2.中石化海洋石油工程有限公司上海物探分公司,上海201208)
实践表明,基于初至波的模型静校正技术(折射反演静校正和层析反演静校正)与剩余静校正技术是解决地形起伏变化大、近地表结构复杂地区(比如沙漠、山地、山前带和巨厚黄土塬等地区)静校正问题的有效方法[1-2]。地震波初至拾取的精度与效率是影响该类静校正技术应用的关键。目前,人机交互式半自动初至拾取技术应用广泛,该技术能够保证初至拾取的精度,但需要大量的人工参与,耗时耗力。随着油田勘探开发的不断深入,新的地震勘探技术的不断发展,特别是当前高分辨率、高精度和全三维高密度地震采集技术的发展[3],地震数据量不断增大,单炮接收道数增多,人机交互式半自动初至拾取技术已经不能满足当前大数据量地震资料处理的需要。
近年来,地球物理学家们研究开发了多种初至自动拾取方法。有基于地震记录瞬时特征的方法,如分形维[4-5]、Akaike信息准则法[6]、二分法[7]和边缘检测[8]等,此类方法应用于高信噪比地震资料的效果较好,而对于低信噪比地震资料,因受噪声的干扰,难以准确拾取初至。有基于地震道初至时窗地震属性特征的方法,如能量比法[9]、振幅比法[10]及局部相似属性[11]等,这类方法由于受初至前噪声的干扰或者“续至波”的影响,导致在初至拾取过程中出现错拾或者漏拾。也有基于神经网络的方法,此类方法首先需要训练出样本数据,还需要选取适当的地震属性。宋建国等[12]提出改进的神经网络级联相关算法,该算法更加稳定,适应能力更强。潘军等[13]针对低信噪比浅水区OBS资料提出了三步法初至拾取方法,取得了很好的效果。胡瑞卿等[14]提出了基于自适应Morlet小波的初至拾取方法解决低信噪比微震资料初至拾取困难的问题。唐杰等[15]提出基于多尺度分解的微震噪声压制与初至拾取方法提高信噪比很低的微震数据初至拾取精度。梁上林等[16]基于稳相叠加原理,利用超级虚折射干涉加强弱的初至信号,加强了远偏移距处的弱初至能量,为后续拾取初至输入了信噪比高的数据。YUAN等[17]基于卷积神经网络提出了一种有效的全数据驱动的初至拾取方法。HU等[18]基于U型卷积网络提出了一种只需学习少量标记样本即可提高在复杂资料中初至拾取精度。JIA等[19]利用卷积神经网络衰减震源数据中“振铃效应”并拓宽频带,在此基础上利用时窗能量比法有效提高了震源数据初至拾取精度。王静波等[20]提出的基于改进多道局部复值相关的地震信号边缘检测技术,有效地增强了地震信息边缘异常检测和抗噪的能力。
初至拾取就是要对能量较弱的背景噪声与能量较强的初至波的边界进行区分,而数据中较低的信噪比势必会影响其边界的区分。本文提出了一种地震波初至自动拾取方法,该方法首先对单炮记录进行检波点高程静校正和线性动校正,然后利用曲波变换对校正后的数据进行噪声压制,最后利用改进的瞬时强度比法自动拾取初至,并利用模型数据和实际资料验证了本文方法的有效性。
1 技术方法
1.1 曲波(Curvelet)变换
1.1.1 曲波变换原理
曲波变换作为一种包含尺度参数和方位参数的多尺度变换方法,具有很好的方向性,能够对地震信号中包括直线、曲线和边缘等简单构造进行表征,并且由于曲波变换的曲面表征特性,使其更适合描述地震波的波前特征。地震数据经过曲波变换后,有效信号的曲波系数呈规则分布,而随机噪声的曲波系数则随机分布[21-24],因此可以利用曲波变换压制随机噪声,且能够较好地保护有效信号的特征,提高地震资料的信噪比。如不做特殊说明,文中所述去噪指利用曲波变换法压制随机噪声。函数f(t1,t2)∈L2的离散曲波变换定义为:
(1)
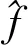
信噪比定义为:
(2)
式中:srms为有效信号的均方根振幅;nrms为噪声的均方根振幅。
图1给出了不同信噪比的合成记录(有效信号是振幅为1的简单脉冲信号)。由图可看出,图1a的信噪比相当低,几乎很难看到有效信号;图1b的信噪比相对较高,能看到0.2s处的有效信号;图1c的信噪比很高,能够清晰地看到0.2s处的有效信号;图1d是不含噪声的合成记录。
图2是图1所示不同信噪比合成记录的曲波系数分布。图2d中无噪声的合成记录经过曲波变换后,其系数在曲波域内分布于有限区域内,白色直线即为有效信号;图2c中有效信号的曲波系数在曲波域内分布位置与图2d中相同且幅值相对较大,在其它各区域可看到幅值相对较小且零星分布的随机噪声系数;图2b中有效信号曲波系数在曲波域内的位置依然与图2d中相同,随机噪声曲波系数在曲波域内各位置均有分布,其幅值相比图2c中有所增大,有效信号依然清晰;随着信噪比的降低,曲波域各区域分布的随机噪声曲波系数幅值逐渐增大,但仍然能够看到有效信号,且其位置没有变化,见图2a。
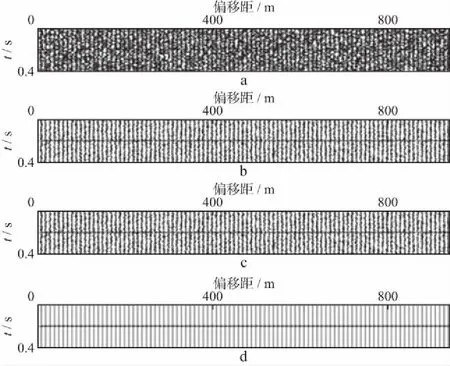
图1 不同信噪比合成记录a 信噪比0.15; b 信噪比0.45; c 信噪比0.75; d 无噪声

图2 不同信噪比模拟记录曲波系数分布a 信噪比为0.15; b 信噪比为0.45; c 信噪比为0.75; d 无噪声
当信噪比不同时,有效信号与随机噪声各自的曲波系数在曲波域内幅值是不同的。随着信噪比降低,在曲波域内,随机噪声与有效信号的曲波系数幅值比会增大。有效信号曲波系数在曲波域分布于相对有限的区域内,而随机噪声曲波系数则是随机的分布于每个尺度、方向及位置。故可以据此差异设置合理的阈值进行“压制”,然后利用曲波反变换得到压制噪声后的地震记录。
图3分别是未加入静校正量和随机噪声、加入随机噪声、加入静校正量及同时加入静校正量和随机噪声合成记录尺度为3、方向为4的曲波系数曲线,纵坐标表示曲波系数幅值。可以看出,图3a中初至波对应的曲波系数幅值相对较大,其它区域均为0(图中曲线“波峰”区域对应初至波的曲波系数);图3b是加入信噪比为0.45的随机噪声之后的曲波系数曲线,初至波曲波系数与随机噪声系数可明显区分,前者幅值相比后者大很多;图3c是加入随机且变化较为剧烈静校正量(最大静校正量为66ms)后合成记录的曲波系数曲线,初至波对应的曲波系数幅值相比其它区域大(其它区域为0),但与图3a相比,初至波曲波系数幅值小很多,造成这种现象的原因是初至不光滑而使初至曲波系数在曲波域内分布更分散;图3d 是同时加入静校正量和随机噪声之后的曲波系数曲线,初至波与随机噪声基本很难区分,只有少部分可以区分。说明当数据中同时存在剧烈变化的静校正量和随机噪声时,很有可能使得初至波和随机噪声在曲波域内不易区分。因此,有必要在去噪前先使单炮初至更为光滑,使初至波的曲波系数分布尽可能如图3b,更易区分初至信号与随机信号。
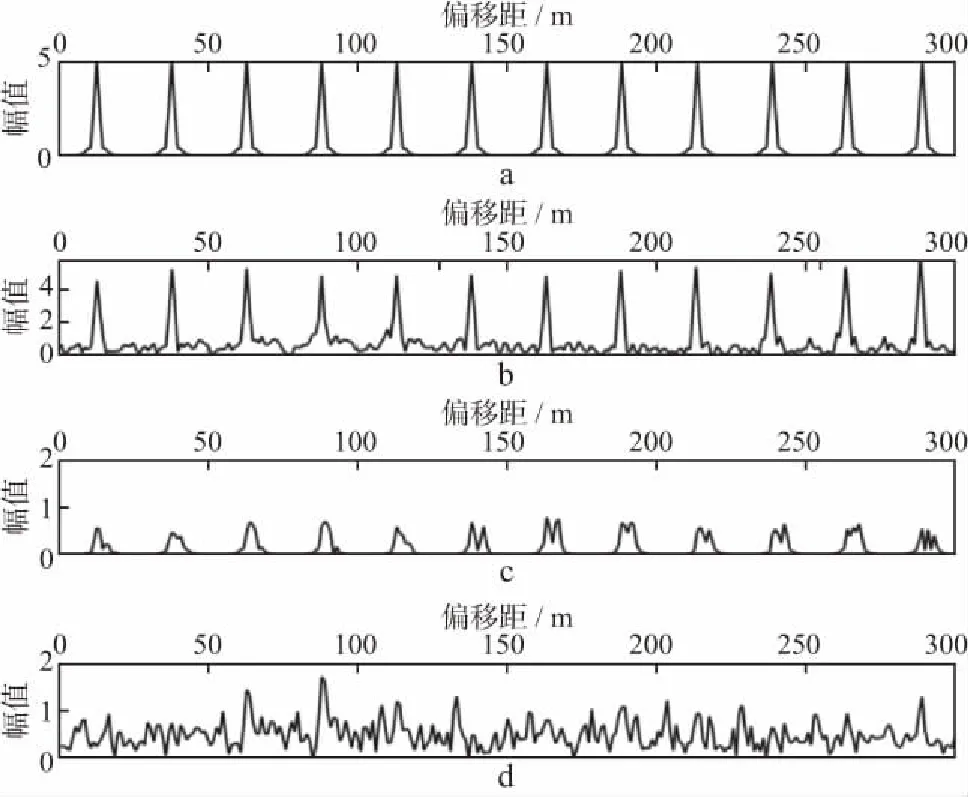
图3 合成记录在尺度3、方向4时的曲波系数曲线a 未加入静校正量和噪声; b 加入静校正量; c 加入随机噪声; d 同时加入静校正量和噪声
根据经验,在实际地震资料中,通常由于地形起伏变化较大,导致单炮中初至剧烈变化,而由低降速带横向变化导致的初至起伏相对较为平缓(不考虑黄土塬和沙漠资料中黄土和沙漠厚度的剧烈变化,因为可以通过选择合适的替换速度对黄土和沙漠厚度变化进行填充校正,经过校正之后,使初至变得较为平缓)。因此,在去噪之前可以利用检波点高程静校正对因地形起伏变化而导致的初至扭曲进行校正,使单炮中初至更光滑,进而使得初至波系数在曲波域内更集中,与噪声系数更易区分。
1.1.2 阈值及阈值函数选择
应用曲波变换法去噪的关键在于选择合适的阈值及阈值函数。在曲波域内,有效信号是稀疏的且可以由部分较大的系数值表示,而噪声可由大量存在的较小的系数值表示。在曲波域去噪通常采用统计意义上的阈值[25]。本文采用如下阈值[26]:
(3)
式中:j为尺度;σ为噪声标准差,可由σ={median{|C(j)-median[C(j)]|}/0.6745}2估算;N为输入数据的最大道数。
阈值函数有硬阈值函数、软阈值函数、软硬折中阈值函数及各种改进的阈值函数[25-27]。本文选用以下阈值函数:
C(j,l)=
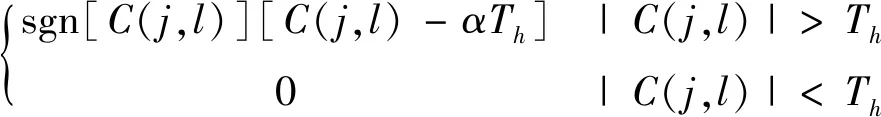
(4)
式中:α为调节参数,且0<α<1。当该值取0时则为硬阈值函数,该值取1时为软阈值函数。
1.1.3 曲波变换去噪
图4展示了应用曲波变换方法对模拟记录进行去噪的过程,该记录为简单数值模拟的记录,速度4500m/s,采样间隔4ms,子波主频25Hz,道距25m,总道数21道。图4a为模拟记录;图4b为加入高斯噪声的记录,信噪比0.35;图4c为去除随机噪声后的记录,其信噪比提高明显(图4c灰色方框中存在局部虚假信号,由曲波变换本身的伪吉布斯效应产生);图4d为去除的随机噪声。可见,应用曲波变换法可有效去除随机噪声,且去除的噪声中不含有效信号,对有效信号保护得较好。
尽管在去噪过程中较好地保护了有效信号,但是仔细对比图4a和图4c发现,两者并不完全一致,后者初至波振幅略小,且其附近波形存在局部“震荡”。这是去噪的必然结果,即会在一定程度上改变原始记录振幅、波形等特征。那么这种改变会对初至拾取造成多大程度的影响?这种影响是否在可接受的范围之内呢?本文重点关注瞬时振幅极大值对应的时间是否会发生改变且这种改变是否可以接受。
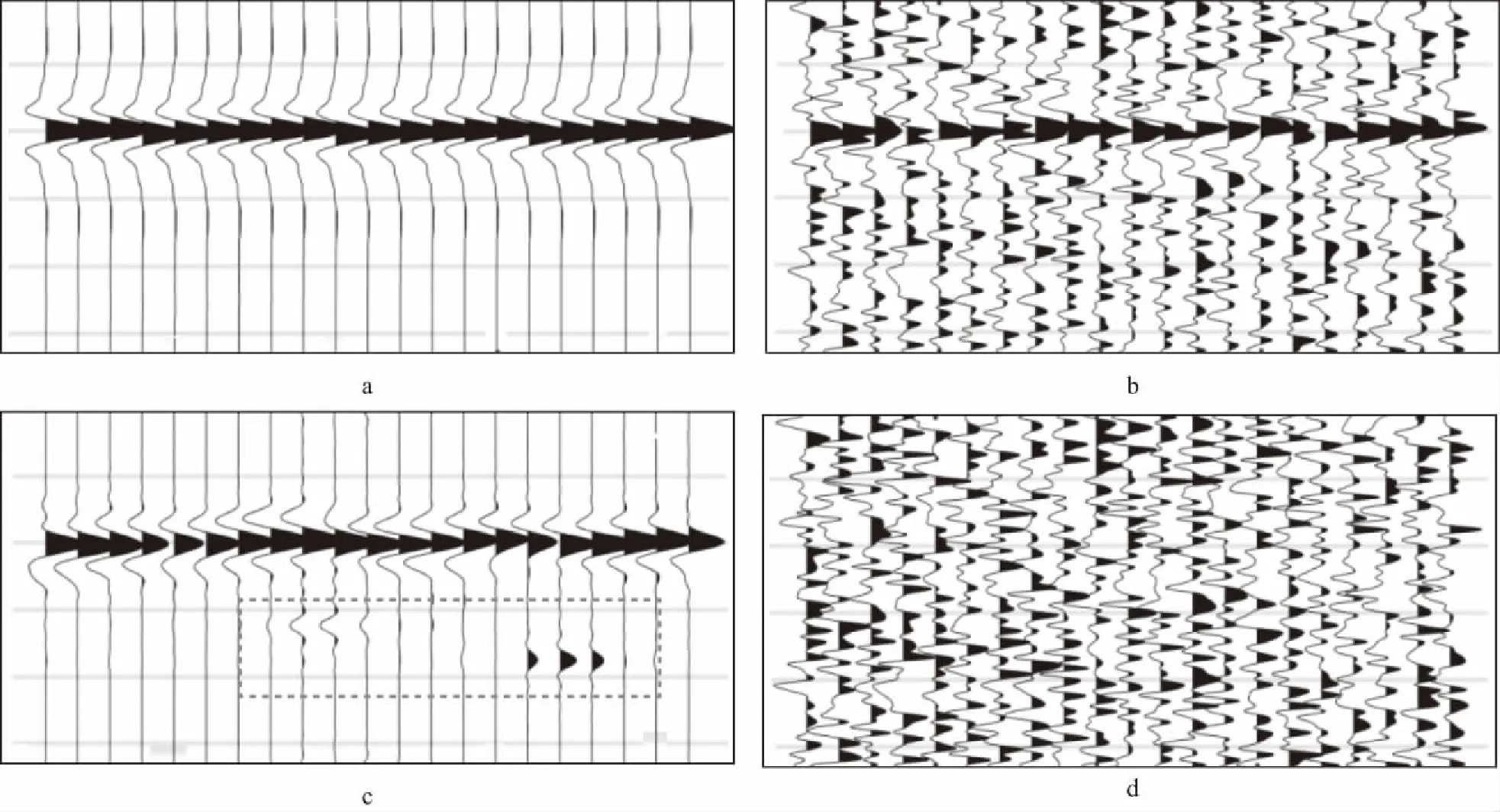
图4 应用曲波变换去噪a 模拟记录; b 加噪记录; c 去噪记录; d 去除的噪声
分别求取模型数据、加噪数据(信噪比0.35)及去噪数据的瞬时振幅(具体见1.2节)。图5中展示不同数据的瞬时振幅极大值的位置(即样点序列),黑色实线表示模型数据的瞬时振幅极大值的样点序列(均为26),红色点线表示去噪数据极大值的位置,在第5,6道与黑色实线差1个样点,其余道均重合,蓝色虚线表示加噪数据极大值的位置,除在第10,13,15,19道与黑色实线重合之外,其余各道均不与其重合,而且最大相差达5个样点。
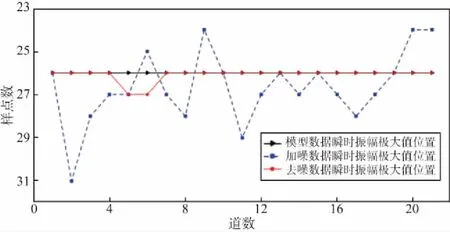
图5 不同数据瞬时振幅极大值位置
加入随机噪声之后,数据大部分瞬时振幅极大值位置发生了变化,且部分移动了5个采样点,这势必会对依赖于瞬时振幅特征的初至拾取产生较大的影响。而去噪后,只有个别道的瞬时振幅极大值位置发生了变化,且只移动了1个样点,这在可以接受的范围之内,即样点移动距离小于λ/4。去噪会在一定程度上改变原始数据的特征,但是只要这种改变在合理的范围内(即“温和”去噪原则),则可对初至进行去噪处理。
1.2 希尔伯特变换和瞬时振幅
通常采用复数道分析技术来提取包含瞬时振幅、瞬时频率、瞬时相位在内的地震瞬时属性。瞬时振幅在资料解释中应用广泛,用于振幅异常的品质分析,以检测断层、河道、地下矿床、薄层调谐效应及从复合波中分辨出厚层反射。张伟等[10]论述了采用基于希尔伯特变换的瞬时强度法,使初至波同相轴变得更加光滑,与滑动时窗能量法相比,其在拾取精度等方面效果更好。
对于一个实值函数x(t),其希尔伯特变换记作y(t)定义为:
(5)
式中:H表示希尔伯特变换。
地震复数道分析技术就是首先对地震记录x(t)进行希尔伯特变换得到y(t),然后将x(t)作为复数道的实部,将y(t)作为复数道的虚部,则时域地震复数道z(t)为:
z(t)=x(t)+iy(t)
(6)
z(t)可以看作是一个一维的地震信号变成二维复平面上的信号,复数的模和幅角代表了信号的幅度和相位,因此,地震道在经过复数变换后,可以很方便地从原始地震记录中得到瞬时振幅、瞬时相位。
复数地震道中任何位置处的瞬时振幅可以表达为:
(7)
瞬时相位表达为:
(8)
图6展示了由原始地震道x(t)计算其希尔伯特变换并构建复数地震道的过程。图6a为原始地震道x(t);图6b中紫色线为其希尔伯特变换y(t);图6c中红色虚线为根据公式(7)求取的原始地震记录x(t)的瞬时振幅A(t)。瞬时振幅的极值对应了初至波的能量。
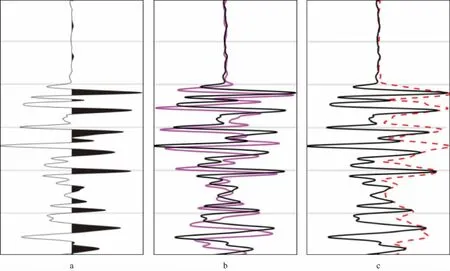
图6 地震道与其希尔伯特变换和瞬时振幅a 原始地震道x(t); b x(t)的希尔伯特变换y(t); c 瞬时振幅
1.3 初至拾取
1.3.1 瞬时强度比初至拾取
一般情况下,在初至波到达之前地震道的瞬时振幅很小,而初至到达之后地震道的瞬时振幅较大,因此地震道瞬时振幅比值会在初至到达前后有较大的变化。定义后时窗内与前时窗内瞬时振幅的平方和比值为瞬时强度比特征值(下文简称强度比)。通常,初至波处该比值最大,因此可以将强度比作为判定初至时间的依据。计算公式如下[10]:
(9)
式中:
其中:I为强度比;A(t)为瞬时振幅;T0为样点时间;T2为后时窗长度;T1为前时窗长度;D为一个地震道的瞬时强度;K为每一道内总的样点数;β是为了增强初至拾取的稳定性而加入的稳定因子,可以根据实际情况进行调整。
当地震资料信噪比较高时,根据公式(9)计算的强度比可以拾取到正确的初至。图7a是截取的某单炮记录中道号为35的一段地震道;图7b是对应各采样点处的强度比。可以看出,图7b中强度比最大值对应了图7a中的初至时间,即采样点数67(用红色箭头分别标记了单炮初至和强度比最大值)。
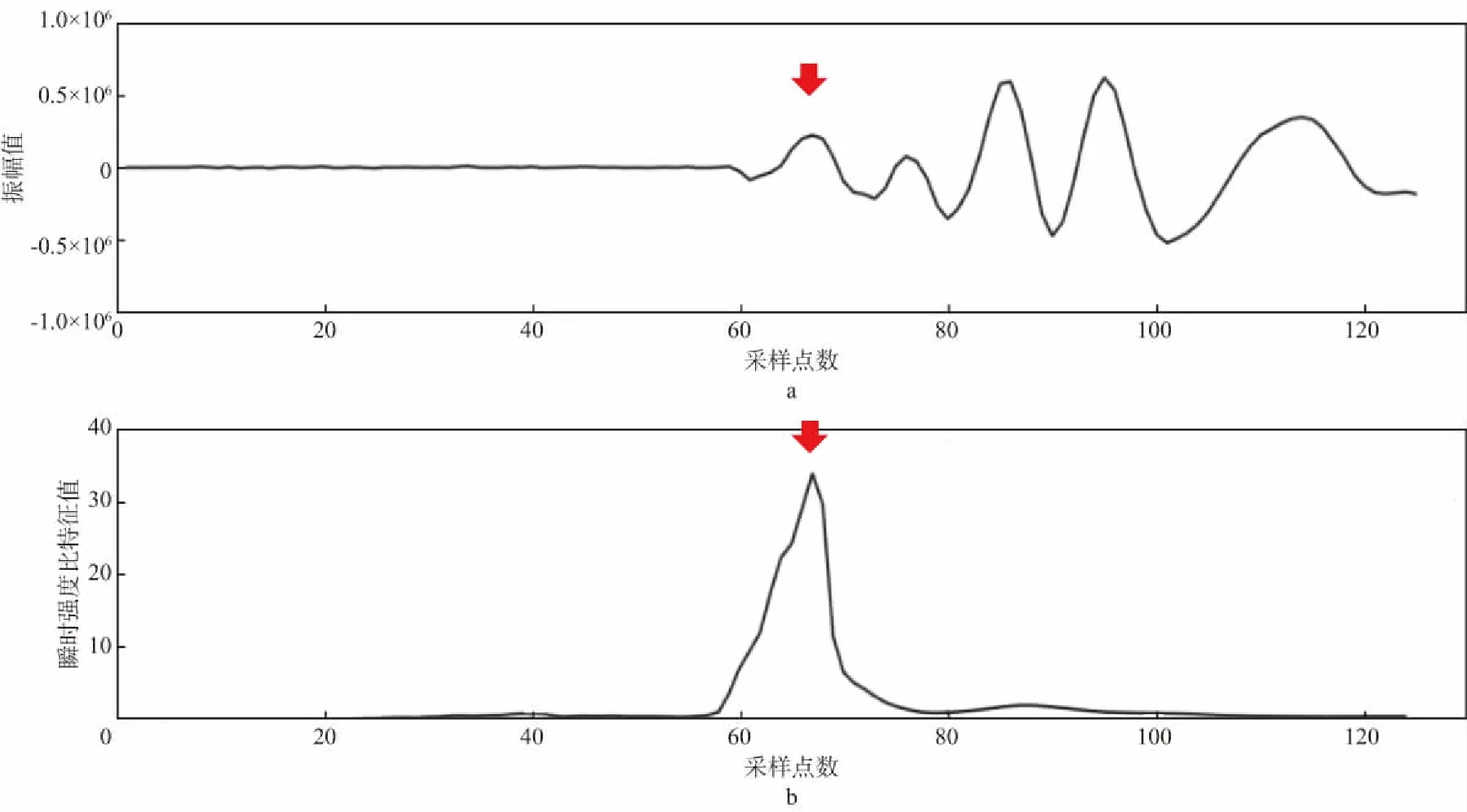
图7 地震道及各样点强度比a 地震道; b 各采样点处强度比
然而,并不是所有的强度比最大值都能用于确定初至的位置,特别在初至波到达前有较强的随机干扰时。尽管可以用曲波变换方法压制随机噪声,但是在去噪时应该遵循“温和”去噪的原则,否则可能使初至波的能量特征和波形特征发生较大改变,影响初至拾取的准确度。因此,在利用曲波变换对单炮进行“温和”去噪的基础上,同时需考虑提高初至拾取方法自身的抗噪能力。改进的强度比计算公式如下:
(10)
式中:R为前后时窗中样点总数。
图8展示了去噪前后某单炮道号为101的地震道(黑色实线)和瞬时振幅(绿色虚线)。对比可以发现,去噪之前,初至信号湮没于能量强的随机噪声之中,难以辨识;去噪后,尽管初至波前仍然有随机噪声且能量不弱,但是初至波信号已可以辨识,其相对振幅值及瞬时振幅较大,说明采用的去噪策略取得了一定的效果,去噪后的数据有利于初至拾取。
图9a为图8a中的地震道;图9b为该道各样点处的传统型强度比,显然,根据该强度比无法拾取到准确的初至时间(绿色箭头);图9c为该道各采样点处的改进型强度比,根据该强度比则可以确定初至波的位置(红色十字星),即采样点序列号为63,初至时间为252ms。
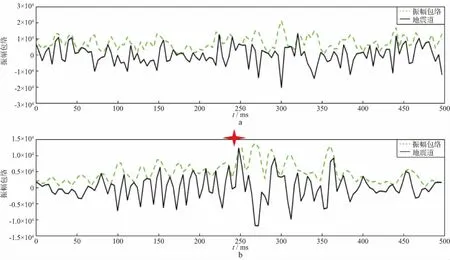
图8 地震道及瞬时振幅a 去噪前; b 去噪后
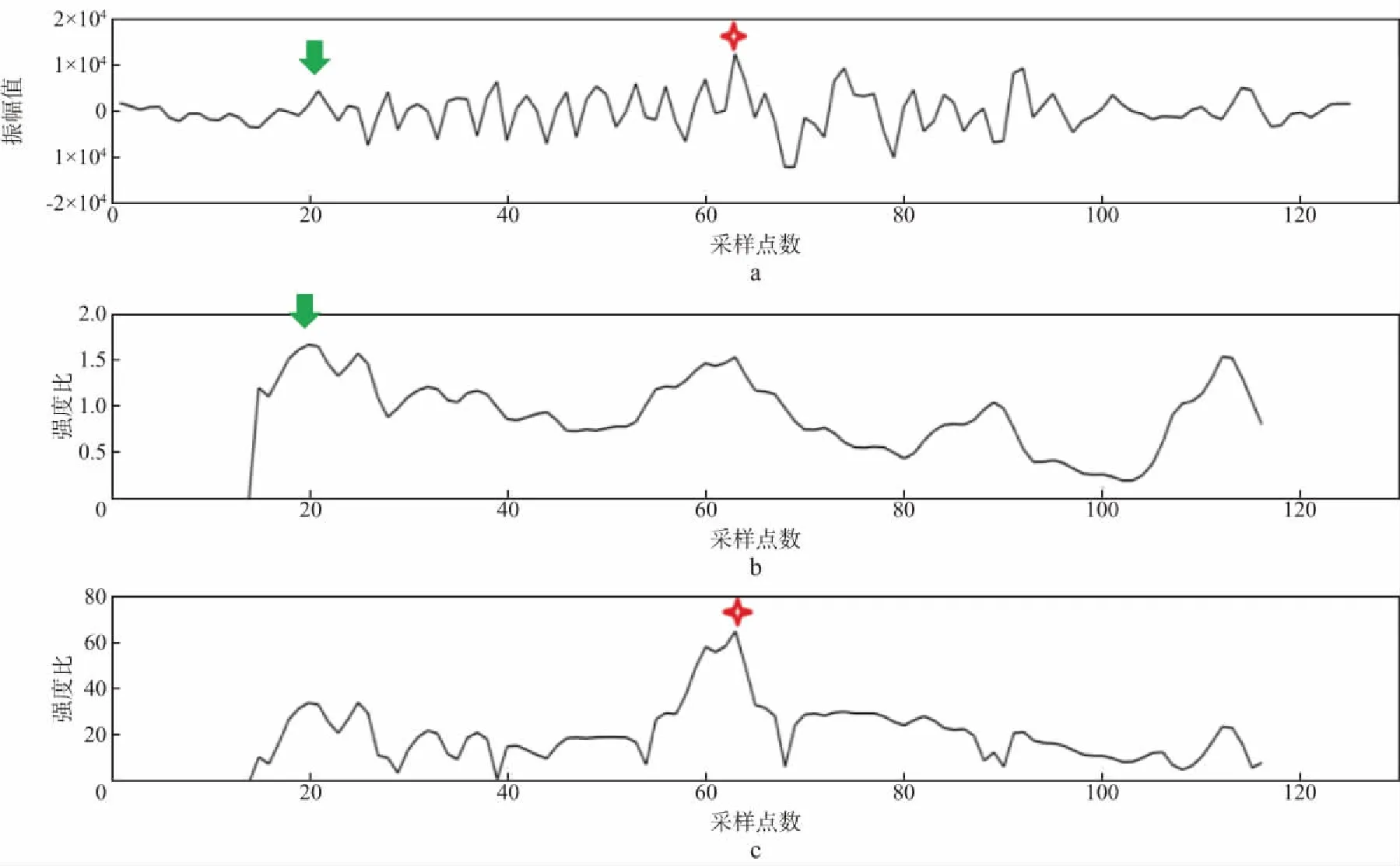
图9 地震道及不同方法强度比a 地震道; b 传统型强度比方法; c 改进型强度比方法
表1给出了分别采用传统型和改进型方法拾取的部分道初至时间与手工拾取初至时间的误差,数据采样间隔为4ms,采用的前滑动时窗为60ms,后滑动时窗为30ms。由表1可以看出,传统型误差最大达到148ms,而改进型最大仅为4ms,因此与采用传统型方法相比,改进型方法拾取的初至时间更准确。
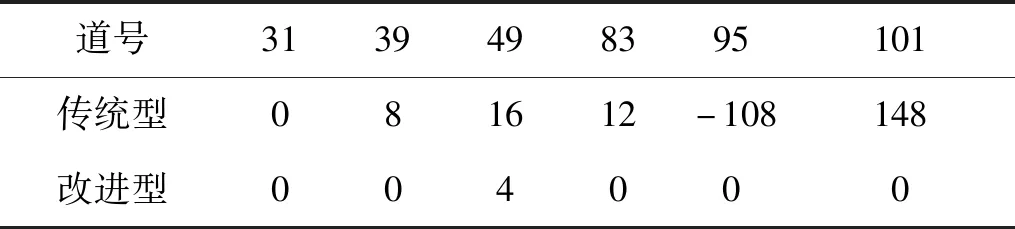
表1 不同方法拾取初至时间误差 ms
1.3.2 异常初至处理
利用改进型强度比法自动拾取初至,有可能存在与利用滑动时窗能量法拾取初至一样的问题[28],即
最大的强度比不一定对应初至波的能量,也就是初至时间并不一定对应于强度比的最大值或第一极值,也有可能是第二极值,甚至第三极值等。那么该如何自动判断拾取第一极值还是其它极值呢?
基于地表一致性假设,应用静校正和线性动校正的地震资料,同一炮相邻两道之间的初至时间应该不存在较大差异。如果存在,则应是拾取的初至时间不正确。
在共炮点道集内,各道拾取的初至时间记为ti,i为道号(i=1,2,3,…,N),N为最大道数[28]。
记相邻两道的初至时间差为:
ΔTi=|ti+1-ti|
(11)
初至时间差的均值记为μ,其标准方差为σ。定义:
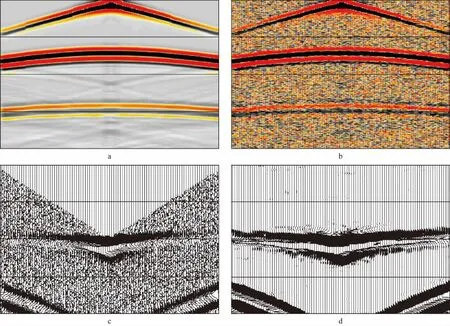
|ΔTi-μ| (12) 如果满足(12)式,则被认为是正确的初至时间,否则,被认为是错误的初至时间。k为误差控制系数,可以根据初至质量进行试验。 在检测到错误的初至时间后,将初至时间更新为强度比第二极值所对应的时间。再重新根据(11)式计算相邻两道的初至时间差、均值和方差,并用(12)式进行检测,是否满足该式。如果不满足,则继续用强度比第三极值对应的时间更新初至时间并检测。重复上述检测过程,直到找到正确的初至时间,使其满足(12)式的要求。 在完成前述的工作之后,拾取的初至时间可能并不是精确的波峰时间,有可能是波谷或过零点时间,也有可能是初至波一个周期内的任意一点。为能够拾取到精确的波峰时间,应用相位域波峰追踪技术[29]精确确定初至波波峰的位置。 本文提出的低信噪比资料初至自动拾取方法技术的实现可总结如下: 1) 输入应用检波点高程静校正及线性动校正的炮集数据; 2) 对步骤1)中输出数据进行曲波变换,在曲波域内选择合适阈值压制随机噪声,然后通过反变换得到去噪后的数据,提高初至波的信噪比; 3) 对去噪数据做希尔伯特变换并构建地震复数道,然后利用公式(7)计算各道的瞬时振幅; 4) 利用公式(10)计算每一道各采样点处的强度比,而后根据强度比极值判断初至波的位置; 5) 应用异常初至检测与修正技术改善自动拾取结果; 6) 应用相位域波峰估算法精确确定初至波波峰的位置; 7) 输出经过反高程静校正及反线性动校正的初至时间。 为验证本文方法的有效性,建立了2层速度模型,速度分别为1500m/s和3200m/s,深度为400m,记录长度为0.8s,采样间隔为1ms,地震子波为雷克子波,主频30Hz,道距5m,总道数101道。利用射线法进行正演模拟,得到如图10a所示的单炮记录,记录中包含了直达波,反射波及多次波;图10b为加入高斯噪声后的单炮记录,信噪比为0.35,随着偏移距由近及远,信噪比逐渐降低,远偏移距初至波的信噪比非常低;图10c是经动校正后的记录(线性动校正时窗中心点位置为200ms),道号1~11及90~101范围内初至波能量较弱,信噪比低,较难辨识初至信号;图10d是去噪后的动校正记录,初至波的信噪比明显提高,能够清晰地辨识初至信号,即提高了自动拾取初至的准确度。 图10 理论数据测试a 模拟单炮记录; b 加入高斯噪声记录; c 线性动校正记录; d 去噪后记录 图11中,用黑线表示对模型数据进行人工拾取的初至,而利用本文方法自动拾取的模型数据、加噪数据、去噪数据的初至分别用红线、蓝线和绿线表示。可以看出,红线、绿线及黑线基本重合在一起,说明了在模型数据及去噪数据上应用本文方法可以拾取到较准确的初至时间。蓝线与其它线有不同程度的偏差,特别是远炮检距处,偏差较大,最大达192ms,说明尽管根据瞬时强度比提出的自动拾取方法有一定的抗噪能力,但是当信噪比很低时,仅利用强度比法仍然难以拾取到准确的初至。因此,当资料信噪较低时,利用本文方法(即首先利用曲波变换法去噪,然后应用强度比法自动拾取初至)能够提高初至拾取的准确率。 图11 初至拾取结果 为测试本方法处理实际资料的能力,将该方法应用于某工区地震资料的初至拾取中。道距20m,炮距40m,采样间隔1ms,记录长度为5s,一炮两线,滚进滚出施工。该区域资料近道信噪比相对较高,而中远道因存在能量相对较强的随机噪声而导致信噪比相对较低。采用现有软件自动拾取,通常在近道能够取得较好的拾取效果,而在部分中远道效果较差,导致后续依赖于初至时间计算的静校正量存在问题。 图12分别是应用不同方法拾取结果的CMP道集显示,CMP号为465,偏移距范围3690~5953m。图12a是应用软件拾取结果;图12b为应用本文方法拾取结果;图12c为人工拾取结果。与人工拾取相比,采用软件自动拾取有19道未拾取到准确的初至时间,初至前的随机噪声对初至拾取影响较大。采用本文方法拾取,除偏移距4650m处因子波“分叉”,偏移距5409m和5932m处两道因能量极弱之外,其余各道中均拾取到准确的初至时间。表明在低信噪比资料中,应用本文方法能够较大幅度提高自动拾取初至的精度。另外,尽管采用本文方法拾取的初至与人工拾取的初至时间存在偏差,但是与采用软件拾取相比,这种偏差实际上较小,采用软件拾取最大偏差达几百毫秒,而本文方法最大偏差为23ms。 图12 初至拾取结果CMP道集显示a 某软件拾取; b 本文方法拾取; c 人工拾取 实际资料应用结果表明,当初至波能量较弱,信噪比很低时,利用本文方法可以提高自动拾取初至的精度,减少处理人员的工作量。 针对低信噪比资料初至自动拾取困难的问题,提出了一种先利用曲波变换去噪提高资料信噪比,再利用具有一定抗噪能力的强度比法实现对低信噪比资料初至自动拾取的方法,取得了较好的应用效果。并得到以下结论及建议。 1) 首先计算每道各采样点处的瞬时强度比,根据强度比极大值确定初至波能量,然后通过异常初至检测及修正技术改善初至拾取结果,再利用相位域波峰追踪技术精确确定初至时间,最后可以得到精度较高的单炮初至。 2) 针对低信噪比资料,将“温和”去噪与具备一定抗噪能力的改进型自动拾取方法相结合,共同解决初至自动拾取的难题,最大程度减少人工修改错误初至的工作量。 3) 应用本文方法拾取初至,需要在去噪过程中保护好初至信号。但是就如何做好保护工作,需要进一步就信噪比、信号保护程度、初至准确度及拾取方法抗噪能力之间的关系开展深入研究。 4) 实际资料总是复杂多变的,影响初至拾取也不仅限于随机噪声干扰,描述初至波特征也不仅限于瞬时强度。有必要进一步研究初至波特征以及影响初至波的各种因素,研究利用多种属性进行初至波描述的方法。2 应用实例
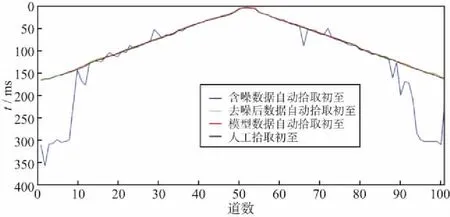
2.1 理论数据测试
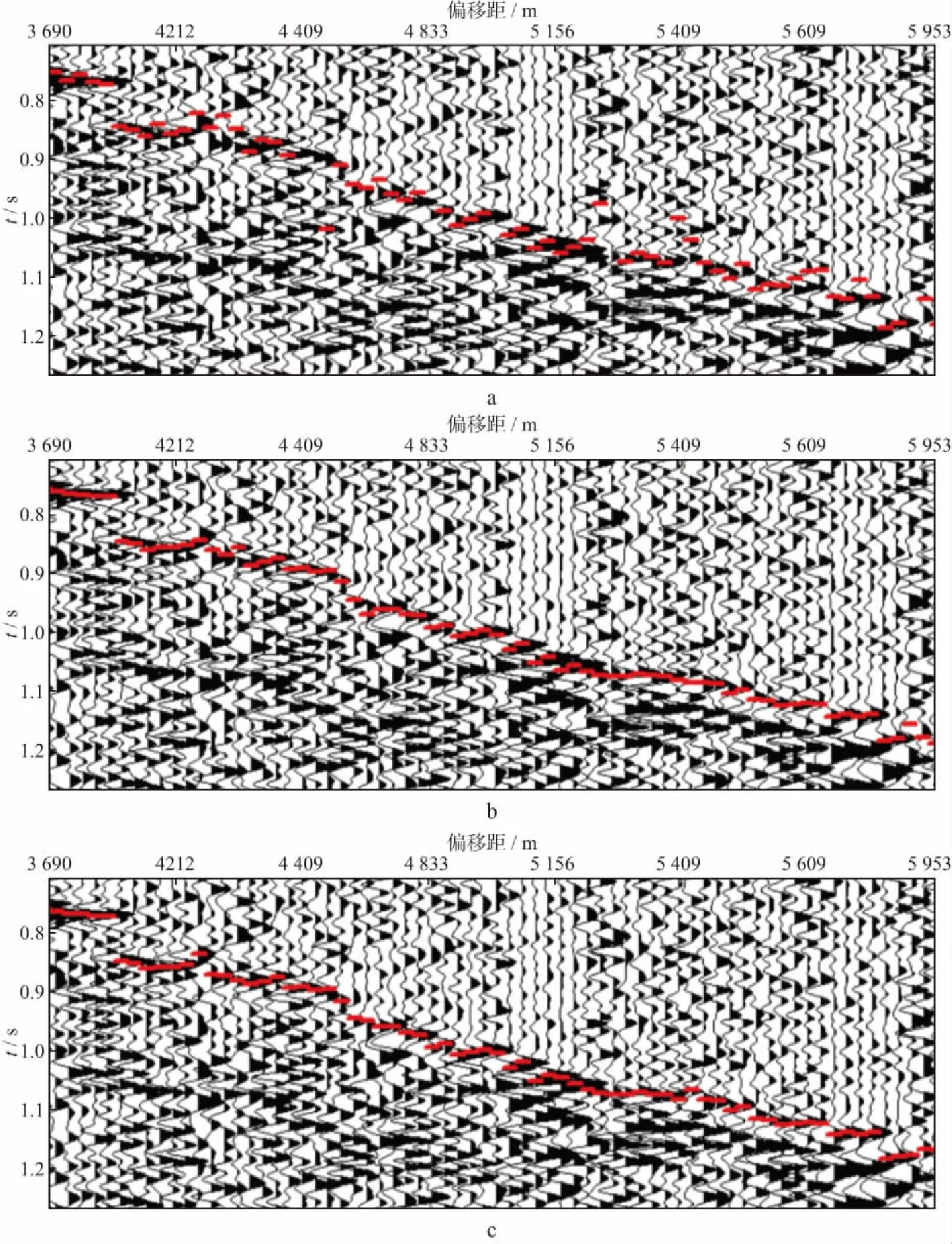
2.2 实际数据
3 结论
