一种基于BP神经网络的铁路大宗货物运价风险预警判定方法

曾 进，郭少媛，戚芳榕，潘红芹，董宝田

（1.北京交通大学 综交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2.中国铁路信息科技集团有限公司 信息工程管理部，北京 100844）

随着运输市场的竞争愈加激烈，铁路货物运输的发展受到多方制约，为了获取更大的市场份额和利润，需要对货物运价做出实时的风险预警。已有众多学者对该领域进行了研究。魏方[1]研究干散货远洋运价市场波动风险评估，提出长记忆性波动风险评估、极端性波动风险评估、相关性波动风险评估系统方法。钱芳[2]阐述了中国航运市场运价预警机制的框架，并在研究支持向量机模型的基础上，建立中国航运市场运价预警模型架构。朱玉华[3]运用ARIMA 模型分析了我国出口集装箱运价指数的变动趋势，并依据金融风险预警理论,建立了我国出口集装箱运价风险预警机制模型。孙祖妮[4]分析我国铁路运输成本的构成及影响因素，以某铁路运输企业货运成本预测为例，分别用成本动因神经网络预测方法和灰色系统预测方法进行预测。张锁[5]通过以定量分析为主、结合定性分析的方法,建立了基于VaR-GARCH 的风险度量模型,对市场风险进行研究。曹雪玲[6]等人通过分析铁路危险货物运输风险因素，构建铁路危险货物运输风险评价指标体系并应用模糊综合评价法对铁路危险货物运输风险进行评价。张光宇等人[7]进行了铁路货运价格管理系统的设计与开发，为做出合理的运价风险预警提供了参考。

以上风险预警方法均采用各指标的历史数据，因其不能准确反映未来情况，使预警效果较易产生大的偏差。Bowersox 和Donald.J[8]带领的研究小组于1999 年应用神经网络算法进行物流成本研究，对宏观物流成本进行估算。2003 年，Bowersox 小组再次采用人工神经网络，以2000 年的数据为标准估算国家物流成本[9]。2005 年，Alexandre M.等人[10]建立了6 层人工神经网络模型。使用神经网络算法既考虑了历史数据，又利用到实时数据，使得输出的数据与期望值更为近似。BP 神经网络是应用最广泛的神经网络之一，但目前还较少有使用BP 神经网络算法对铁路运价进行风险预警的实例。

1 基于BP神经网络算法的铁路运价风险预警模型

1.1 模型构建

本文选用典型的3 层BP 神经网络结构模型，对大宗货物铁路运输价格的风险进行预警。图1 为该模型的拓扑结构。

图1 BP神经网络拓扑结构

图中，xi(i=1,2,…,n)表示输入数据；yj(j=1,2,…,m)表示输出数据。

（1）确定输入节点数

基于BP 神经网络算法的铁路运价风险预警模型的输入应该为能全面描述铁路运价风险的影响指标，这些指标来自于宏观经济、运输市场、货主与铁路企业4 个方面。

（2）确定输出节点数

输出节点的个数对应需要进行风险预警的指标个数。在铁路价格预警中，输出节点个数为1。

（3）确定隐含层节点数

王选院士钻研创新的科研精神深深影响着他的学子，本次寻访的主角肖建国便是其得意的门生之一。在王选院士的指导和自身的不懈努力下，肖建国在计算机技术、图像影像处理、网络信息处理和排版印刷领域都取得了重大成就，推动了中国印刷技术的发展。同时圣为人师，培育英才，让研究精神和技术与时俱进，代代相传。

关于隐含层节点数的确定问题，实践中常用经验公式来取值，计算公式为：

其中，p为隐含层节点个数；m为输出层节点个数；n为输入层节点个数；a取1 ～10 之间任意一个常数，当根号内计算结果非整数时，采用四舍五入原则进行运算。

1.2 铁路运价风险预警指标体系的建立

风险预警的主要目的是根据预警指标的变化情况，反映风险的等级，要实现铁路运价风险的合理预警，选择合理的指标十分关键。本文根据铁路货运运营的具体情况以及指标选取原则，从宏观经济、运输市场、货主和铁路企业4 个方面选取了21 个预警指标，建立的风险预警指标体系如图2 所示。

图2 铁路运价风险预警指标体系

图中将21 个指标进行分类标号，与宏观经济相关的4 个指标为A 类，与运输市场相关的11 个指标为B 类，与货主相关的4 个指标为C 类，与铁路企业相关的4 个指标为D 类，再逐一对每一类编号。

1.3 样本数据归一化

为了消除数据量纲的影响，BP 神经网络的信息由输入层向隐含层传送时，需要使用转换函数。为方便对输入信号进行学习，将输入信号进行收敛，本文选取S 型函数的正切形式tansig 函数作为隐含层节点和输入层节点的激活函数；线性函数Purelin 的输入值和输出值可以取任意值，故此处选取线性函数Purelin 作为输出层节点的转换函数。

为满足BP 神经网络转换函数对数据输入的要求，本文采用Matlab 软件对原始数据进行归一化处理，采用的归一化方法为（0，1）标准化法，计算公式为：

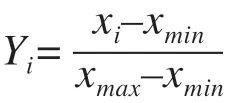
其中，Yi为数据i的归一化结果；xi为数据i的实际值；xmin、xmax分别为该组数据的最小、最大值。

1.4 神经网络训练

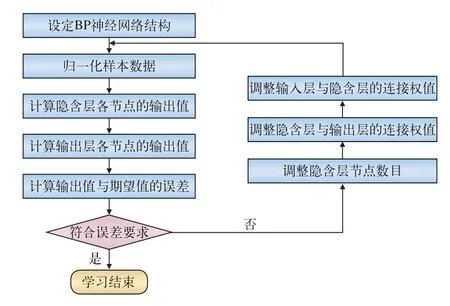
图3 BP神经网络学习流程

2 案例分析

2.1 样本数据的采集

铁路大宗货物运输占全部品类运输的70%以上，而其中煤炭类运输又占到大宗货物品类运输的60%以上，本文选取煤炭的铁路运输做为案例的主要分析对象。在铁路运输的竞争者中，公路运输最为主要，在800 km 以上的中长运输距离中，铁路的竞争优势便开始体现，应该保证铁路运输在这部分市场占有较大的市场份额，故取800 km ～1500 km 中长距离运输范围进行模型验证。

本文选取2015—2017 年影响铁路运价的月度指标数据，每月数据为1 组，共36 组，作为原始样本数据。随机选取其中的27 组作为训练数据，剩余9组作为验证数据。本文对互联网上可获取的资料进行挖掘与整合，采用了来源于国家统计局、国家发改委、中国统计年鉴、中国铁道年鉴及鄂尔多斯煤炭网等的相关数据，涉及宏观经济数据、铁路货运情况数据、公路运价指数及各种车型的公路平均运价等指标。

2.2 预警级别的确定与划分

在预测出未来的铁路运价预警指数之后，判断运价的变动是否存在风险，若存在风险需要进一步划分预警级别，使管理人员可根据预警级别制定相应措施。

对所选取的各组指标数据划分预警级别，需先确定各组风险预警的综合预警指数。综合考虑煤炭各月的公铁运价比值和运量比值双项指标，来确定当月的经营效果。由于公路煤炭运量数据无法获取，因此将运量比这一指标改为铁路煤炭运量进行分析，而由于二者数量级相差较大，故在之后的分析中应先消除数量级的差异。当煤炭在该月的公铁运价比值较低且运量数据也较低时，则需要进行风险预警。根据上述分析，将以上2 指标消除数量级差异后的比值作为综合预警指数，划分风险预警范围，得出各组数据的预警级别如表1 所示。

本文预警级别的划分标准为：

（1）若综合预警指数在[0，0.71）范围内，则铁路运输价格预警级别为正常（绿色）；

（2）若综合预警指数在[0.71，0.90）范围内，则铁路运输价格预警级别为蓝色风险预警；

（3）若综合预警指数在[0.90，1.00）范围内，则铁路运输价格预警级别为黄色风险预警；

（4）若综合预警指数在[1.00，1.10）范围内，则铁路运输价格预警级别为橙色风险预警；

（5）若综合预警指数≥1.10，则铁路运输价格预警级别为红色风险预警。

2.3 模型运行情况与结果分析

2.3.1 隐含层节点个数的确定

本文建立的BP 神经网络模型的输入层节点个数为21，输出层节点个数 为1。 由经验公式可以确定隐含层节点个数应该在6 ～15 之间，需要经过多次训练确定隐含层节点具体个数，并在训练过程中计算不同网络节点数的训练误差。隐含层的激活函数采用tansig 函数。

对网络进行训练，当网络满足设定的期望误差或达到最大训练步数时，训练结束，可得到不同隐含层神经元个数对应的训练所得误差，如表2 所示。通过比较可以发现隐含层节点个数为13时，网络的训练误差最小，所以选定隐含层节点的个数为13 个。

表1 铁路运价预警级别划分

表2 不同节点个数对应的误差值

2.3.2 模型训练与结果分析

随机选取27 组样本数据对基于BP 神经网络的铁路运价预警模型进行训练，设学习速率为0.05，由图4可知,在1 427次迭代后，训练误差逐渐趋于0。

由表3 可知，模型训练的结果与实际值十分接近。

图4 铁路运价预警模型误差训练曲线

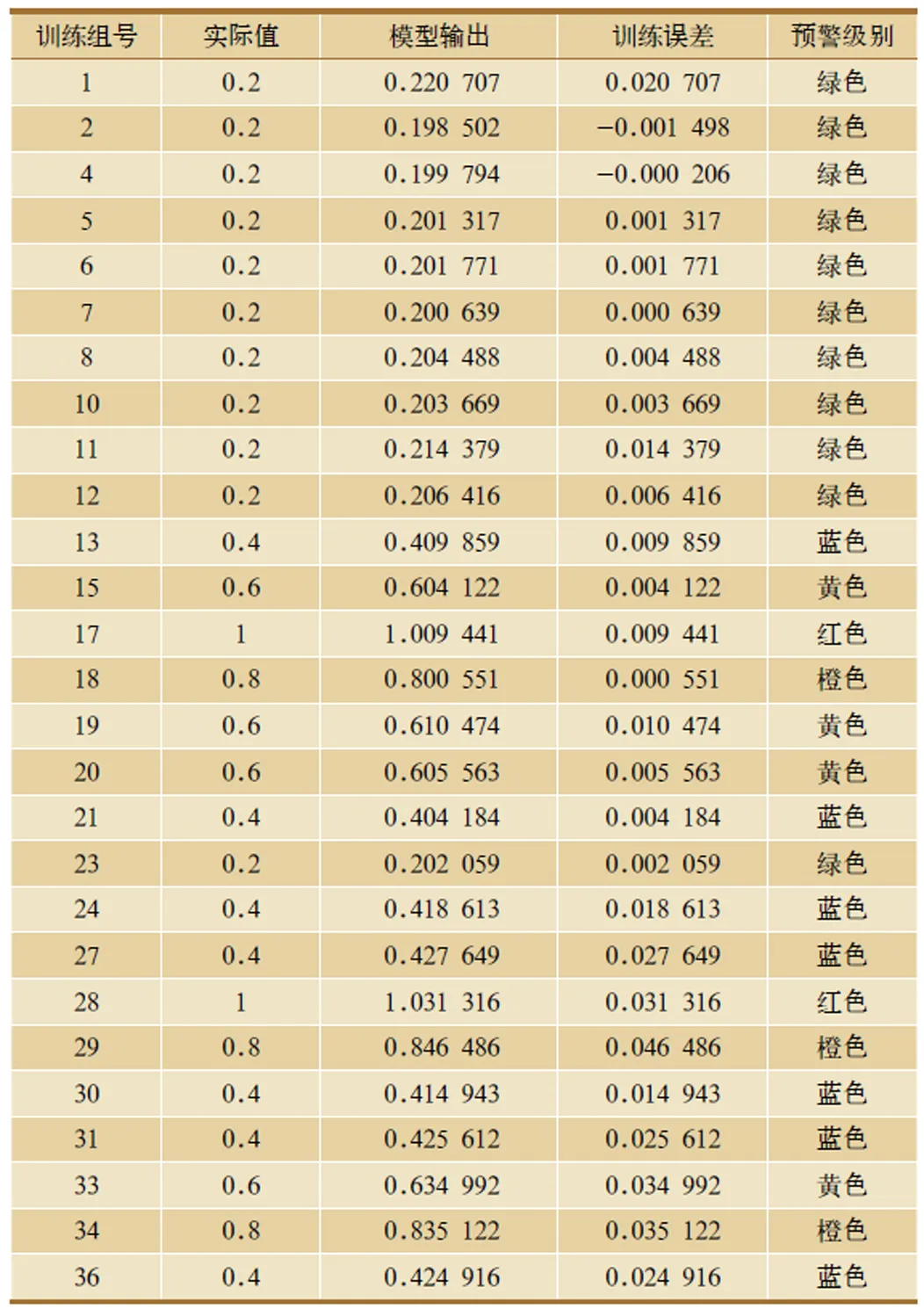
表3 铁路运价风险预警模型训练结果

以其余9 组样本的数据为输入数据，输入以上建立的铁路运价风险预警模型进行验证，结果如表4 所示。

从表4 可以看出，随机选取的9 组数据的模型输出值与实际值十分接近，误差较小，风险发生预警级别与实际相同。因此可以证明本文建立的神经网络模型符合要求，可以用于铁路运价的风险预警。

表4 铁路运价风险预警模型检验结果

3 结束语

本文通过建立铁路运价风险预警模型，验证了基于BP 神经网络算法进行铁路运价风险预警的可行性，并且为其他领域风险预警模型的建立提供了参考。通过建立铁路运价风险预警模型，可以有效地对铁路运价进行合理调控，为铁路运输部门在货运管理和货运成本控制等领域提供准确及时的信息，丰富铁路运输企业的运价管理手段。