基于响应曲面法的高速内冷铣削AISI304不锈钢铣削力
2020-07-24李广慧尹凝霞谭光宇
薛 姣 李广慧 尹凝霞 沈 灿 谭光宇
(广东海洋大学机械与动力工程学院,湛江 524088)
文 摘 针对硬质合金刀具高速内冷铣削AISI304不锈钢时,切削力大、切削温度高及加工表面质量低的问题。基于响应曲面中心复合设计方法进行高速内冷铣削实验,建立了铣削力分量二阶回归预测模型,并进行了实验验证。对比了干式与内冷铣削后的加工表面质量,分析了铣削参数对铣削力分量的影响规律,以铣削力分量最小为目标优化了铣削参数。结果表明:进给力和径向力的预测值与实验值的误差分别为4.77%和6.16%;内冷铣削的Ra 为0.193~0.327µm;对铣削力分量的影响是铣削深度>转速>进给量,随着铣削深度和转速的增加,进给力先升高后降低,径向力逐步增加,铣削深度与转速的交互作用对进给力和径向力的影响显著;转速11 643.63 r/min、铣削深度1 mm、进给量0.08 mm/r为最优铣削参数组合。
0 引言
AISI304 不锈钢因在高温腐蚀的环境下依然具有优良的综合性能而广泛应用于航空、船舶、医疗等高技术领域,是一种常用的宇航材料,如飞机发动机冷端叶片[1]。但其热导率低、塑性强使它在切削加工过程中具有切削力大、表面质量难以控制以及加工硬化严重的特点,导致刀具磨损加剧、粘屑、耐用度降低[2-3]。
高速铣削是一个复杂的非线性铣削加工过程,加工表面的质量和切削力都与切削过程中的冷却方式紧密相关。张春燕等[4]对钛合金进行了内冷式MQL 铣削实验,分析了铣削参数对已加工表面质量的影响。邵军杰等[5]对1Cr18Ni9Ti 奥氏体不锈钢进行了平面铣削实验,建立了表面粗糙度和铣削力模型。孙燕华等[6]通过正交实验和多元线性回归建立了0Cr18Ni9铣削力模型。但是对0Cr18Ni9铣削力及刀具的研究主要是干式或外冷的铣削环境,内冷式微量润滑设备昂贵且操作复杂。内冷铣削是指切削液经过刀具内部螺旋孔,从刀具低刃端直接喷到切削区域对刀具及切削区域进行冷却润滑。切削液能够有效达到切削区,并在刀具与切屑间形成润滑膜,大大降低了刀屑之间的摩擦,减少了刀具磨损,提高了表面加工质量。因而研究高速内冷铣削过程中铣削力的变化规律,影响铣削力的主要铣削因素,建立可靠的铣削力模型对减少刀具的磨损、保证加工完整性等具有重要意义[7-9]。
本文重点对高速内冷铣削力进行研究,通过响应曲面中心复合实验与单因素实验,建立铣削力分量预测模型,分析铣削参数对铣削力的影响规律,以铣削力分量最小为目标得出最优铣削参数组合,拟为工程实践提供参考。
1 高速铣削实验
1.1 设备
采用VMC1000P 主轴出水立式加工中心(主轴最高转速15 000 r/min,机床额定功率11 kW),Kistler9119AA1 切削力测量系统(测量范围0~4 kN,灵敏度进给力Fx≈-26 Pc/N,径向力Fy≈-13 Pc/N),采样频率13~26 kHz;Mar Surf PS1 粗糙度测量仪,BT40 刀柄,动平衡等级G2.5/2000 RPM,实验测力原理示意图如图1所示。

图1 测力原理示意图Fig.1 Schematic diagram of force measurement
1.2 实验条件与方案
采用GU20整体硬质合金4刃双螺旋内冷孔立铣刀,直径10 mm,前角5°,后角15°,螺旋角30°,内冷孔直径1.4 mm,内冷压力0.3 MPa(表压)。测试材料是AISI304不锈钢[10],尺寸为64 mm×40 mm×80 mm,DX-2型切削液,采用高速内冷铣削,铣削方式为平面顺铣。中心复合设计(CCD)方法具有能评估高阶多项式预测模型、实验循环次数少、建模便捷以及预测结果贴近真实值等优势而在工程中广泛应用[11]。
根据机械加工工艺手册、工件及铣刀材料选择实验铣削参数,实验设计如表1所示。

表1 实验因素与水平Tab.1 Experimental factors and levels
2 结果分析与讨论
2.1 实验结果
通过铣削实验获得三个方向铣削力,其中轴向力Fz在铣削过程中波动较小且关于零轴对称分布,故本文只分析Fx和Fy,铣削力取切削稳定区连续30个峰值的平均值,1~20 组为中心复合实验,21~26 组为补充实验,实验结果如表2所示。

表2 实验结果Tab.2 The experimental results
2.2 内冷铣削力模型的建立与方差分析
响应曲面法能够反映响应值与响应因子之间的关系,克服了正交实验不能给出直观图的缺陷。假设影响因素显著性水平P<0.05,采用响应曲面中心复合法对铣削力分量与铣削参数之间的关系进行分析,根据实验数据运用最小二乘法拟合二阶回归方程模型,并对其进行方差分析以判别模型拟合的优良程度,二阶数学模型如下[12]:

式中,y为响应值,x为铣削因子变量,βo、βi、βii、βij分别为各项系数。
通过形式转换,把实验因素的自由变量和铣削力分量值转换成矩阵形式,再运用最小二乘法得到上式中的系数值,最后经过铣削参数转换,建立铣削力分量与铣削因子间的多元回归预测模型,即:
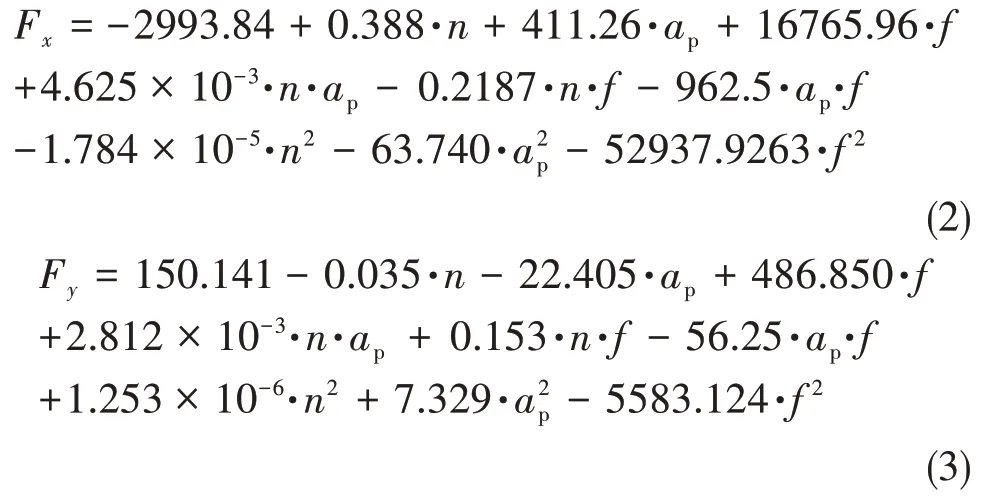
建立二阶回归模型后,进行方差分析,结果见表3[13]。

表3 回归模型方差分析表Tab.3 ANOVA table for the regression model
由表3可知,Fx方差分析模型中P<0.000 1,模型非常显著,多元相关系数R2=0.997 1,校正后的多元相关系数Radj2=0.994 6,表明二阶模型拟合结果较好。Fy方差分析模型中P<0.000 1,模型非常显著,多元相关系数R2=0.947 6,校正后的多元相关系数Radj2=0.940 4,对实验结果的拟合程度高。
2.3 铣削力分量模型的验证及单因素对铣削力分量的影响分析
通过三组单因素实验进行验证模型的准确性,并分析了单因素对铣削力分量的影响,具体结果如图2所示。从图2中看出,不管是Fx还是Fy,内冷实验值与预测值在不同转速、不同铣削深度、不同进给量下变化趋势均一致,Fx的内冷实验值与预测值的误差是4.77%,Fy的内冷实验值与预测值的误差是6.16%,表明铣削力分量预测模型的可靠性高。
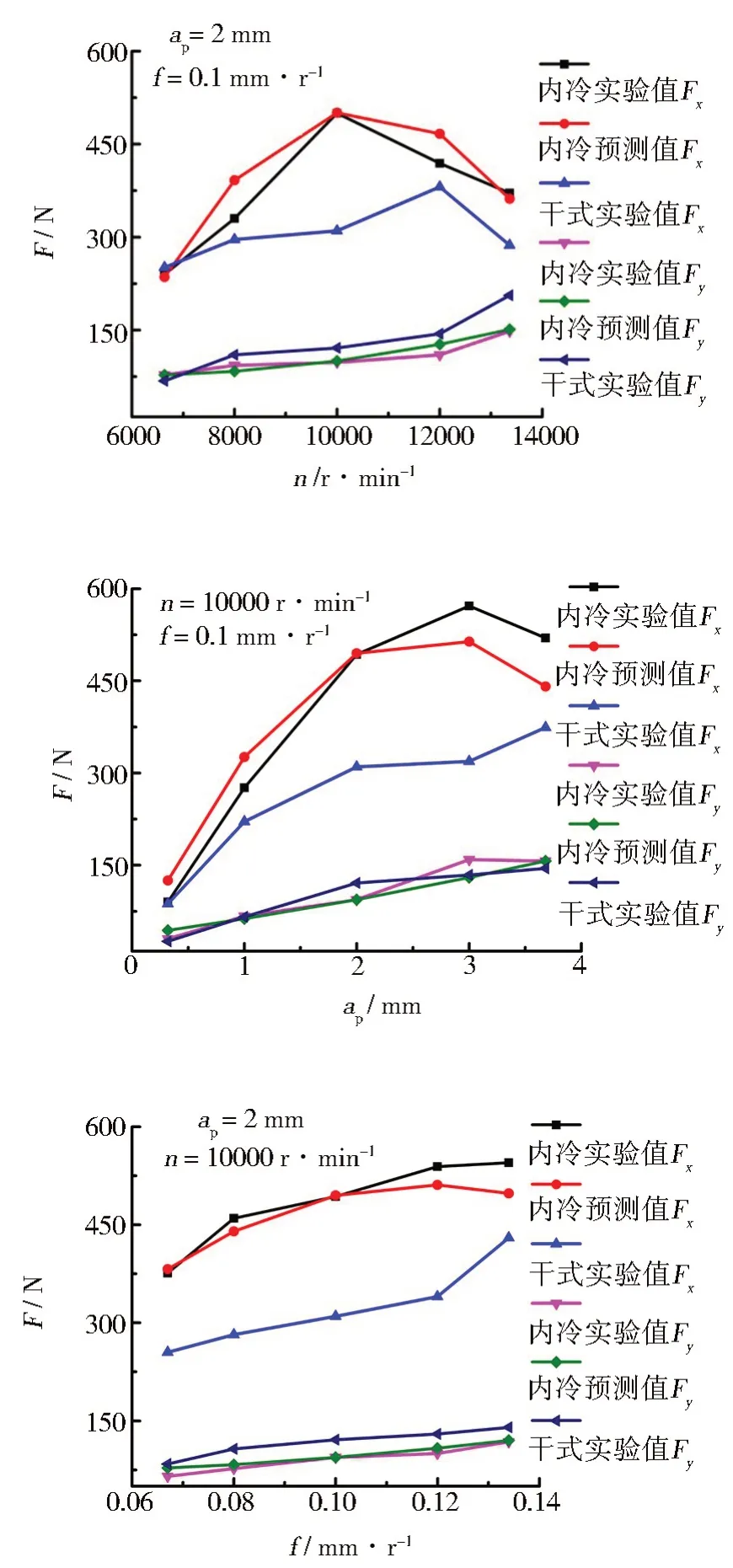
图2 单因素对铣削力分量的影响Fig.2 Effect of single factor on milling component force
Fx内冷实验值高于干式实验值,是因为在切削液的作用下,切削温度下降,减小了加工表面的热软化,使得铣削力增大[14];其次,切削液经内冷孔喷出,在离心力的作用下冲击待加工表面,增大了铣削力。Fy的内冷实验值略低于干式实验值,不同的铣削环境对Fy的影响不明显。对加工后的表面进行测量,内冷铣削后的工件Ra为0.193~0.327µm,干式铣削后的工件Ra为0.330~0.488µm,内冷铣削的表面质量优势显著。在图2中,当转速在6 636~10 000 r/min时,Fx增加,在10 000~13 364 r/min时,Fx减小,最大值为500 N。这是高速切削的特征之一[15-16],当工件材料被切削的速度超过了其本身滑移变形的速度时,材料还没有来得及完成滑移变形就被切掉了;第二切削速度的增加使得被切材料脆性化,铣削力减小。铣削深度在1~3 mm时,Fx增加,在3~4 mm时,Fx减小,最大值为572 N;随着进给量的增加,Fx缓慢增加。
Fy随着转速和进给量的增加增速较小,随着铣削深度的增加,先增加后平缓减小。
2.4 交互因素对铣削力分量的影响
根据二阶回归方程模型做出铣削参数间交互作用的三维立体响应曲面,结果如图3和图4所示。
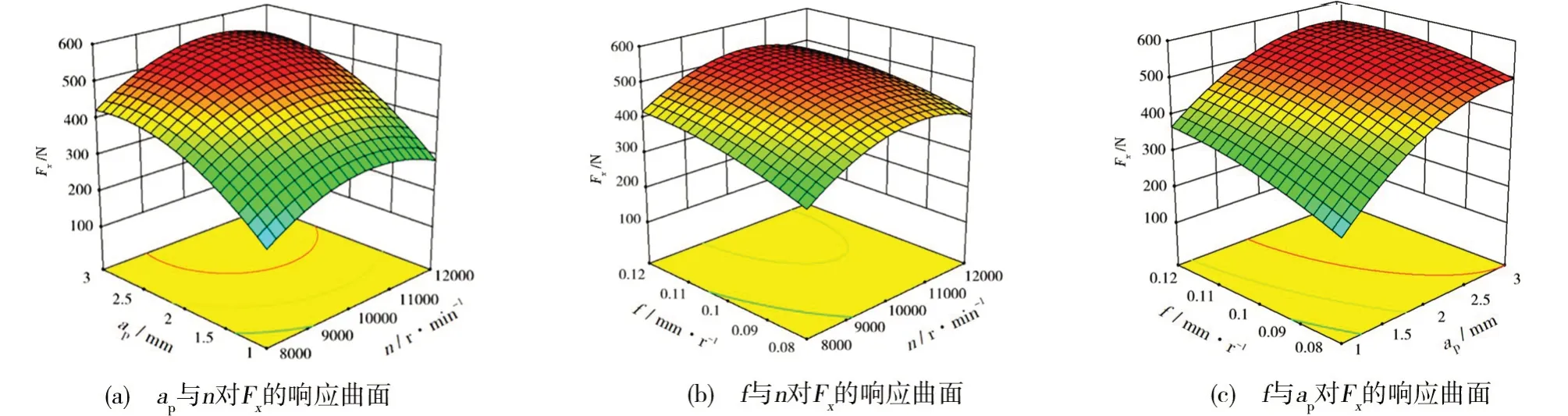
图3 Fx的响应曲面图Fig.3 Response surface diagram of Fx

图4 Fy的响应曲面图Fig.4 Response surface diagram of Fy
在图3(a)中的曲面弯曲幅度和目标值范围明显大于图3(b)和图3(c),可知铣削深度与转速之间的交互作用对Fx的影响大于铣削深度与进给量的交互用及进给量与转速的交互作用。从图3(a)和图3(b)中得知在铣削深度和进给量不变的情况下,Fx随着转速的增加先增大后减小,其原因与上述高速机理相似。由图3(a)和图3(c)中得知在转速和进给量不变的情况下,Fx随着铣削深度的增大先增加后缓慢减小;由图3(b)和图3(c)中得知在铣削深度和转速不变的情况下,Fx随着进给量的增加缓慢增加至趋于稳定。
从图4(a)和图4(b)中得知在铣削深度和进给量不变的情况下,Fy随着转速的增加稳步增大;由图4(a)和图4(c)中得知在转速和进给量不变的情况下,Fy随着铣削深度的增大而线性增长;由图4(b)和图4(c)中得知在铣削深度和转速不变的情况下,Fy随着进给量的增加缓慢增加至趋于稳定。
2.5 铣削参数优化
根据上述高速内冷铣削单因素实验及铣削参数的交互作用对铣削力分量的影响变化分析可知,对铣削力分量的影响是铣削深度>转速>进给量,因此应选择低的铣削深度、高转速和小进给量来获得最小铣削力分量。以此为基础,在所选的铣削参数范围内,结合二阶响应模型采用最小二乘法求解,得到转速11 643.63 r/min、铣削深度1 mm、进给量0.08 mm/r,此为铣削力分量最小的铣削参数组合。
3 结论
(1)建立高速内冷铣削的铣削力分量预测模型,并通过方差分析和实验验证了预测模型的可靠性高。Fx和Fy的预测值与实验值的误差分别为4.77%和6.16%。
(2)对铣削力分量的影响是铣削深度>转速>进给量。Fx随着铣削深度和转速的增加先增加后减小,转速在10 000 r/min 时达到最大值500 N,铣削深度为3 mm 时达到最大值572 N,随着进给量的增加,Fx缓慢增加,直至趋于稳定;Fy随着铣削深度、转速和进给量的增加慢慢升高。铣削深度与转速同时增加Fx先增加后逐渐减小,Fy持续增加。
(3)Fx内冷铣削高于干式铣削,二者的Fy相差不大,内冷铣削加工质量高,工件Ra为0.193~0.327µm;以铣削力分量最小为优化目标,获得一组最优铣削参数:转速11 643.63 r/min,铣削深度1 mm,进给量0.08 mm/r。
