扫描式激光测径仪中电机转速波动对精度的影响及误差修正研究

段长超 彭松 谭骏 方辉

摘  要： 激光扫描测量设备中，测量精度主要取决于扫描光带的平行性以及其扫描速度是否均匀，而扫描速度的均匀性主要取决于驱动多面棱镜旋转的驱动电机，其转速波动或漂移是造成测量误差的主要原因。该研究通过在测量光路中加入尺寸已知的光阑，利用同时测量光阑和未知测量对象直径的同步测量方法来消除电机转速波动的影响，并利用非线性补偿方法进行误差修正，尽可能减小系统误差对测量误差的影响。实验验证结果表明，经以上方法优化的激光扫描测量设备测量精度达到±0.002 mm，能够满足实际应用需要。

关键词： 转速波动; 误差修正; 激光扫描; 同步测量; 非线性补偿; 高精度测量

中图分类号： TN929?34                             文献标识码： A                      文章編号： 1004?373X（2020）04?0112?05

Influence of motor speed fluctuation in laser scanning diameter measuring gauge on accuracy and its error correction

DUAN Changchao， PENG Song， TAN Jun， FANG Hui

（School of Manufacturing Science and Engineering， Sichuan University， Chengdu 610065， China）

Abstract： In the laser scanning measurement equipment， the measurement accuracy mainly depends on the parallelism of the scanning light band and the uniformity of its scanning speed， while the uniformity of the scanning speed mainly depends on the driving motor driving the rotation of the polyhedral prism， and the speed fluctuation or drift is the main cause of the measurement error. The influence of motor speed fluctuation can be eliminated by adding the apertures with known dimensions to the measurement beam， and by means of the synchronous measurement method that the diameter of the unknown measurement object and the aperture can be measured simultaneously. The error correction is performed by means of the nonlinear compensation method to minimize the impact of system error on measurement error. The experimental verification results show that the measurement accuracy of the optimized laser scanning measuring equipment can reach to ±0.002mm， which can meet the needs of the practical applications.

Keywords： speed fluctuation; error correction; laser scanning; synchronous measurement; nonlinear compensation; high?accuracy measurement

0  引  言

激光测径仪作为高精度、非接触的线性尺寸测量仪器，被广泛用于线缆、漆包线、电磁线、纤维橡胶管、玻璃管、电子元件等外径尺寸的在线检测和控制[1?2]。一维线性尺寸测径仪主要分为CCD投影式激光测径仪和扫描式激光测径仪。CCD投影式激光测径仪的测量精度和测量尺寸范围主要受到CCD芯片感光像素及尺寸大小的制约，且不适于高温大湿度场合的应用[3]。扫描式激光测径仪所用的关键光学部件[f?θ]透镜，能够将旋转扫描光束变为平行扫描光束。由于现代光学设计及光学加工工艺的进步，制作出结构简单紧凑、扫描精度高、容易加工的小焦距[f?θ]透镜难度不大，且激光束经透镜之后能在扫描测量平面达到衍射极限[4]。扫描式激光测径仪具有采样频率高、线性测量范围大等优点，且可应用于高温或辐射等恶劣环境下[5]。本研究内容基于扫描式直径测量原理，利用小焦距[f?θ]透镜进行激光束平行扫描，由光电探测器接收到的光影信号经信号处理电路、单片机的协同处理，利用同步测量和非线性补偿方法，实现了0.1～30 mm范围的直径测量，测量分辨率达到0.001 mm，测量精度为±0.002 mm。

1  扫描测径原理

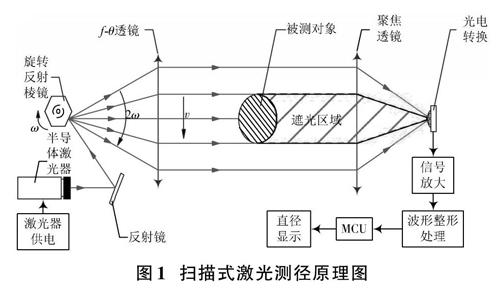
传统扫描式激光测量设备，光源通常采用He?Ne激光器或半导体激光器，单束激光定向照射旋转多面反射镜的反射面，反射镜旋转角速度为[ω]，反射光线近似从[f?θ]透镜的物方焦点处以[2ω]的角速度射入[f?θ]透镜后，形成以速度[v]匀速扫描的高速平行光线，如图1所示。平行扫描速度[v]的计算公式如下：

[v=2ωf] （1）

式中，[f]为[f?θ]透镜的焦距。

平行扫描光线经聚焦透镜汇聚于聚焦透镜的后焦点处的光电探测器上，若测量区域存在被测对象，在一定时间内光电探测器上表现为：接收光照、无光照、接收光照，其中无光照持续时间[Δt]即为被测直径的遮光时间。光电探测器产生的光电变换信号将被测对象的直径信息记录下来后，经后续信号放大及信号处理电路，将模拟电信号转换成数字信号，经MCU等处理器的处理，将直径值显示出来[6]。被测对象直径[d]的理论计算为：

[d=v·Δt]  （2）

[d=2ωf·Δt] （3）

若能提取光电探测器输出信号中扫描被测对象时的遮光时间[Δt]，结合旋转多面反射镜的角速度[ω]和[f?θ]透镜的焦距[f]，即可得到被测对象的直径值。

基于以上测量原理，本研究内容选用的激光器为可调焦距半导体激光器。多面反射镜的面数[N]决定了反射光线的角度[ψ]的覆盖范围，角度[ψ]的计算方法为：

[ψ=720°N=4πN，  N>2] （4）

由式（4）可知，扫描光线覆盖角度为90°，选用[f?θ]透镜的焦距[f]为70 mm，满足测量范围0.1～30 mm的要求[7]。

2  电机转速波动对测量精度的影响

扫描式激光测径仪的误差来源主要有电机转速波动导致的扫描速度误差、光学元器件的制造误差、多面反射镜的入瞳漂移原理性误差[8]、信号整形处理中由于信号边界裁定不准确而产生的遮光时间误差等，其中由于电机转速波动导致的扫描速度误差对测量结果的影响最为明显[9?10]。国内外报道的扫描式激光测径仪的多面反射镜的驱动电机通常为交流电机，通过采用高精度、高频率的正弦波驱动电源对交流电机供电，以达到稳定转速的目的[11]。采用交流电机，由于长时间工作发热严重，影响了交流电机的同步运转特性，使电机工作于异步状态，由此导致的测量误差可达到0.1%，无法满足高精度、高稳定性的测量需求，为此需要用其他方式解决电机转速波动对测量精度的影响。

由于交流电机存在以上缺点，故本研究选用了直流电机。直流电机的转速波动主要受电压波动的影响，若规定在0.1～30 mm测量范围内测径仪的分辨率要达到[Δd=0.001 mm]。假设其他影响测量精度的因素都为理想状态，由直径计算式（3）知，扫描电机角速度[ω]应该为一个固定值，而实际工作中电机转速存在不稳定的变化，导致电机扫描角速度[ω]存在误差[Δω]，设电机的转速为[n]，当电机转速存在误差[Δn]时，则扫描角速度的误差为：

[Δω=2πΔn]   （5）

掃描速度误差为：

[Δv=2f·Δω=4πfΔn]  （6）

对时间间隔[Δt]的测量一直为较精确的真实值，由测量计算式（2）、式（3）知，扫描分辨率[Δd]与时间间隔[Δt]的偏差[ΔΔt]关系为：

[Δd=v·ΔΔt=2fωΔΔt]   （7）

当无速度波动时，时间间隔[Δt1]为：

[Δt1=dv]   （8）

存在速度波动[Δv]时，时间间隔[Δt2]为：

[Δt2=dv+Δv]  （9）

故[ΔΔt]为：

[ΔΔt=Δt2-Δt1=-dΔvv（v+Δv）]   （10）

结合式（6）、式（7）、式（10）可得：

[Δn=-n1+dΔd]    （11）

由式（11）可知，当扫描分辨率[Δd]一定时，要达到该扫描分辨率，能够测量的直径值[d]与电机转速误差[Δn]成反比例关系。若规定测量转速为[n=3 000 r/min]，当测量最小直径值[dmin=0.1 mm]时，由式（11）可求得电机转速误差最大值为[Δnmax≈29.70  r/min];同理，当测量最大直径值[dmax=30 mm]时，可求得电机转速误差最小值为[Δnmin≈0.10  r/min]。

经过如上分析，当其他影响测量精度的条件理想时，要想达到0.001 mm的扫描分辨率，需要将转速误差控制在0.1 r/min以内，然而如此高的转速精度直流电机很难达到，由式（6）可得，最大速度误差不能超过[Δvmax≈0.088 m/s]。直流电源不可避免存在电压波动，一味地提高直流电机供电电压的稳定性只会增加成本，对精度的提高效果不显著。电机转速误差不可避免，为了提高激光测径仪的测量精度，本研究采用单扫描周期内同时测量尺寸已知的光阑和被测对象尺寸的同步测量方法，消除因电机转速波动导致的扫描速度误差。

3  电机转速误差补偿方法

3.1  硬件实现

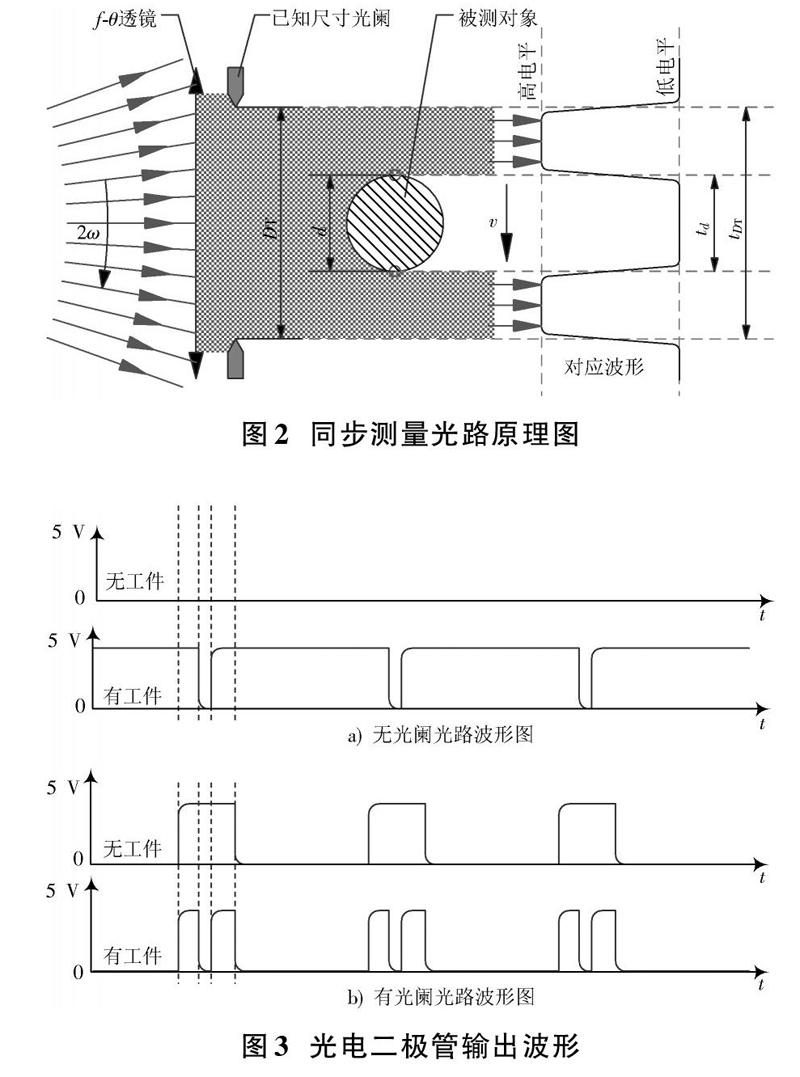
采用稳压电源模块对直流电机供电，故短时间内的电压波动无突变现象，电压变化平缓。因此可采用同步测量原理，消除速度波动对测量精度的影响。同步测量光路原理如图2所示，在[f?θ]透镜后安装一个尺寸已知的光阑，光阑尺寸满足测量范围要求，放射状扫描光线经过[f?θ]透镜后形成平行扫描光线，经光阑遮挡，形成一个宽度已知的平行扫描光带。有无光阑光路的光电二极管输出波形差异如图3所示。

扫描光束经高灵敏度光电二极管后，在时域内形成带有直径信息的电信号，经过小信号放大、波形整形处理后的信号传送到单片机，分离出带有直径信息的信号和带有光阑尺寸信息的信号，如图4所示。在FPGA内的两路计数器分别对这两路信号代表的时间宽度进行量化计数，经过SPI通信分别将时间计数值[NDT]，[Nd]发送给单片机进行数据运算处理，并通过数码管将直径测量值显示出来。因激光束平行扫描速度快，单周期在测量范围内速度可看作匀速，故两路信号的时间间隔与代表的尺寸信息成正比，如下：

[K=dDT=vΔToΔNdvΔToΔNDT=NdNDT]   （12）

式中：[d]为被测对象尺寸;[DT]为光阑间距;[To]为FPGA的晶振周期;[K]为比例系数。则被测对象尺寸可表示为：

[d=K?DT=NdNDT·ΔDT]  （13）

采用同步测量方式，同时测量被测对象尺寸与光阑间距尺寸，通过计算未知尺寸与已知尺寸的比值来求出未知尺寸，可将因扫描电机速度波动及环境温度、供电电压波动对测量精度的影响减小至最小。可通过一支标准针规直径值[dk]来校准光阑间距尺寸[DT]，如下：

[DT=K?dk]   （14）

3.2  软件设计

扫描式激光测径仪STM32单片机程序流程见图5。程序主要包括测量数据获取、数值计算、非线性补偿、数码管显示，其中测量数据获取过程由计数值通过SPI通信发送给STM32单片机，经过单片机数值计算、非线性补偿，将直径测量值通过五位数码管显示出来。

3.3  综合系统误差修正

扫描式激光测径仪由于[f?θ]透镜的加工误差、入瞳漂移、各光学元器件的装配误差等的综合影响，导致扫描光线透过[f?θ]透镜后在测量区域的扫描具有非线性[12]，表现为测量不同尺寸的标准针规时，测量值存在不同的偏差。通过测量精度为0.5 μm，直径值为0.1 mm，0.5 mm，1 mm，1.5 mm，…，29.5 mm，30 mm的系列标准针规，得到测量值数据如图6所示。测量值与标准值的关系近似为线性，如图6的X?Y2拟合曲线所示。为了直观显示测量偏差与测量值关系引入测量偏差数据，经过9次多项式拟合得到偏差值曲线X?Y1，见图6。将偏差值拟合曲线的函数加入到测量算法中实现非线性补偿。

4  实验验证与数据分析

采用同步测量方法搭建相应的实验平台，见图7。

根据《中华人民共和国国家计量技术规范?激光测径仪校准规范》（JJF 1250—2010），对实验平台进行重复性、稳定性及测量精度验证。在测量范围0.1～30 mm内选择6组标准值分别进行重复性测量，测量数据如表1所示。重复性测量实验的测量结果与真实值进行比较，得到最大示值误差为2 μm，最大相对误差不超过1%。

根据《中华人民共和国国家计量技术规范?激光测径仪校准规范》（JJF 1250—2010）对测径仪稳定性实验的要求，先开机0.5 h后，在2 h内每1 min记录1次测量数据。根据测量数据可得到以下实验结果，见图8。

根据对测径仪的重复性和稳定性试验结果可以看出，该测径仪测量值與标准值的最大示值误差不超过2 μm，能够满足实际应用的需要。

5  结  语

扫描式激光测径仪的测量精度主要受电机转速波动的影响，运用同步测量方法，同时测量已知尺寸光阑与被测对象，采用高灵活性、高运算速度的硬件架构，能实时补偿测量值，将转速、温度、电压等外界因素波动对测量精度的影响降至最低，实现了0.1～30 mm的大范围、高精度测量。实验结果表明，该激光扫描测径仪测量精度可达±0.002 mm，且测量稳定性高，结构简单，能够满足实际应用需要。

注：本文通讯作者为方辉。

参考文献

[1] 魏小龙.激光测经装置研究[D].成都：电子科技大学，2013.

[2] 王颖淑，李振辉，于晓雯.激光扫描测径仪的研究[J].长春大学学报，2004，14（4）：18?20.

[3] 吴吕宪.基于线阵CCD及STM32的滚针直径精确测量的研究[D].南京：南京理工大学，2012.

[4] 谢晋，孙晋祥，黎宇弘，等.F?Theta自由曲面透镜的精密与镜面磨削[J].机械工程学报，2016，52（17）：72?77.

[5] 李博，高艺，王红平，等.高精度PSD线性化方法与实验研究[J].长春理工大学学报（自然科学版），2013，36（1/2）：36?39.

[6] JABLONSKI Ryszard， FOTOWICZ Pawel. A new approach to the uncertainty in diameter measurement using laser scanning instrument [M]// B?EZINA Tomá?， JABLO?SKI Ryszard. Machatronics 2013. Berlin： Springer， 2014： 463?470.

[7] 陈海清.现代实用光学系统[M].武汉：华中科技大学出版社，2003.

[8] 许敏，胡家升.激光扫描成像中旋转多面体的分析计算[J].中国激光，2008，35（5）：782?787.

[9] 郭飞飞，王宝光.高精度外径激光自动测量系统的研究[J].传感器与系统，2010，29（3）：50?51.

[10] 陶雷，李新秋，张力生.扫描式激光测径技术的算法新探[J].NDT无损检测，2007，29（7）：386?388.

[11] 吴裕斌.激光扫描测量系统扫描速度不均匀的实时校正[J].华中理工大学学报，1997，25（4）：41?42.

[12] 王一，程大林，任永杰，等.透射式激光扫描测径技术[J].光电工程，2011，38（7）：64?68.