喷浆台车机械臂的静动态特性分析及拓扑优化

李若昕，姜永正, ，陆小龙，夏启航

（1.湖南科技大学 机电工程学院，湖南 湘潭 411201；2.湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201）

0 引言

喷浆台车是当前隧道、涵洞等地下建筑进行喷浆支护时的主要工具，随着现代工程建设的大规模开展，对喷浆台车的需求量大大增加[1]。现代的喷浆机械臂朝着大型化和智能化方向发展，机械臂的响应快速性和稳定性是一个很重要的设计要求[2]。又因为地下建筑的施工环境较为恶劣，机械臂的俯仰运作频繁，机械臂受力情况复杂，导致机械臂在运作过程中易开裂，对施工人员的生命安全造成威胁[3]。为保证施工人员的生命财产安全，提高施工效率，延长喷浆台车机械臂的使用年限，对喷浆台车机械臂的分析研究显得十分必要。

据调查了解，在大部分工厂中，他们对于机械臂开裂问题的解决方法多是对开裂处进行加厚处理，这解决了一时的开裂问题，但是未从机械臂强度等方面对机械臂本身的缺陷进行分析，加厚的机械臂后期仍然会出现问题，故这种解决方法治标不治本[4]。在航天、航空、汽车等高科技工业领域中，面对臂管开裂的情况，设计者广泛应用拓扑优化这一优化方法加以解决。如S.Mantovani 等[5]对汽车的仪表板进行了拓扑优化，最终设计出了一款高性能跑车仪表板；M.Imran 等[6]对飞机起落架进行有限元分析，并对飞机起落架结构进行了合理的改进。

综上所述，拓扑优化能够在材料均匀分布的设计空间中找出最佳的分布方案[7]，并且能够为实物的优化改进设计提供良好的理论基础。但是在传统的工业领域中，拓扑优化的运用却略显匮乏。因此本文以喷浆台车机械臂作为研究对象，且为了研究静态情况下以柔度为目标函数的机械臂拓扑结构，建立了机械臂的有限元模型，利用美国Altair公司HyperMesh系列软件中Optistruct 对机械臂单独进行有限元分析，并通过对比有限元仿真模拟实验[8]结果，对机械臂进行了简单的拓扑优化分析。并通过拓扑优化所得结果对机械臂进行了改良，分析结果对比证实该优化取得了良好的效果。

1 现有机械臂建模及特性分析

1.1 机械臂有限元模型

喷浆台车大臂的结构组成见图1。

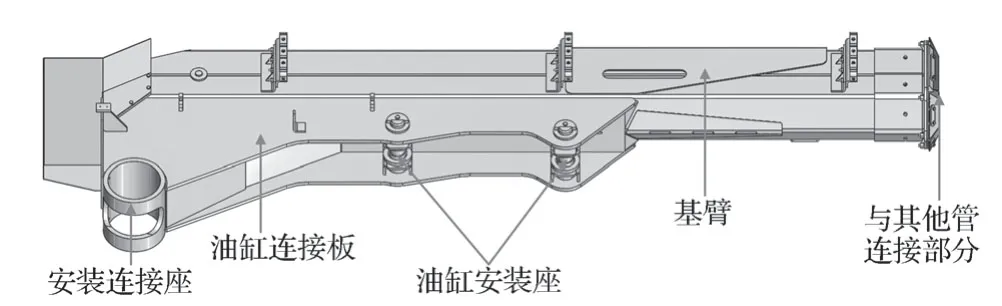
图1 喷浆台车机械臂大臂结构示意图Fig.1 Schematic diagram of large arm structure of shotcreting trolley

如图1所示，喷浆台车机械大臂可分为臂管、安装座连接轴和两个油缸安装座。机械臂具体型号为GL3515，其施工能力为35 m3/h。

由于喷浆台车大臂结构复杂，主要由各种厚度的钢板焊接而成。为简化计算，只取喷浆台车机械臂大臂的主要臂管部分进行有限元分析。其中测得喷浆台车机械臂大臂的基臂长3 306 mm，宽274 mm，厚度为6 mm；油缸连接板长约2 180 mm，两板间相距226 mm，板厚16 mm；油缸安装座长120 mm，宽226 mm，板厚10 mm；安装连接座半径120 mm，板厚20 mm；与其他管连接部分长208 mm，宽274 mm，板厚14 mm。在HyperMesh中建立其有限元模型，如图2所示。

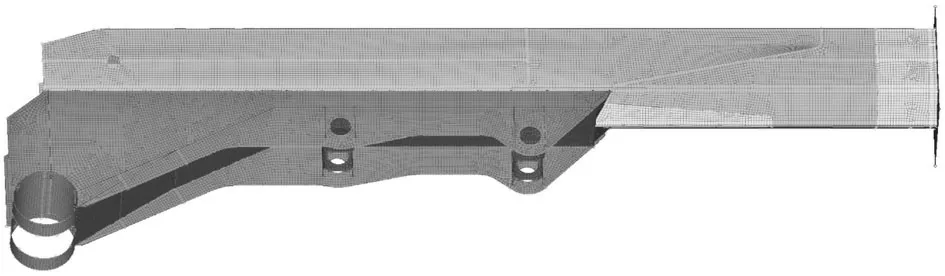
图2 喷浆台车机械臂有限元模型Fig.2 Finite element model of the shotcreting trolley mechanical arm

课题组主要使用shell单元对大臂基臂进行离散，对安装座连接轴、两个油缸安装座以及右端杆连接部分结构用rigid单元进行模拟。机械臂大臂的材料为HG70高强度焊接结构钢，其化学成份如表1所示。

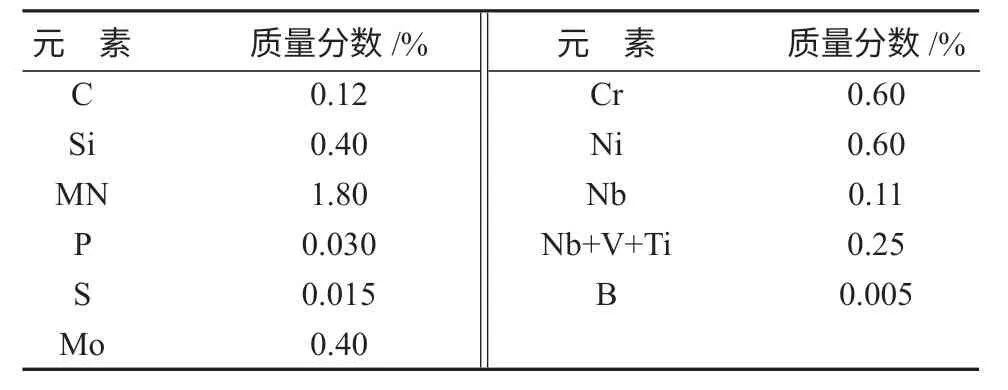
表1 HG70高强度焊接结构钢化学成份Table1 Chemical composition of HG70 high strength welded structural steel

HG70高强度焊接结构钢的力学性能指标如表2所示。

表2 HG70高强度焊接结构钢力学指标Table2 Mechanical indexes of HG70 high strength welding structural st eel

该材料的密度为7 850 kg/m3，弹性模量为200 GPa，泊松比为0.3。经过测量，得出原喷浆台车机械臂总体积为5.554e+07 mm3。由“质量=密度×体积”公式可得，原机械臂的质量为：7 850 kg/m3×5.554e+07 mm3≈436 kg。

1.2 刚强度分析

图3所示为机械大臂在工作过程中的受力情况示意图。

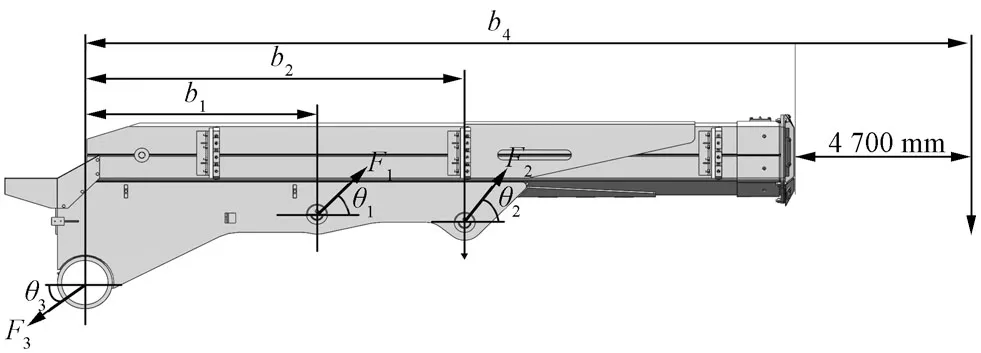
图3 机械臂受力情况示意图Fig.3 Schematic diagram of mechanical arm under force

机械大臂受到两个斜向上的支撑力F1、F2，一个斜向下但方向不定的力F3，以及一个垂直向下的力F4的作用，在4个力的共同作用下，大臂保持平衡。以点A为基点，对大臂进行受力分析，可得：

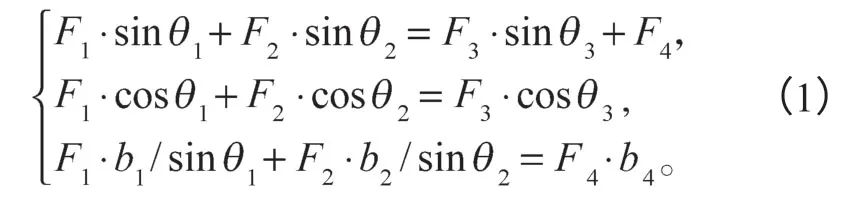
根据实际情况和计算要求，对机械臂建立一个工况。在安装座连接轴所在面和两个油缸安装座所处圆孔处进行全方位约束。在大臂右侧与机械臂其它臂管连接部分的不规则孔处建立rigid单元，将rigid单元沿x轴方向刚性平行移动4 700 mm，考虑到动载系数，于是在rigid单元上施加一个沿y方向向上的、大小为19 500 N×1.2倍的力。

通过计算求解得出该工况下的机械臂应力分布如图4所示，其中图b是对图a中应力最大部分的放大细节。

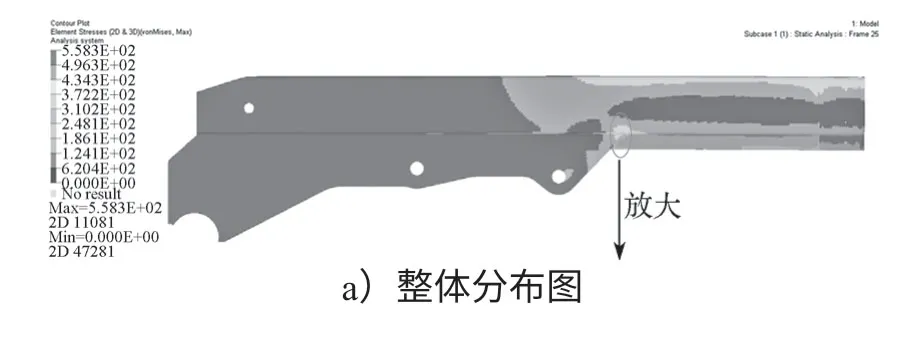
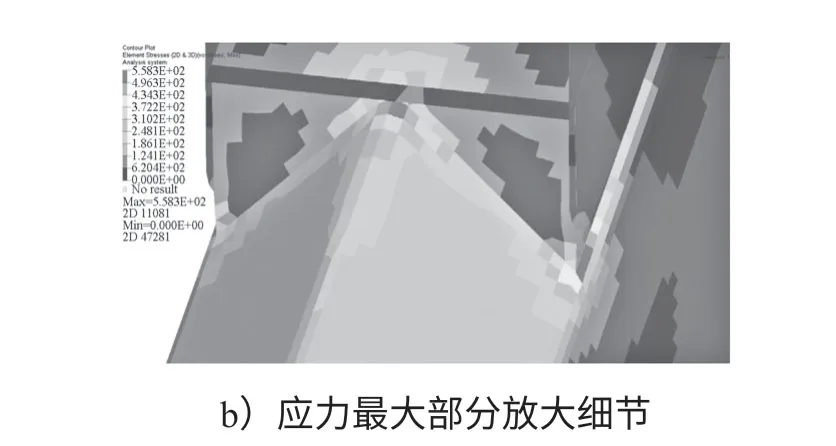
图4 原机械臂应力分布图Fig.4 Original mechanical arm stress distribution diagram

由图可见，原机械臂所受应力最大部分主要集中在基臂和油缸连接板的接合处，最大应力达到了558.3 MPa，而油缸连接板部分所受应力很小，应力分布极其不均，因此对其进行拓扑优化很有必要。

1.3 模态分析

模态分析[9-10]是研究物体动力特性的一种方法，其中模态是指物体机械结构的固有振动频率。其矩阵表达式为

其对应的特征方程为

式（2）（3）中：M为结构质量矩阵；

K为刚度矩阵；

ω为自由振动固有频率。

求解出方程（2）即可求出系统的固有频率和振型。由于单纯机械激励频率[11]多在10 Hz 以内，在Optistruct中对机械臂进行模态分析，根据需要提取前6阶模态结果，前6阶模态频率如表3所示。

表3 机械臂大臂的前6阶频率Table3 First 6 frequencies of the big arm of the manipulator arm

第1、3、4、6阶模态的振型如图5a～d所示。由图可知第1阶模态固有频率为81.23 Hz，振型由左右摆动为主；第3阶模态固有频率为152.76 Hz，振型由上下摆动为主；第4阶模态固有频率为170.67 Hz，振型由整个机械臂振动，带动机械臂大臂与其他管连接部分上下摆动；第6阶模态固有频率为179.55 Hz，振型由机械臂基臂靠近安装连接座部分局部左右摆动。

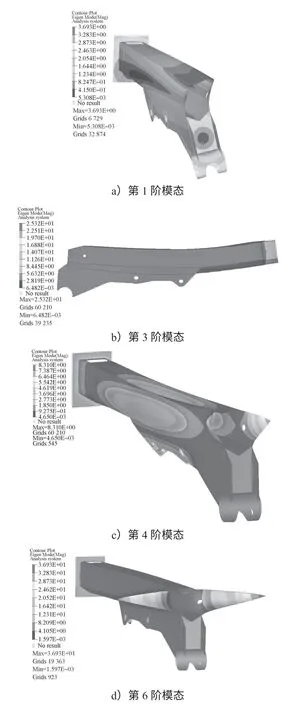
图5 原机械臂模态分析图Fig.5 Original mechanical arm modal analysis diagram

2 机械臂拓扑优化

2.1 目标与约束条件

拓扑优化是一种根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化的一种结构优化方法。拓扑优化相较于尺寸优化和形状优化，具有更多的设计自由度，从而能获得更大的设计空间。

优化过程的数学模型如下。

设计变量：

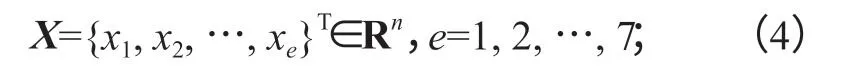
目标函数为

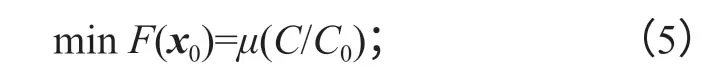
状态变量为：

式（4）～（6）中：Rn为一个n维实欧氏空间，称为设计空间；

C0为进行刚度优化时的最初拓扑值；

μ为权系数，取值区间为[0,0.1]；

V(x)为机械臂油缸连接板的设计部分的体积分数。

课题组在对机械臂进行工况处理时，在有限元模型上对安装座连接轴所在面和两个油缸安装座所处圆孔处进行全方位约束。在大臂右侧与机械臂其他臂管连接部分的不规则孔处建立rigid单元，将rigid单元沿x轴方向刚性平行移动4 700 mm，并施加一个沿y方向向上的19 500 N的力。以该工况下大臂柔度最小作为优化目标，以油缸连接板体积不超过原大臂总体积的0.2，且机械臂所受应力小于500 MPa 作为约束条件。在机械臂的尺寸优化中，以臂管厚度作为设计变量，在Hypermesh中，将机械臂的臂管按照所处位置及初始厚度分为7个组件。在Optistruct软件中用0阶方法进行优化计算，经过10次迭代计算后得到优化结果。

2.2 优化结果

经过10次迭代计算后的优化结果如图6所示。

图6 原机械臂10次迭代后的拓扑优化图Fig.6 Topology optimization diagram after ten iterations of the original manipulator

图6为单元密度分布图，图中油缸连接板内侧部分单元密度值较低，说明此部分材料分布较为富余，在机械臂形貌的重新设计中，可以删去以减轻机械臂的质量。与原机械臂相比，油缸连接板侧板处有较大不同，原油缸连接板上部分不必要的筋板被删除，原来的4 块面板也变成了一块面板加4 块小三角形筋板的形式。

3 拓扑结构重设计及性能对比

3.1 结构重设计

由于拓扑优化完之后，以删除单元为形式，导致大臂表面不光滑，或某些地方不连续，所以需要进行平整化处理。根据形貌优化后的结果对机械臂大臂进行重新设计，优化前后的机械臂结构对比图如图7所示。

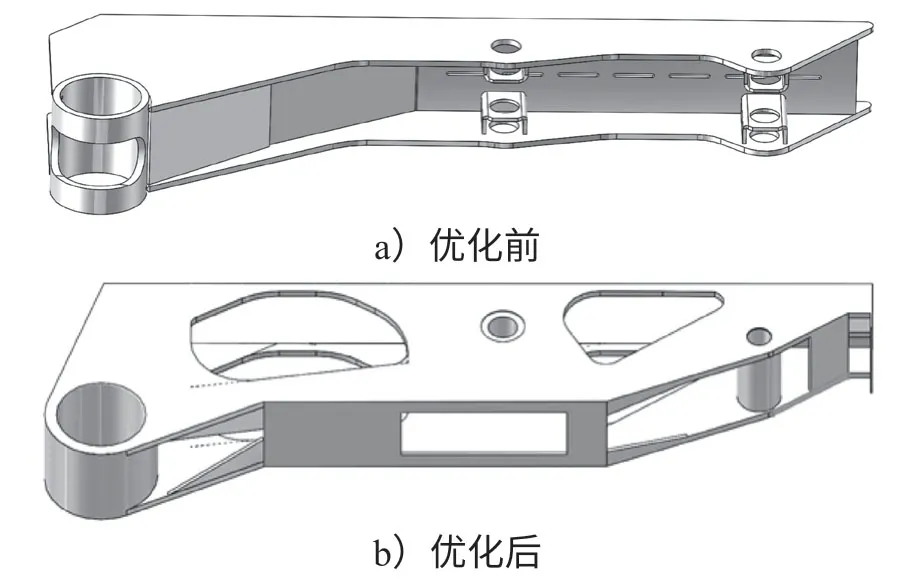
图7 优化前后机械臂模型结构Fig.7 Model structure of the manipulator before and after optimization

由图7可清晰看出机械臂优化前后油缸连接侧板及3 块面板的变化，删去了油缸连接板侧板处不必要的筋板，将3 块面板减少成1 块面板加4 块小三角形筋板的形式。

通过测量机械臂优化前后的总体积，算得：

优化前机械臂质量为7 850 kg/m3×5.554e+07 mm3≈436 kg；

优化后机械臂质量为7 850 kg/m3×5.091e+07 mm3≈399 kg。

机械臂的质量由原来的436 kg 减少到399 kg，降幅超过8%，使机械臂结构更合理，同时也降低了制造成本。

3.2 优化前后性能对比

对优化后的机械臂进行静力学和模态分析。优化后机械臂的最大应力由初始的553.8 MPa 减小到503.7 MPa，并且受力比原来更均匀。优化后机械臂的前6阶模态如表4所示。

表4 优化后机械臂大臂的前6阶频率Table4 First 6 frequencies of the robot arm after optimization

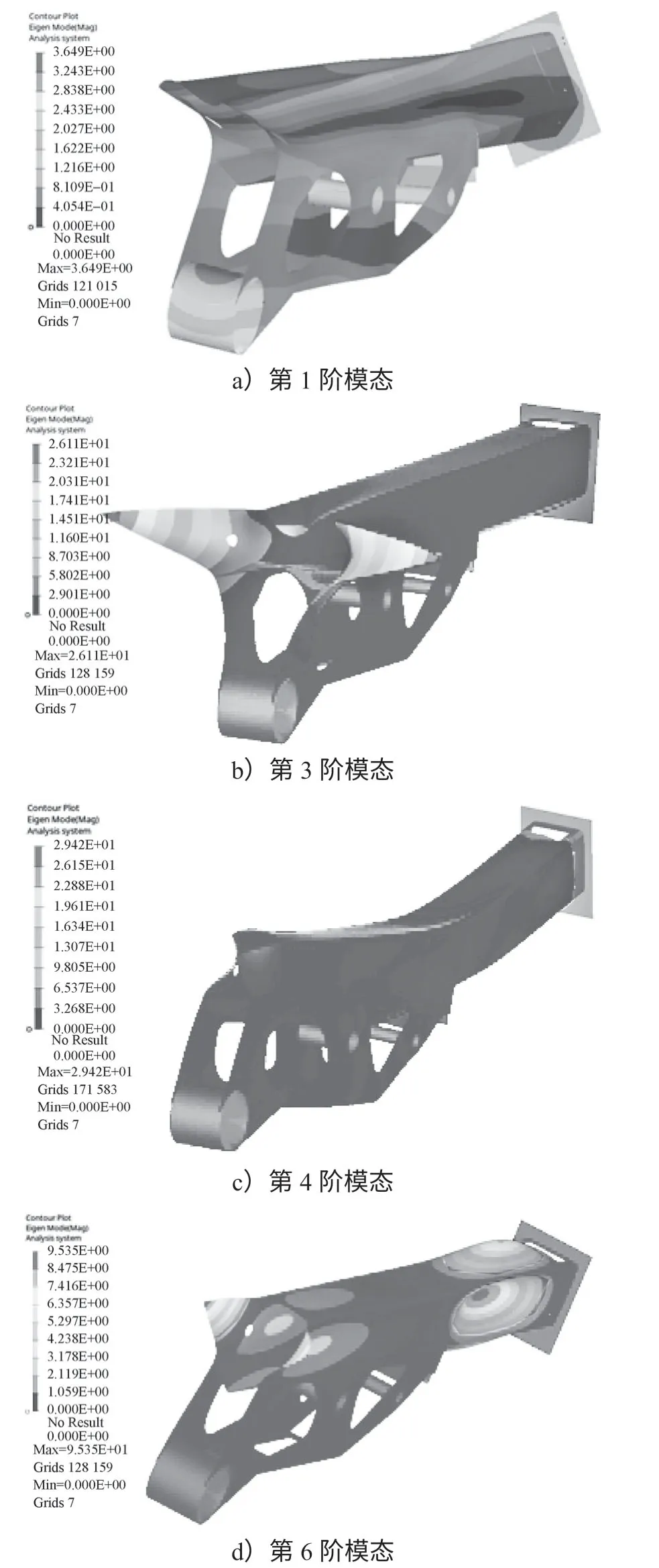
图8 优化后机械臂模态分析图Fig.8 Modal analysis diagram of the optimized manipulator

优化后的机械臂的模态分析图如图8所示。

由图8中的4张图可清晰看出第1、3、4、6阶模态的振型。对比表3和表4可以得出，机械臂的频率及振型都有较大的变化。从理论上来说，固有频率2=刚度/质量,增加刚度会提高固有频率。优化前后的机械臂固有频率对比如表5所示，由表中数据对比可见新机械臂的第一阶弹性模态固有频率由原来的81.23 Hz 提高到89.09 Hz，固有频率的提高代表着机械臂整体结构刚度得到了提升。提升机械臂的刚度能减少机械臂的变形和应力，从而对结构起到较好的保护作用。

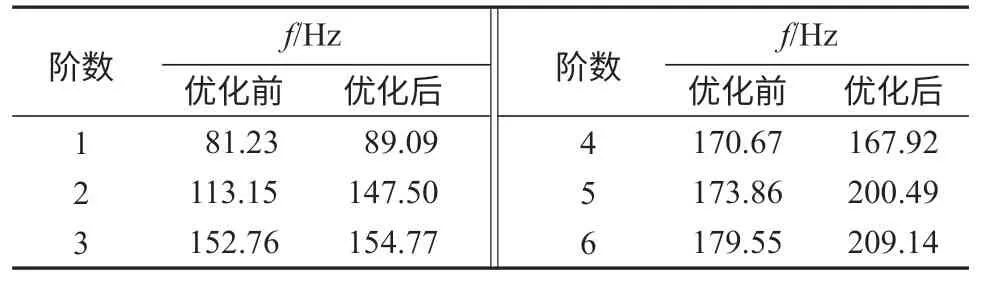
表5 优化前后机械臂大臂的固有频率Table5 Natural frequency of the manipulator arm before and after optimization

优化前后机械臂所受应力大小如图9所示。对比优化前后两图可以得出，机械臂的最大应力由553.8 MPa 减小到503.7 MPa，原机械臂所受应力最大部分主要集中在基臂和油缸连接板的接合处，经过优化后的机械臂所受应力最大部分集中于基臂上，并且受力比原来更均匀。

图9 优化前后机械臂所受应力大小对比图Fig.9 Comparison diagram of stress on mechanical arm before and after optimization

4 结语

本文建立了针对喷浆台车机械臂大臂的有限元模型，并对其进行了静态模态分析和拓扑优化。以柔度最小为优化目标，优化后的新机械臂质量减少了37 kg，减少了约8%的质量。第一阶弹性模态固有频率由81.23 Hz 提高到89.09 Hz，最大应力在规定工况下降低9%。综上可看出，喷浆台车机械臂大臂结构综合静态性能得到了较大的改善，为后期喷浆台车机械臂的优化设计提供了理论基础。