如何正确运用t检验
——两几何均值比较一般差异性t检验及SAS实现
2020-07-23于泽洋刘媛媛李长平胡良平
于泽洋 ,刘媛媛 *,李长平 ,2,胡良平
(1.天津医科大学公共卫生学院,天津 300070;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029;3.军事科学院研究生院,北京 100850
t检验主要用于样本含量较小,总体标准差未知的正态分布。单从均值比较的角度看,t检验主要用于以下三种实验设计条件下一个定量评价指标算术均数的比较,即“单组设计”“配对设计”和“成组设计”。t检验因其所需样本含量小、计算简单及检验功效较高而成为广大科研工作者最为熟悉且应用最多的统计分析方法之一[1-2]。本文主要介绍几何均数以及两组近似对数正态分布数据几何均数的一般差异性t检验及SAS实现。
1 基本概念
1.1 几何均数及其计算公式
在临床医学研究中,一些变量的数值往往并不呈对称分布,有时会遇到呈等比(即倍数)关系的计量数据或计数数据,例如大气中某成分的浓度指标,临床血清学诊断的抗体滴度数据等。由于这类数据往往不符合正态分布而呈正偏态分布,在进行统计描述时,不能直接通过算术均数和算术标准差来描述其数据的集中趋势和离散程度。但这样的数据经过对数变换(即取对数)后往往呈近似正态分布,被称作服从对数正态分布的数据,此时该变量的对数值的平均水平可以用算术均数来表示,见式(1):


对于以频数分布表形式给出的数据,同样可以用组中值xMi估计对应组段中各个观测值的大小,得到几何均数的近似计算公式如下:
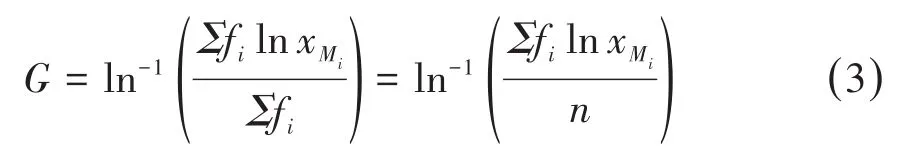
与几何均数相比,算术均数的计算相对简便,是应用最为广泛的平均数指标。但算术均数对于特大或者特小的观测值十分敏感。如果数据呈偏态分布,直接计算出的算术均数往往会偏向拖尾一侧,不能很好地反映全部观测值的平均水平。因此,算术均数主要适用于描述不含极端值的对称分布变量的平均水平。几何均数适合于原始数据呈正偏态分布但经对数转换后呈近似对称分布的数据,尤其是医学研究中遇到的呈现等比例变化的数据,如抗体滴度、血清凝集效价等[3]。几何均数的对数值实际上是各变量值对数的算术均数。并且,几何均数受极端值的影响比算术均数小。但几何均数在计算时,变量值中不能有零值或者负值。
2 问题与数据结构
【例1】在一项对精神分裂症患者血脂水平与奥氮平血浆浓度之间关系的研究[4]中,研究者选取患者24人,根据2007年中国成人血脂防治指南推荐标准分为高脂血症组和血脂正常组,假设测定的患者奥氮平血浆浓度如下(单位为ng/mL),高脂血症组:x1=40,20,30,25,10,15,25,30,40,10,15,80;血脂正常组:x2=11,87,42,15,20,16,23,10,35,70,95,75。试分析两组受试者奥氮平血浆浓度之间差异是否有统计学意义。
该例整体数据涉及两个组,每组有12个观测值,共24个观测值,样本量较小,测量指标为“药物血浆浓度”,数据所取自的实验设计类型属于“成组设计”,该资料的完整描述为“成组设计一元定量资料”。
该研究是考察两组总体均数之间差异是否有统计学意义,且主要评价指标为药物血浆浓度,由于同一组数据内部各数据之间呈现近似倍数关系,故宜选用几何均数G表示其平均水平,因此,应该对几何均数G的差异性进行统计分析。若进行对数变换后,定量资料满足独立性、正态性和方差齐性的条件,可对其进行成组设计一元定量资料t检验,此时,还可以求出每组该定量指标的总体平均值的95%置信区间,再取反对数,即可得到原始数据的平均值的置信区间;否则,应该直接对原始数据进行符号秩和检验[5]。
3 SAS程序及结果解释
3.1 SAS主要程序


【程序说明】本示例SAS程序共4步,包括2个数据步和2个过程步。第1个数据步先建立数据集G_mean,利用input语句输入变量nd(血浆药物浓度)、group(不同患者类型的分组,组1为高脂血症组,组2为血脂正常组);第2个数据步调用log函数,取药物血浆浓度值以e为底数的对数值,定义为新变量y;第3步调用UNIVARIATE过程,通过添加NORMAL选项对原始数据药物血浆浓度nd以及对数值y按照不同分组进行正态性检验,分组变量为group;第4步为t检验,调用TTEST过程,对变量y按照分组变量group进行一般差异性t检验。选项COCHRAN表示输出COCHRAN近似t检验的结果。
3.2 主要输出结果及解释

以上为正态性检验的结果,由于本例中样本例数较少,所以参考Shapiro-Wilk检验的结果,可知两组原始数据(变量为nd)不服从正态分布(W=0.812115、0.853688;P=0.0129、0.0408,P均<0.05),而经对数变换后的数据(变量为y)符合正态分布(W=0.957749、0.91446;P=0.7513、0.2433,P均>0.05)。
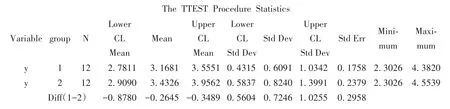
以上均为变量y的基本描述统计量,由输出结果可知,高脂血症组变量y的均值为3.1681(95%CI:2.7811~3.5551);标 准 差 为 0.6091(95%CI:0.4315~1.0342);标 准 误 为 0.1758;最 小 值 为2.3026,最大值为4.3820。血脂正常组变量y的均值为 3.4326(95%CI:2.9090~3.9562);标准差为0.8240(95%CI:0.5837~1.3991);标 准 误 为0.2379;最小值为2.3026,最大值为4.5539。


以上为t检验和方差齐性检验的输出结果,由检验两组方差齐性的结果,可知两总体方差相等(F=1.83,P=0.3307>0.05),所以本例经对数变换后的数据满足独立性、正态性和方差齐性的条件,可以使用成组设计的一般差异性t检验进行均数比较,t=-0.89,P=0.3809>0.05,尚不能认为两均值之间差异有统计学意义。
两组原始数据经对数变换后的y值的平均值分别为3.1681和3.4326,对这两个均值取反对数(即进行指数运算)后,可以得到原始药物血浆浓度数据的平均值,即几何均数G,G1=e3.1681=23.76,G2=e3.4326=30.95。由此可以下结论,两组药物血浆浓度的几何均数分别为:高脂血症组23.76 ng/mL,血脂正常组30.95 ng/mL,且两组均值差异无统计学意义,尚不能认为高脂血症患者药物血浆浓度明显低于血浆正常组。
4 讨论与小结
算术均数和标准差是描述正态分布计量数据集中趋势与离散程度的两个统计量,而几何均数是用于描述对数正态分布计量数据集中趋势的统计量,其区别在于:算数均数与算数标准差描绘的是算术度量上的集中与离散,而几何均数描述的是几何(倍数)度量上的集中趋势。因此,在对近似服从对数正态分布的定量资料进行分析时,要对数据的分布情况进行判断后再选择合适的描述方式,例如原始数据不能有负值或零值(必要时,可以给每个原始数据都加上同一个正数,并确保不会再出现负值或零值,这样做在数学上被称为平移变换,不会改变结果的正确性),对原始数据进行对数变换后再使用t检验,仍应进行正态性检验和方差齐性检验。需要注意的是,取对数之后求得的均数要经过取反对数才是原始数据的几何均数。
由于不同类型数据的特征不同,在分析之前的预处理也不同,部分原始数据不一定通过简单的取对数变换就一定能满足正态性要求,还需要更加复杂的变换,例如有时需要进行log(X+K)或log(KX)变换(K为某一常数,通过尝试确定)或Box-Cox变换才呈正态,需要根据具体数据确定[6-7]。
