基于复杂系数的软件可靠性分配方法研究

杨婷 贾岚 原变青

摘要：随着计算机软件技术的发展，软件规模及软件功能也在不断扩充，在软件系统的设计和开发过程中，如何确保所开发的软件系统能够满足既定的可靠性指标，软件可靠性分配技术则是其中必不可少的环节。该文分析了可靠性分配的原理，给出了在进行软件可靠性分配时，应遵循的原则以及分配的步骤，在此基础上，给出了基于McCabe软件复杂性的间接度量，为后续进一步迭代分配软件可靠性提供依据。

关键词：软件可靠性分配;软件复杂度;McCabe度量、复杂系数

中图分类号：TP311 文献标识码：A

1概述

随着计算机软件技术的发展，软件规模及软件功能也在不断扩充，软件系统的结构也越来越复杂，在计算机系统的实现过程中，由软件实现的功能所占比例也不断增加，同时，由软件失效导致系统失效的次数也远超过硬件所导致的系统失效次数。因此，如何确保所开发的软件系统能够满足既定的可靠性指标，使软件既能保证进度要求，又能降低生产成本，是当前软件可靠性工程中要解决的一个重要问题。在软件可靠性工程的设计和开发阶段，首要任务则是在各功能模块或组件之间完成可靠性指标的分配任务。

本文分析了可靠性分配的原理，给出了在进行软件可靠性分配时，应遵循的原则以及分配原理，在此基础上，给出了基于MaCabe软件复杂性的間接度量，为后续进一步迭代分配软件可靠性提供依据。

2软件可靠性分配原则及分配步骤

2.1分配原则

在软件可靠性工程中，软件可靠性分配过程和软件可靠性预测过程正好相反，可靠性预测是一种合成方法，即：从底向上逐步完成系统指标的计算和评估，而可靠性分配过程则是一种分解方法，即：从顶向下逐层完成系统指标的分解和分配，根据初次分配的结果，搞清楚分配的指标与预测值之间的差距，进一步采取一定的措施加以修正。

因此，在进行软件可靠性指标分配时，需遵循如下两个原则：

1）要保证满足系统可靠性要求;

2）要平衡设置各模块或部件的可靠性指标。

针对第2）条原则，需要注意两点，一是在每个部件或模块的设计和开发过程中，要综合权衡时间、难度、风险、重要度等因素的差距;二是要使整个系统的开发成本最低。

2.2分配步骤

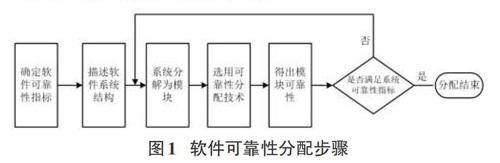
软件可靠性分配是一种从顶向下逐层分解的过程，以下给出软件可靠性分配步骤，如图1所示。

1）确定软件可靠性指标：软件系统的可靠性指标是软件系统在特定的环境（条件）下，在给定的时间内，不发生故障的工作的概率，即可靠度R，除可靠度指标外，分配的指标也可以是故障率，或系统的MTBF（故障平均时间间隔）。

2）根据系统需求规格说明书，找出软件的剖面及边界。

3）按照功能说明，在考虑系统的结构特性以及收集的历史数据的特性（如存在哪些可靠性已知的类似模块），将系统自顶向下分解为不同的部件或模块。

4）选用一定的数学模型分配给整个系统，确定了整个系统的可靠性指标后，再根据具体功能和影响因子具体分配给部件或模块。

5）根据初次分配的结果，搞清楚分配的可靠性指标与预测值之间的差距，进一步采取相应的措施加以修正。

3基于MaCabe软件复杂性的间接度量及可靠性分配

3.1软件复杂性的McCabe间接度量

软件复杂性主要体现现在程序的复杂性上，软件越复杂，在开发和维护过程中所消耗的资源也越多。因此，软件的复杂性可以作为软件所需资源投入量的一个间接度量。此外，软件越复杂，在设计中出现错误的可能性也越大，这是一种合乎逻辑的推理，尽管复杂性与软件中的错误数未必呈现出简单的正比关系，但是存在这种正相关趋势则是肯定无疑的。

本文给出McCabe复杂性度量方法，并以此作为复杂性因子，给出了基于复杂性因子的分配方法，为后续进一步迭代分配软件可靠性提供方法依据。

软件复杂性的度量可以从执行程序指令以及结构关系来研究。

以下考虑程序指令间的相互关系，即结构上的错综程度，来研究程序结构的复杂性。

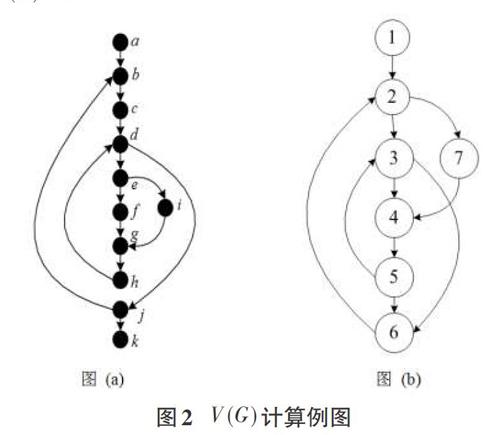
将程序中的每个处理步骤和判定符收缩为一个点，将有关的点用线段连接起来，就得到抽象的程序流图。有向图中从某一节点出发的路，如果最终又回到原来的节点，则称这样的路为回路。如果在有向图中，任意一个节点至少可以找出一条路通向其他任意的一个节点，这样的有向图称为强连接有向图。

用V（G）表示有向图中的回路数，用m表示图中的弧的数目，n表示节点数，对于强连接的有向图，若用回路数V（G）来表示其复杂性，则可以证明V（G）由下列公式给出：

V（G）=m-n+1

上式称为程序的循环性度量，又称为McCabe复杂性度量。如图2所示，图（a）和图（b）都表示程序流图，按上式计算得：

V（G）=13-11+1=3

图（b）按上式计算得：

V（G）=10-7+1=4

上面的方法同样可以度量程序的循环结构，通常，循环结构复杂的程序，往往出错率也会高。通过比较上面的两个程序流图，可预知图（b）隐含的错误数大于图（a）所含错误数。

3.2基于复杂性系数的软件可靠性分配方法

本节将给出基于复杂性系数的软件可靠性分配方法，该方法将系统失效率分配到各个模块中。若某一部件或模块的复杂系数越大，那么为达到一定的可靠性而花的维护费用也越大，因此，该模块或部件所分配的失效率也将越高。

以下给出具体的分配步骤：

1）确定软件系统总的失效率。

2）确定模块数M。

3）确定每一部件或模块的复杂性因子wi。

4）确定每一部件或模块实际运行的时间ti，以及任务的时间T。

5）计算失效率的调整系数：

4结束语

软件可靠性分配方法与硬件可靠性分配方法相比，模型的选择和分配的灵活度都存在差异。已知的软件可靠性分配方法很多都借鉴了硬件可靠性的技术，同时考虑了软件自身的特点和性质，进而形成了符合软件特性的软件可靠性分配方法。本文给出了基于McCabe软件复杂性的间接度量，为进一步迭代分配软件可靠性提供依据，后续可以进一步研究基于复杂性、重要度以及调用强度等因素的可靠性分配技术。