解耦理论在计算发动机拉杆悬置刚体模态中的应用

李长华 向焕东 张鹏

摘 要：以解耦理论为基础，建立了以拉杆悬置为系统的计算模型，量化评估了拉杆悬置等效质量改变带来的刚体模态频率的变化，通过实验验证，解决了样车调教过程中一种由拉杆悬置刚体模态引起的加速轰鸣问题。

关键词：加速轰鸣;拉杆悬置;能量解耦;刚体模态

汽车舒适性要求越来越高，相对应的悬置系统就承担着更加重要的角色。本文基于解决一种发动机拉杆悬置引起的加速轰鸣[1-2]问题，以解耦理论为基础，量化计算拉杆悬置刚体模态，解决了该车加速轰鸣，提高该车型的舒适性。

1 问题的提出及解耦计算方法

1.1 拉杆悬置与发动机悬置系统

乘用车横置动力总成的悬置系统几乎都是采用三点式悬置布置，即左悬置、右悬置和拉杆悬置，悬置系统在整车中的位置如图1所示：

本文重点探讨悬置系统中的拉杆悬置，及其模态特性引起的NVH问题。由拉杆悬置刚体模态引起的车内加速轰鸣声具有声压级高、声品质影响大等特点，其成因一般是发动机二阶频率激励起拉杆悬置Z向刚体模态，引起拉杆悬置共振起放大作用，振动再经过副车架传递到车身，通过车身传递到乘员舱引起车内轰鸣，该轰鸣问题与发动机振动的大小无关，与悬置系统的隔振性能无关，只与激励频率和拉杆悬置本体模态特性相关[3-5]。而激励频率无法改变，因此获得拉杆悬置本体的模态特性即是解决问题的关键点。故本文不讨论发动机系统的振动问题，也不从整个悬置系统的角度展开，而是针对拉杆悬置本体的模态特性，提供一种量化计算拉杆悬置模态特性的思路，并应用到工程问题的解决当中。

1.2 拉杆悬置的振动模态

拉杆悬置的结构如图2（a）所示：

将拉杆悬置视为系统，两端的橡胶衬套视为橡胶元件，振动体质量为m kg（铸铝支架与两个衬套外圈质量之和），建立力学模型如图2（b）。根据参考文献[6-10]，因系统阻尼較小，不考虑系统阻尼，则系统的自由振动微分方程为：

为部件的惯性矩和惯性积，m为振动体质量，为铸铝支架与两个衬套外圈质量之和;K为系统动态刚度矩阵，与各橡胶元件的动刚度和安装角度有关，;式中，为橡胶元件在自身坐标下的动刚度矩阵。

为振型的第个元素;为振型的第个元素;为质量矩阵第行列元素。

根据式（2）（3）可以得到拉杆悬置的固有频率和阵型，进一步识别出问题方向的频率（即拉杆悬置该方向的刚体模态频率）。

2 刚体模态计算实例及验证

某车型样车调教过程中，发现在3档急加速时3200RPM左右存在加速轰鸣（测点：车内驾驶员右耳），如图3所示（实线为噪声总量，点化线为二阶曲线），并进一步分析得出此加速轰鸣是由发动机2阶引起，频率为105Hz左右。

对拉杆悬置进行频响测试，结果显示拉杆悬置本体Z向存在99Hz模态频率，如图4所示，与问题频率105Hz接近，而其他系统没有发现相近的模态频率，故怀疑问题与拉杆悬置相关。再通过手工方案验证，拉杆悬置上加质量块后轰鸣消失，确定加速轰鸣是由拉杆悬置Z向刚体模态（后文简称Z向频率）与动力总成激励频率耦合引起。其传递路径为：发动机激励-拉杆悬置-副车架-车身-乘员舱，最终引起乘员舱轰鸣。

2.1 制定方案

由于项目开发进度和成本，从源头和终端解决该问题显然不合理，故选择从传递路径解决问题。其主要思想是避频，即将拉杆悬置Z向频率的设置区间调整，问题频率为105Hz左右，根据经验，避频20Hz以上就能够达到较好的效果。

由于拉杆悬置的设计方案和悬置本身的产品特性，可以通过改变等效质量、橡胶刚度等办法改变其Z向频率，或者增加动力吸振器来解决加速轰鸣[6]。在实际工程应用中，几种方向的方案都各有优缺点[7-12]。通过沟通发现本文车型供应商产品库中有与铸铝支架相近尺寸、材料为钣金的产品，微调后即可应用。因此选定增加等效质量的方向，制定以钣金焊接支架来替代铸铝支架的方案。下一步则需要量化拉杆悬置刚体模态的变化。

2.2 仿真计算

2.2.1 解耦计算基础参数[13]辨识

拉杆悬置的惯性参数：通过CATIA软件赋予零部件对应的材料属性，测得其惯性参数（不包含两个衬套的芯子和橡胶）：Ixx 9.5E-004 Kg*m^2，Iyy 3E-003 Kg*m^2，Izz 3E-003 Kg*m^2，Ixy 3.27E-006 Kg*m^2，Iyz 2.4E-013 Kg*m^2，Iyz -1.3E-010 Kg*m^2;质心坐标：Xc 87.2mm，Yc -56.5mm，Zc -69.6mm;质量： 0.762kg。

橡胶元件弹性位置和刚度：可以从悬置系统计算报告中获取。大衬套位置：Xb 118mm，Yb -56.5mm，Zb -69.6mm;小衬套位置：Xs -5mm，Ys -56.5mm，Zs -69.6mm;大衬套动刚度：Kbu 260 N/mm， Kbv 510N/mm，Kbw 227 N/mm;小衬套动刚度：Ksu 1358N/mm， Ksv 784N/mm， Ksw 1333N/mm。

安装角度：拉杆悬置的安装角度与整车平行，即安装角度都为0°。

2.2.2 adams解耦模型建立

本文用adams软件建立拉杆悬置的解耦模型：用box体模拟拉杆悬置支架属性，用bushing单元模拟橡胶衬套属性，用bushing单元将box体和地面连接模拟拉杆悬置的安装状态，建立模型如图5所示：

2.2.3 计算结果

原方案解耦结果如表1所示：

改进方案的解耦计算参数：改进方案是将拉杆悬置的铸铝支架更换为钣金支架，其他构件不变，基础参数只有惯性参数不同。但钣金支架不同的结构对应不同的惯性参数，计算后最终选定方案的惯性参数为，Ixx 1.0E-003 Kg*m^2，Iyy 4E-003 Kg*m^2，Izz 4E-003 Kg*m^2，Ixy -1.26E-005 Kg*m^2，Iyz -4.44E-012 Kg*m^2，Ixz 5.06E-010 Kg*m^2;质心坐标：-84.1mm，-56.5mm，-69.6mm;质量：1.412kg;计算结果如表2所示：

2.2.4 解耦结果辨识

计算结果Z向频率与试验结果接近，误差在5%左右说明计算方法是比较合理的。有一定误差，是由于惯性参数和等效质量均是通过软件获取，与实物有一定偏差，另外实车中拉杆悬置安装在副车架上，副车架再与车身和其他部件连接，有一定的刚度和阻尼，而计算模型忽略了这个因素。

拉杆悬置的解耦计算结果，主要考察其Z向频率，识别其是否达到避频目标要求。而解耦率反映的是以拉杆悬置为系统的各方向振型的耦合程度，由于各频率间隔较大，一定程度的耦合并不一定会引起整车噪声问题，故本案例中解耦率不做重点考察。改进方案计算结果Z方向频率为76Hz，对比原状态99Hz降低明显，达到20Hz的避频经验值，故认为改进方案能够满足避频的要求。

2.3 实验验证

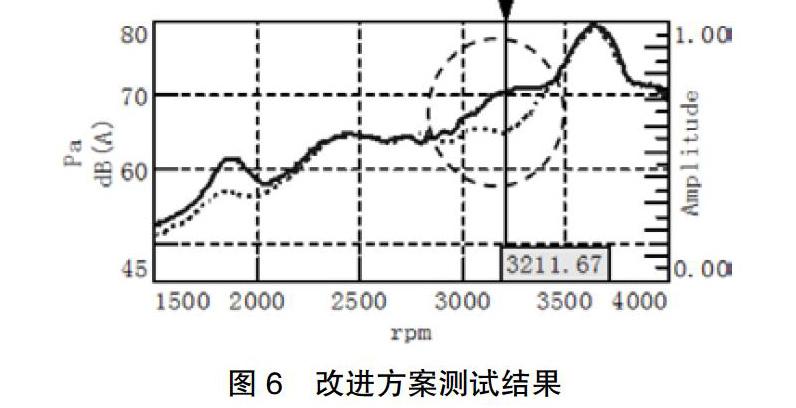
供应商制作样件装车，通过锤击实验，拉杆悬置Z向频率为79Hz，与计算结果非常接近。通过车内噪声测试、整车主观评价发现3200RPM左右的加速轰鸣消失，原加速轰鸣问题附近的声压级曲線有最大5dB（A）左右的降低，改善效果明显，测试结果图6所示（实线为原方案，点化线为改善方案）：

3 总结

（1）本文通过解耦理论在计算拉杆悬置刚体模态上的应用，成功的解决了加速轰鸣问题。

（2）扩展来看，该方法也能够量化评估拉杆悬置橡胶衬套各向刚度、弹性中心位置、安装角度的改变带来的刚体模态的变化，具有较强的工程应用意义。

参考文献：

[1]余志生，李克强等.汽车工程手册：基础篇[M].北京：人民交通出版社，2001（405）.

[2]庞剑，谌刚等.汽车噪声与振动-理论与应用[M].北京：北京理工大学出版社，2006：7-10.

[3]潘威，史晓宁等.汽车加速车内轰鸣声控制研究[J].客车技术与研究，2020（02）：57-59.

[4]武守涛，蒋小余等.基于拉杆式悬置刚体模态控制的加速车内轰鸣声优化-2016中国汽车工程学会论文集[C].2016：1072-1073.

[5]赵静，周鋐等.轿车乘坐室轰鸣声的分析与控制研究[J].汽车技术，2009（10）：16-20.

[6]吕振华，范让林.动力总成-悬置系统振动解耦设计方法[J].机械工程学报，2005（04）：49-53.

[7]周昌水，邓兆祥等.动力总成悬置系统建模与解耦优化[J].客车技术与研究，2007（03）：4-5.

[8]方锡邦，陈树勇等.轿车动力总成悬置系统隔振性能的仿真研究[J].合肥工业大学学报，2003（04）：236-239.

[9]唐政飞.于刚体动力学的动力总成悬置系统的建模分析[D].华中科技大学，2015（05）.

[10]时培成.汽车动力总成悬置系统隔振分析与优化研究[D].合肥工业大学，2012（12）.

[11]付江华，周鹏等.某乘用车动力总成悬置的NVH性能分析与优化[J].机械设计与制造，2018（06）：226-232.

[12]李响，周鋐.动力吸振器在轿车低频轰鸣声控制中的应用[J].设计与开发，2015（01）：9-11.

[13]时培成，李文江等.基于振动传递率和能量解耦的悬置系统优化[J].先进制造工艺技术，2009（02）：17-18.