基于模糊PID两轮拖拉机控制系统抗干扰分析

张轩 李志伟 郑德聪

摘要：利用陀螺力矩效应建立了两轮自平衡拖拉机动力学模型，针对拖拉机机体控制系统，提出了一种基于模糊自适应理论的侧倾角控制器/旋进角控制器PID控制算法。在Matlab/Simulink环境下，分别搭建了拖拉机侧倾角控制系统、陀螺旋进角控制系统仿真模型，并加入随机干扰进行仿真研究。仿真结果表明，应用在两轮自平衡拖拉机控制系统的模糊自适应PID控制系统在加外干扰后消除响应振荡现象、加快响应速度、提高响应精度方面明显优于传统PID控制系统。

关键词：两轮自平衡拖拉机;力矩陀螺;BLDCM;模糊自适应PID;Simulink仿真

拖拉机作为农业生产的一种多用途重要牵引动力装置，与各种牵引式、悬挂式作业机具连接后可对作物进行各种加工[1]，而作物狭窄的植株行距限制了四轮拖拉机的应用，本研究提出可应用于狭窄田间的两轮拖拉机。两轮车的力学模型为非线性欠驱动非完整约束系统[2]，在车速低于5 km/h情况下难以保持车身平衡[3]，而田间土壤的复杂性加剧了两轮拖拉机的不平衡，相关研究针对两轮车平衡问题提出了方向转向、重量平衡、力矩陀螺等控制方案[2-7]，而力矩陀螺以其具备控制精准、侧倾调控范围较大的特点[5]成为研究重点。

针对两轮自平衡拖拉机侧倾角度动态响应问题，采用部分反馈线性化方法将拖拉机机体非线性系统转化为线性系统，为拖拉机控制系统设计出基于模糊自适应理论的侧倾角控制器、旋进角控制器，使用Matlab/Simulink对两控制器动态性能进行仿真，同时在模型中加入高斯白噪声，表明在外界干扰不确定的情況下，自适应模糊PID控制系统能有效地保证两轮自平衡拖拉机的稳态精度。

1 两轮自平衡拖拉机模型

在两轮间安装一组高速自转的力矩陀螺，并通过两陀螺间的驱动电机控制陀螺自转轴线的朝向，产生矫正拖拉机侧倾角的控制力矩（图1）。

1.1 陀螺力矩效应原理

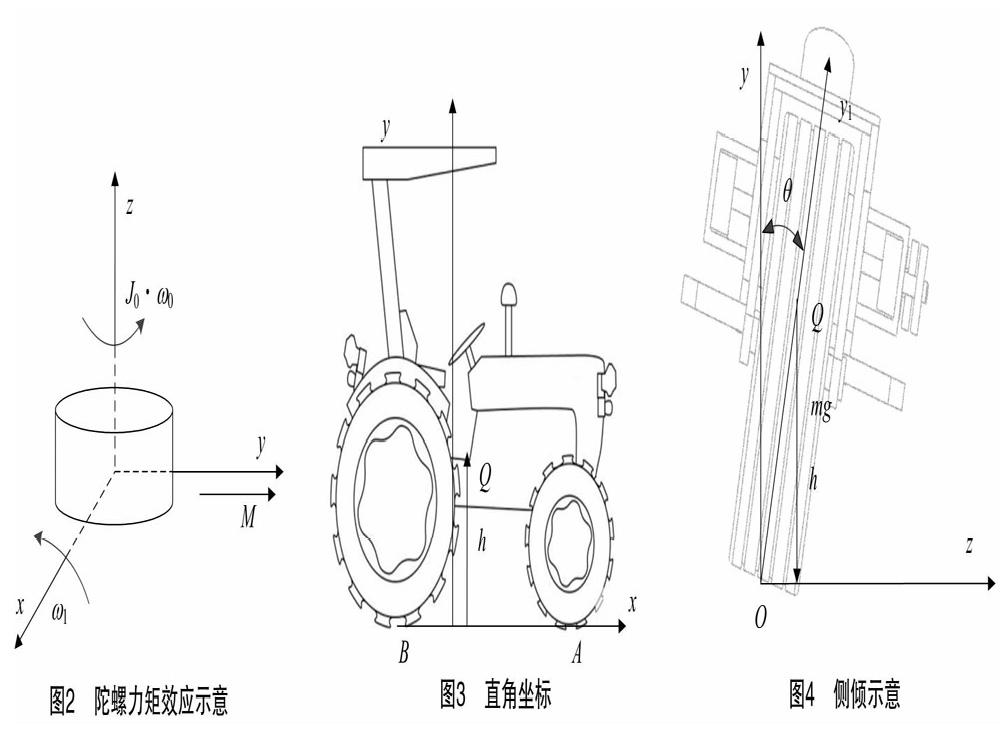
从图2可以看出，转动惯量为J0的陀螺以ω0围绕z轴高速旋转，当陀螺本身围绕x轴以ω1旋转时，陀螺将产生一个沿y轴方向的力矩[8]：

当陀螺以定值ω0高速自转，通过电机控制陀螺的旋进方向，产生平衡力矩。

1.2 两轮自平衡拖拉机动力学建模

建立直角坐标系见图3，在两轮自平衡拖拉机未发生侧倾时，以A、B点连线作为x轴，以通过B点的铅垂线作为y轴，x轴与y轴相交于B点，通过右手法则建立z轴。当两轮拖拉机发生侧倾时截取yOz平面（图4），由角动量守恒原理可得，以x轴为旋转主轴的方程为：

1.3 陀螺力矩自平衡原理

由公式（2）可知，需引入控制力矩u使车体侧倾角恢复为0°：

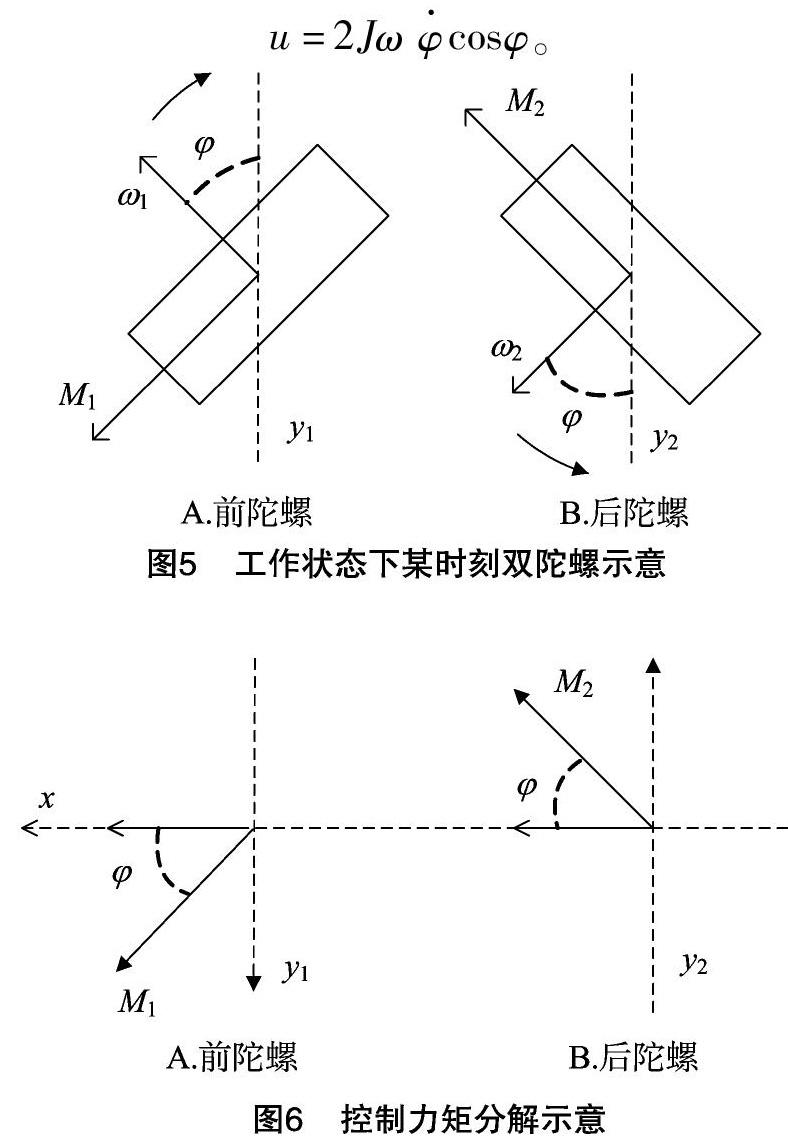
以图4为例，当车体发生右倾时，mghsinθ方向为x轴负向，控制力矩需为x轴正向。截取力矩陀螺所在的平面xOy，ω1、ω2为前陀螺、后陀螺的自转角速度，以陀螺自转轴与y1、y2的夹角模φ为陀螺旋进角，φ·为旋进角速率（图5、图6）。为使两陀螺x方向的力矩叠加，y方向的力矩抵消，需保证两陀螺转动惯量、自转角速率、旋进角速率均相等，自转方向及旋进方向均相反，结合公式（1）得出，陀螺控制力矩：

2 控制方案设计

由此可见，两轮自平衡拖拉机为非线性二阶系统。

2.1 拖拉机机体侧倾角控制方案设计

θ为拖拉机机体侧倾角，θ·为拖拉机机体侧倾角角速率，可由倾角传感器实时测得（图7）。采用反馈线性化控制方法[4]，在陀螺控制力矩中引入 -mghsinθ，u1为控制力矩中线性部分。

式中：K为角速度反馈系数。

2.2 陀螺旋进角控制方案设计

φ为力矩陀螺的旋进角，可由倾角传感器实时测得。联立公式（4）、公式（6）、公式（8）可得陀螺实时应达到的旋进角角速率φ·ref。以φ·ref为陀螺旋进角参考输入量、φ·为最终响应值建立旋进角控制系统（图8）。因永磁无刷直流电机（BLDCM）具备体积小、结构简单、成本低廉、效率高、控制效果良好、控制策略方便等优点，选用BLDCM作为力矩陀螺旋进角调速电机。

3 模糊自适应PID控制器的设计

拖拉机工作环境恶劣、工况复杂，还需匹配不同的农用机具进行作业，往往存在作业时载荷不均匀、载荷扰动、强振动冲击的问题，在控制领域中体现为不同程度地非线性、时变性、模型不确定性，而模糊PID控制方式既具有PID控制器快速响应、稳定性高的特点，又具有模糊控制方式降低超调量、抗扰动能力强的特点，因此将模糊PID控制方式引入到拖拉机机体侧倾角控制系统及力矩陀螺旋进角控制系统中。

3.1 模糊集及论域定义

模糊控制器以误差e和误差变化率ec作为输入，误差变化率为误差对时间的一阶导数[9]，经过模糊控制规则表推理，使用“Mamdani”解模糊法，以ΔKP、ΔKI、ΔKD作为输出量，输出信号实时调整PID控制器各参数，实现系统自适应调整功能，其控制原理见图9。

模糊集定义为：{PB正大，PM正中，PS正小，ZO零，NS负小，NM负中，NB负大}。对于侧倾角控制器，输入信号为拖拉机的实际侧倾角和理论输入量，输入域e、ec为[-6，6]，输出域ΔKP、ΔKI、ΔKD为[-300，300]、[-10，10]、[-10，10]。对于旋进角控制器，输入信号为电机的实际旋进角和理论输入量，输入e为[-6，6]，输入ec为[-1，1]，输出域ΔKP为[-6，6]，ΔKI为[-0.3，0.3]，ΔKD为[-0.03，0.03]。对于各个输入及输出域模糊集，NB及PB均选取gaussmf型隶属度函数，其余各语言值均选取trimf型隶属度函数（图10）。

3.2 模糊PID控制器模糊规则表

对于模糊PID控制器，当e较大时，需取较大的KP，以加快系统的响应速度，同时适当调整KD，使系统具有一定的响应性，消除静态误差;当e较小时，应适当调整KP、KD，加快系统动作，减少调节时间[10]。由此可得输出变量KP、KI、KD的模糊控制规则（表1、表2）。

3.3 仿真模型

利用Matlab/Simulink将模糊自适应PID控制器加入拖拉机机体侧倾角控制系统及力矩陀螺旋进角控制系统，仿真模型见图11、图12、图13。

其中，力矩陀螺旋进角控制系统包含电流内环、转速外环，转速外环使用模糊PID控制。仿真中，车体J=100 kg/m2，BLDCM参数设定为：Rs=0.5 Ω，Ls=0.01 H，转子磁链φf=0.119 4 Wb，转动惯量J=0.002 7 kg/m2，摩擦系数B=0，极对数 np=1，初始转速ωi=0，初始转子角度θ=0°。

4 仿真及抗干扰分析

在Matlab/Simulink中对拖拉机机体侧倾角控制系统仿真，采样时间为1×10-4 s，仿真时间为 2 s，设置初始侧倾角度为15°，初始输入角度为0°（平衡位置）。在Matlab/Simulink中对力矩陀螺旋进角控制系统仿真，采样时间为1×10-4 s，仿真时间为0.4 s。设置初始输入转速1 000 r/min，初始负载0.3 N，在0.2 s处将输入转速变更为 2 000 r/min。设置初始输入转速1 000 r/min，初始负载1 N，在0.1 s将负载减至0.3 N，在0.3 s将负载加至2 N。

对拖拉机体控制系统输入端加入零均值均方差为2的高斯白噪声作为外干扰，对力矩陀螺旋进角控制系统输入端加入零均值均方差为3的高斯白噪声作为外干扰。

从图14、表3可以看出，对于拖拉机机体侧倾角，利用模糊PID控制能减小超调量。

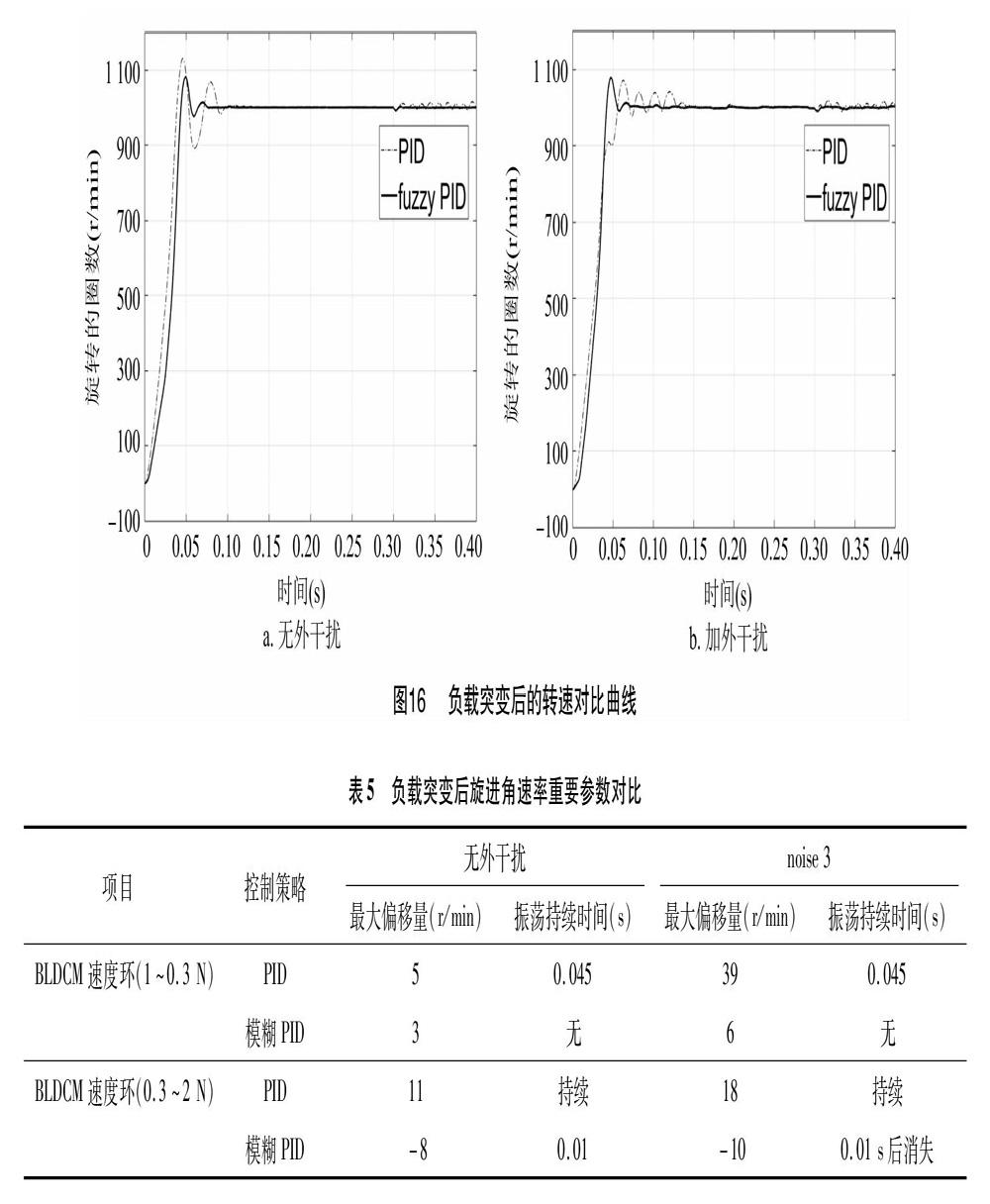
从图15、表4可以看出，对于力矩陀螺旋进角角速率，从0 r/min到1 000 r/min过程中，在外干扰作用下，模糊PID超调量较小，调节时间缩短了24%，且相比于PID无振荡出现。从1 000 r/min到 2 000 r/min 过程中：在外干扰作用下，模糊PID超调量较小，上升时间缩短了81%，调节时间缩短了28.5%，且相比于PID无振荡出现。因此模糊PID较PID更为准确、快速、稳态精度高。

从图16、表5可以看出，对于力矩陀螺旋进角角速率，在外干扰作用及0.1 s及0.3 s发生负载突变的情况下，模糊PID最大偏移量绝对值较PID少了27%，且相比于PID基本消除了振荡现象。

综上所述，对于拖拉机机体侧倾角控制系统、力矩陀螺旋进角控制系统，模糊PID控制器相比于PID控制器具有更高的准确性、快速性及稳态精度。

5 结论

本研究设计了一种基于反馈线性化方法的两轮自平衡拖拉机控制方法，针对所设计的响应过程，为拖拉机机体侧倾角控制系统、力矩陀螺旋进角控制系统设计了模糊PID控制器，并进行Matlab/Simulink模型仿真，仿真结果表明，在存在外界干扰的情况下，所设计的模糊PID控制器能有效地保证拖拉机控制系统的稳态精度，提高控制系统的鲁棒性，为研究两轮自平衡拖拉机控制系统提供了方向。

参考文献：

[1]高辉松，王珊珊，朱思洪. 电动拖拉机驱动力与传动效率特性试验[J]. 农业机械学报，2008，39（10）：40-43，58.

[2]黄用华. 前轮驱动自行车机器人建模与几种平衡运动控制研究[D]. 北京：北京邮电大学，2011.

[3]strm，Karl J，Klein R E，et al. Bicycle dynamics and control：adapted bicycles for education and research[J]. IEEE Control Systems Magazine，2005，25（4）：26-47.

[4]熊宇聰，张 猛. 基于反馈线性化的两轮自平衡汽车侧倾动态响应控制[J]. 制造业自动化，2018（7）：138-143，153.

[5]Tamayo-León S，Pulido-Guerrero S，Coral-Enriquez H. Self-stabilization of a riderless bicycle with a control moment gyroscope via model-based active disturbance rejection control[C]//2017 IEEE 3rd colombian conference on automatic control （CCAC）. IEEE，2017：1-6.

[6]李 勇，耿建平，林群煦，等. 基于双飞轮陀螺效应的两轮自平衡机器人的研制[J]. 机电产品开发与创新，2015，28（6）：14-16，28.

[7]李 静. 前轮驱动自行车机器人建模与自适应控制策略研究[D]. 北京：北京邮电大学，2017.

[8]周龙加. 一种基于陀螺进动效应的稳定装置研制[J]. 机电信息，2016（24）：100-101.

[9]刘慧博，王 静，吴彦合. 无刷直流电机模糊自适应PID控制研究与仿真[J]. 控制工程，2014，21（4）：583-587.

[10]王 葳，张永科，刘鹏鹏，等. 无刷直流电机模糊PID控制系统研究与仿真[J]. 计算机仿真，2012，29（4）：196-199，254.姚永亮，沈 鹏，魏光程，等. 基于Creo的仿生马铃薯培土器设计及仿真分析[J]. 江苏农业科学，2020，48（12）：222-225.