随机森林算法在测井岩性分类中的应用
2020-07-20康乾坤路来君
康乾坤,路来君
吉林大学 地球科学学院,长春 130061
0 引言
岩性分类识别是地质工作中重要的一部分,通过对岩性的识别分类,可以直观地表达出岩石地球物理属性在纵深维度上的变化特征和规律,揭示出油藏、气藏和矿藏等的潜在分布特性[1]。对于岩性信息的获取多依靠实地岩芯取样、交会图[2]和聚类分析[3]等传统方法和数理统计手段,随后发展为神经网络[4-9]、支持向量机[10]等机器学习方法。传统方法中实地岩芯取样和岩芯编录所获取的资料质量较高,是宝贵的地质基础资料,但是存在人力成本和时间成本较高的不足。随着测井技术的不断完善,物探测井信息的丰富度也越来越高,在庞杂的物探测井数据中如何快速有效地获取储层岩性信息逐渐成为提升地质工作效率的一个重要问题。
机器学习算法用以解决地质问题,为提升地质工作的效率提供了新的思路和方法。前人已做大量的相关工作。岩性识别中的机器学习方法由最初基于无监督的聚类分析法[3]、无监督的自组织竞争神经网络[6]等,迅速发展到后续基于有监督的BP神经网络[7]、卷积神经网络[8]和基于遗传算法的BP神经网络[9]等,准确率不断地提升,识别效果也越来越明显。目前这些方法也存在一些问题和不足,神经网络方法容易存在过拟合、收敛速度较慢等问题[8];支持向量机则较大程度上依赖于核函数的选取和惩罚系数的选择[10];无监督学习的方法存在分类类别难以控制以及需要足够大的样本群来保证性能等不足[6]。因此有必要探索出更稳健、更适用的机器学习方法来处理地质应用中岩性自动识别分类的问题。
随机森林算法是一种由大量随机决策树所构成的集成机器学习算法。算法保留了决策树分类的优势,同时拥有更好的容错性[11-13],广泛应用于数据分析、数据挖掘领域,具有较好的处理高维数据的能力[14-15]。综上所述,本文选择随机森林算法应用于测井岩性的分类识别。将物探测井数据作为随机森林算法的输入变量,对岩性进行有监督的分类预测识别,依据结果评价算法的有效性,对不同的测井参数变量在岩性分类中的作用予以分析。
1 研究区概况及数据
研究区位于松辽盆地大庆长垣南端某铀矿矿区,松辽盆地是中国东北地区中部的一个大型中新生代陆相沉积盆地[16]。大庆长垣位于松辽盆地北部一级构造单元中的中央坳陷区内,是盆地内最大的背斜构造[17]。研究区位于大庆长垣地块的最南端(图1)。
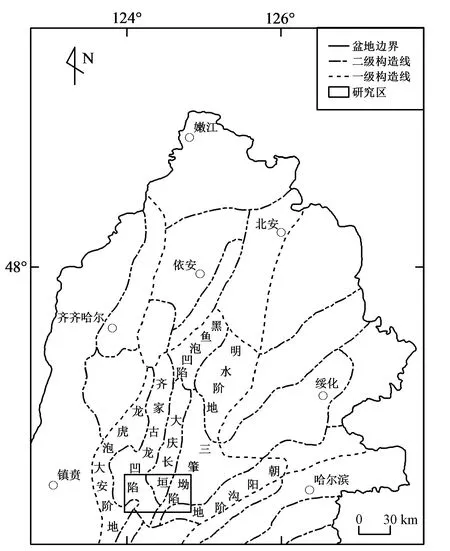
图1 研究区构造位置图[18]Fig.1 Tectonic location map of study area
研究区内铀矿钻孔数据每孔共计有8条测井曲线,分别对应自然伽马、放射性、自然电位、三侧向电阻率、视电阻率、井径、密度和声波时差共计8项物探测井参数。测井数据属性信息和分辨率详见表1,以0.125 m为采样间隔,覆盖范围为地表至地下450余米,测井曲线的丰富程度高,岩芯保存完好。岩性数据均为准确岩芯定名资料,由天津地质调查局野外地质钻孔编录完成。目前具有完整岩性信息的钻孔共计22口井,单井内依据岩性划分对应测井数据,平均测井样本点2 800余个,均具有明确对应的定名岩性信息。为本文研究工作提供了有力的支持。测井岩性柱状图详见图2。
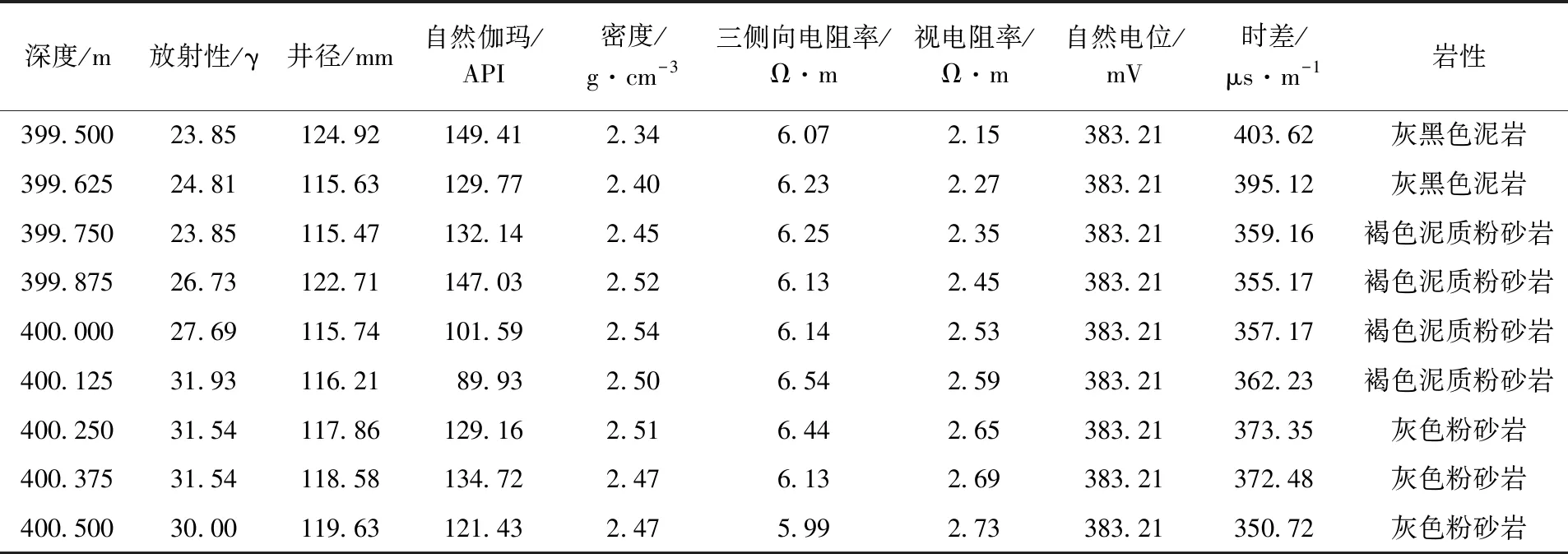
表1 研究区钻孔测井数据示例

图2 研究区某钻孔测井岩性柱状图Fig.2 Logging data of a well in study area
2 不同岩性的测井响应特征
研究区内的主要地层自上而下划分依次为明水组-四方台组-嫩江组,分布深度由地表至地下450 m的范围内,纵深方向上未见有断层,地层分布较为均匀,起伏变化较小[19]。研究区内的主要岩性分布为贴近地表较薄的黏土层、厚砂岩层、泥岩层以及部分砾岩岩层。各个岩性类别由于其理化性质的差异,对测井曲线有着不同的响应特征,有一定的规律可循。不同岩性的测井响应特征规律主要为:
(1)在自然伽马测井中,由于粒级的不断细化,孔隙度不断减小,诸如K、Th、U等放射性元素逐渐聚集于致密岩层中,导致致密岩层的放射性数值普遍偏高[20],自然伽马测井数值大小表现为:泥岩>砂岩>黏土>砾岩。
(2)在自然电位测井中,自然电位曲线因受岩层中泥质含量的影响,浸透性高的地层自然电位参数表现为较大的负异常,渗透性低的岩层自然电位表现为较小的负异常[21]。粉砂岩、细砂岩以及泥岩等渗透性较低的岩性类别自然电位值较小,中砂岩、粗砂岩和砾岩则相对较高(图3)。
(3)密度的变化幅度较小,主要受岩层内夹杂物质的含量以及岩石孔隙度的影响而出现波动,黏土(1.89 g/cm3)<砂岩(2.23 g/cm3)<泥岩(2.26 g/cm3)<砾岩(2.37 g/cm3)。砂岩层孔隙度略高于泥岩层,密度略小于泥岩层。砾岩岩石密度较大,但孔隙度亦较大,密度平均值较高。
(4)电阻率曲线随着岩石粒度的变化而变化,随着岩石粒度逐渐变小,从砾岩-砂岩-泥岩的粒度变化对应的电阻率幅值呈由大到小的总体变化规律(20~30 Ω·m)→(5~10 Ω·m)[20]。

图3 不同岩性的自然电位箱线图Fig.3 Boxplot of spontaneous potential with different lithology
(5)井径曲线同岩层的致密程度有较大的关系,随着测井仪器中钻头的下探,井壁物质的致密程度直接决定井径的大小。黏土、细砂岩、中砂岩、粗砂岩和砾岩的井径基本保持在125~127 mm,在粉砂岩和泥岩层中井径则扩大至136~140 mm。
各岩性类别测井响应特征的差异在测井数据中表现为测井曲线幅值范围的不同。以研究区某一钻孔为例,不同测井曲线的数值差异详见表2,不同岩性类别在自然电位测井响应数值范围的箱线图见图3。
不同岩性类别在同一测井参数的数值响应规律存在明显的差异,最大最小值和均值的不同代表了岩性类别间的总体差异,中位数和均值的差异体现了数据聚集程度的不同。各个岩性类别测井数据统计量所表现出的差异亦从侧面验证了岩性类别基于测井数据的可分性。综上所述,岩性类别的测井响应规律为岩性类别的划分提供了理论基础的支持,特别是在基于数值型测井数据的岩性类别划分工作中,错综复杂的响应特征组合及其对应的岩性所属类别是机器学习方法所要掌握的核心知识。
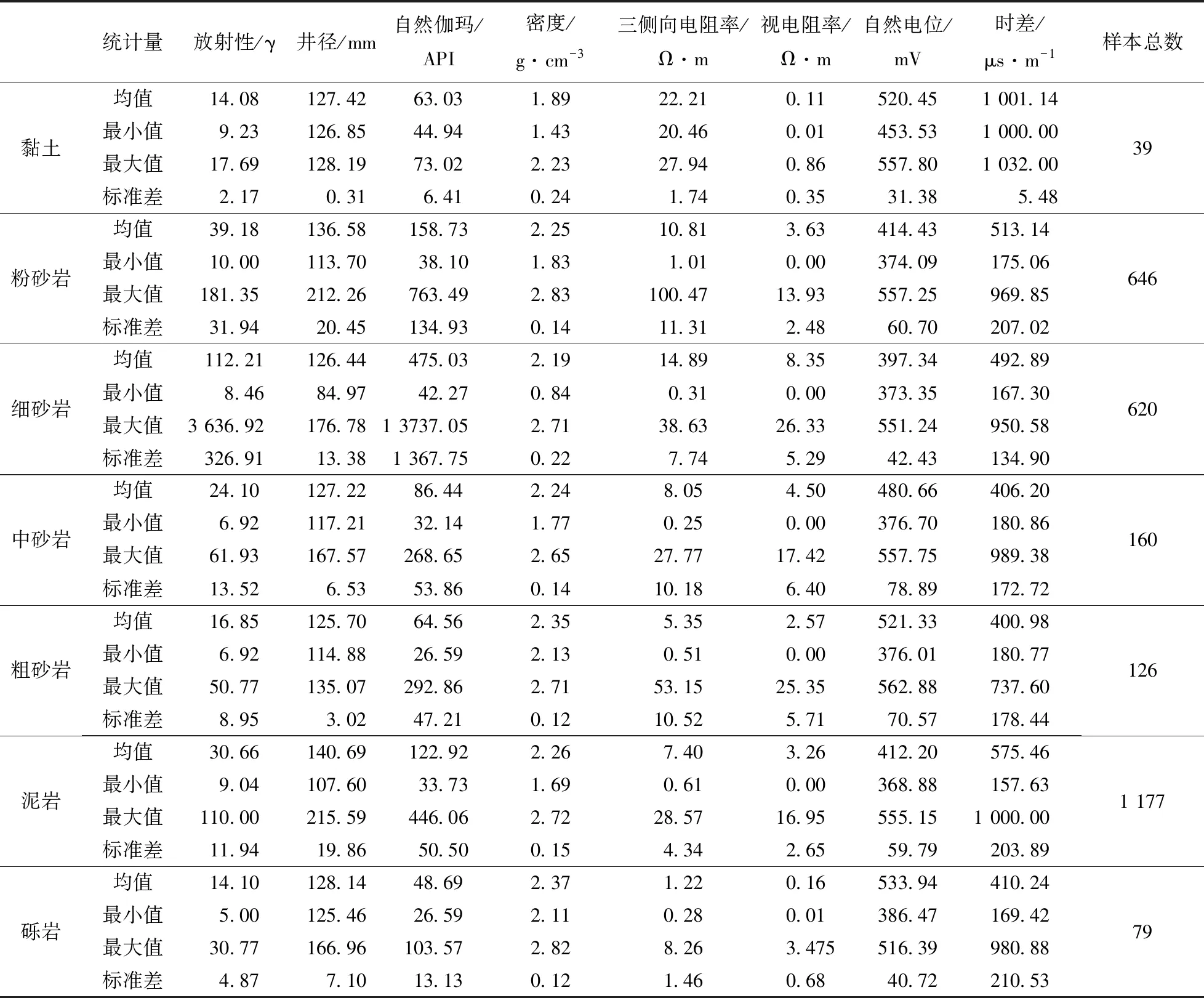
表2 不同岩性类别的测井数据统计
3 随机森林算法的原理
随机森林算法是由Breiman于2001年提出的一种集成多棵决策树的有监督学习算法,基于数据处理结果的类型,随机森林可以完成分类和回归两种应用,属于机器学习方法中的一种[13]。随机森林算法的核心思想是基于众多随机决策树判别结果的最优分类和回归,解释输入变量X1,X2,X3,…Xn对解释变量Y的作用。决策树是随机森林的核心所在,依据条件熵和信息增益保证决策树的最优生成。其基本原理为:
(1)通过Bagging的方法从样本数为N的数据集D中,随机且有放回地选取不同变量数、不同样本数的参数组合,用以形成众多的随机决策树并决定每棵树的分类节点[12]。如此形成的决策树对于大数据量的样本具有较好的容错性。
(2)计算数据集D的信息熵,以及各个变量Xi同D之间的条件熵。信息熵可称之为数据集的平均不确定性。条件熵H(D|Xi)是在数据集D发生的前提下,Xi变量所带来的熵值变化。数据集D的信息熵为H(D):
(1)
式中:Di为数据集D中第i个数据出现的概率。
数据集D同变量之间的联合熵H(D,Xi)为:
(2)
数据集D同变量之间的条件熵为:
H(D|Xi)=H(D,Xi)-H(Xi)
(3)
(3)计算每一个变量Xi相对于数据集D的信息增益g(D,Xi),用以度量特征Xi对数据集D的不确定性的减小程度。不确定性的减小程度即为D发生概率的增加。信息增益的计算公式如下:
g(D,Xi)=H(D)-H(D|Xi)
(4)
(4)以信息熵为度量生成熵值下降最快的树,同时选择信息增益率和Gini系数最大的变量作为决策树分裂节点的变量。到叶子节点处熵值降为0,至此,每个叶节点由于其熵值最小原则,均属于同一类别。Gini系数的计算公式如下:
(5)
(5)基于随机选取的样本变量参数组合便可生成大量可并行处理的随机决策树,这些随机决策树共同组成了随机决策森林。每一棵决策树会根据待分类的数据给出一个基于该分类树的分类结果,并最终汇总全部森林里重复度最高的决策树的结果为随机决策森林的分类结果。
随机森林算法的另一大优势在于参与该算法可以给出关于分类变量重要性的度量[14]。通过计算变量对数据集的信息增益率来判断变量的贡献值,变量的信息增益率越大,表明该变量对熵值减少的能力越强,该变量使数据由不确定性变为确定性的能力便越强,可应用于样本的变量筛选。
4 实验设计及结果分析
以不同岩性的测井响应特征为理论依据,8条物探测井曲线为输入变量,利用随机森林算法对研究区的钻孔测井岩性进行分类识别,将研究区内的数据进行统计分析,参照岩性类别划分的规范和标准,给出研究区7种岩性类别,初次实验采用单钻孔全部数据进行算法处理,训练样本同预测样本比例为7∶3,随机取样以保证模型的广泛性(表3)。由于随机森林算法需要对初始参数进行合适的选取,不同的初始参数会导致不同的分类结果[15]。故而初始参数的设置采用初始参数值域最小值为初始参数,通过逐次递增迭代循环的方法筛选出最优的参数组合,即决策树的数目和决策树所采用的节点个数。
为了有效地了解不同变量对分类结果的作用或影响,利用训练数据进行随机森林算法的袋外误差验证和变量重要性的度量。算法的袋外误差在于随机选取训练样本进行准确率验证,保证训练的合理性。预测数据则用以对随机森林算法进行精度检验。采用混淆矩阵对随机森林算法的岩性分类结果进行精度评价,给出分类结果的总体精度以及各个岩性类别的生产者精度和用户精度。在相同的训练条件下,引入支持向量机方法,对两种方法的预测结果进行对比分析。
表3 岩性划分类别及样本数据分布
Table 3 Classification of lithology and distribution of sample data
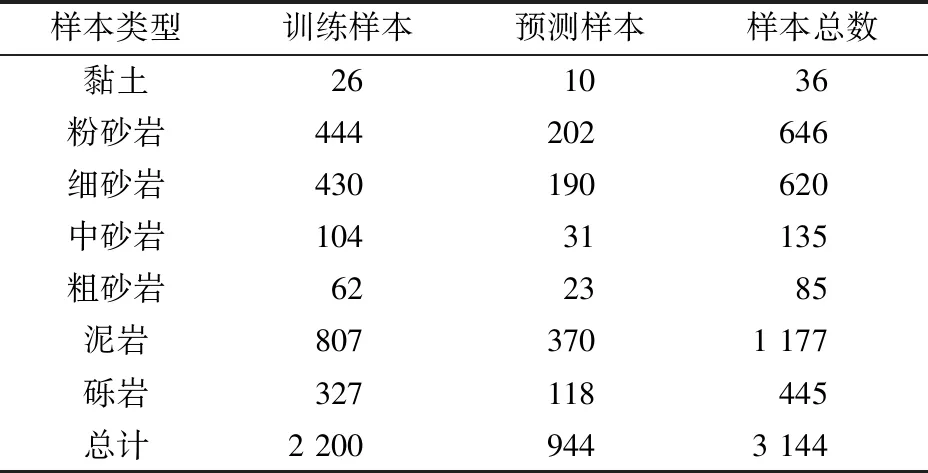
样本类型训练样本预测样本样本总数黏土261036粉砂岩444202646细砂岩430190620中砂岩10431135粗砂岩622385泥岩8073701 177砾岩327118445总计2 2009443 144
本次实验利用R语言完成,R的版本为(R.3.6.0)。初始决策树棵数设置为100棵,决策树所采用的节点数预设为变量数的算术平方根,即为1个。实验表明在决策树为567棵时,决策树节点为3个时,随机森林算法的分类效果最优,袋外误差的验证准确率为88.05%(表4)。支持向量机方法采用径向基函数为核函数,gamma值依据支持向量机理论设置为变量个数的导数0.125,cost惩罚因子设置默认值为1。
依据训练后的模型,对全钻孔30%随机取样的预测样本进行分类识别,随机森林算法的分类准确率为88.67%,同时支持向量机方法的分类准确率为73.2%(表5)。
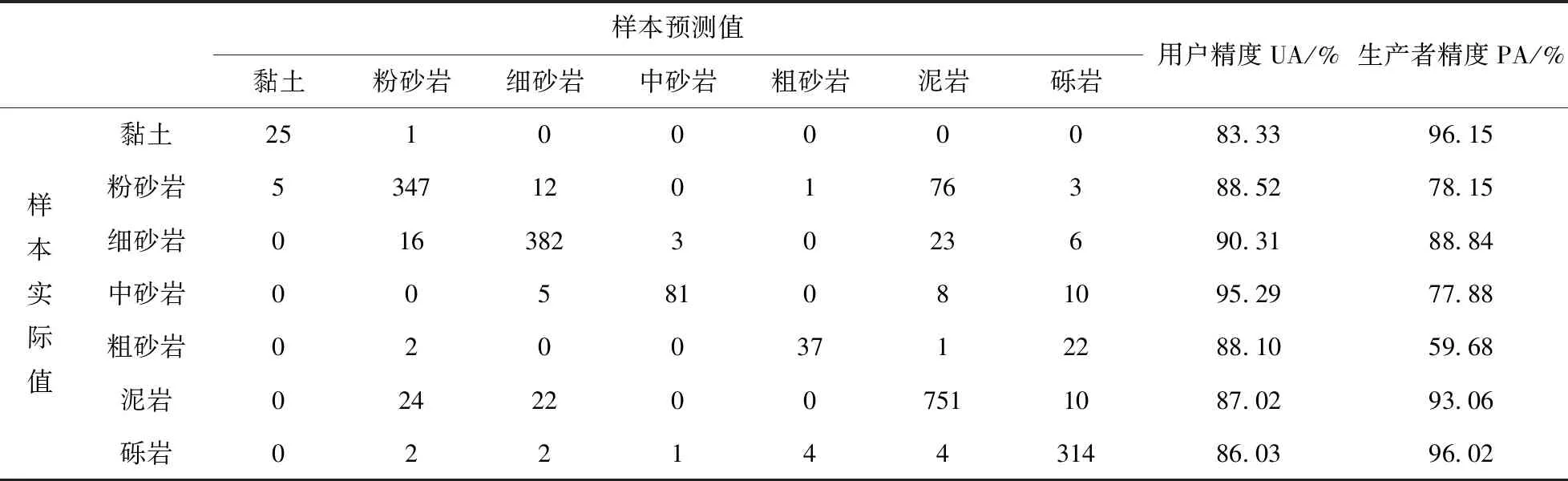
表4 随机森林算法训练样本预测结果
表5 不同算法预测样本分类结果
Table 5 Classification results of prediction samples with different algorithms

岩性类别随机森林算法支持向量机方法用户精度/%生产者精度/%用户精度/%生产者精度/%黏土80.00100.00100.0088.89粉砂岩78.7188.8354.3665.84细砂岩90.0090.0076.4180.11中砂岩64.5290.9131.8293.33粗砂岩73.9189.4747.0066.67泥岩93.2489.1582.7771.99砾岩99.1584.1795.9773.01总体精度88.6773.20
对比表5,随机森林算法在总体预测分类准确度和单个岩性的分类准确度方面均要优于支持向量机方法,其中两种算法对于中砂岩和粗砂岩的识别准确率均低于其他岩性,支持向量机方法对于粉砂岩的准确率也较低。出现较高分类误差的主要原因是由于不同类型的砂岩之间过渡不明显,相较于不同岩性之间的区分度较低。通过对岩芯编录数据的分析,不同类型的砂岩会以夹层的形式出现,导致分类误差的升高。岩芯编录分析的数据较为精细,而实验设计相较之原始数据有所精简,根据粒级的不同将砂岩划分为粉砂岩、细砂岩、中砂岩和粗砂岩4类,这其中出现诸如含砾粗砂岩、含砾中砂岩和泥质粉砂岩等互层岩性的存在,实验设计时将其均归类为主要岩性,即含砾粗砂岩归类为粗砂岩,泥质粉砂岩归类为粉砂岩。由于其含砾和含泥质等特性的存在,在测井参数的数值中体现为接近于砾岩、泥岩等现象,致使区分度的降低和分类误差的升高。在单个岩性识别准确率和总体识别准确率中,随机森林算法均明显优于支持向量机算法,表明基于众多决策树投票机制的随机森林算法在岩性分类识别应用中优于支持向量机方法。
根据随机森林算法变量重要性的分析,得出各个测井变量的平均下降准确率和平均下降Gini系数(表6),两者均表达该变量被替换时准确率下降程度的度量,数值越大,该变量的重要性程度越高[14]。在岩性分类的应用中,三测向电阻率、自然电位和视电阻率是重要性较高的变量,自然伽马和井径也可作为较好的分类变量,重要性较低的变量为时差和密度。究其原因,在于该变量在不同岩性类别间的区分度不高,以密度测井为例,各个岩性类别的密度均值、标准差和中位值较为接近(图4)。在复杂岩层和过渡岩层中难以发挥区分的作用。
表6 岩性分类变量重要性度量
Table 6 Measurement of importance of lithology classification variables

平均下降准确率/%平均下降Gini系数三侧向电阻率100.112 23363.316 5井径98.087 27199.219 7自然电位88.752 04266.790 8时差74.915 43139.173 2视电阻率72.836 54255.339 2密度62.600 44111.792 6自然伽马61.905 86193.825 5放射性58.872 13144.196 6
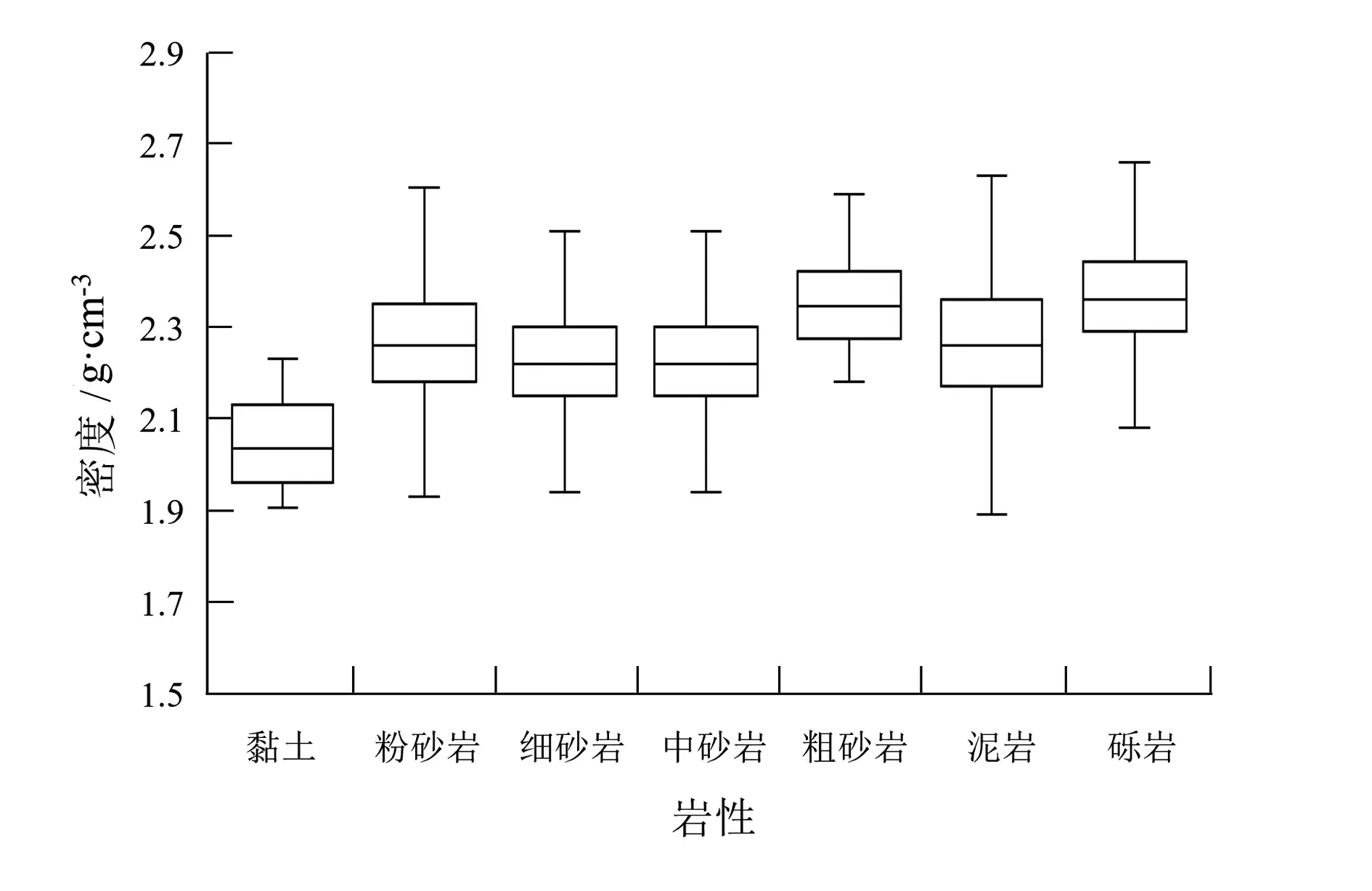
图4 不同岩性的密度箱线图Fig.4 Boxplot of density with different lithologies
5 结论
(1)利用随机森林算法进行岩性自动分类识别,预测准确率为88.67%,效果明显优于支持向量机方法。
(2)中砂岩和粗砂岩常伴有互层形式出现,是随机森林算法岩性识别的难点。
(3)通过随机森林算法的平均下降准确率得出,自然电位和电阻率是岩性分类应用中重要性较高的测井变量。
