A new variable step-size LMS method and its applicationin DOA estimation of OFDMA signals

Zhao Yan Lin Li Dong Wen Wang Hao Wu Zhentao Wang Xiaojun Chen Xiaoshu

(1The PLA’s 61212 Army, Beijing 100000, China)(2School of Optics and Photonics, Beijing Institute of Technology, Beijing 100081, China)(3National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract：To meet the requirements of quick positioning of mobile terminals from base stations (BSs) or third-party devices, as well as to improve the convergence speed and reduce the steady state maladjustment of the least mean square (LMS) method, a new logarithmic-sigmoid variable step-size LMS (LG-SVSLMS) was proposed and applied to estimate the direction of arrival (DOA) of orthogonal frequency division multiple access (OFDMA) signals. Based on the proposed LG-SVSLMS, a non-blind DOA estimation system for OFDMA signals was constructed. The proposed LG-SVSLMS adopts a new multi-parameter step-size update function which combines the sigmoid function and the logarithmic function. It controls the adjustment magnitude of step-size during the initial and steady state phases of the LMS method to achieve both a high convergence speed and low steady state maladjustment. Finally, simulation was conducted to verify the performance of the LG-SVSLMS. The simulation results show that the non-blind DOA estimation system based on the LG-SVSLMS can accurately estimate the DOA of the target signal in the scenario where interference signals from multi-source and multi-path fading signals arrive at the third-party devices asynchronously with the target signal, and the estimation deviation is within ±3°. The non-blind DOA estimation for OFDMA signals with the proposed LG-SVSLMS is of great significance for the instant positioning technology of mobile terminals based on the adaptive antenna array.

Key words：direction of arrival; variable step-size least mean square; orthogonal frequency division multiple access; third-party devices

With the rapid development of communication technology, the output of global mobile terminals has increased exponentially. The mobile terminal positioning technique is widely utilized in the signal propagation of hotspot areas, location tracking, emergency rescue, emergency communication and other fields. Currently, the location information of terminals is provided mainly by satellite and cellular network positioning. Satellite positioning mainly includes the global positioning system (GPS)[1]and the Chinese Beidou navigation satellite system (BDS)[2]. Satellite positioning can accurately locate within a visible distance in the open environment, but it is greatly interfered by multi-path fading signals in large and medium-sized cities. Cellular network positioning enables accurate location over a wider range due to its wide and deep coverage.

In recent years, adaptive antenna arrays have been gradually applied to various mobile communication systems. Thus，wireless positioning based on adaptive antenna arrays has received extensive attention. Compared with satellite positioning, wireless positioning only needs relevant equipment to be provided to the base stations (BSs), instead of optimizing and improving numerous terminal devices. At present, the direction of arrival (DOA) estimation methods based on adaptive antenna array can be divided into blind DOA estimation and non-blind DOA estimation. Blind DOA estimation methods mainly include Capon minimum variance[3], multiple signal classification (MUSIC)[4], ROOT-MUSIC[5], and estimation of signal parameters via rotational invariance techniques (ESPRIT)[6]. Capon minimum variance is based on the maximum likelihood criterion and it needs to invert the correlation matrix of the received signal. MUSIC performs matrix eigenvalue decomposition according to the orthogonality of signal subspace and noise subspace to avoid matrix inversion. For the extremely high computational complexity of MUSIC，ROOT-MUSIC replaces spectral peak search with polynomial roots. ESPRIT estimates DOA via the rotational invariance of subspace, which further reduces the computational complexity.

Compared with blind DOA estimation methods, the computational complexity of non-blind DOA estimation methods is lower, which can meet the requirements for the rapid positioning of mobile terminals. Non-blind DOA estimation methods mainly include least mean square (LMS)[7]and recursive least square (RLS)[8]. LMS is a simplified one of the steepest descent method, which is based on the minimum mean square error (MMSE) criterion. LMS has the characteristics of simple implementation, low computational complexity and strong anti-interference in multi-path. RLS is proposed based on the least squares (LS) criterion. Compared with LMS, RLS converges faster, but the computation is more complex. In this paper, a new variable step-size LMS method is proposed and applied to estimate the DOA of orthogonal frequency division multiple access (OFDMA)[9]signals. Based on the LMS, a non-blind DOA estimation system for OFDMA signals is constructed. The comprehensive simulation of its performance is carried out in the scenario where interference signals from multi-source and multi-path fading signals arrive at the third-party devices asynchronously with the target signal.

1 A New Variable Step-Size LMS Method

1.1 LMS

The adaptive antenna system is shown in Fig.1. In Fig.1,x(n)={x1(n),x2(n),…xP(n)}Tis the input signal of the adaptive antenna system, whiley(n) is the output signal.

y(n)=wTx(n)

(1)

wherewis the weight vector of adaptive antenna array.

Fig.1 Adaptive antenna system

d(n) is the reference signal ande(n) is the maladjustment betweend(n) andy(n).

e(n)=d(n)-y(n)

(2)

The mean square error is defined as

J=E[|e(n)|2]=E[{d(n)-y(n)}{d(n)-y(n)}*]

(3)

According to the minimum mean square error criterion, the optimal weight vectorwoptis obtained when

(4)

Substituting Eq.(3) into Eq.(4), we can obtain

E[d(n)x*(n)]-E[x(n)x*(n)]wopt=

rxd-Rxxwopt=0

(5)

whereRxxis the auto-correlation matrix ofx(n), whilerxdis the cross-correlation matrix ofx(n) andd(n). WhenRxxis full rank,

(6)

The steepest descent method applies iterations to obtainwopt. In the (k+1)-th iteration, a correction Δwkis added towk, makingwk+1closer towopt.

wk+1=wk+Δwk

(7)

The negative gradient is the direction, in which the objective function declines fast. Therefore,

(8)

whereμis the step-size of adjustment.

In LMS, the current sample is utilized to estimate the negative gradient.

(9)

The steps of LMS are summarized. First, initializew0to0. Then, start the algorithm withn=1. Each iteration of LMS can be divided into three steps:1)e(n) is calculated according to Eq.(1) and Eq.(2); 2) Updatewaccording to Eq.(7) and Eq.(9); 3) Ifnis greater than the total number of iterations, the algorithm is terminated andwnis the optimal weight vector. Otherwise, proceed to the next iteration withn=n+1.

1.2 Logarithmic-sigmod variable step-size LMS

The traditional fixed-step LMS converges when the step-sizeμsatisfies

(10)

whereλmaxis the maximum eigen value of the auto-correlation matrix of the received signal. The steady state maladjustment of LMS results in the obtained weight vector being only an approximation of the optimal weight vector. The convergence speed of LMS is proportional toμ, while the steady state maladjustment is inversely proportional toμ. To meet the above requirement, the step-size needs to be controlled.

A recommended solution is to adopt a variable step-size LMS to achieve both a high convergence speed and low steady state maladjustment.

Sigmod variable step-size LMS (SVS-LMS)[10]definesμas the sigmoid function ofe(n).

μ(n)=β(1/(1+exp(-α|e(n)|))-0.5)

(11)

SVS-LMS converges faster than fixed-step LMS. However,μof SVS-LMS varies greatly whene(n) is close to zero.

Logarithmic variable step-size LMS (log-LMS)[11]definesμas the logarithmic function ofe(n).

μ(n)=blg(a|e(n)|m)

(12)

By combining the two methods above, a new variable step-size LMS is proposed, which is called logarithmic-sigmoid variable step-size LMS (LG-SVSLMS). The step factor updating formula can be set up as

μ(n)=βlg(2-exp(-α|e(n)|m))

(13)

whereαinfluences the overall shape of the curve;minfluences the trend at the bottom of the curve andβinfluences the magnitude of the curve.

LG-SVSLMS overcomes the shortcomings of SVSLMS and Log-LMS. In the initial stage of LMS,e(n) andμare both large. Ase(n) decreases,μdecreases rapidly. In the steady state phase of LMS,e(n) is close to 0 andμis slowly changed. Whene(n) is equal to 0,μalso equals 0, as shown in Fig.2.

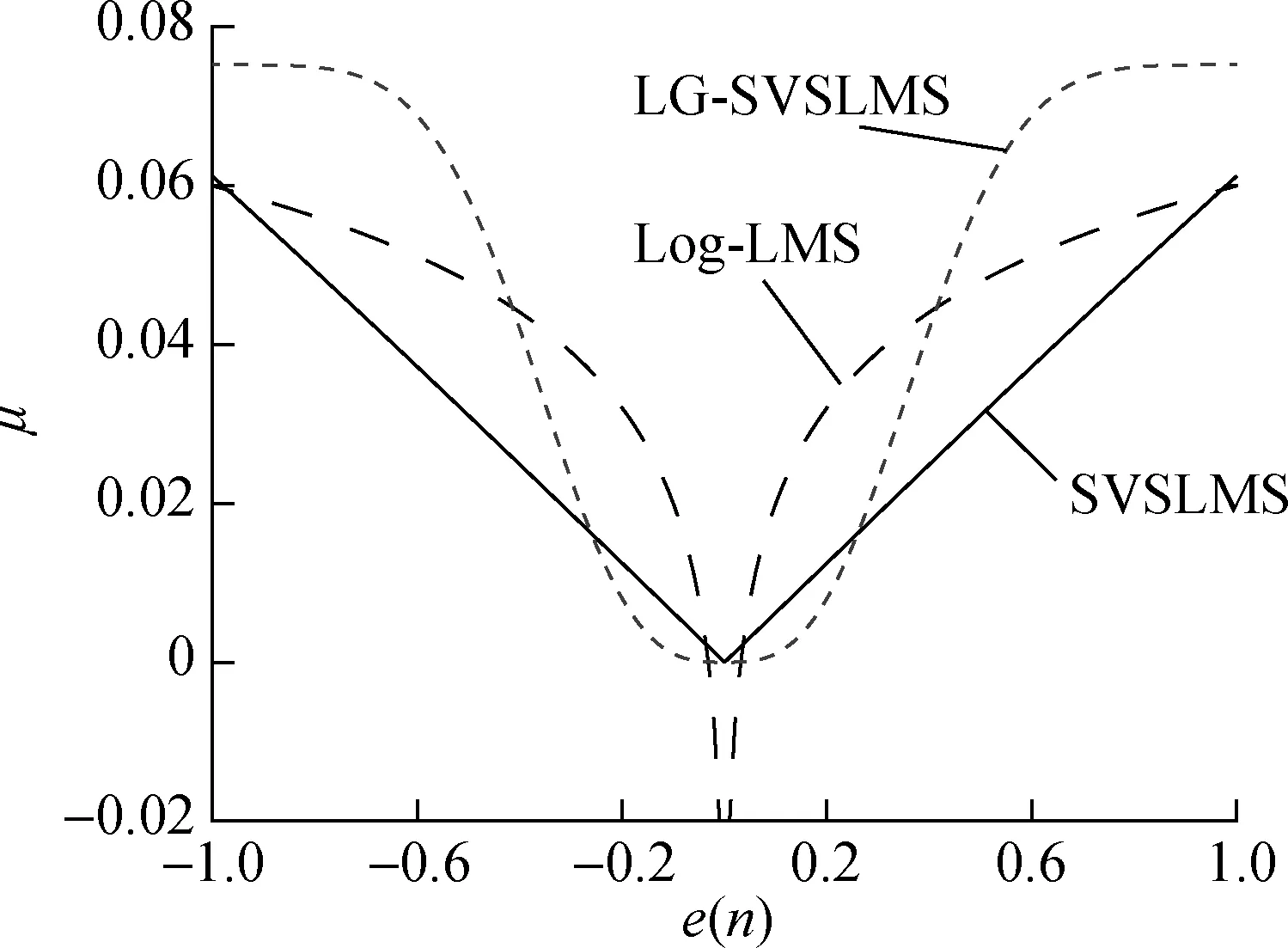
Fig.2 Curve of μ(e) in SVSLMS, Log-LMS and LG-SVSLMS

The steps of LG-SVSLMS are summarized. First, initializew0to0. Then, start the algorithm withn=1. Each iteration of LG-SVSLMS can be divided into four steps: 1)e(n) is calculated according to Eq.(1) and Eq.(2); 2) Calculateμ(n) according to Eq.(13); 3) Updatew; 4) Ifnis greater than the total number of iterations, the algorithm is terminated andwnis the optimal weight vector. Otherwise, proceed to the next iteration withn=n+1.

2 Non-Blind DOA Estimation System for OFDMA Signals Based on LG-SVSLMS

2.1 System flow

OFDMA is the dominant multiple access technology adopted in the 4th and 5th generation communication systems. With mutually orthogonal sub-carriers, orthogonal frequency division multiplexing (OFDM)[12]allows sub-carriers to overlap each other, and avoids the large guard interval between adjacent sub-carriers, which greatly improves spectrum utilization. Different sub-carriers are allocated to different users in OFDMA.

In this paper, a non-blind DOA estimation system for OFDMA signals based on LG-SVSLMS is constructed, which is shown in Fig.3. The system adopts the domain signal of the demodulation reference signal (DMRS) as the reference signald(n).

Fig.3 Non-blind DOA estimation system for OFDMA signals based on LG-SVSLMS

x(n) is the received signal of the uniform linear array (ULA), consisting of direct path signals and multi-path fading signals from multiple UEs. According to the auto-correlation and cross-correlation properties of DMRS, the correlation spectrum ofd(n) andx(n) can be calculated in turn and the effective signal can be extracted from the index of the peak.

Assuming that the array hasPantennas,MUEs propagate signals simultaneously, and there areKmmulti-path signals for each UE. As a result,x(n)={x1(n),x2(n),…,xP(n)}Tcan be defined as follows:

i=1,2,…,P

(14)

wherexi(n) is the received signal of thei-th antenna;vi(n) is the additive white Gaussian noise;ai(θ) is the direction factor of thei-th antenna;dm(n) is the DMRS of UEm; UE 1 is the target user;θmis the azimuth ofdm(n), whileθm,kis the azimuth of thek-th multi-path ofdm(n);nmis the delay of UEmrelative to UE 1, whilenm,kis the delay of thek-th multi-path of UEmrelative to UE 1;lmis the path loss coefficient ofdm(n), andlm,kis the multi-path fading coefficient ofdm(n-nm,k).

Eq.(14) can be represented as

x(n)=Ad(n)+v(n)

(15)

where

x(n)={x1(n),x2(n),…,xP(n)}T

(16)

v(n)={v1(n),v2(n),…,vP(n)}T

(17)

d(n)={d1(n),d1(n-n1,1),…,d1(n-n1,K1),…,dM(n-nM),dM(n-nM,1),…,dM(n-nM,KM)}T

(18)

A(n)={a(θ1),a(θ1,1),…,a(θ1,K1),…,a(θM),a(θM,1),…,a(θM,KM)}

(19)

and

a(θ)={a1(θ),a2(θ),…,aP(θ)}T

(20)

In the same cell, different UEs occupy different sub-carriers. Therefore, the effective part ofx(n) can be extracted from the frequency domain according to the sub-carriers occupied byd1(n).

Then, the extracted signal is converted to the time domain for LG-SVSLMS. The optimal weight vectorwoptmakes

(21)

The direction spectrumP(θ) is defined as follows:

P(θ)=|wHa(θ)|2θ∈(-90°,90°]

(22)

θr=argmaxP(θ) is the estimated DOA of target signal andθe=θr-θ1is the estimation deviation.

2.2 Problems of DOA estimation from third-party devices

Due to the mechanism of time advance established between BS and UEs, the BS can synchronously receive the uplink signals from multiple UEs. However, this synchronization mechanism cannot be established in third-party devices. Therefore, uplink signals from multiple UEs arrive at third-party devices asynchronously, which will make the multiple signals overlap in the time domain, thereby affecting the estimation of DOA of the target signal.

In order to improve the utilization efficiency of spectrum resources and increase the number of users in the system, the frequency reuse technology is adopted in the mobile communication system. Therefore, within a certain distance, there are cells that use the same set of frequencies, which are called co-frequency cells. Co-channel interference will occur between co-frequency cells. The BS is deployed at the center of the cell, hence the co-channel interference from the neighboring cells can be ignored. However, the third-party devices are located at the non-center or even edge of the cell. Therefore, the co-channel interference should be considered in the DOA estimation from third-party devices.

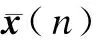
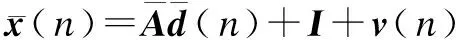
(23)

3 Simulation Results

3.1 Performance of LG-SVSLMS

In this section, the performance of LG-SVSLMS is investigated and compared with SVSLMS and Log-LMS.

The simulation system adopts an adaptive filter with an order of 2. The input signalx(n) is Gaussian white noise with zero mean and unit variance. The noisev(n) is Gaussian white noise with the variance of 0.04, and it is uncorrelated withx(n). The coefficient vector of the finite-length unit impulse response of an unknown system isw={0.8,0.5}T.

Fig.4 shows the curve ofμin different variable step-size LMS. At a steady state, the step size of LG-SVSLMS is greater than that of SVSLMS and Log-LMS, indicating that LG-SVSLMS has the lowest steady state maladjustment in these three methods.

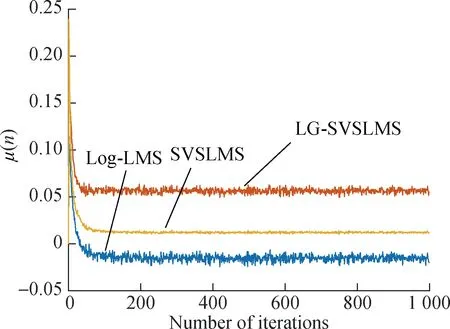
Fig.4 Curve of μ in different variable step-size LMS

Fig.5 shows the curve ofe(n) in different LMS methods. As shown in Fig.(5), the fixed-step LMS converges from the 330th sampling point, SVS-LMS converges from the 120th sampling point, Log-LMS converges from the 100th sampling point, and LG-SVSLMS converges from the 50th sampling point. It can be concluded that LG-SVSLMS has a low steady state maladjustment and a high convergence speed.

Fig.5 Curve of e(n) in different LMS algorithms

3.2 Performance comparison between LG-SVSLMS and MUSIC

In this section, the performance of MUSIC and LG-SVSLMS is compared with each other.

First, the scenario of only one target source with the azimuth of 30° is investigated. As shown in Fig.6 and Fig.7, both MUSIC and LG-SVSLMS can estimate the DOA of the single target UE without bias.

Fig.6 MUSIC spectrum of a single source

Fig.7 LG-SVSLMS direction power spectrum of a single source

Secondly, the scenario of multiple coherent sources is investigated. The azimuth of the target source is still 30°, while the azimuths of the two coherent sources are -18° and -60°.

According to Fig.8 and Fig.9, MUSIC is not comparable to LG-SVSLMS for estimating DOA of multiple coherent sources, because the spatial covariance matrix of multiple coherent signals is not full rank.

Fig.9 LG-SVSLMS direction power spectrum of multiple coherent sources

Finally, the computational complexity of MUSIC and LG-SVSLMS is compared with each other. Assume that the number of antennas isP. MUSIC requiresP2Ladditions andP2L+TPmultiplications, whereLis the number of snapshots andTis related to the estimation accuracy of MUSIC. LG-SVSLMS requiresQPadditions andQP+QJmultiplications, whereQis the length of DMRS andJis the number of iterations when extracting signals.

When the antenna array can effectively receive signals,Jwill be greatly reduced, and the computational complexity of LG-SVSLMS will be much smaller than that of MUSIC.

3.3 Performance of non-blind DOA estimation for OFDMA signals based on LG-SVSLMS

In this section, the performance of the non-blind DOA estimation system for OFDMA signals based on LG-SVSLMS is investigated in the scenario where interference signals from multi-source and multi-path fading signals arrive at the third-party devices asynchronously with the target signal.

This simulation adopts a total of 1 200 sub-carriers, and each UE occupies 48 consecutive sub-carriers. 8 antennas (P=8) are arranged to form a uniform linear array. There are 4 UEs (M=4) within the coverage of the third-party receiver. UE 1, UE 2 and UE 3 are from the same cell, while their DMRS occupies different sub-carriers in the frequency domain. There are two multi-path signals (K1=K2=K3=2) for each UE. UE 4 is from neighboring cell, and its DMRS occupies the same sub-carriers with UE 1. It is assumed that UE 4 has no multi-path interference (K4=0). The signal amplitude of each UE is the same (l1=l2=l3=l4=1), while the amplitude of the multi-path fading signal is 0.55 of the original signal (lm,k=0.55;k=1,2;m=1,2,3).

The azimuth of UE 1 is 30°. The azimuths of UE 2 and UE 3 are -30° and 50°, and the azimuth of UE 4 is 0°. The azimuths of multi-path signals generated randomly.

The performance is investigated by the Monte Carlo method with 200 trials.

The estimation of the DOA of UE 1 with different LMS methods is shown in Fig.10. The direction spectrum of these three LMS methods reach a peak near the target direction. According to Tab.1, the maladjustment of DOA estimation is within ±3°. From the side lobes of spectrum, it can be seen that the side lobe amplitudes of these three LMS methods are close.

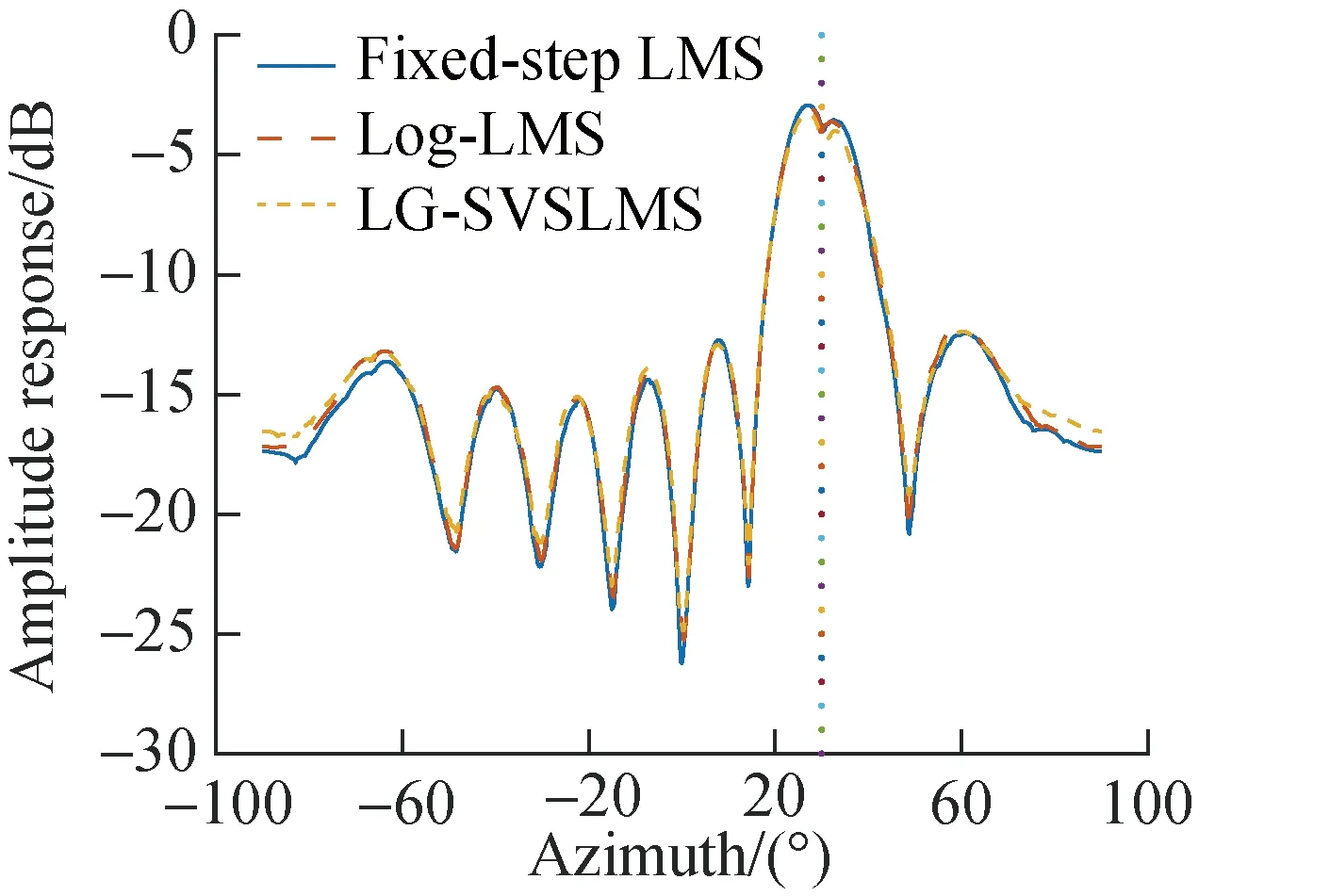
Fig.10 Direction spectrum of non-blind DOA estimation with different LMS methods

Tab.1 Estimation results of non-blind DOA estimation with different LMS methods

Fig.11 shows the curves ofe(n) of non-blind DOA estimation with different LMS methods.Among these three methods, LG-SVSLMS converges first, and the steady state maladjustment is smaller than Log-LMS and fixed-step LMS.

Fig.11 Curves of e(n) of non-blind DOA estimation with different LMS methods

4 Conclusions

1) A new variable step-size LMS method, called LG-SVSLMS, is proposed and applied to estimate the DOA of OFDMA signals. The simulation results show that the LG-SVSLMS can improve the convergence speed and reduce the steady state maladjustment significantly.

2) The performance of the LG-SVSLMS and MUSIC are compared through analysis and simulation. The simulation results show that the LG-SVSLMS can estimate DOAs of multiple coherent sources and its computational complexity is lower than MUSIC.

3) Based on the LG-SVSLMS, a non-blind DOA estimation system for OFDMA signals is constructed and the comprehensive performance simulation is carried out. The simulation results show that the non-blind DOA estimation system based on the LG-SVSLMS can accurately estimate the DOA of the target signal in the scenario where interference signals from multi-source and multi-path fading signals arrive at the third-party devices asynchronously with target signal.