非高斯噪声下基于有界非线性函数的快速盲均衡方法*

王 壮

（南京邮电大学，江苏 南京 210000）

0 引言

随着无线数据流量和干扰的爆炸性增长，电磁环境变得越来越复杂[1]。在这样的电磁环境中，由于多径传播和非理想信道特性，很容易引起符号间干扰（InterSymbol Interference，ISI），严重恶化接收信号的质量[2]。这种情况下，即使没有任何训练信号，盲均衡也被广泛应用于消除ISI 和提高通信质量。在传统的盲均衡方法中，信道噪声通常被假定为高斯噪声。然而，这种假设在复杂的电磁环境中是不现实的[3]。由于自然或人为信号源的影响，信道噪声通常伴随着脉冲特性，如突然爆发和尖峰脉冲[4]。因此，采用加性高斯白噪声（Additive White Gaussian Noise，AWGN）作为信道噪声模型是不合适的。在非高斯噪声环境下，常规的盲均衡方法会使性能严重下降，且鲁棒快速盲均衡仍然是一个挑战。

为了处理非高斯噪声，文献[5]提出了一种广义恒模算法，其中分数阶低阶统计量用于抑制非高斯噪声。文献[6]采用自适应加权系数的方法减少非高斯噪声。文献[7]提出了一种抑制非高斯噪声的鲁棒自适应加权多模数算法。文献[8]提出了一种变步长的改进盲均衡方法。虽然上述盲均衡方法可以抑制非高斯噪声，但它们的性能尤其是收敛速度仍然需要进一步改进。最近，为了消除非高斯噪声的影响，出现了一种被称为有界非线性函数（Bounded Nonlinear Function，BNF）的新概念。与其他去噪方法相比，BNF 可以有效消除非高斯噪声而无需使用先验知识[9]，但它在通信中的应用仍然受到限制。本文尝试将其应用扩展到盲均衡，以便在抑制非高斯噪声方面发挥优势。同时，考虑到传统的盲均衡中的迭代方法在收敛速度上存在弊端，因此采用拟牛顿法加快收敛速度，取得了良好效果。

基于BNF 和拟牛顿法，本文提出了一种在非高斯噪声下鲁棒且快速的盲均衡算法。首先，利用基于BNF 的代价函数有效消除非高斯噪声的影响。其次，采用拟牛顿法提高收敛速度和精度。理论分析表明，所提算法具有鲁棒的收敛性能。仿真结果也表明，该算法在非高斯噪声环境下具有优异的性能。

1 系统模型和前提条件

考虑一个典型的频率平坦衰落信道，假定接收信号时间同步，然后在时刻n上的基带接收信号为：

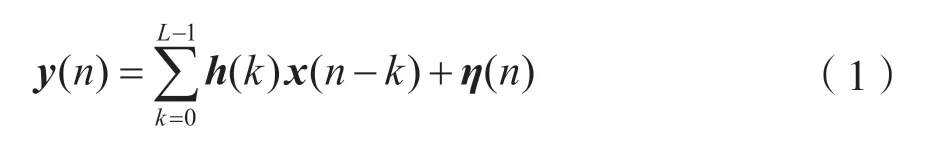
其中y(n)是接收信号，也是盲均衡器的输入信号。h(k)表示具有L阶的信道脉冲响应，x(n)表示发送的数据序列。η(n)=Re[η(n)]+jIm[η(n)]是加性复合非高斯噪声，通常由α稳定分布[10]建模。由于α稳定分布不具有概率密度函数的封闭形式[4]，所以它的特征函数通常表示为：

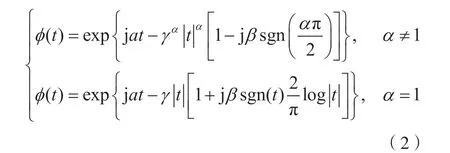
其中γ∈(0,+∞)是对称参数，β∈[-1,1]是位置参数，α∈(-∞,+∞)表示特征指数，决定了密度函数的冲动性水平。α∈(0,2]表示确定密度函数的脉冲水平的特征指数。当α＜2 时，在这种噪声环境下会有许多尖锐的脉冲，此时盲均衡的输出可以表示为：

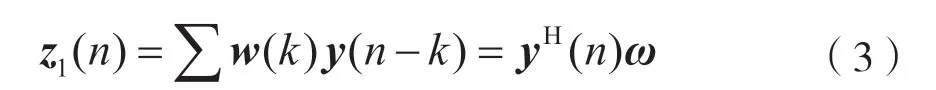
其中ω=[w(0),w(1),…,w(m-1)]表示盲均衡的抽头系数，阶数为m，z1(n)表示盲均衡的输出信号，y(n)=[y(n),y(n-1),…,y(n-m+1)]T表示输入向量。

盲均衡的目的是消除接收信号y(n)中的ISI 和噪声影响，并进一步恢复发送序列x(n)。然而，在非高斯噪声环境中，当α＜2 时，这种分布将不存在二阶及高阶统计量。因此，传统的基于二次统计量或均方误差（Mean Square Error，MSE）准则的盲均衡方法在非高斯噪声环境下严重退化，甚至无法实现均衡。

2 提出BNF-NL-CMA 算法

对于传统的盲均衡器，CMA 可能是应用最广泛的方法，因为其简单、稳定[6]。CMA 的成本函数表述为：

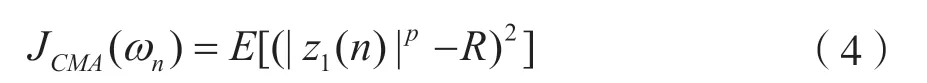
其中p＞0 是一个整数，R=E[|x(n)|2p]/E[|x(n)|p]。此外，在梯度下降法的基础上，可以将ωn的更新公式定义为：

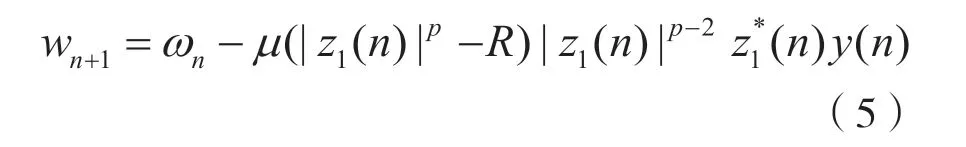
其中μ是步长。由式（4）和式（5）易知，高阶统计量(|z1(n)|p-R)2包含在代价函数中，这将放大非高斯噪声中大离群点的影响，并进一步导致盲均衡中严重的失调。BNF 可以有效消除脉冲噪声，特别是对于非高斯噪声中的较大异常值。因此，基于BNF 设计了一种新颖的盲均衡算法，以减轻非高斯噪声引起的退化。

首先，将BNF 定义为：

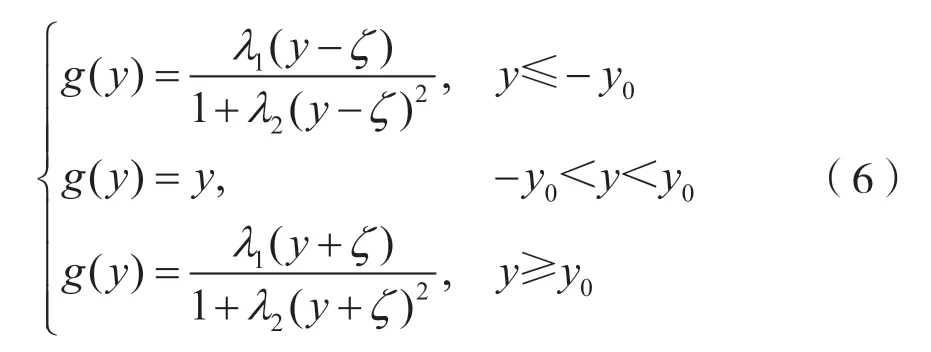
其中y0、ζ、λ1和λ2是可调参数。为了更清楚地说明BNFg(y)，举例来说，当y0＝2.2、ζ=16.3、λ1＝1.06、λ2＝0.025 6 时，BNF 的曲线如图1 所示。图1 中能够明显看出g(y)是一个有界函数。当y∉(-y0,y0)时，g(y)为非线性的；当y∈(-y0,y0)时，g(y)=y是一个完美的线性函数。如图1 所示，非高斯噪声中的脉冲部分可以通过非线性有界来抑制，同时可以通过BNF 中的线性部分保持接收信号的原始信息，包括信道信息。因此，BNF 的使用对接收信号的信息损失很小。此外，所提出的成本函数定义为：

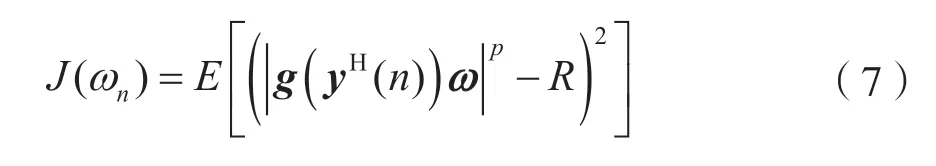
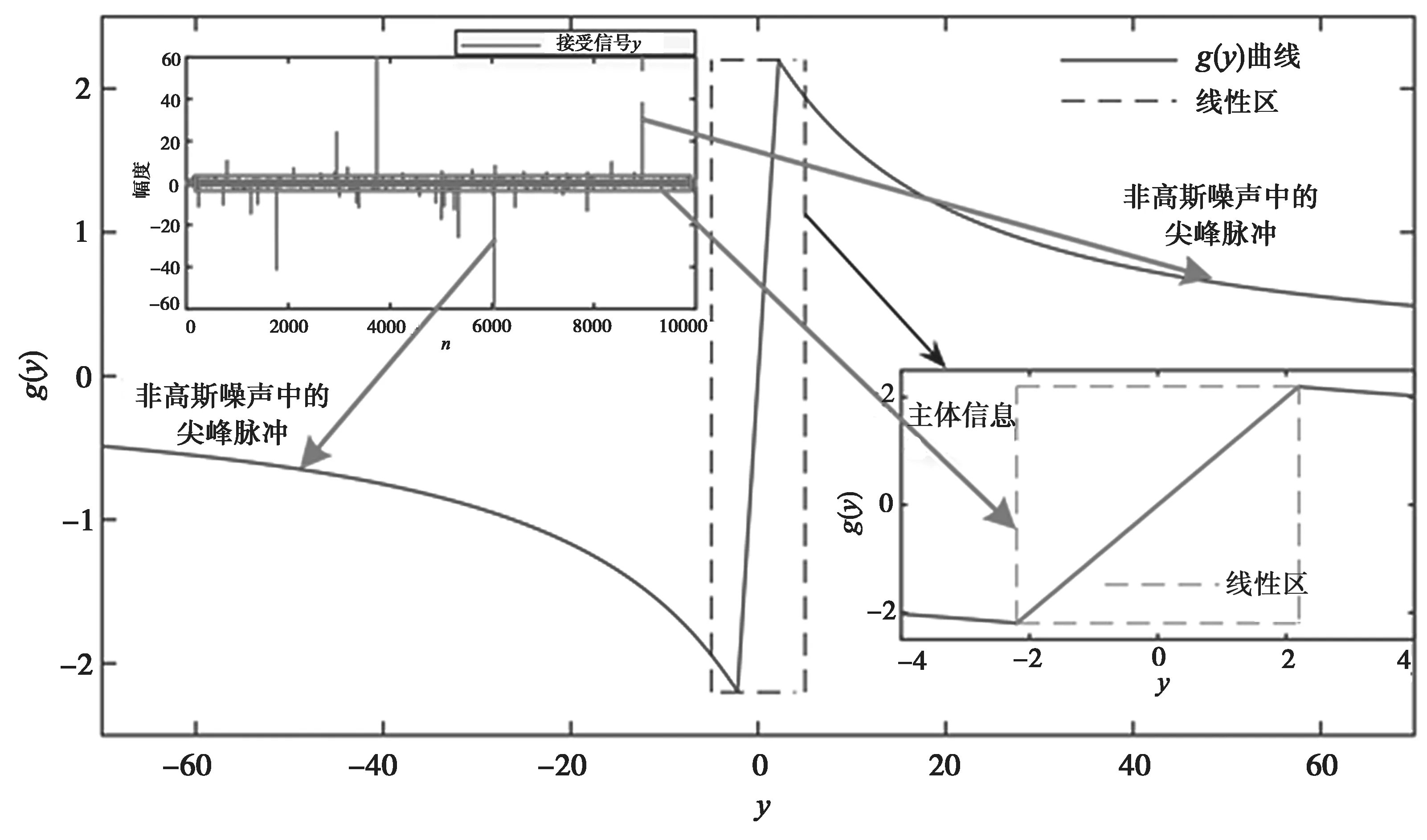
图1 BNF 曲线

如式（5）所示，传统的盲均衡器通常采用梯度下降法，收敛速度较慢，特别是与拟牛顿法相比。为了加快收敛速度，提出的盲均衡算法采用了拟牛顿法，然后将其权重向量的更新公式定义为：

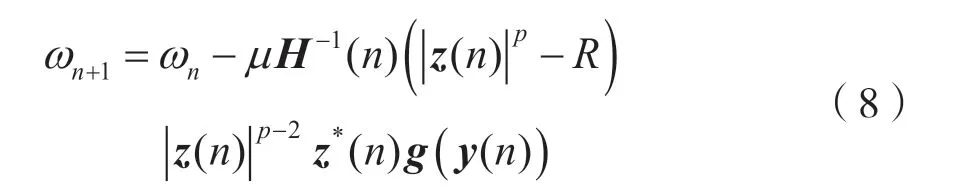
其中z(n)被定义为z(n)=g(yH(n))ω。此外，H(n)为Hessian 矩阵，定义如下：

其中函数D定义为：

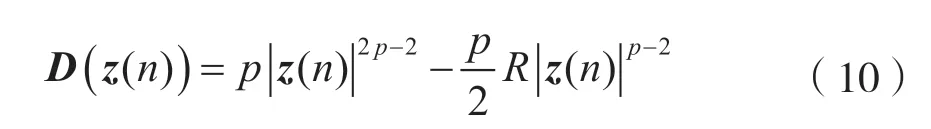
实践中，可以通过联合式（11）估算式（9）中的期望值，其中λ∈(0,1)：

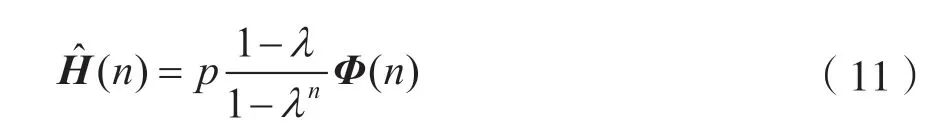
其中，Φ(n)为：

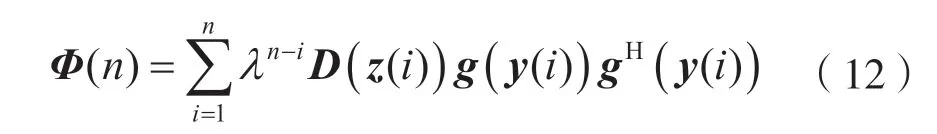
同时，Φ(n)还满足以下的性质：

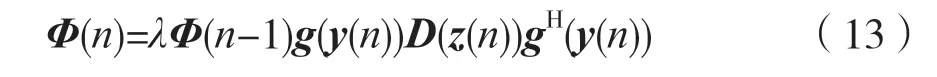
此外，可以得到它的逆矩阵Q(n)=Φ-1(n)的递推方程：

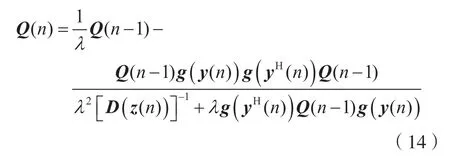
因此，Hessian 矩阵H(n)的逆可以写成：

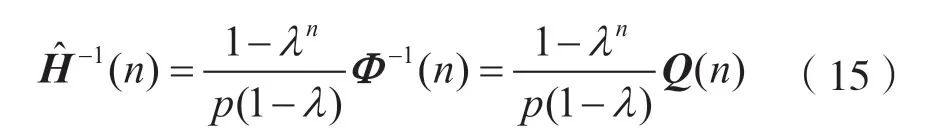
最后，通过上述分析可以得到更新算法的公式：

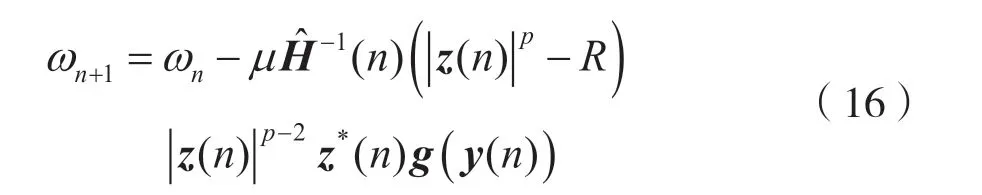
其中μ是一个常数，表示步长。与传统的盲均衡算法相比，该算法由于利用了BNF，可以有效消除非高斯噪声的影响，采用拟牛顿法大大加快了收敛速度。

3 收敛性能分析

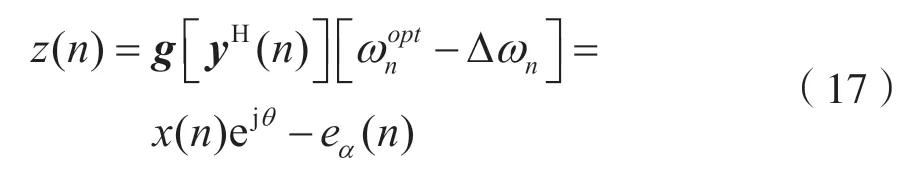
其中：eα(n)=g[yH(n)]Δωn表示先验估计误差；θ为常数，通常设置为0。本文使用稳态均方误差（MSE）测量均衡器性能，表示为。式（8）中，两边同时减去ωopt(n)，则有：

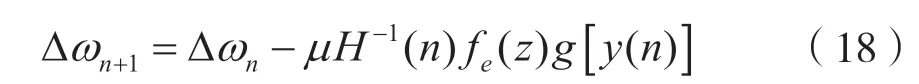
其中fe(z)=(|z(n)|p-R)|z(n)|p-2z*(n)。然后，式（18）两边同时乘gH(y(i))，得到：

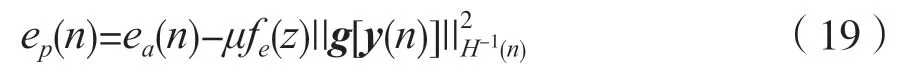
其中，ep(n)=gH[y(n)]Δωn表示后验估计误差，其中运算符定义为：

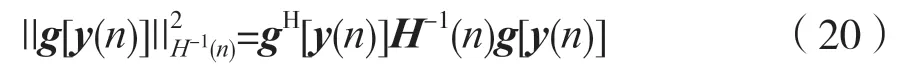
此外，根据文献[11]，式（8）的能量守恒关系式可以表示为：

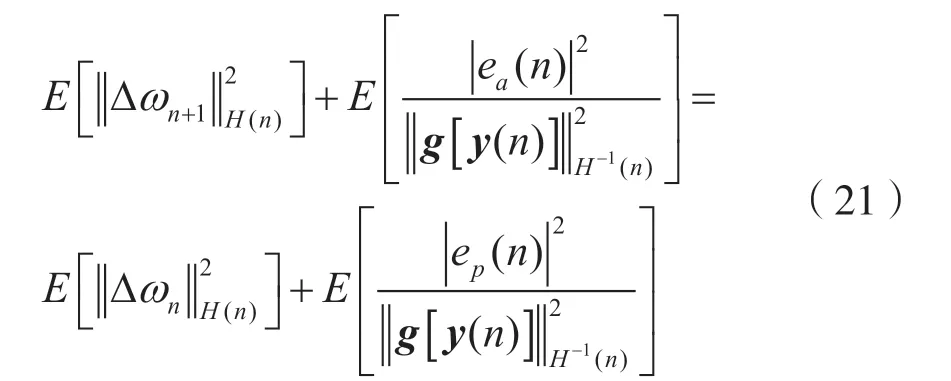
在n→∞时，均衡器将运行在稳态状态E[||Δωn+1。文献[11]中为了不失一般性，还假设输入向量的能量与fe(z)独立，然后将等式（19）代入式（21），简化后得到：

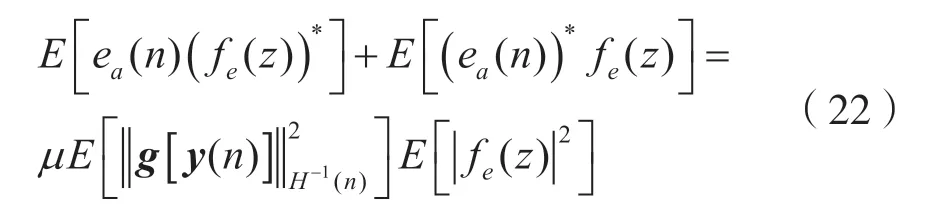
为了简单起见，用它在点x的二阶泰勒级数展开式代替fe(z)，为：

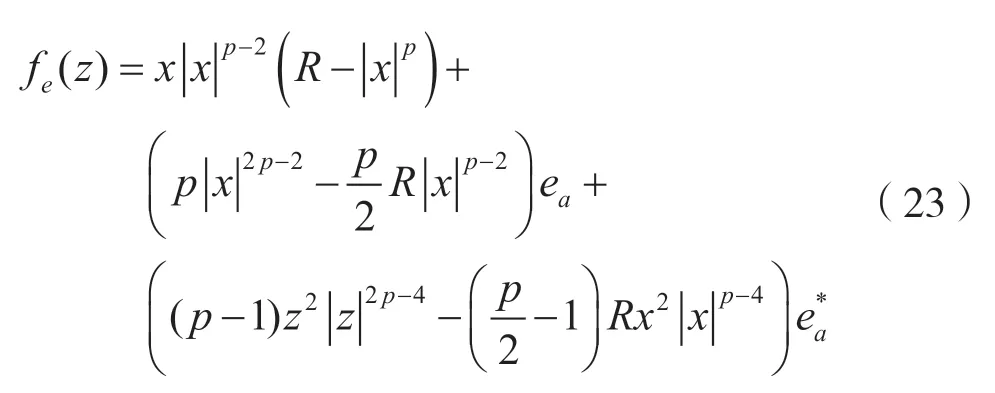
此外，文献[11]中还有一个假设E[x(n)]=0，在圆度信号条件下，复数信号x(n)满足E[x2(n)]，联立式（22）和式（23）可以得到：

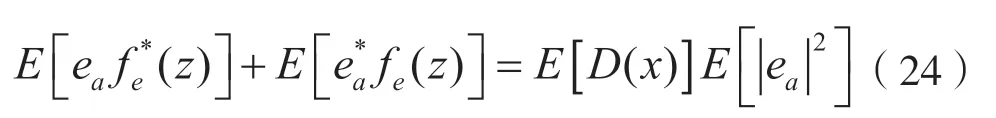
对于等式（22）的右边，在等式（12）的基础上可以得到E[Φ(n)]的近似公式：

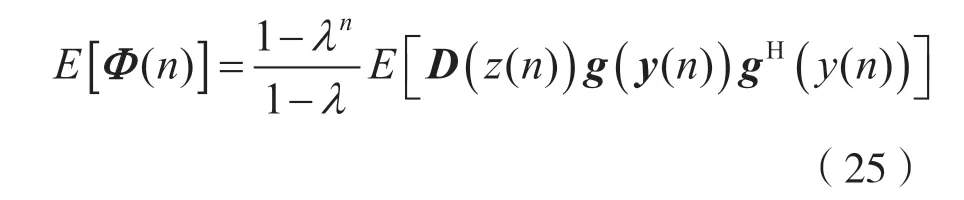
然后，将式（15）和式（25）代入式（20），得到：

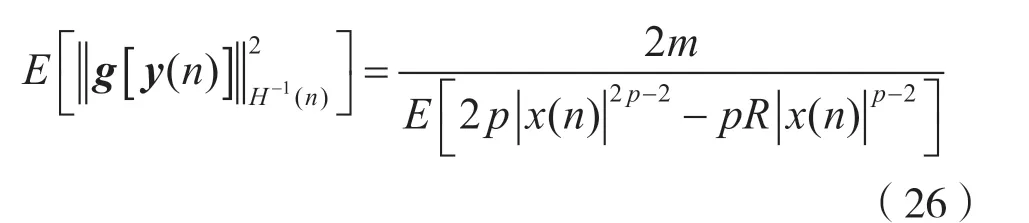
其中m表示盲均衡器的长度。

最后，将式（23）、式（24）、式（26）代入到式（22），得到MSE 的公式：

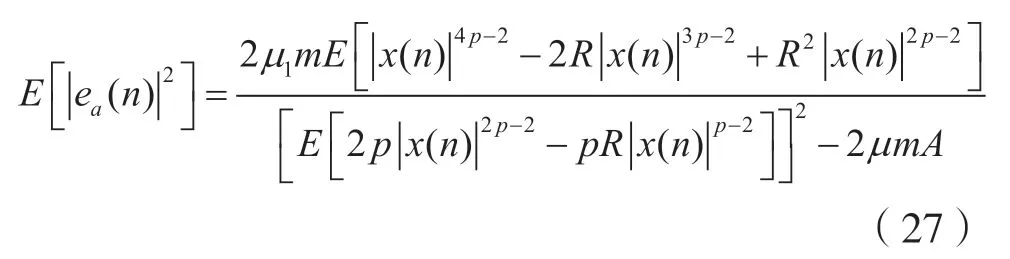
其中，参数A定义为：

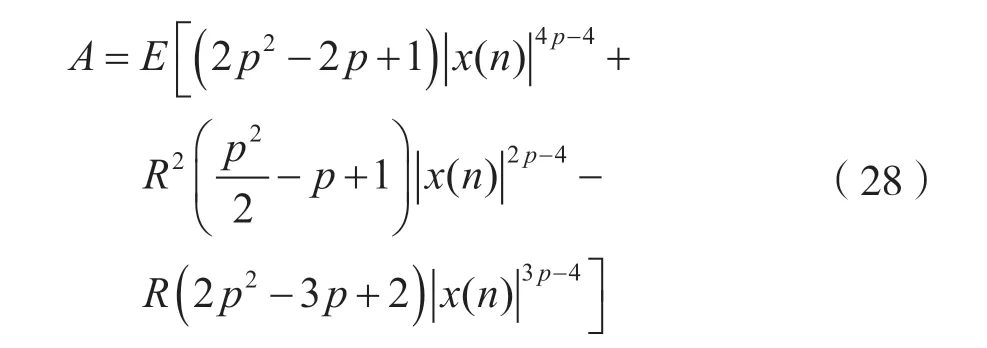
显然，对于给定的盲均衡器，所提方法的稳态MSE 主要由步长μ1和长度m控制。因此，提出的算法是收敛的。

4 仿真结果

通过蒙特卡洛仿真对非高斯噪声环境下的盲均衡方法和其他对比方法进行评价。这些方法的性能由MSE 和符号间干扰（ISI）衡量。

ISI 定义为：

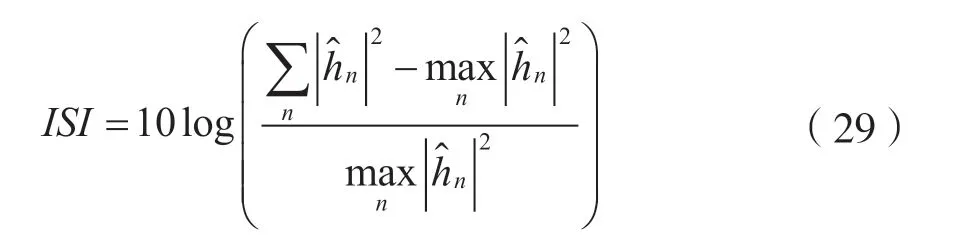
如图2 所示，用符号错误率（Symbol Error Rate，SER）评估提出的方法的稳态性能。仿真中，α设为1.35，GSNR由18 dB 设置为26 dB。图2 中，与其他对比方法相比，所提方法性能更稳健，且在每个GSNR值上都能达到最低的SER。因此，该方法比其他方法具有更好的稳态性能，能够有效抑制非高斯噪声。

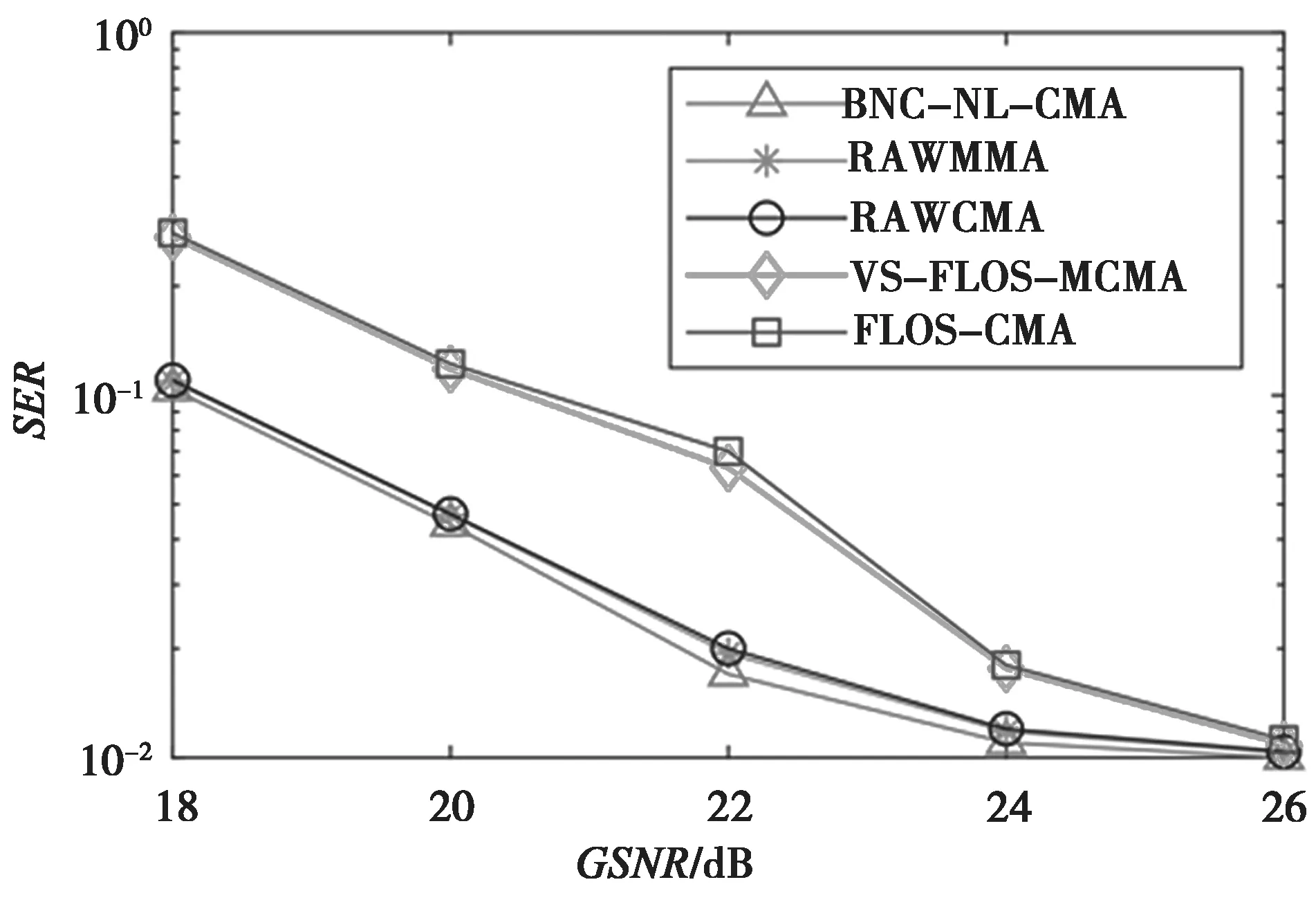
图2 SER 性能比较

然后，用GSNR=26 dB 的ISI 对所提出的方法与其他对比方法的收敛性能进行比较。如图3 所示，当α=1.3 时，所提出的方法可以在不到4 500 次迭代的情况下收敛到稳定状态，而其他对比方法至少需要7 500 次迭代才能达到稳定状态。此外，当这些方法在稳定状态下运行时，所提方法可以收敛到比其他对比方法更小的ISI。

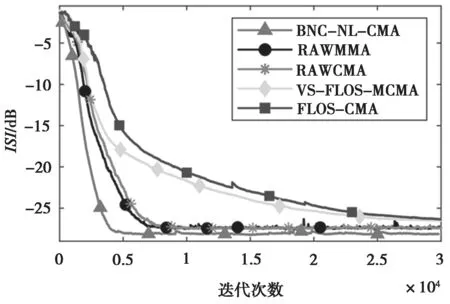
图3 ISI 性能比较

此外，为了评估所提方法在不同步长下的收敛性能，在图4 中给出了不同步长的ISI 曲线。显然，在较大的步长情况下，该方法具有较快的收敛速度。然而，它也有很大的残余ISI，导致均衡性能较差。当步长较小时，可以达到理想的均衡性能，但是此时的收敛速度会较慢。从图4 可以看出，当μ=0.001 15 时，它是均衡性能和收敛速度之间的一个折衷。

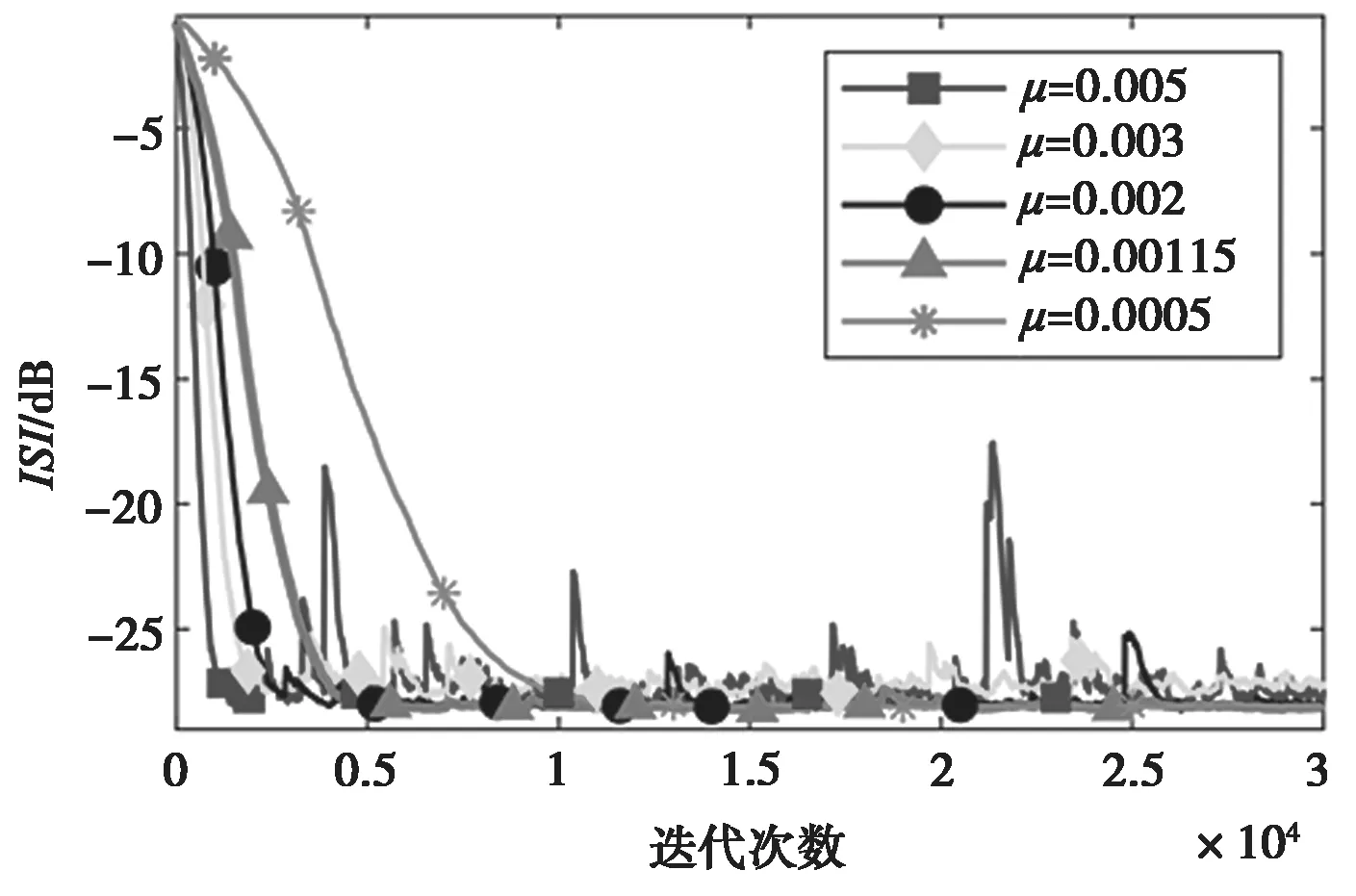
图4 BNC-NL-CMA 在不同步长下的ISI

最后，评估这些方法的计算复杂度。同文献[6]一样，为了不失一般性，本文忽略了这些方法中加法和减法运算的复杂度。假设盲均衡器的阶数是L0，然后对于每个迭代步骤可以得到FLOS-CMA的复杂度约为2L0，RAWMMA 的复杂度约为3L0，所提出方法的复杂度约为5L0。虽然所提方法在每次迭代中的复杂性高，但是需要更少的迭代时间达到稳定状态，因为它具有快速的收敛速度。例如，如图3 所示，为了达到稳定状态，所提方法需要大约4 500 次迭代时间，而VS-FLOS-MCMA和RAWMMA 方法分别需要7 500 次和25 000 次迭代时间。经过计算，BNF-NL-CMA、RAWMMA、VS-FLOS-MCMA 的稳态总复杂度分别为22 500L0、22 500L0、50 000L0。因此，与对比方法相比，所提方法的总复度是可以接受的。

5 结语

本文在BNF 和拟牛顿方法的基础上，提出了一种新的非高斯噪声环境下的盲均衡方法。该方法中采用BNF 抑制非高斯噪声，同时将拟牛顿法结合到盲均衡器中，提高了收敛速度，最后推导了MSE以证明所提算法具有鲁棒的收敛性能。通过蒙特卡洛仿真可以发现，所提方法可以在非高斯噪声的情况下达到快速而稳定的性能。