基于改进自回归移动平均算法的能耗预测

刘宏利，高子鹏

（天津理工大学 电气电子工程学院，天津300384）

近年来，由于城市改造进程加快，我国建筑、工程能耗同比增长近30%，加强能源管理，提高能源利用效率，改善能源使用环境成为当前首要任务，因此各地有关部门对能源监测，能耗预测等方面开展深入研究.谢武明等[1]基于BP 神经网络，利用遗传算法优化网络对污水处理厂电耗进行预测；段冠囡[2]提出了一种基于GM-RBF 神经网络的超高层建筑暖通空调能耗预测方法.同时，时间序列分析法作为一种成熟的统计学方法，能源消耗预测等领域有着广泛的应用.黄荣庚等[3]使用ARMA 算法对地铁环控系统进行能耗预测；赵建忠等[4]将小波变化与ARMA 算法相结合预测导弹装备备件需求；曾德明[5]使用BP神经网络与ARMA 相结合的方法预测电力负荷情况等等.在一些特殊研究领域ARMA 也是作为一种必要的预测方法有所应用，如文献[6]中，作者使用ARMA与Kriging 相结合的方式预测土壤盐分变化情况.

由于时间序列分析法在短期、小样本预测中的预测结果更好，实现更方便，所以本文使用时间序列分析法来实现耗能预测，通过改进EMD-ARMA 算法，进而提高预测结果的准确度.

1 数据样本分析

能耗预测的服务对象是建筑群的能耗数据，本文使用的数据样本是某单位办公楼2018 年8 月份的能耗数据，样本数据量31，样本数据见表1.

表1 电能能耗数据样本Tab.1 Sample of energy consumption data

1.1 本征分量提取

由表1 可知，该数据样本不符合平稳时间序列特性，所以该数据样本是不能直接使用ARMA 模型进行建模的.故而要对数据样本进行一定的数据预处理，引入EMD 算法提取原始数据样本的特征分量，进而对特征分量进行ARMA 建模. EMD 算法可将原始的数据样本Q（t）分为有限个具有原始数据样本特征的数据分量样本Ci（t），分解得到的每个分量数据样本都具有一定的原始数据样本特征，分量数据样本能在某方面更显著的反应出原始信号的数据特点.EMD 算法的一般计算过程如以下四个步骤：

1）求取原始数据样本Q（t）的所有极值点（一阶导数为零）.

2）利用三次样条函数，拟合极值点得到上包络和下包络函数，求取上下包络均值M（t）.

3）取H（t），H（t）=Q（t）-M（t）.此时H（t）一般不为平稳数据序列，故此对H（t）重复步骤（1）和（2），直到新的SD（H′（T））的范围在0.2 ～0.3 之间，得到第一个本征分量C1（t）=H′（t）[7].

4）取新的复杂信号R（t），R（t）=Q（t）-H（t）.再对R（t）重复步骤（1）、（2）和（3），得到第二个本征分量C2（t）.重复该过程，直到最后一个数据序列Cn（t）不可被分解，此时该Cn（t）则是代表数据序列的趋势或均值.

原始数据样本经过EMD 分解之后会得到多个平稳时间序列分量，以及一个趋势分量，该趋势分量相对于多个平稳时间序列分量而言一定是一个低频的分量.

1.2 回归分析指标选取

回归是对连续的实数值进行预测，需要回归评估指标来对回归模型进行评价，显示回归模型的有效性与优越性.选取其中使用最为普遍的两个回归评估指标，分别是平均绝对误差（MAE）和均方根误差（RMSE）[8].假设h（i）是预测结果中的第i个预测值，y（i）是数据样本中的第i个真实值，n为预测样本数.

均方根误差是预测值与真实值偏差的平方和与预测次数比值的平方根，用于衡量预测值同真值之间的偏差.

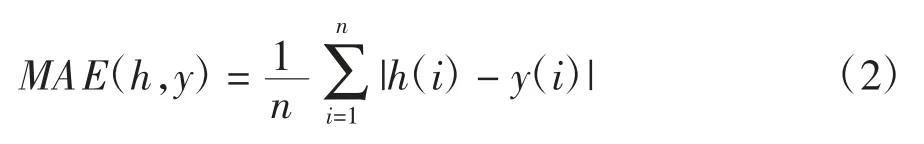
平均绝对误差是绝对误差的平均值，同样是用来衡量观测值同真值之间的偏差.

2 改进预测模型构建

在改进模型构建的过程中，主要用到两个数学模型，即ARMA 模型和多项式模型. 在ARAM 模型构建（即求参）的同时还要考虑到模型定阶的问题.改进模型的总体流程如图1 所示.

图1 本文算法流程图Fig.1 Algorithm flow chart

改进模型首先要将原始数据样本进行EMD 分解，得到各IMF 分量；随后通过对分量信号进行幅值和频率的判断，划分频率阈值将其分为高频特征分量和低频特征分量，然后再利用ARMA 模型和多项式模型对两类分量进行拟合预测，最终将分量预测值叠加，得到预测结果.

2.1 ARMA模型构建

对于高频的平稳时间序列分量，选用ARMA 模型进行分量预测. ARMA 模型由AR 模型和MA 模型两个部分组成，以ARMA（p，q）来说明[9-12]，模型表示为：

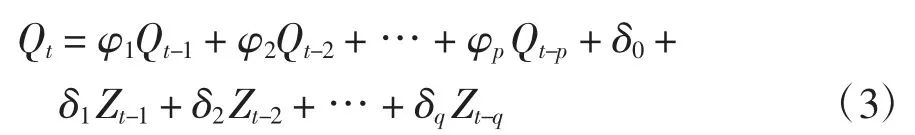
式中，p为自相关阶数；q为偏相关（移动平均）阶数；φ 为自相关系数；δ 为偏相关（移动平均）系数，Q为观测值，Z为误差项.由于误差项在不同时期与Q值具有依存关系，故而Z也可视作相关因素.建立该模型首要面对的问题就是如何根据数据样本求取相关系数，相关系数度量的是同一事件在两个不同时期之间的相关程度，故而φi是由Q（t）与Q（t-i）的协方差所得.

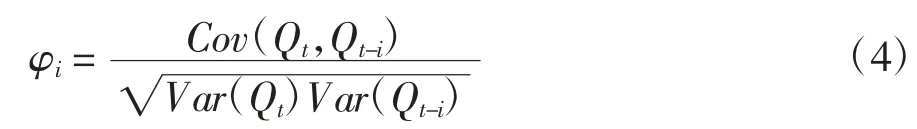
式中，Cov（Q（t）、Q（t-i））是Q（t）与Q（t-i）的协方差；Var（Q（t））是Q（t）序列的方差；Var（Q（t-i））是Q（t-i）序列的方差.偏相关系数与自相关系数求取方式类似.在建模之前，存在一个前置问题即定阶的问题，本文使用的定阶方法是计算AIC 值，利用遍历方式计算AIC 数值，取最小值定阶[8].定阶流程如图2所示.

图2 ARMA 定阶建模流程图Fig.2 ARMA fixed-order modeling flow chart

因为AIC 校验是建立在熵（用来衡量体系混乱程度的度量）的基础上的，因而可以权衡所估计模型的复杂程度和模型拟合数据的优良程度. BIC 考虑的惩罚项要比AIC 多，使用BIC 可以在样本数量过多时，有效防止模型精度过高造成的模型复杂度过高.因为本文的预测对象属于小数据样本，为了精简算法易于实现，单纯计算AIC 值用于定阶.在一般情况下AIC 可以表示为：

式中，k值是参数数量；L为数据样本的似然函数.

2.2 高阶多项式模型及总模型构建

对于低频趋势分量，选用高阶多项式拟合的方式进行预测，求取拟合公式，计算其低频分量的预测结果.低频趋势分量高阶多项式拟合公式：

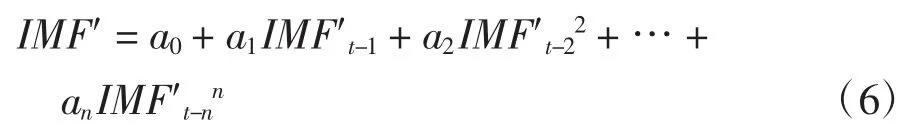
式中，IMF′为低频分量；a为多项式系数. 由式4 可知，高频的平稳时间序列ARMA 模型的拟合公式：

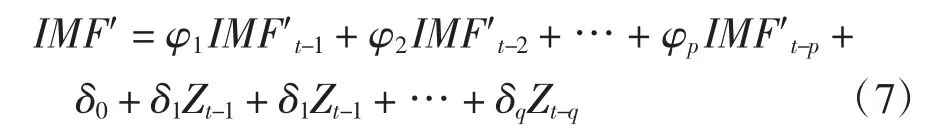
式中，φ 为自回归系数；δ 为偏回归（移动平均）系数，IMF 为高频分量，Z为误差.将各IMF 分量作和，得本文模型的拟合公式：

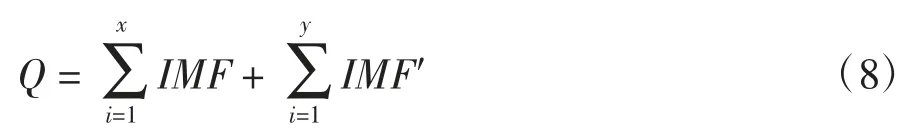
式中，x为高频分量个数；y为低频分量个数.

2.3 多值预测

通过实验，这种预测方式，对于预测值的个数越少越好，因此如果需要进行多天的电能能耗预测，就需要利用预测值来更新数据样本，重新预测新值. 总体预测流程如图3 所示.

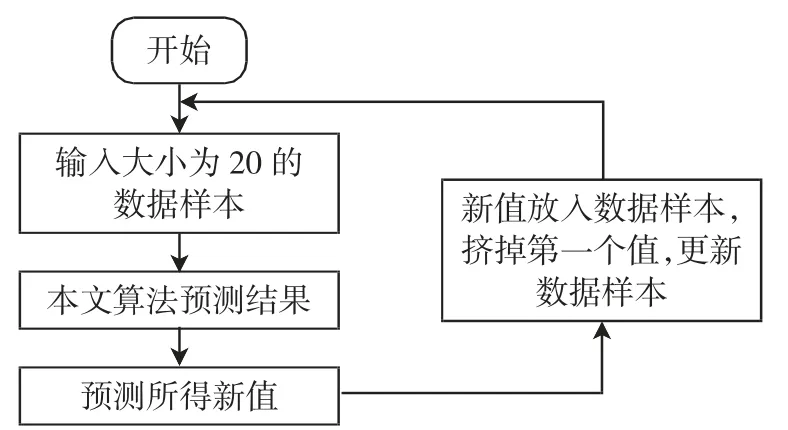
图3 多值预测流程图Fig.3 Flow chart of multi-value prediction

通过实验仿真发现，以这种方式对连续一段时间内数据预测效果更好，只是计算量相对较大，并不适合在控制器上直接实现.

3 仿真实验及效果分析

3.1 仿真实验及结果

本文算法是首先将数据样本进行EMD 分解，最终得到了四个IMF 分量.对其中的高频时间序列分量IMF1、IMF2 和IMF3 结合相关参量建立ARMA 模型，对低频趋势分量IMF4 建立高阶多项式模型，分别计算拟合公式，求取分量预测值.再将分量预测结果合成得到需要的第一个预测结果；求取第一个预测值后，更新数据样本，求取第二个预测值，以此类推，得多值预测结果.

高频分量IMF1 与其ARMA 的预测结果见图4，由图4 可知IMF1 的数据起伏较大. 这是因为EMD算法本身第一个分解出的特征分量是原始数据样本极大值包络和极小值包络的均值线条，该分量的频率相比于其他分量的频率要高，等长取点就意味着数据起伏较大. 低频分量IMF4 与其ARMA 和高阶拟合的预测结果见图5，高阶多项式的预测结果与IMF4 基本重合，要明显优于ARMA 的预测结果.

图4 高频分量IMF1 及拟合Fig.4 IMF1 and fitting

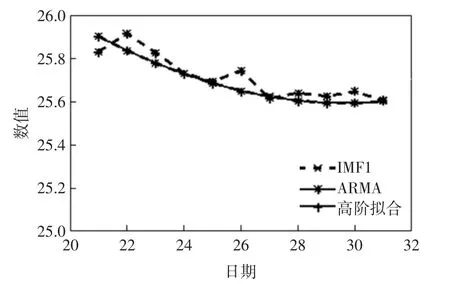
图5 低频分量IMF4 及拟合Fig.5 IMF4 and fitting

从IMF4 的纵坐标处可以看出，尽管使用多项式拟合的方式确实比ARMA 要准确，但是误差很小只有0.1 左右的误差.故而本文算法使用在多点数据预测上还使用2.3 节的多值预测方法，利用计算量换取数据预测精度. 将本文算法与EMD-ARMA 直接预测做比较，预测结果与实际结果见表2，折线图见图6.

在预测多点数据方面，EMD-ARMA 是利用拟合公式直接求取多点对应的预测值，本文算法是更新拟合公式连续只求取下一点的预测值，由图6 可以看出，在未来的时间里增长或下降的幅度将会有所增强.在模型搭建方面，EMD-ARMA 是将经验模态分解算法和ARMA 模型结合，本文算法是将经验模态分解算法、ARMA 模型和多项式模型三者相结合.

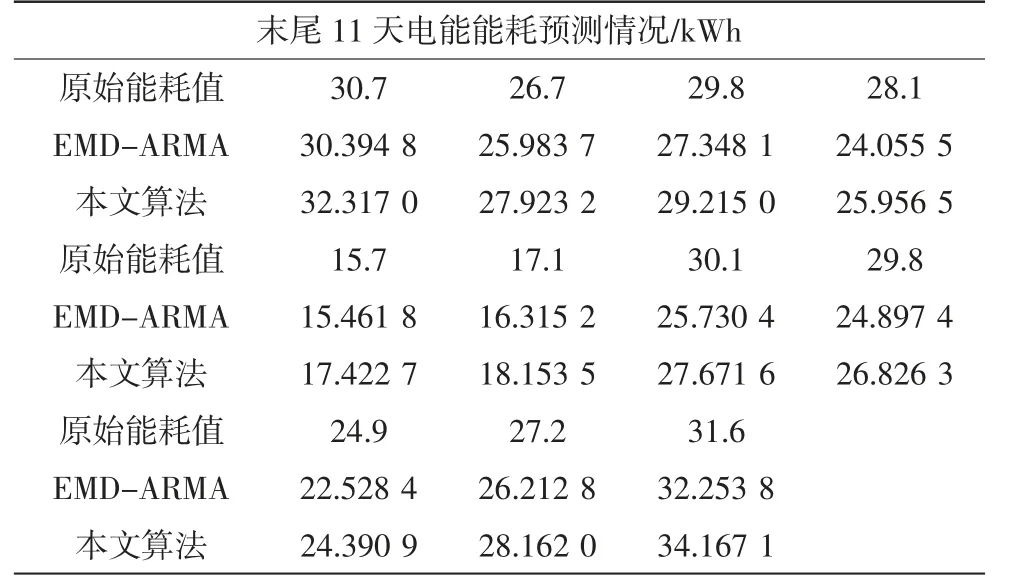
表2 数据样本及各算法预测结果Tab.2 Data samples and prediction results of each algorithm

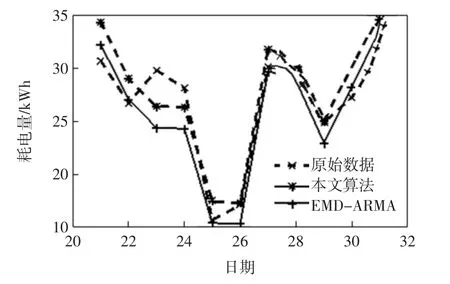
图6 各种算法预测结果折线图Fig.6 Line chart for the result of each algorithm

3.2 效果分析

本文利用利用均方根误差（RMSE）和平均绝对误差（MAE），来分析预测结果的准确性.

由表3 和图6 可知，EMD-ARMA 算法与本文算法相比较相差不多，算法的主要不同之处在多值预测上的方式不同和处理低频分量的方式不同，从而使得预测精度有所提高.在低频分量上选择不同的处理方式，其原因在于ARMA 模型在低频信号的拟合上，不如高阶多项式模型拟合更加平滑，故而EMDARMA 的预测结果不如本文算法的预测结果更加准确. 当然，根据数据样本的不同，经过EMD 分解之后，低频信号也不完全是使用多项式模型拟合最好.有时经EMD 分解后得到的最低频信号也足够“高频”，使用ARMA 模型一样拟合效果很好，甚至要超过高阶多项式模型.故而要以IMF 分量的频率进行判断、分类，从而确定随后的拟合方式.

表3 各算法RMSE 和MAETab.3 RMSE and MAE for the each algorithm

4 结 论

本文算法利用EMD 分解算法，对数据样本进行二次处理，对分解得到IMF 分量进行判别.对低频趋势型的IMF 分量进行高阶多项式拟合，对高频平稳时间序列型的IMF 分量进行ARMA 拟合，综合各IMF 分量得到预测结果. 该算法的优点在对于历史数据样本容量的要求很低，由于具体问题具体分析的原因，预测结果也更为准确.