矮塔斜拉桥结构参数敏感性分析
2020-07-18寇静
寇 静
(西南交通大学土木工程学院桥梁工程系,四川成都 610031)
矮塔斜拉桥是一种介于连续梁桥和斜拉桥之间的桥型,兼有连续梁桥与斜拉桥的优点,且其桥塔刚度较大,桥面连续影响小,适用于多孔斜拉桥,在100~300 m跨径范围内极具竞争力[1-2]。对矮塔斜拉桥的结构参数进行敏感性分析,不同的参数变化对桥梁结构的力学状态的影响程度不同,由此可确定哪些参数为主要敏感性参数,哪些参数为次要敏感性参数。因此,本文以某矮塔斜拉桥为工程背景,建立空间有限元模型,选取主梁混凝土容重、主梁弹性模量、斜拉索弹性模量、主梁预应力荷载等结构参数进行结构静力响应的敏感性分析,为同类桥梁的施工控制提供参考。
1 工程背景及有限元模型
1.1 工程概况
某双塔单索面矮塔斜拉桥,主桥布置为(136+240+136) m,结构体系为塔、墩、梁固结体系(图1)。主梁为单箱三室斜腹板变截面混凝土箱梁,根部梁高8.2 m,端部等截面段梁高为4 m,梁高按二次抛物线变化。主梁采用三向预应力结构,设有纵、横、竖三向预应力,分别布置在主梁内、横隔板内、腹板内。桥塔采用等截面矩形实心断面,桥面以上塔高44 m,布置在中央分隔带上,并与箱梁固结。斜拉索为单索面、双排布置在中央分隔带上,全桥共采用4×12对斜拉索。

图1 桥型立面布置(单位:cm)
1.2 有限元模型
采用有限元软件Midas/Civil 建立该桥有限元模型(图2),全桥共离散为2 213个节点,1 466个单元。主梁、桥塔和桥墩采用六向自由度的空间梁单元模拟,斜拉索采用桁架单元模拟。

图2 有限元模型
1.3 结构参数及其变化幅值
本文研究的结构参数为主梁混凝土容重、主梁弹性模量、斜拉索弹性模量、主梁预应力荷载,其设计值与变化幅值见表1。在忽略收缩徐变的影响的前提下,结构参数在增加或减少相同的变化幅值时,结构产生的同一静力响应的变化量数值几乎相同,符号相反,因此本文只讨论结构参数在设计值基础上增加的情况。
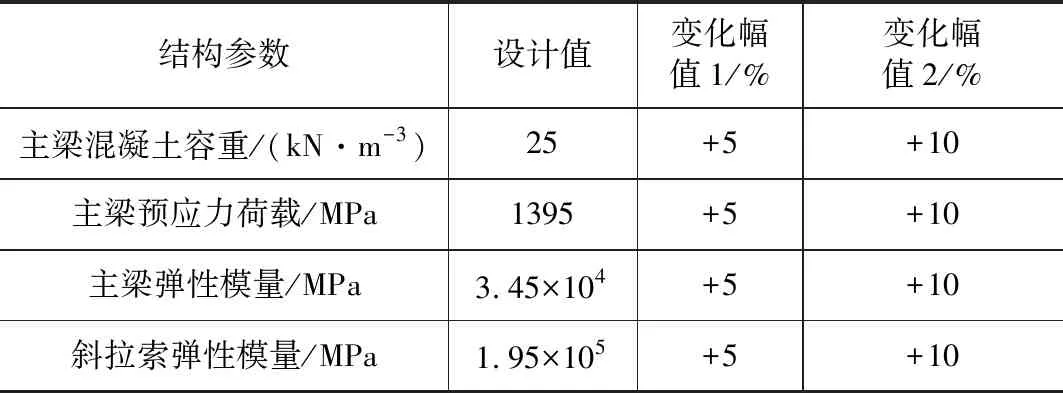
表1 结构参数设计值与其变化幅值
2 结构参数敏感性分析
2.1 主梁混凝土容重
混凝土梁段在浇筑过程中混凝土容重会产生一定误差,也可能由于混凝土超方、模板变形等原因使其截面尺寸产生一定误差。在结构敏感性分析时,通常不考虑截面尺寸的影响,而将这些误差全部转化为混凝土容重的变化[3-4]。主梁混凝土容重的变化对成桥状态主梁线形、斜拉索索力、主梁应力的影响见图3~图5。
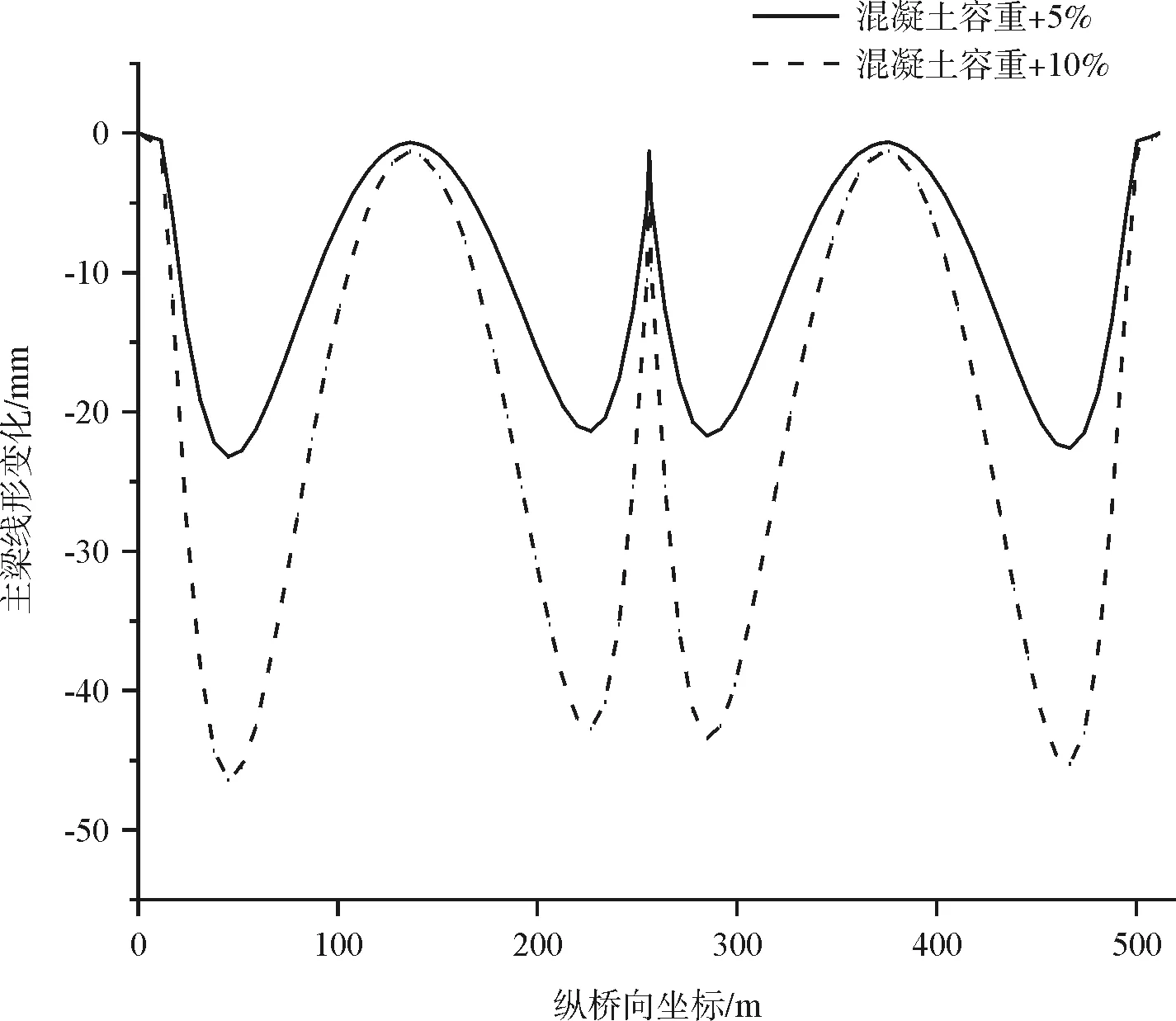
图3 混凝土容重变化时主梁线形变化

图4 混凝土容重变化时斜拉索索力变化

图5 混凝土容重变化时主梁应力变化
从图3~图5可以看出:主梁线形变化较大,最大绝对值为46.41 mm,位于边跨1/3位置,中跨跨中附近主梁线形变化也较大;斜拉索索力变化较大的是第4~6对斜拉索,最大绝对值为298.85 kN,远离桥塔的斜拉索索力变化相对较小;主梁应力变化最大绝对值为2.73 MPa,位于桥塔附近,中跨跨中处主梁应力变化较小。
2.2 主梁预应力荷载
在张拉主梁预应力钢束时,预应力的大小受张拉设备、锚固设备、管道的摩擦力以及预应力筋弹性模量等因素的影响,因此其大小与设计值往往存在偏差[5]。主梁预应力荷载的变化对成桥状态主梁线形、斜拉索索力、主梁应力的影响见图6~图8。

图6 预应力荷载变化时主梁线形变化
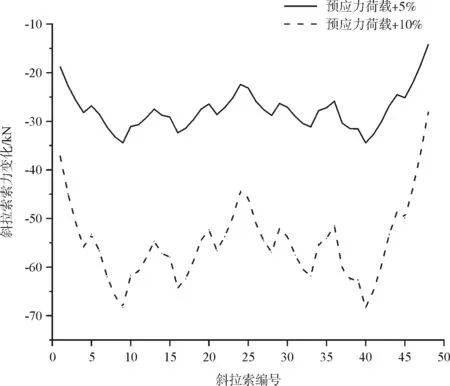
图7 预应力荷载变化时斜拉索索力变化

图8 预应力荷载变化时主梁应力变化
从图6~图8可以看出:主梁线形变化最大绝对值为10.22 mm,位于中跨跨中附近,边跨1/3位置处主梁线形变化也较大;斜拉索索力变化最大绝对值为68.34 kN,为边跨最长索,远离桥塔的斜拉索索力变化相对较大;主梁应力变化最大绝对值为1.80 MPa,桥塔附近主梁上缘应力变化较大,中跨跨中及靠近过渡墩处主梁下缘应力变化较大。
2.3 主梁弹性模量
实际施工过程中混凝土的弹性模量通常与设计值存在偏差,主梁弹性模量的变化对成桥状态主梁线形、斜拉索索力、主梁应力的影响见图9~图11。
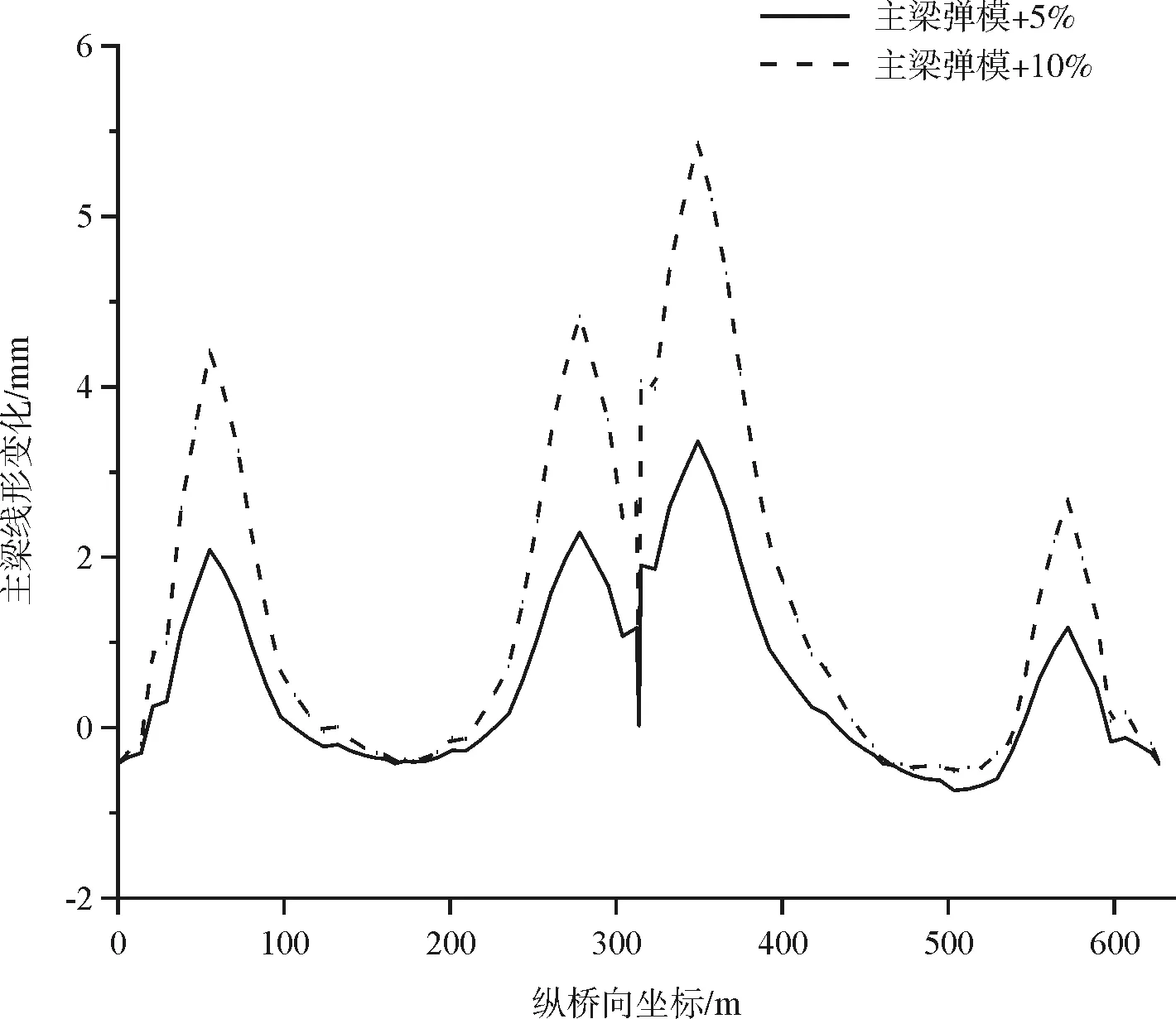
图9 主梁弹性模量变化时主梁线形变化
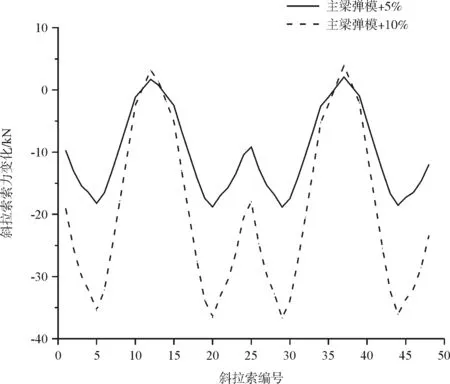
图10 主梁弹性模量变化时斜拉索索力变化

图11 主梁弹性模量变化时主梁应力变化
从图9~图11可以看出:主梁线形变化最大绝对值为6.93 mm,位于中跨跨中附近,边跨1/3位置处主梁线形变化也较大;斜拉索索力变化较大的是第7~9对斜拉索,最大绝对值为36.62 kN;主梁应力变化均较小,最大绝对值为0.2 MPa。
2.4 斜拉索弹性模量
实际施工过程中斜拉索的弹性模量一般也与设计值存在偏差,斜拉索弹性模量的变化对成桥状态主梁线形、斜拉索索力、主梁应力的影响见图12~图14。

图12 拉索弹性模量变化时主梁线形变化

图13 拉索弹性模量变化时斜拉索索力变化

图14 拉索弹性模量变化时主梁应力变化
从图12~图14可以看出:主梁线形变化较小,最大绝对值为3.45 mm,位于中跨跨中附近;斜拉索索力变化较大的是第7~9对斜拉索,最大绝对值为39.95 kN;主梁应力变化均较小,最大绝对值为0.13 MPa。
2.5 各控制目标的参数敏感程度分析
综合上述各结构参数的敏感性分析结果,将各参数变化引起的各控制目标变化量最大绝对值汇总,其结果见表2。
从表2可以看出:对成桥状态主梁线形、斜拉索索力、主梁应力影响最大的参数均为主梁混凝土容重。主梁混凝土容重、预应力荷载对各控制目标影响较大,为主要敏感性参数;主梁弹性模量、斜拉索弹性模量对各控制目标影响较小,为次要敏感性参数。
3 结论
本文以某矮塔斜拉桥为研究对象,以成桥状态主梁线形、斜拉索索力、主梁应力等结构静力响应为控制目标,对主梁混凝土容重、主梁弹性模量、斜拉索弹性模量、主梁预应力荷载等结构参数进行了敏感性分析,结果表明:
(1)对于成桥状态主梁线形、斜拉索索力、主梁应力等结构静力响应,主梁混凝土容重、预应力荷载为主要敏感性参数,主梁弹性模量、斜拉索弹性模量为次要敏感性参数。
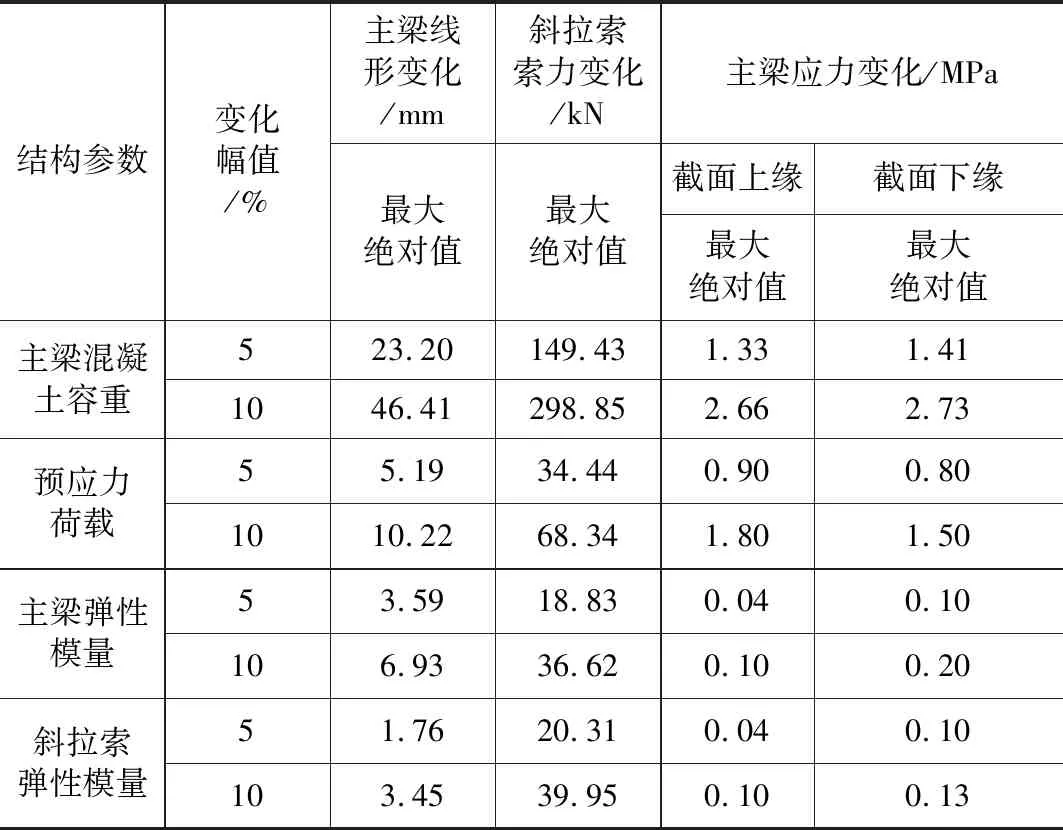
表2 结构参数变化引起的各控制目标最大变化量
(2)在施工控制中,需严格控制主梁混凝土容重,尽量减小混凝土超方、模板变形导致的截面尺寸误差,严格控制主梁预应力钢束的张拉,减小实测值与设计值之间的偏差。
(3)本文桥梁结构参数敏感性分析结果可为该桥的计算模型优化及误差调整提供依据,同时也可为同类桥梁施工控制提供参考。
