城市滑坡灾害生态风险不确定性分析及风险管理——以深圳市为例

吴健生,罗宇航,王小玉,赵宇豪,2

1 北京大学城市规划与设计学院, 城市人居环境科学与技术重点实验室, 深圳 518055 2 北京大学城市与环境学院, 地表过程分析与模拟教育部重点实验室, 北京 100871

随着城市化进程加快,城市生态系统与人类建设活动之间的矛盾日益凸显,引起了人们的广泛关注[1- 2]。城市的快速兴起加快了土地利用转化的进程,加剧了洪涝干旱、滑坡等灾害的发生[3- 5],生态风险不断增高,对人类生存发展和生态系统健康构成巨大威胁。生态风险是生态系统暴露在某种危险环境下遭受胁迫的可能性,具体是指种群、生态系统受到外界因素干扰时,结构、功能难以继续维持,其内部要素或其自身健康、生产力、经济价值和美学价值受损的概率[6]。目前,生态风险的研究多集中于评价人类活动造成的环境风险,如景观破碎化[7]、生态系统服务减少[8]和湖泊富营养化[9]等,以揭示生态风险分布情况。滑坡灾害生态风险作为常见的自然灾害生态风险类型,关注滑坡灾害对生态系统及其组分可能产生的不利影响。目前,其评价研究主要考虑滑坡灾害发生的概率、遭受滑坡影响时的敏感反应大小及受体遭受冲击时的潜在损失三类因素[10]。开展滑坡灾害生态风险评价对梳理定位高风险区域、防范风险不利后果具有重要意义。然而,有关评价本身多关注风险分级结果,缺乏明确的风险管理目标,导致具体措施难以实施。因此,考虑评价终点受到胁迫产生的不利效应后,还应提出相应的风险管理措施,从而为决策提供支持[11]。基于生态风险结构的滑坡灾害生态风险管理是一种客观的区域管理划分手段,能够根据风险评价结果提出相应的治理措施[10],但该方法在风险结构可视化方面较为薄弱,不利于城市风险分区管理,需要对其进一步改进。

此外,生态风险评价采用的数据、方法、信息的不完整,导致评价结果具有不确定性[6]。认识生态风险评价中不确定性的产生和传播机理,了解评价结果不确定差异,有助于明晰评价结果的准确性,合理管控生态风险。目前,针对生态风险不确定性的研究方法大致分为解析法和试验法[12- 13]两类。解析法运用概率论推算结果的不确定性,适用于服从统计分布的不确定性分析；试验法通过生成随机样本、建立公式联系、统计预测数据来分析不确定性,在剖析复杂计算过程的不确定性成因方面更具优势[14]。本文利用试验法——蒙特卡洛模拟分析误差产生和传播过程[14],从而计算特定评价流程产生的不确定性差异[6]。

深圳市是我国重要的窗口城市,自从1980年成为经济特区之后,城市化发展迅速,仅1996年到2015年,建成面积增长77.8%,且地处丘陵、低山、高台地地区,随着建设活动密度加剧,形成了众多不稳定边坡,在强降雨下极易诱发崩塌或大面积滑坡,造成生态破坏[11,15],因此,了解人类活动下的深圳市滑坡灾害危险分布、准确评价滑坡灾害下的潜在生态风险、提出合理的风险管理措施十分必要。本文利用“危险性-脆弱性-潜在损失”的三维评价框架[10],评价街道尺度下的生态风险,分析生态风险不确定性来源和传播过程,以准确认识不同评价单元的不确定性差异并希望揭示深圳市生态风险的风险结构特征,提出相应风险管理措施。

1 研究区与数据

1.1 研究区概况

深圳市(22°27′—22°52′N, 113°46′—114°37′E)位于我国广东省南部,北回归线以南,属亚热带季风气候,年均降雨1933.3 mm。截至2015年,全市下辖10个区,57个街道(图1),土地总面积1996.9km2,全市东西宽,中间窄,呈哑铃形,地势东高西低,最高海拔超过900米,地貌类型为低山、丘陵、台地、阶地和平原。低山和高丘陵占地17.95%,低丘陵占30.94%,台地及二级阶地占23.11%,平原及一级阶地占26.45%,其余为陆地水面。

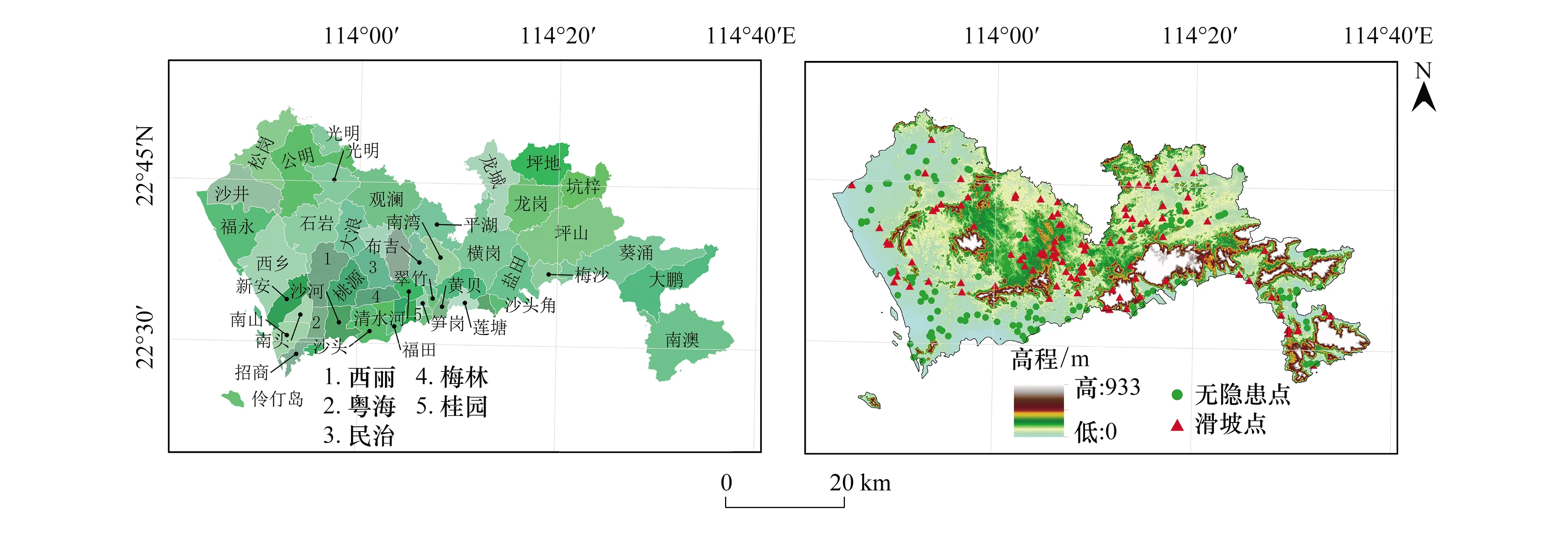
图1 深圳市街道及滑坡编录Fig.1 Subdistrict and landslide inventory of Shenzhen City

1.2 数据来源

本文基于深圳市政府2015年土地变更调查数据,参考《土地利用现状分类(GB/T 21010—2017)》,按研究需要重分类分为耕地、林地、草地、园地、水域、主要道路、独立工矿用地、铁路和其他建设用地九种用地类型。深圳市1∶5万地质图来自深圳市地质学会,对其进行空间校准和矢量化处理。DEM和Landsat TM影像数据为30 m分辨率栅格,来源于地理空间数据云(http://www.gscloud.cn/),用于生成坡度、坡面曲率和NDVI数据。降雨数据(2005—2015年逐日降雨量)来源于深圳市气象局，通过对全市54个气象观测点进行克里金插值得到多年平均降雨量。深圳市边坡数据点来源于深圳市规划和国土资源委员会的《深圳市边坡普查总结报告》。2008—2014年滑坡灾害数据来源于深圳市规划和国土资源委员会,滑坡位置以文字形式列出,在Google Earth软件中生成112例滑坡数据点；等量“无隐患点”为坡度小于2°[16]并在深圳市地质灾害易发程度分区图[17]中被划为地质灾害不易发区的随机栅格点(图1)。

2 生态风险评价

生态风险评价是指对区域内一种或几种不确定的事故或灾害对生态系统结构及其功能可能产生的不利影响进行的评价[18]。本文借助“生态风险(Risk)=危险性(Hazard)×脆弱性(Vulnerability)×损失(Damage)”三维评价框架进行区域生态风险评价[10],选用滑坡灾害作为评价危险性的灾种,关注景观结构生态学特征在面对灾害时表现出的脆弱性,用生境质量核算潜在生态损失,三因子等权重相乘完成评价。

2.1 基于BP人工神经网络的滑坡灾害危险性评价

随着人工神经网络在各类研究中的兴起,BP(Back-propagation)网络由于其能依靠计算机自动学习样本,受到较少的人工干预且精确程度较高,在滑坡等地质灾害评价中广泛运用[19- 21]。BP神经网络是一种基于误差反向传播进行权值训练的多层前向网络,目前运用最广泛的3层BP神经网络由单个输入层、隐藏层和输出层组成。BP网络训练的主要目的是拟合适宜的激活函数,不断调整权重和阈值,使输出值与实际结果之间的均方误差MSE(Mean Squared Error)达到设定目标,得到可用于预测的网络。

(1)

式中,K为网络测试集的样本数,ok为测试集的观测值,pk为神经网络的预测值。

利用深圳市112例历史滑坡点(设为“1”)和等量的“无隐患点”(设为“0”)共224例样本点对深圳市全域内的滑坡灾害危险性进行预测。随后提取样本点对应的环境因子,用于人工神经网络的训练和测试。考虑滑坡机理[15],本文从数据源中获取了9项环境因子,包括：高程、坡度、剖面曲率、平面曲率、地层岩性、断层距离、NDVI、边坡点核密度和年平均降雨量,将所有图层输出为60 m×60 m的栅格大小。为避免相似因素被重复考虑,导致模型估计失真,需识别环境因子之间的关联关系,剔除相关性较强的环境因子。利用波段集统计各图层的相关关系,发现高程和坡度相关关系中等,其余因子相关系数小于0.5,考虑到高程、坡度对滑坡发生的机理不一致,故不剔除,选用这9项因子评价滑坡灾害危险性(图2)。在环境因子选择上,剖面曲率和平面曲率控制着滑坡体的重量,两边坡同等剪切面下,凹形边坡的重量比凸形边坡更轻,凹形边坡比凸形边坡更难发生滑坡灾害；断层控制着岩层的破碎化程度,离断层越近,岩石更加破碎,降雨情况下易渗水失稳；边坡点核密度和NVDI在反应了人类活动的强弱,一定程度上可表征对地质环境的破环。其余因子都是文献中常用到的滑坡灾害危险性评价因子[15,22- 23]。

图2 深圳市滑坡灾害环境因子Fig.2 Environmental factors of landslide and collapse in Shenzhen

将9项环境因子极差标准化到[0,1]之间以消除量纲对结果的影响[22],提取224例样本点和深圳市546910个栅格点(60 m×60 m)的9项环境因子,在MATLAB R2014a中使用动量梯度下降法[21]训练人工神经网络并预测结果。为了检验滑坡评价的准确性,将样本点分为训练样本和测试样本两部分,分别占80%和20%。通过比对节点层数目,构建隐含层节点数目为16的前向网络,采用动量梯度下降法训练神经网络,设定误差目标为0.1,学习效率为0.02[21],网络在2545次迭代后达到训练误差目标0.1。将9个图层输入训练得到的BP网络中进行深圳市全域滑坡灾害危险性的预测,预测结果用测试样本和SPSS 22.0的ROC曲线进行检验并极差标准化到[0,1]后,导入ArcGIS中转为栅格数据进行分区统计,得到街道尺度滑坡灾害危险性。

2.2 生态系统脆弱性评价

生态系统脆弱性是指生态系统由于结构、组成不同,在面对外界干扰时产生的敏感反应大小,反映生态系统内部的不稳定性和在遭受干扰时的不可恢复性。生态系统脆弱性的定量表达方法和手段多样,如基于土地利用变化[24]、生态足迹[25]和景观格局指数等[26]。景观格局指数能定量解释景观异质性与生态过程的互馈关系,适宜于较大空间尺度的脆弱性刻画[26]。以深圳57个行政街道为基本评价单元,基于景观指数的生态学含义,考虑指数间的相关性,参考景观指数选择的技术、方法[10],综合脆弱性指数计算公式[27]如下：

(2)

式中,S为综合脆弱性指数,SHDI(香农多样性指数,Shannon′s Diversity Index)反映了生态系统的多样性、复杂程度,该指数越高生态系统越稳定。PD(斑块密度,Patch Density)表示景观的破碎程度,破碎度越高,空间异质性越高,生态系统抵抗外界干扰的能力越薄弱。DIVISION(景观分离度,Landscape Division Index)表示生态系统各组分的分离程度,分离程度越大稳定性越差。PAFRAC(周长面积比分维数,Perimeter-area Fractal Dimension)反映生态系统各组分的形状复杂程度,几何形状越复杂,生态系统越稳定。按照街道名称将街道矢量分裂为57个单独矢量文件并批量掩模土地利用栅格,将57个掩模栅格文件输入Fragstats 4.2中进行分析得到每个街道的四个景观指数,利用公式(2)计算得到街道尺度的综合脆弱性指数并极差标准化到[0,1]。

2.3 基于生境质量的潜在生态损失

滑坡灾害威胁着人员的生命财产安全,也威胁生物物种的续存。滑坡破坏地表植被并形成不稳定“创面”,阻碍物种迁徙,限制物种活动空间,其带来的砂土无法短时期沉降,从而造成水质降低,扰乱物种生存环境。生境的损失可以作为生态风险对物种影响的重要评价依据。

生境质量损失是本次风险因果链模型的“生态终点”,即评价生态系统在遭受滑坡灾害干扰和胁迫后在未来一段时间内表现出的状态。生境质量评价考虑人类活动对自然生境的影响,利用InVEST模型对2015年深圳生境质量进行评价,通过土地覆被图及威胁源对生物多样性威胁程度计算。InVEST模型的生境质量评价考虑四个因素：威胁源与生境之间的距离、不同生境对威胁源的敏感程度、生境受保护的水平和每种威胁的相对影响[28]。本文将草地、耕地、水域、园地和林地作为物种生境,主要公路、其他建设用地、独立工矿用地、铁路作为威胁源[29],设置权重和最大影响范围(表1),评价生境质量。生境质量结果0—1对应潜在生态损失从低到高,之后按街道单元分区统计潜在生态损失平均值,评价街道尺度潜在生态损失。

表1 威胁数据

2.4 生态风险管理

滑坡灾害生态风险防范分区是生态风险管理的重要举措,基于生态风险等级和生态风险结构,对高风险区域提出针对性的风险管控措施,为生态风险防范提供指导和参考[11,30]。运用“三基色”原理,考虑高风险区域三种结构因子中两种突出因子进行滑坡灾害生态风险管理分区。先将三项因子相乘得到的深圳市滑坡灾害生态风险数值按照自然间断法分为5个等级。同时,将滑坡灾害危险性通入红色波段,生态脆弱性通入绿色波段,潜在生态损失通入蓝色波段,“三基色”显示深圳市滑坡灾害生态风险结构。基于生态风险等级对深圳市57例街道进行滑坡灾害生态风险防范分区,生态风险等级较低区域可以自然适应发展,对于生态风险等级较高区域按照风险结构的主导因子进行分区防范,如品红色区域,由危险性和潜在损失共同主导,划分为一类区域。

本文认为滑坡灾害危险性较高的区域应当监测预警,脆弱性较高的区域应当给予保护,潜在生态损失比较高的区域应当避免人为活动,按照此规则将深圳市生态风险分为五区进行防范,具体防范如下：(1)自然适应调控区：区域风险等级整体较低,主导因素不明显,可视为风险防范的冷点,主要依托城市生态系统自身恢复和适应能力抵御在灾害,这些区域通常不易发生地质灾害,脆弱性、潜在损失较低；(2)避让保护兼顾区：生态脆弱性高、发生灾害后损失较高,建议避免剧烈的人为活动,保护自然环境；(3)避让监测预警区：滑坡灾害危险性高、发生灾害后损失较高,提议积极监测滑坡灾害、积极支护危险边坡,同时避免人为活动造成地质环境和物种生境破坏；(4)监测保护恢复区：滑坡灾害危险性高、生态脆弱性高,应该最大程度避免人为活动对山体稳定性的影响,维护景观的整体性；(5)综合风险管理区：整体风险较高,风险结构平衡,倡导综合滑坡灾害监测、生态环境保护、建筑活动避让的风险管理。

3 蒙特卡洛模拟分析生态风险不确定性

滑坡灾害生态风险评价中滑坡灾害危险性评价由于难以预测滑坡灾害准确的时间、地点和范围,结果往往具有较大的不确定性[12]。运用Excel插件Oracle Crystal ball(水晶球),采用蒙特卡洛方法(Monte Carlo method)进行“危险性-脆弱性-潜在损失”评价框架下的不确定性分析。

蒙特卡洛模拟是依靠随机数生成样本解决问题的方法,其核心思想是描述、构造概率模型并将问题转化为随机过程,而后从概率模型中抽取样本,统计结果的各估计量。对风险源栅格双线性重采样至1 km×1 km并转为栅格点,“标识”每个栅格点所属街道。在Excel中计算每个街道的栅格点的平均值,近似得到每个街道风险源的大小并乘以“源外”因子(脆弱性与潜在损失乘积)得到每个街道的生态风险。完成所有街道的风险计算后,利用Crystal ball进行蒙特卡洛分析。

社会和自然科学中事物大都服从或近似服从正态分布或半正态分布,运用正态云模型构建不确定性概率模型。本文仅在隶属度层次上定量探究生态风险的不确定性,不考虑其定性分级部分。正态云模型运用期望(Ex)、熵(En)和超熵(He)三个因子进行构建[13],具体为：假设A是精确数值量的集合A={x},称为论域。对于论域A上的任意数值量都存在一个稳定倾向的随机数,称x对A的隶属度,隶属度在论域上的分布为隶属云。论域A中x满足μx—N(Ex,En′2),其中En′—N(En,He2),隶属函数μ(x)满足：

(3)

则论域A的分布为正态云。正态云模型在正态分布中加入了超熵He(Hyper entropy)来描述熵的不确定性,它由熵的随机性和模糊性一同决定。He在隶属度图像上表现为云的厚度,云越厚,熵的不确定性越大。

在Crystal ball中,“定义假设”中设置生态风险源期望(Ex)为栅格点数值,熵(En)和超熵(He)分别为0.01、0.001[13]；“定义预测”设为街道生态风险源、生态风险的单元格；设置实验次数为1000次。模拟结束后提取模拟数据的不确定性(标准差),在SPSS 22.0中分析风险源不确定性与评价面积、生态风险不确定性与“源外”因子大小的回归模型。另外,将两因子极差标准化并同时加入生态风险评价不确定性模型中,诊断风险不确定性对评价面积、“源外”因子大小两个因素的敏感性。

4 结果分析

4.1 滑坡灾害生态风险空间特征

“危险性-脆弱性-潜在损失”评价框架包含滑坡灾害危险性、生态脆弱性、潜在生态损失三项因子。危险性结果的ROC曲线下面积AUC值为0.926,表明预测结果可信度较高,可以作为滑坡灾害评价结果。将三项环境因子数值按照自然间断法分为5个等级显示(图3)。结果表明：深圳市滑坡灾害危险性普遍处于相对较高水平,滑坡灾害危险区域集中在深圳中西部和东南部,西北部生态脆弱性较高,潜在生态损失从西到东呈现“低-高-低-高”交错分布。

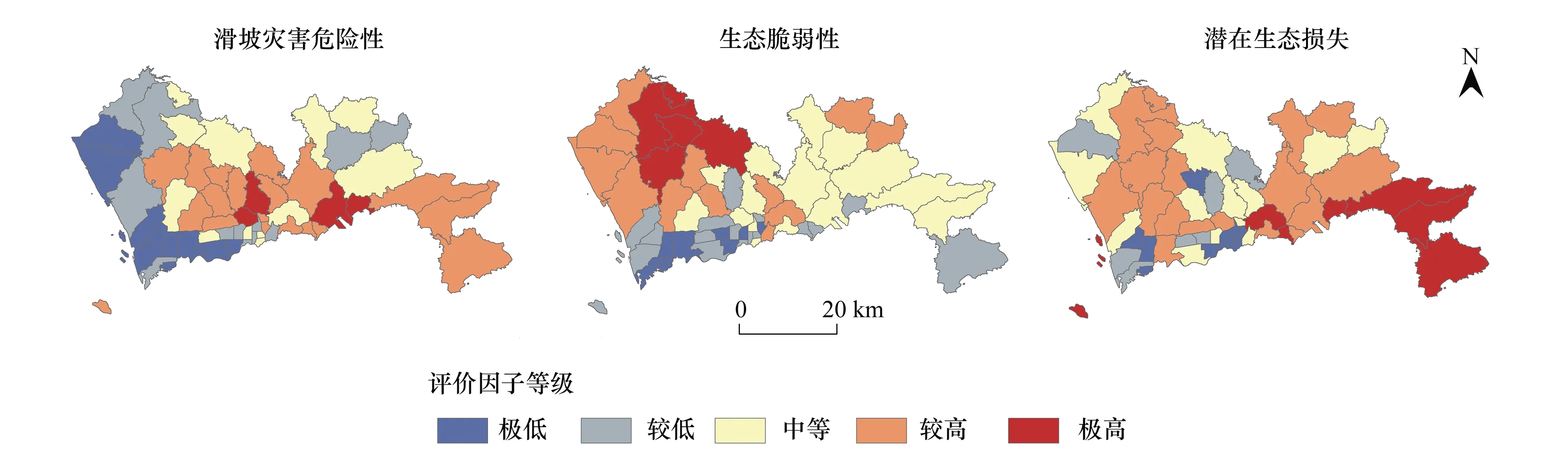
图3 滑坡灾害生态风险评价因子Fig.3 Ecological risk assessment factors of landslide disaster

图4 滑坡灾害生态风险等级Fig.4 Ecological risk level of landslide disaster

三因子等权重相乘获得深圳市滑坡灾害生态风险结果,按照自然间断法分为5个等级(图4)。结果表明：深圳市滑坡灾害生态风险从西到东呈现“低-高-低-高”的交错结构,深圳湾沿岸滑坡灾害生态风险较低,区域内建设用地集聚,生态用地较少,地势平坦,不具备孕灾条件；西北部和东南部滑坡灾害生态风险较高,区域内植被覆盖良好,潜在生态损失较高。

“三基色”显示深圳市滑坡灾害生态风险结构(图5),运用“三基色”原理分析生态风险结构[31],结果表明：西北部和东南部滑坡灾害生态风险结构呈现空间集聚特征,中西部风险结构分异明显。深圳市西北侧风险结构从北到南呈现青色-暗粉色-紫灰色,表明滑坡灾害危险性上升、生态脆弱性降低、潜在生态损失恒高的特征；中部及东部风险结构由西向东为灰紫色、品红色,表明生态脆弱性较低,滑坡灾害危险性、潜在生态损失较高；西部沿江和深圳湾沿岸的生态风险不高,风险结构图上为较暗的青色、蓝色和红色。西部沿江-深圳西北侧有显著明暗边界,边界上滑坡灾害生态风险变化明显。“三基色”显示全市主要的风险结构为“高危险-高潜在损失”型的品红色和“高脆弱-高潜在损失”型的青色。

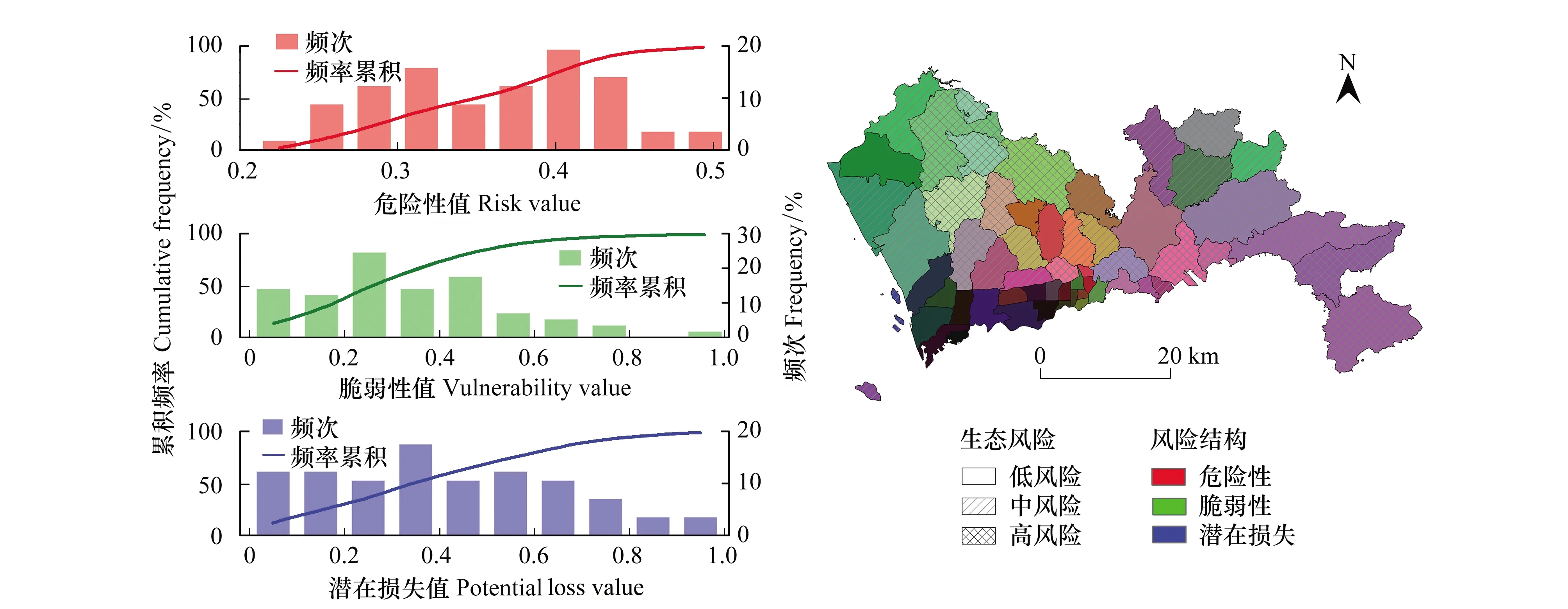
图5 滑坡灾害生态风险结构Fig.5 Ecological risk structure of landslide disaster

4.2 不确定性分析结果及机制探讨

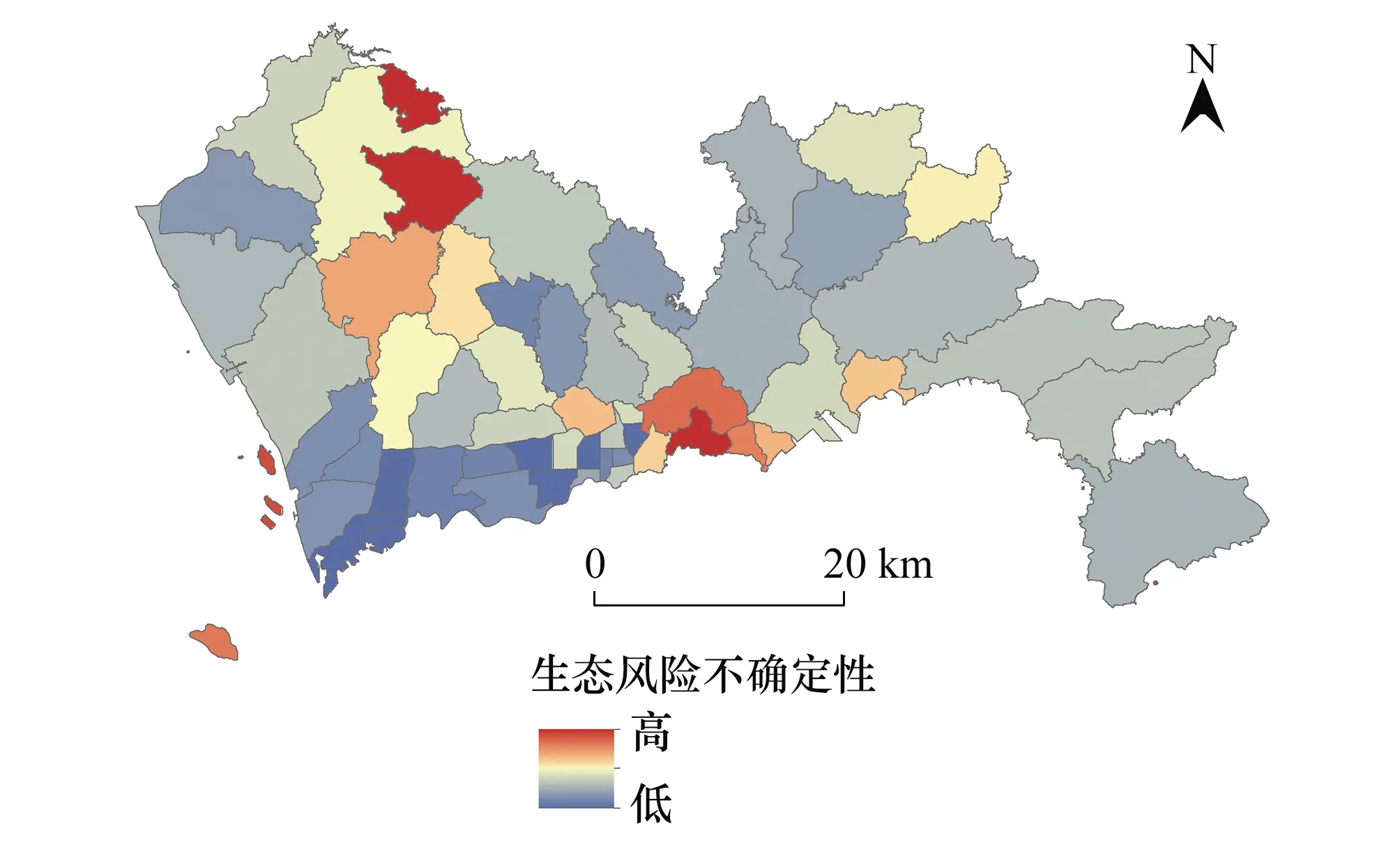
图6 生态风险不确定性Fig.6 Ecological risk uncertainty

蒙特卡洛模拟得到深圳市滑坡灾害生态风险不确定性(图6)。结果表明：滑坡灾害生态风险评价值不确定性普遍处于相对较低水平,评价结果整体可信度较高；深圳市西北侧、梧桐山、内伶仃岛及附近岛屿风险评价值的不确定性相对较高,这些区域评价结果可信度相对较低。定量评价生态风险不确定性,分析评价单元不确定性差异,有助于了解评价结果有效性的空间差异。

探究生态风险不确定性与街道斑块面积的回归关系(图7a)。结果表明：当风险源与面积之间的关系设置为幂函数的时候解释程度最佳(R2=0.983,P<0.001),模型为：

y=0.01x-0.506

(4)

式中y为生态风险源不确定性,x为评价面积(km2)。模型表明生态风险源不确定性将随着面积的增加而增加,也就是在同一套数据下,面积越大的街道,生态风险源的不确定性越高,但随着评价面积的不断增加,风险源不确定性的减小程度明显降低。

图7 不确定性来源及传播过程Fig.7 Uncertainty source and transmission process of the ecological risk

“危险性-脆弱性-潜在损失”评价框架下,“源外”因子为“脆弱性”与“潜在损失”之积,生态风险源的不确定性将经过“源外”因子传播到生态风险评价结果中,影响评价结果的不确定性。研究发现滑坡灾害生态风险不确定性与“源外因子”大小之间存在着显著的正相关关系(图7),即“高脆弱性-高潜在损失”的街道,滑坡灾害生态风险评价值的不确定性较高,而“低脆弱性-低潜在损失”的街道,评价值的不确定性较低,模型为：

y=0.001173x+0.010

(5)

式中y为生态风险值不确定性,x为“源外”因子大小,模型的t统计量、F统计量在0.05的显著性水平下通过检验,R2为0.509。

不确定性对评价面积、“源外”因子大小两个因素的敏感性的诊断结果如下：

y=0.001180x1-0.000505x2+0.000148

(6)

式中y为生态风险不确定性,x1为“源外”因子大小,x2为评价面积。模型通过显著性检验,R2为0.753。结果表明：从不确定性产生到影响评价结果,“源外”因子大小占据着主导因素,其敏感性约为评价面积的2.3倍。风险源不确定性在经过“源外”因子传播的时候被“放大缩小”,这一部分原因需要在生态风险评价中着重考虑。

4.3 滑坡灾害生态风险防范分区

对风险防范划分区域进行统计,结果表明:避让保护兼顾区、综合风险管理区、避让监测预警区、监测保护恢复区和自然适应调控区的街道总数比例分别为14.04%、1.76%、29.82%、5.26%和49.12%,街道总面积比例分别为29.31%、2.68%、41.73%、4.25%和22.03%(图8)。避让保护兼顾区分布于深圳西北部光明区及附近区域和东北部坑梓街道,避让监测预警区集中在深圳东部地区和羊台山-塘朗山沿线,监测保护恢复区位于布吉、民治、南湾街道,自然适应调控区位于西部沿江-深圳湾地区及北部部分地区。深圳西部风险防范类型较多,分异明显,需要做到精细化风险管理,东部风险防范类型比较单一。

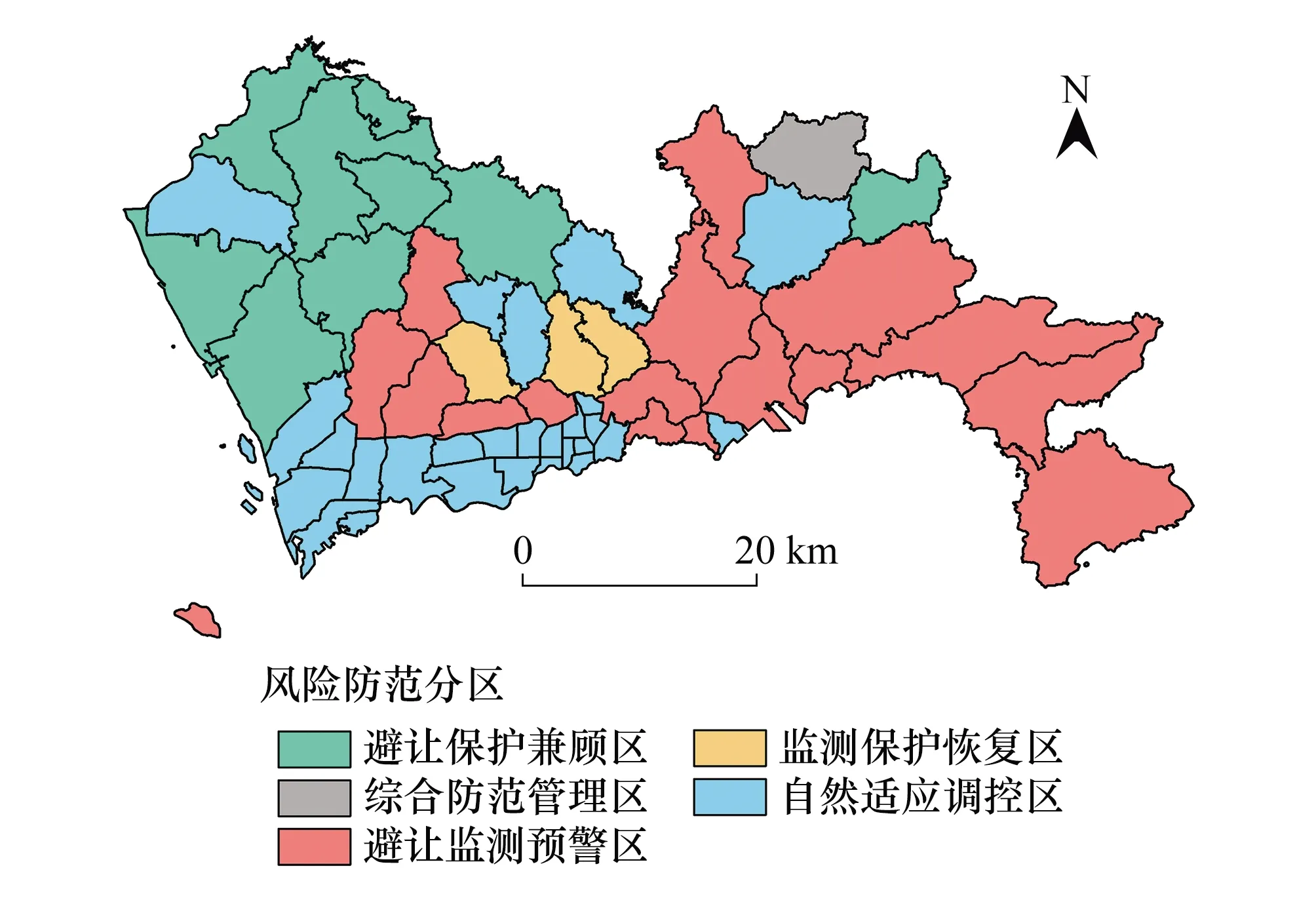
图8 滑坡灾害生态风险防范分区 Fig.8 Ecological risk prevention division of landslide and collapse

5 讨论

以往研究表明,评价面积越大,数据格点越多,不确定性越小,但目前很少有研究对此进行准确认识[6,32]。本文通过蒙特卡洛模拟和正态云模型,定量分析评价面积带来的不确定性差异,发现风险源不确定性与评价面积间呈显著负相关关系,随着评价面积的增加,不确定性减小程度变小。这一结论可被“中心极限定理”证明,即样本量越大,样本均值越“稳定”。

风险源不确定性的传播过程是复杂的,迫切需要认识传播过程如何影响生态风险评价[14]。研究表明,“源外”因子大小是导致风险值不确定的敏感因素,其影响远大于评价面积差异带来的影响。“源外”因子大小缩放风险源不确定性,导致评价值不确定性成倍数出现差异,在对风险值分级时,“源外”因子较大的街道错分概率更大。

生态风险等级显示,深圳市东南部和西北部生态风险较高但风险结构各不相同,东南部风险结构为“高危险-高潜在损失”型,西北部风险结构为“高脆弱-高潜在损失”型,因此,需要制定不同的风险管理措施。在前人研究基础上[10],基于“三基色”原理分析生态风险结构,以此作为生态风险防范分区依据划定了五类防范区,实践效果良好,今后利用“三基色”原理分析结果的三维结构不失为一种简便方法。

本文研究方法也存在一些局限,包括：(1)用“标识”的方法确定街道边界栅格所属街道较为粗略；(2)构建概率模型时,设定所有栅格的不确定性相同；(3)分析不确定性时,仅仅在隶属度层次上考虑不确定性,未考虑不确定性风险等级划定后对结果的影响。今后应进一步考虑风险等级层面上的不确定性,完善生态风险不确定性的研究范式,为城市建设可持续发展提供理论和决策基础。

6 结论

(1)深圳滑坡灾害生态风险从西到东呈现“低-高-低-高”的交错结构。高滑坡灾害生态风险主要分布于深圳市西北侧和东南侧,风险结构为“高脆弱-高潜在损失”型和“高危险-高潜在损失”型,应分别采取避让保护和避让监测的管理措施。利用“三基色”原理,考虑高风险区域的主导因子,可实现生态风险的合理管控。

(2)随着评价面积增加,生态风险源不确定性减少。蒙特卡洛模拟定量分析风险源不确定性与评价单元面积的关系,发现其不确定性与评价面积呈显著的负相关关系,较大斑块的风险源不确定性较小,较小斑块的风险源不确定性较大。以风险源为不确定性主体生态风险评价中,面积越大的评价单元,生态风险源数值越“稳定”。

(3)以风险源为不确定性主体的生态风险评价中,“源外”因子越大的评价单元,生态风险值可信度越低,评价结果越容易失误。生态风险评价的不确定性由生态风险源不确定性和“源外”因子大小共同主导,“危险性-脆弱性-潜在损失”评价框架下,“脆弱性-潜在损失”为“源外”因子,其大小影响着风险源不确定性的传播过程,是生态风险评价不确定的敏感因素。