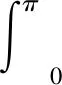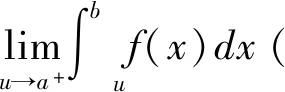一例经典瑕积分的计算方法探究

王成强

(成都师范学院 数学学院，四川 成都 611130)

瑕积分，即针对某些特殊无界函数定义的“反常”积分。大学数学的瑕积分理论是Riemann积分理论的延伸与有力补充，它为某些来自于物理等其他科学的本无Riemann积分的无界函数提供了定义积分的可能。瑕积分理论的学习能加深对Riemann积分、极限等理论的理解，为函数的Lebesgue积分理论的学习提供积累经验的机会。

要学好瑕积分理论，需要掌握好瑕积分相关的概念与性质，需要理解性地记忆好各类瑕积分的收敛判别条件，需要深刻理解并记忆几个特殊瑕积分的收敛性。本文的研究对象是：

一、预备知识

对指标变量做替换，可得

二、问题(*)的九种解法

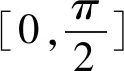
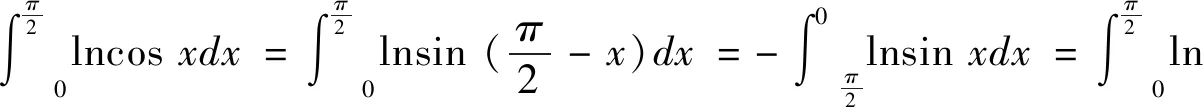
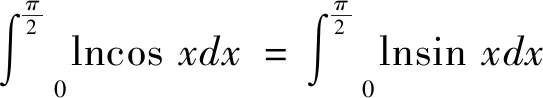
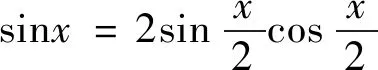
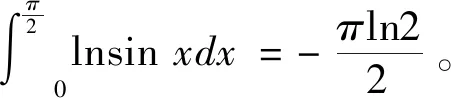
方法5经计算，有：

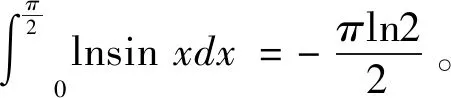
于是，

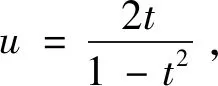
于是，

进而可得：

解得：

于是，

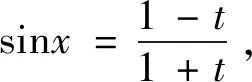
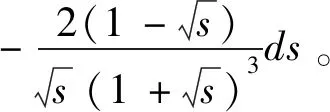
借助于该发现，按下述方式继续，

利用区间可加性，有

于是，

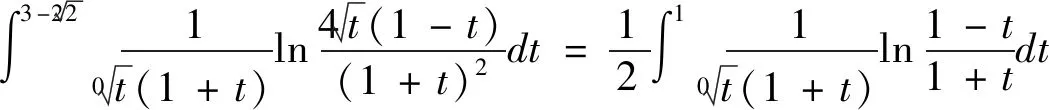
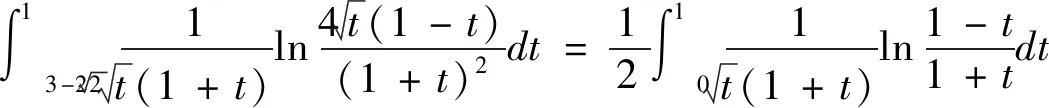
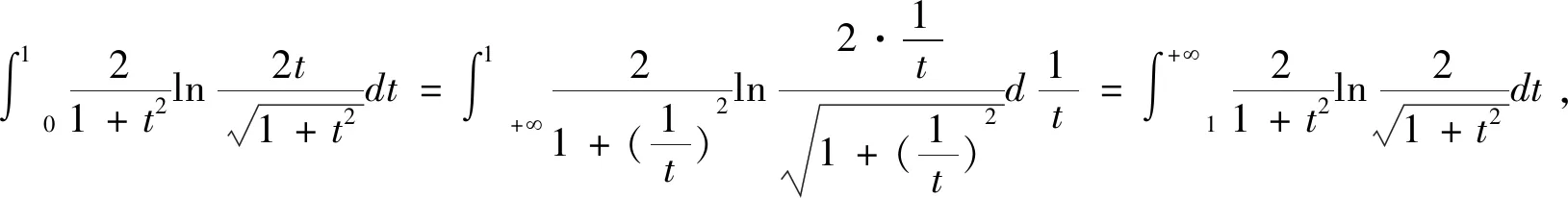
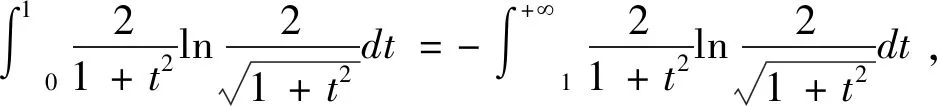
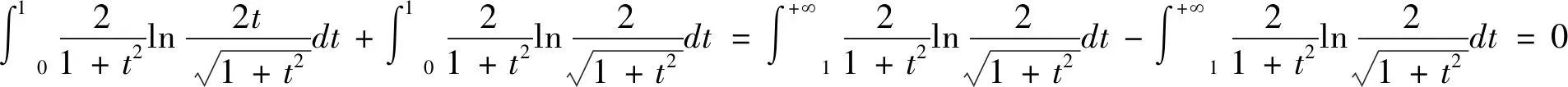
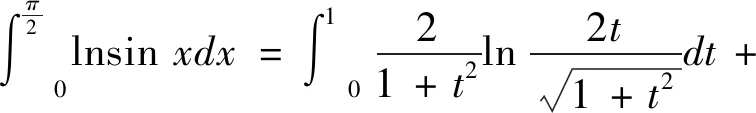
三、结语