基于GA-BP神经网络的隧道围岩力学参数反演

刘 军，翁贤杰，张龙生，张连震

(1. 山东大学 土建与水利学院，山东 济南 250061；2.江西省高速公路投资集团有限责任公司，江西 南昌 330025；3.江西交通咨询有限公司，江西 南昌 330008；4. 中国石油大学(华东) 储运与建筑工程学院，山东 青岛 266580)

0 引言

随着计算机技术的发展，数值分析理论和计算在岩土工程中得到进一步的推广和应用。虽然数值模拟计算中有着较合理的计算模型，但是数值模拟中的岩体力学参数却由于岩体的尺度效应、取样有限等难以确定合理的取值。为了解决这一问题，岩体力学参数反分析成了确定数值模拟计算参数的有效方式之一。戴薇等[1]利用支持向量机方法反演得到了围岩的侧压力系数，并通过正演分析进行了验证；万智勇等[2]通过均匀设计建立了BP神经网络的样本，并反演得到了坝基的力学参数值；王军祥等[3]运用基于粒子群优化的BP神经网络算法对围岩力学参数进行了反演，并分析了台阶法开挖时隧道的变形情况；周冠南等[4]采用基于遗传算法与BP神经网络相耦合的计算方法，提高了反演分析的效率；杨茜[5]采用对比优选网络训练模式和传递函数，改进了BP 神经网络方法，对隧道整体沉降进行了预测；赵杰[6]等运用有限元软件结合BP神经网络，对穿越粉质黏土层及砂卵石地层的地铁暗挖隧道进行了正演分析；吕志涛等[7]以隧道监控量测数据为依据，反演了隧道所在岩体的蠕变参数；饶云康等[8]根据收集的砾类数据样本，分别构建了基于GA-BP神经网络和标准BP神经网络的砾类土最大干密度预估模型，发现采用前者能较好地预估砾类土的最大干密度；张飞等[9]结合大岗山水电站洞室分层开挖的特点，利用GA-BP神经网络实现了施工期岩体参数的精细反演；盖宏健[10]结合单轮土槽试验，运用GA-BP神经网络预测了星壤的剪切和承压力学参数；李振涛等[11]利用正交设计、GA-BP神经网络，反演获得了较为精确的盾构扰动区砂土体力学参数；祝江林等[12]运用敏感性分析，获得了影响白水隧道围岩变形的主要力学参数，并通过GA-BP神经网络对围岩力学参数进行了反演；关永平等[13]利用GA-BP神经网络，结合均匀设计对绿春坝隧道围岩力学参数进行了反演。

本研究以江西省萍莲高速公路莲花隧道为依托工程，利用正交试验组合，结合有限差分法，构造了神经网络样本，并通过训练获得成熟的GA-BP神经网络模型。依据莲花隧道监控量测实测数据反演得到了隧道的围岩力学参数，并通过误差分析验证了参数反演结果的可靠性，这一方法可供隧道工程后续施工与设计使用。

1 工程概况

莲花隧道起点位于萍乡市湘东区，终点位于莲花县六市乡，莲花隧道为分离式隧道，左线总长3 210 m，右线总长3 220 m。隧道围岩分级为Ⅳ，Ⅴ，Ⅲ级围岩，其中Ⅳ级围岩占隧道总长的47.6%，Ⅴ级围岩占隧道总长的33.7%，Ⅲ级围岩占隧道总长的18.7%。隧道最大埋深317 m。

隧道区穿越华夏板块华南造山系之东南造山带的武功山-会稽山前缘褶冲带之武功山隆起，基底褶皱强烈，区内断裂带发育。隧道区地表常年有水，主要地下水为基岩节理裂隙水，主要接受大气补给降水。据现场工程地质调绘及钻孔资料分析,在钻孔揭露范围内隧址区地层结构自上面下依次为第四系粉质黏土及碎石土；青白口系库里组下段砂质板岩、泥盆系上统洋湖组砂岩、泥盆系上统麻山组钙质泥岩等。岩体较破碎至较完整，受地下水影响较大。

2 数值计算模型

2.1 数值模型

为保证数值计算的准确性，隧道计算模型的几何尺寸按照施工设计图纸建模。选取莲花隧道右洞进洞口某段作为施工模拟对象。该段平均埋深26 m，围岩等级为Ⅴ级。为避免模型边界过大，致使计算缓慢，根据相关文献[14-15]，隧道纵向长度取40 m，隧道的左右边界各取隧道洞径的3倍，隧道的下边界取3倍洞径；隧道的前边界、后边界、左边界、右边界以及模型的底部边界均施加法向约束，模型的上边界为自由边界。数值计算模型及网格划分情况如图1所示。

图1 计算模型及网格划分Fig.1 Calculation model and meshing

2.2 计算参数

数值模拟计算中，隧道围岩材料采用三维实体单元进行模拟。采用cable结构单元模拟超前小导管，长度取4 m，直径为42 mm，壁厚3.5 mm；利用shell结构单元来模拟初衬，厚为25 cm；二次衬砌采用实体单元来模拟，厚为55 cm。在材料本构属性方面，围岩材料采用莫尔—库伦模型，初衬以及二次衬砌则按弹性结构模型，隧道施工过程中的钢拱架、系统锚杆以及钢筋网片则利用适当提高喷射混凝土的弹性模量来模拟[16-17]。超前支护加固区域采用等效加固的效果模拟，其参数取值分别为：厚度取值1.0 m，按照弹性模量取值1.0 GPa，内摩擦角取值35°，黏聚力取值400 kPa。根据莲花隧道地质勘察报告、现行《公路隧道设计规范》，确定隧道围岩力学参数的取值范围，计算模型的力学参数如表1所示。

2.3 计算过程

对拟开挖区域赋予null属性实现，通过一定的时步，模拟隧道实际开挖过程中各工序滞后产生的应力释放。隧道采用微台阶法开挖，仰拱快速闭合。隧道的开挖进尺取1 m，各台阶长度均匀3 m，开挖到第16步时，按照第13～15步的顺序循环开挖，直至隧道仰拱向前掘进了10 m，选取距离掌子面5 m处的断面为隧道监测断面。隧道从上台阶开挖到初期支护封闭成环，其具体开挖工序如表2所示。

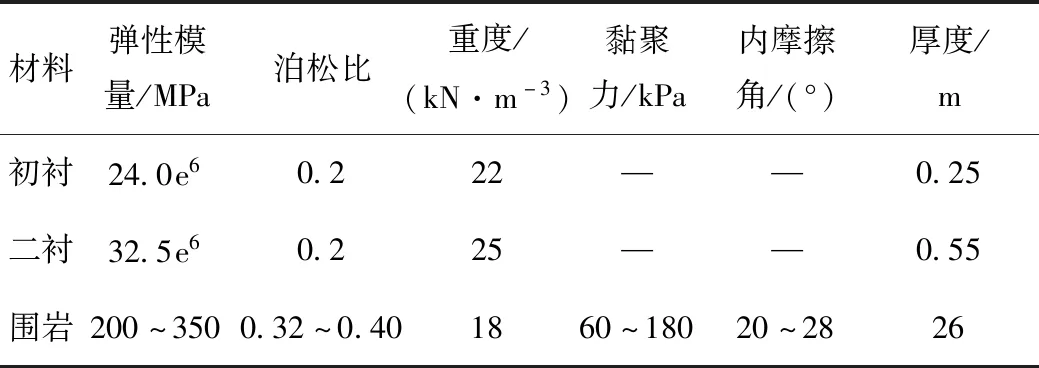
表1 围岩力学及支护参数Tab.1 Mechanical and support parameters of surrounding rock

表2 数值模拟隧道开挖支护过程Tab.2 Numerical simulation of tunnel excavation and support process

3 GA-BP神经网络围岩力学参数反演

3.1 BP神经网络

BP神经网络是采用误差反向传播计算的算法，有着良好的自组织学习能力，是目前应用最为广泛的神经网络模型之一。BP神经网络包括输入层、隐含层、输出层，它能够实现从输入到输出的任意非线性映射[18-19]。

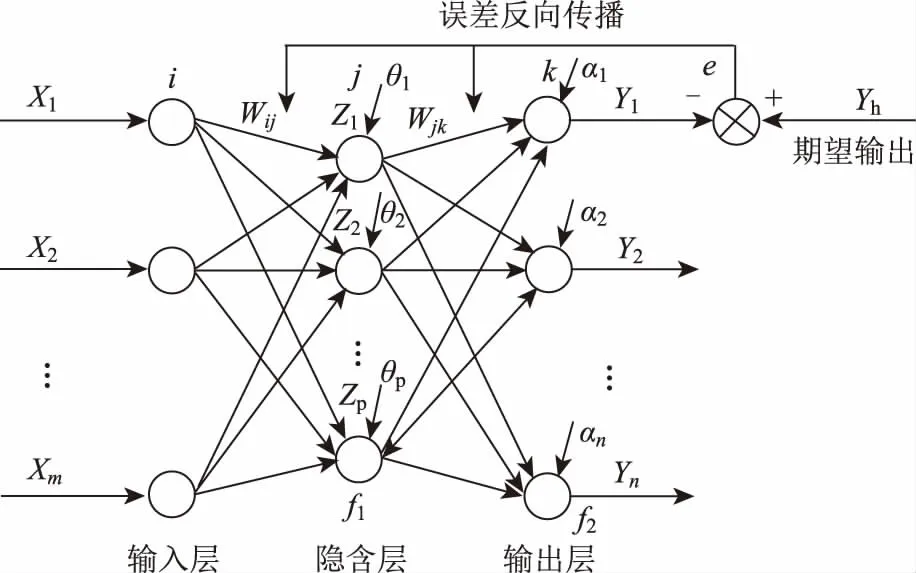
图2 BP神经网络结构Fig.2 BP neural network structure

如图2所示，输入层神经元有m个，隐含层有p个，输出层有n个。输入层到隐含层的权值为Wij(i=1,2,…,m;j=1,2,…,p)，隐含层到输出层的权值为Wjk(j=1,2,…,p;k=1,2,…,n)，隐含层的阈值为θj(j=1, 2,…,p)，输出层的阈值为αk(k=1,2,…,n)。神经网络的输入向量为X1,X2,…，Xm，神经网络的输出向量为Y1,Y2,…，Ym,期望输出为Yh，神经网络期望输出值与实际输出值的误差e。在BP神经网络训练时，权值为随机值，输入学习样本得到网络的输出值，然后通过输出值与期望值的误差值，再通过修改网络参数，达到使误差值不断减小的目的，如此反复，直至误差值不再下降，就能得到训练成熟的神经网络模型。

本研究先基于经验公式确定隐含层神经元节点数取值范围，再利用控制变量法，通过改变隐含层神经元个数，建立多个不同的神经网络模型，以误差为指标。经过多次试算，从而确定神经网络的拓扑结构为3-6-3。

3.2 GA-BP神经网络

GA-BP神经网络通过优化BP神经网络中随机生成的初始权值与阈值，使得传统的BP神经网络具有更优的非线性映射能力，具有更好的预测能力。

图3 GA-BP算法流程图Fig.3 Flowchart of GA-BP algorithm

在GA-BP神经网络中，首先对种群个体进行编码；再利用神经网络训练误差并将此作为适应度函数；其次，通过选择、自适应交叉和变异算子，获得种群最佳适应度个体；最后将种群最佳适应度个体作为神经网络的最佳初始权值、阈值；继而代入到BP神经网络中进行训练、预测仿真，直到达到满足设定的预测误差要求或者达到设定的最大迭代次数结束，从而获得成熟的GA-BP神经网络。其算法流程如图3所示。

3.3 神经网络样本

为了建立成熟的GA-BP神经网络，必须通过一定数量的神经网络样本对神经网络进行学习，并对训练好的神经网络模型进行检验。为此，设计了25组力学参数的正交试验，按照建立的数值模型和开挖支护工序分组计算，获得相应的拱顶沉降、周边位移以及地表沉降值。

以每组正交试验计算得到的拱顶沉降、周边位移以及地表沉降[U1,U2,U3]作为输入向量，对应的黏聚力、内摩擦角、弹性模量、泊松比[c,ψ,E,μ]作为输出向量。得到GA-BP神经网络样本如表3所示。

3.4 数据归一化及网络模型参数设置

由于神经网络样本数据的量级相差较大，如果不进行处理，可能会导致神经网络计算时间长。因此，为保证训练效果，需要先对输入向量和输出向量分别进行归一化处理。利用最大值最小值法，采用MATLAB内置的mapminmax函数对样本进行归一化处理。将样本中的输入向量、输出向量归化到[0,1]区间，再利用MATLAB平台的BP神经网络对样本进行网络训练，并通过反归一化得到输出向量。

根据BP神经网络算法原理以及相关参数设置要求，隐含层的传递函数、输出层的传递函数选取为logsig函数，网络训练函数选取为改进的L-M算法，神经网络的学习速率η设定为0.05，网络的误差设定为0.01。在本次反分析中，根据控制变量法确定遗传算法控制参数，其中遗传算法种群规模取30；最大遗传代数取值25；交叉概率取值0.8，变异概率取值0.01。

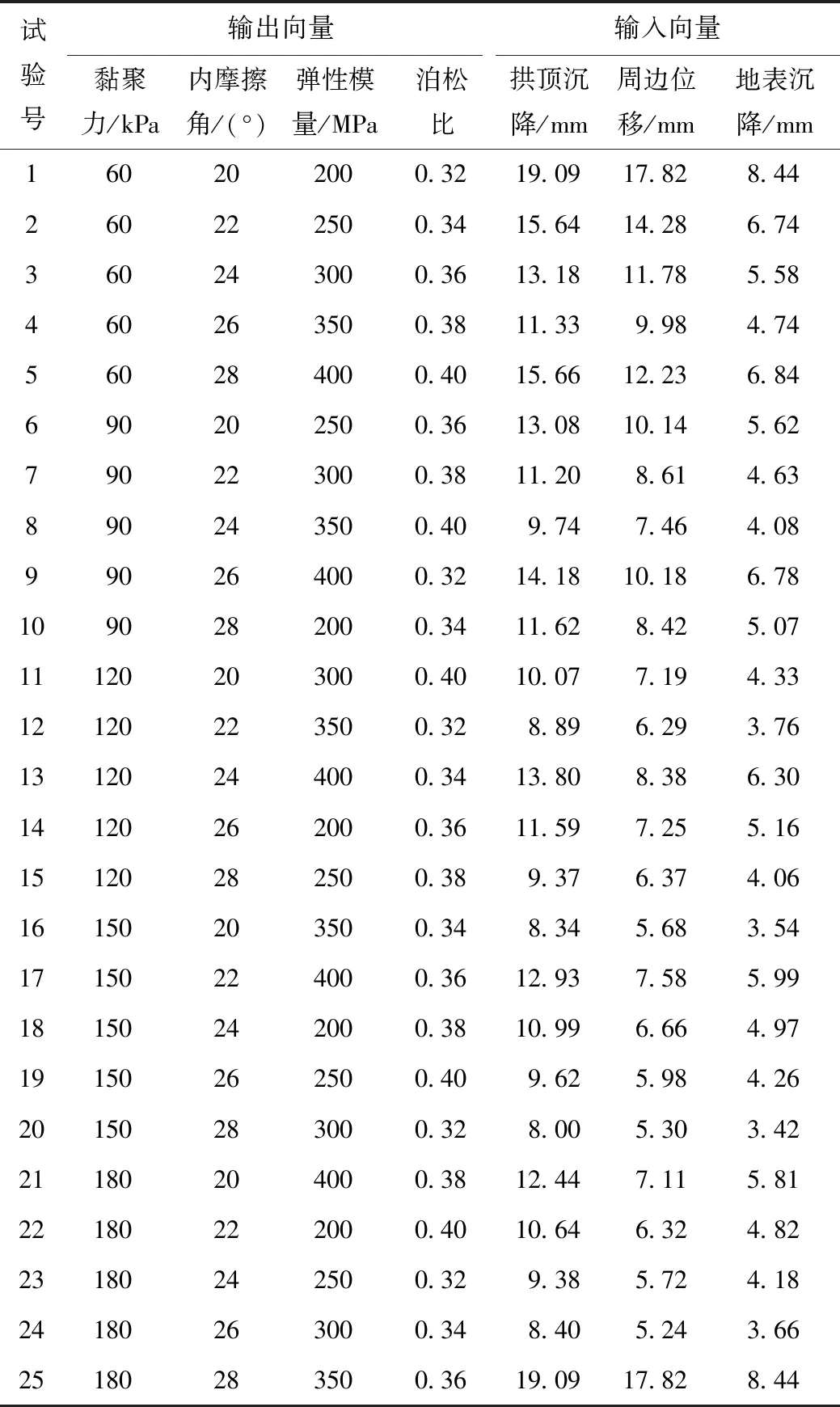
表3 GA-BP神经网络样本Tab.3 GA-BP neural network samples

利用表3的神经网络样本对GA-BP神经网络训练，得到训练成熟的GA-BP神经网络。将部分样本代入到训练好的神经网络中进行检测，对比分析预测值与期望值之间的误差，以此检测训练好的GA-BP神经网络的仿真预测能力是否能够达到要求。如果未达到要求，通过调整参数，迭代计算直至满足误差要求。

3.5 现场监控量测数据回归分析

调取莲花隧道进口右洞YK35+115断面的监控量测数据进行分析探讨，围岩实测变形情况如图4所示。利用最小二乘法对围岩的水平收敛、拱顶沉降及地表沉降位移监控量测数据进行回归分析：

地表沉降：y=-5.312e(-t/7.835)+5.02；

拱顶沉降：y=-11.050e(-t/4.588)+11.27；

周边收敛：y=-7.586e(-t/6.639)+7.22。

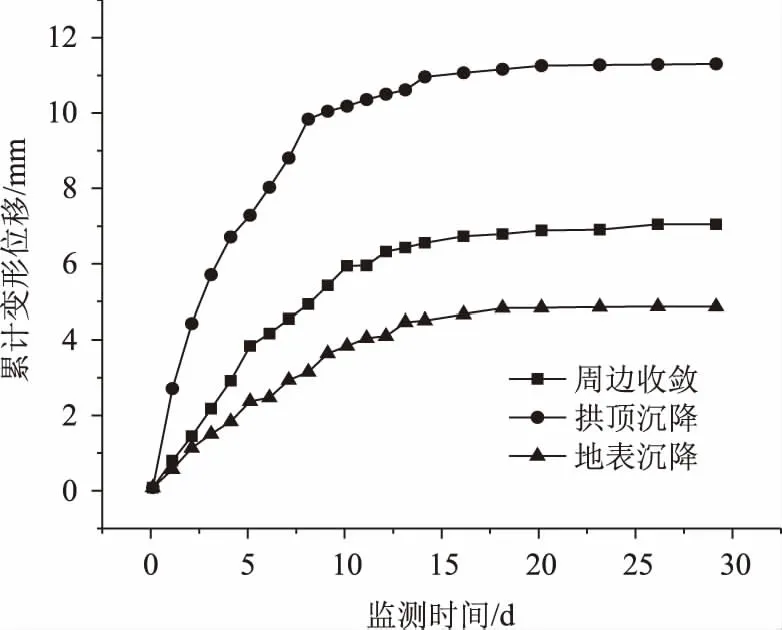
图4 隧道变形位移随时间变化曲线Fig.4 Curves of tunnel displacement vs. time

3.6 位移反分析计算结果

调取莲花隧道断面YK35+115的监控量测数据，把实测变形位移值[11.21；6.95；4.73]作为输入向量，代入到成熟的GA-BP神经网络中，得到围岩力学参数输出向量[118.64；26.42；212.35；0.36]。

为了验证参数反演结果的可靠性和准确性，再将输出的围岩力学参数值代入到上述建立好的FLAC3D模型中进行正演计算，得到莲花隧道的拱顶沉降、周边位移、地表沉降数值(如图5所示)，并与实测位移进行误差分析。隧道围岩力学参数反演计算结果及误差情况如表4所示。

图5 正演计算位移云图(单位：m)Fig.5 Nephograms of displacement by forward calculation(unit: m)

表4 隧道围岩力学参数反演计算及误差分析Tab.4 Inversion and error analysis of mechanical parameters of tunnel surrounding rock

分析表4可知，基于隧道YK35+11断面拱顶沉降11.21 mm；周边位移6.95 mm；地表沉降4.73 mm 的实测位移情况，通过GA-BP神经网络反演计算，得到隧道进洞口YK35+095～YK35+135段围岩的黏聚力118.46 kPa，内摩擦角26.42°，弹性模量212.35 MPa，泊松比0.36。根据反演得到的围岩力学参数，运用FLAC3D有限差分法计算，得到隧道拱顶沉降11.55 mm，与实测拱顶沉降相对误差2.94%；周边位移7.17 mm，与实测周边位移相对误差3.16%；地表沉降4.96 mm，与实测地表沉降相对误差4.86%；正演计算的各位移值与实测值相差很小。可见，采用GA-BP神经网络反演围岩力学参数方法准确度较高，对围岩变形预测较为接近。

4 结论

(1)应用GA-BP神经网络，对利用正交设计试验并结合有限差分法构造的样本集进行训练，得到了训练成熟的GA-BP神经网络，可以方便地反演计算围岩力学参数。

(2)采用GA-BP神经网络反演分析方法，得到围岩力学参数的误差较小，具有较高的精度和可靠性。莲花隧道右洞进口段反演得到的力学参数应用到FLAC3D中正演计算，得到拱顶沉降，周边位移和地表沉降与现场实测值仅相差2.94%，3.16%和4.86%，反演结果较为准确。可见，基于GA-BP神经网络的隧道围岩力学参数反演方法，可为隧道设计提供所需的计算参数，对隧道信息化动态设计及施工有一定的应用价值。