基于SVPWM永磁同步电机调速系统研究
2020-07-16赵斯博毕永利
赵斯博,毕永利,张 妍
(黑龙江大学 机电工程学院,哈尔滨 150080)
0 引 言
随着电力电子技术快速发展,以永磁同步电机为执行机构的伺服系统应用领域越来越广泛,涉及航空、机械、运输、轻工等多个行业[1- 4]。在信息时代下,对伺服系统提出智能化、快速性、准确性等更高要求,伺服驱动成了必不可少的关键技术。本文基于SVPWM对永磁同步电机调速系统进行研究,并在MATLAB/Simulink平台上进行验证。
1 交流永磁同步电机数学模型
永磁同步电机的工作原理是定子绕组在通电流时会产生磁动势和磁场,转子在电磁力作用进行同步旋转。永磁同步电机是一个多变量、非线性、强耦合的系统,为简化永磁同步电机的数学模型,做如下假设:①忽略电机铁心饱和;②忽略电机中涡流和磁滞损耗;③忽略磁场中空间谐波作用;④各相绕组对称[5-6]。
永磁同步电机电压方程:
(1)
转矩方程:
Te=p[ψfiq+(Ld-Lq)idiq]
(2)
运动方程:
(3)
式中Ud、id、Ld分别为d轴电压、电流和电感;Uq、iq、Lq分别为q轴电压、电流和电感;Rs为绕组电阻;ωe为转子电角速度;ψd和ψq分别为d轴和q轴磁链;ψf为永磁体磁链;p为电机极对数;Te为电磁转矩;TL为负载转矩;J为转子转动惯量;ωm为转子机械角速度。
2 矢量控制原理
矢量控制是20世纪70年代为解决三相异步电机难以调速问题而提出[7-8]。其原理是在保障恒功率、磁动势不变条件下,将三相静止坐标系下定子电流矢量通过Clark变换和Park变换转换成转子磁场定向的两个直流分量id(励磁电流分量)和iq(转矩电流分量),这种方法实现了模拟控制直流电机的方式分别控制磁链和电磁转矩。
对表贴式PMSM,根据矢量控制原理构建的PMSM矢量控制框图见图1,由速度环和电流环组成。速度环输出量iqref作为转矩电流环输入,令励磁电流环输入id=0,由电流环输出得到两相静止坐标系下定子相电压分量,对其进行Park逆变换得到同步旋转坐标系下定子相电压矢量Uα和Uβ。利用SVPWM技术产生脉宽调制波对逆变器进行调制,实现对PMSM驱动。
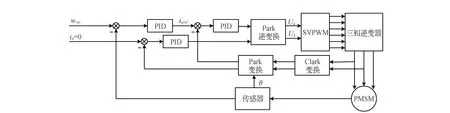
图1 PMSM矢量控制框图Fig.1 PMSM vector control block diagram
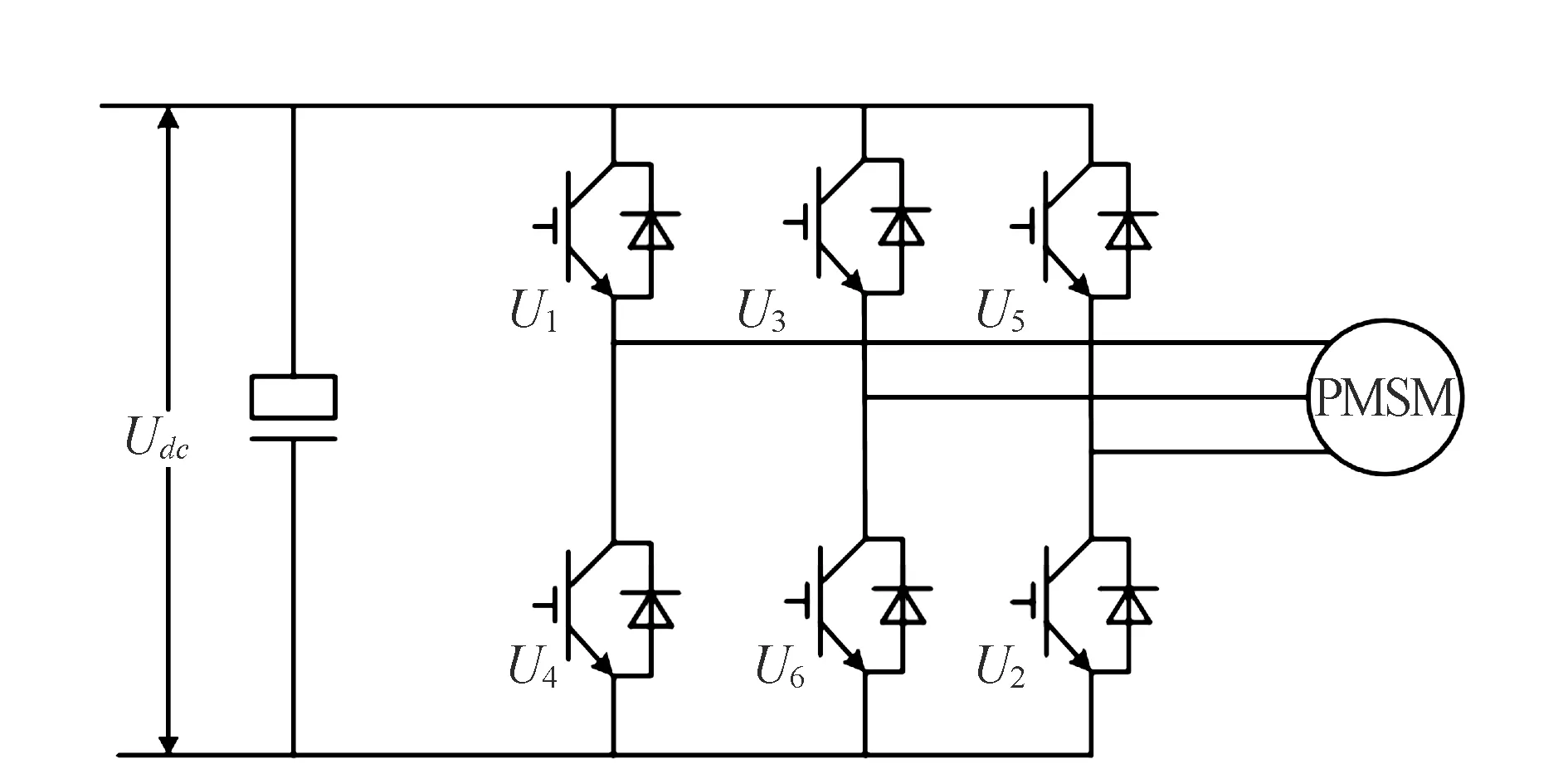
图2 逆变电路Fig.2 Inverter circuit diagram
3 SVPWM原理
SVPWM工作原理是在一个开关周期内将逆变器的开关元件进行组合产生基本电压矢量,使其平均值与目标电压矢量相等。在某个区域目标电压矢量可由其相邻的零矢量与非零矢量在时间上不同组合得到,通过控制各个电压矢量作用时间,可使电压矢量按照圆形轨迹旋转。
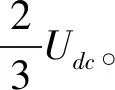
电压空间矢量见图3,目标电压矢量Uref可由所在区域内相邻两个矢量合成得到。假设Uref位于扇区Ⅰ,可将Uref表示为:
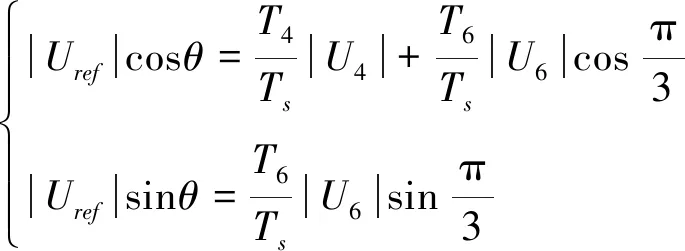
(4)
式中Ts为载波周期;T4、T6分别为电压矢量U4(100)、U6(110)作用时间。
根据开关管开关顺序,在扇区Ⅰ内一个载波周期产生PWM波形见图4,电压矢量的切换顺序为U0、U4、U6、U7、U6、U4、U0。此方法称为七段式SVPWM调制,优点是可减少逆变器的开关损耗。实现上述调制首先要找到目标电压矢量Uref所在扇区,并计算其相邻矢量作用时间。
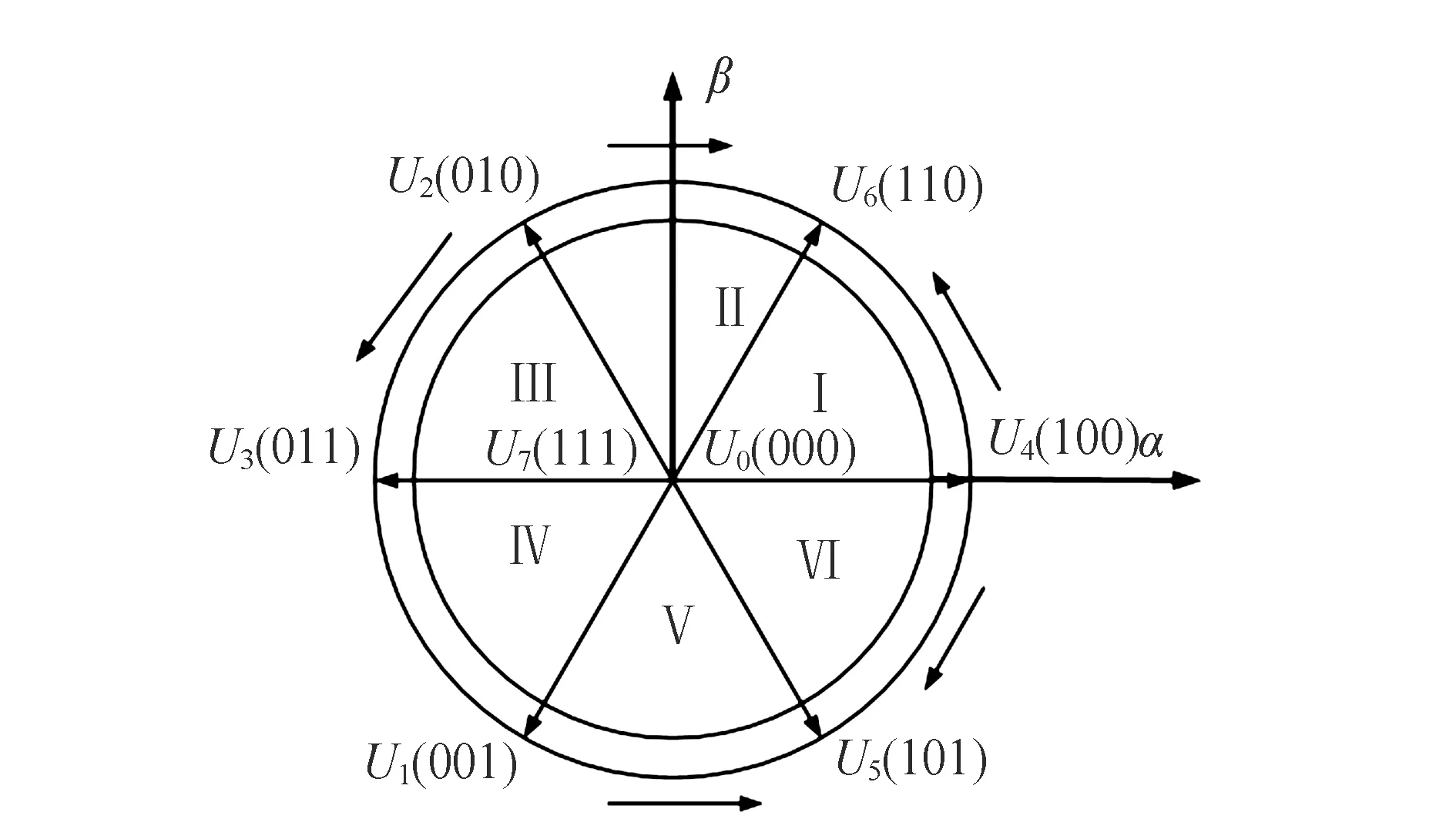
图3 电压空间矢量图Fig.3 Voltage space vector diagram
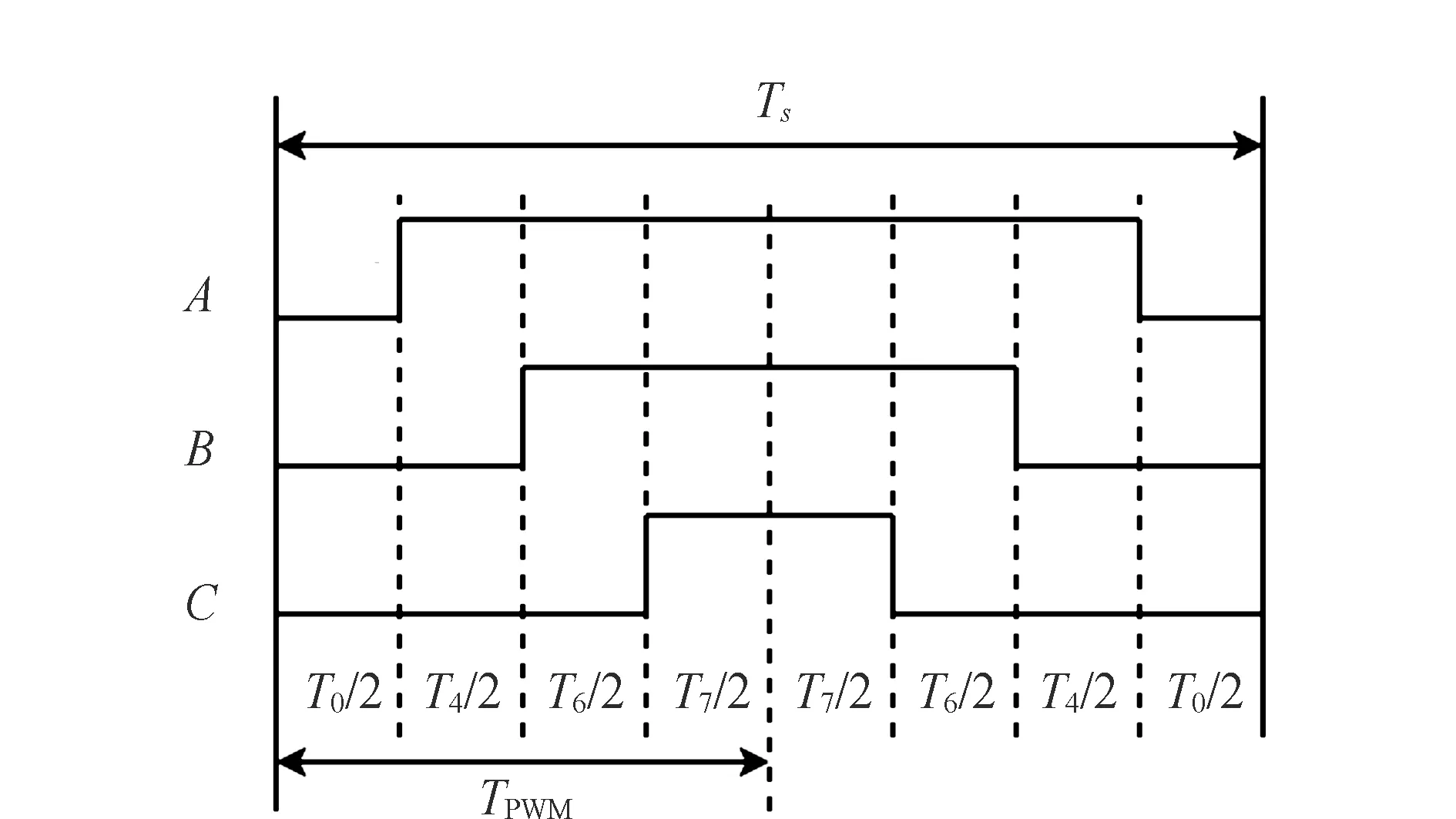
图4 扇区Ⅰ内PWM波形Fig.4 PWM waveform in sector Ⅰ
3.1 扇区判断
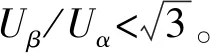
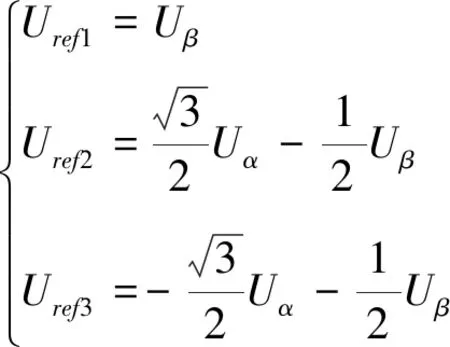
(5)
定义变量A、B、C:若|Uref1|>0,则A=1,否则A=0;若|Uref2|>0,则B=1,否则B=0;若|Uref3|>0,则C=1,否则C=0。令N=4C+2B+A,则A、B、C共有8种组合。由于不可能同时为0,所以实际组合只有6种,可以确定目标电压矢量所在扇区,N与扇区对应关系见表1。
3.2 矢量作用时间计算
将在扇区Ⅰ的Uref在α、β坐标系下进行分解,利用该坐标系下电压矢量Uα、Uβ以及载波周期Ts,计算出扇区Ⅰ内的矢量作用时间T4、T6、T0和T7。

表1 N值与扇区对应关系
(6)
根据式(5)和式(6)可得:
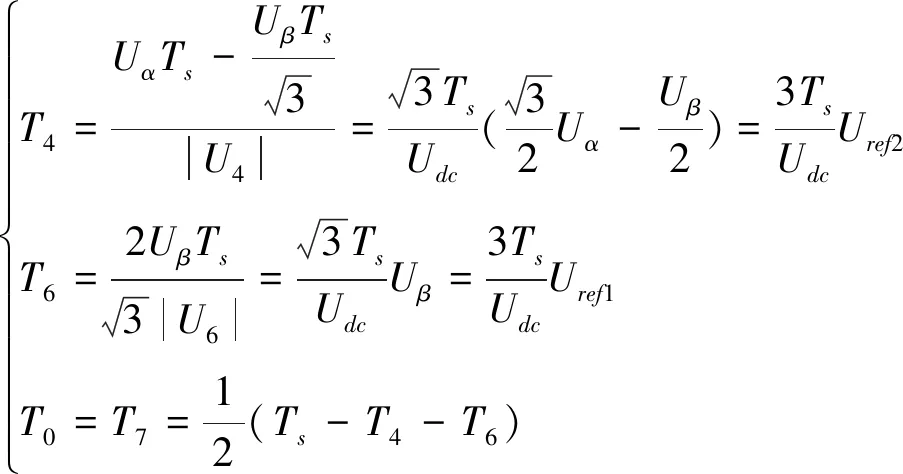
(7)
同理可求得Uref在其它扇区时的作用时间。
设变量X、Y、Z,其计算公式为:
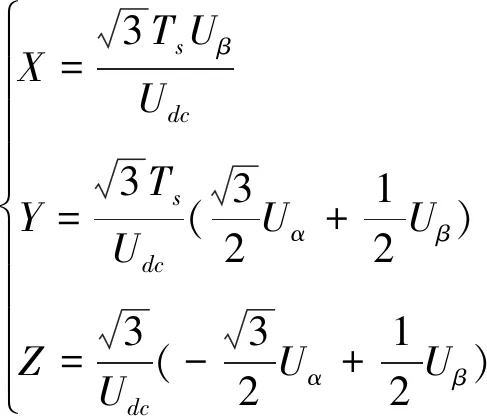
(8)
利用式(8)可以表示出每个扇区下电压矢量作用时间,也能计算出在不同扇区下PWM占空比。在MATLAB/Simulink下对SVPWM各个部分封装,SVPWM模块框图见图5。
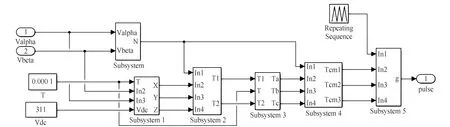
图5 SVPWM模块框图Fig.5 SVPWM module block diagram
将SVPWM应用到永磁同步电机控制上,可提高直流母线电压利用率,减小绕组电流谐波分量,降低直接转矩脉动,旋转磁场更接近圆形。在直流电机控制中存在的快速和超调矛盾,在SVPWM永磁同步电机控制中依然存在,考虑对速度给定信号进行跟踪微分处理,然后安排过渡过程解决这一矛盾。
4 安排过渡过程
最速跟踪微分器数学表达式为[9]:
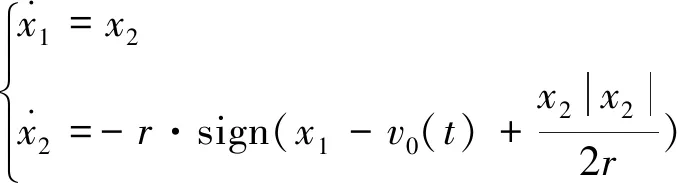
(9)
式中x1(t)为跟踪速度环给定信号v0(t);x2(t)为跟踪v0(t)微分信号;r为速度因子。
r值越大,跟踪速度越快,但是在系统进入稳态时会产生高频震荡,这是因为开关线两边状态反馈量在±r之间的不断切换所产生的。为了消除这种影响,将开关函数sign(·)改成线性饱和函数sat(·,d),其中d为线性区间。饱和线性函数关系式为:
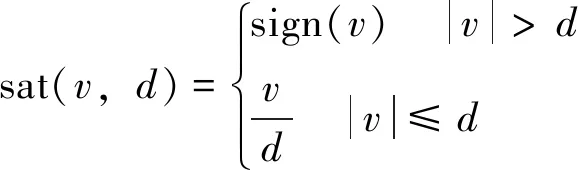
(10)
利用MATLAB的S函数编写跟踪微分器和饱和函数,永磁同步电机调速系统仿真图见图6。
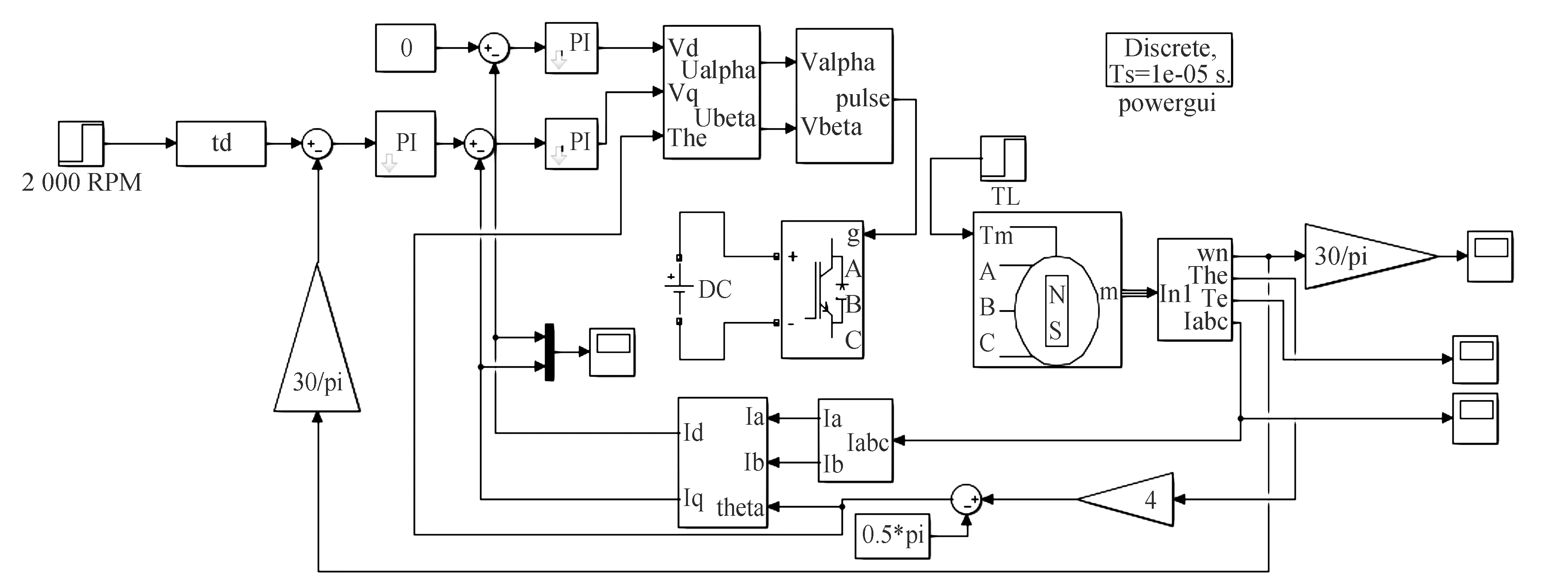
图6 永磁同步电机调速系统仿真图Fig.6 Simulation diagram of PMSM speed control system
5 数值仿真
采用表贴式PMSM,具体参数见表2。
仿真时间设置为1 s。在0 s令电机空载启动,给定速度为2 000 r/min,在0.5 s加入1 N·m阶跃负载。跟踪微分器参数取r=1 000 000、d=5。
电机速度运行曲线见图7,直接启动时有10%超调,安排过渡过程后接近无超调,且两种控制方法调节时间相当,可见安排过渡过程可以改善系统控制性能。id、iq电流曲线见图8,定子电流曲线见图9。电机启动时电流波动较大,在0.06 s后很快达到稳态。在0.5 s加入阶跃负载,电流快速调节并在很短时间内达到稳态。电磁转矩曲线见图10,启动转矩较大,加速性能强。在加入阶跃负载后,电磁转矩快速达到1 N·m。
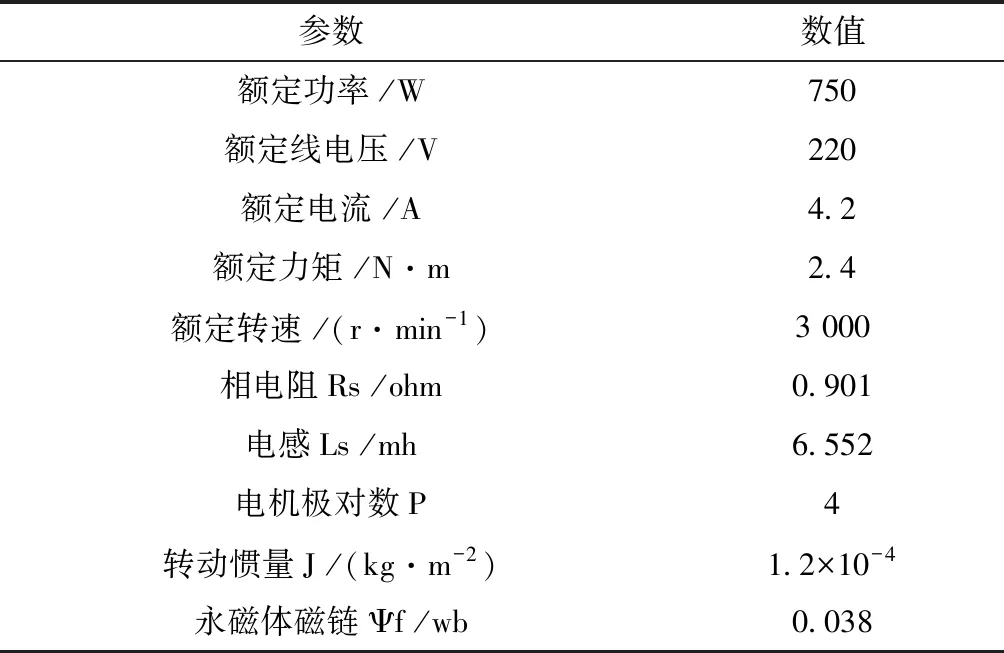
表2 电机参数
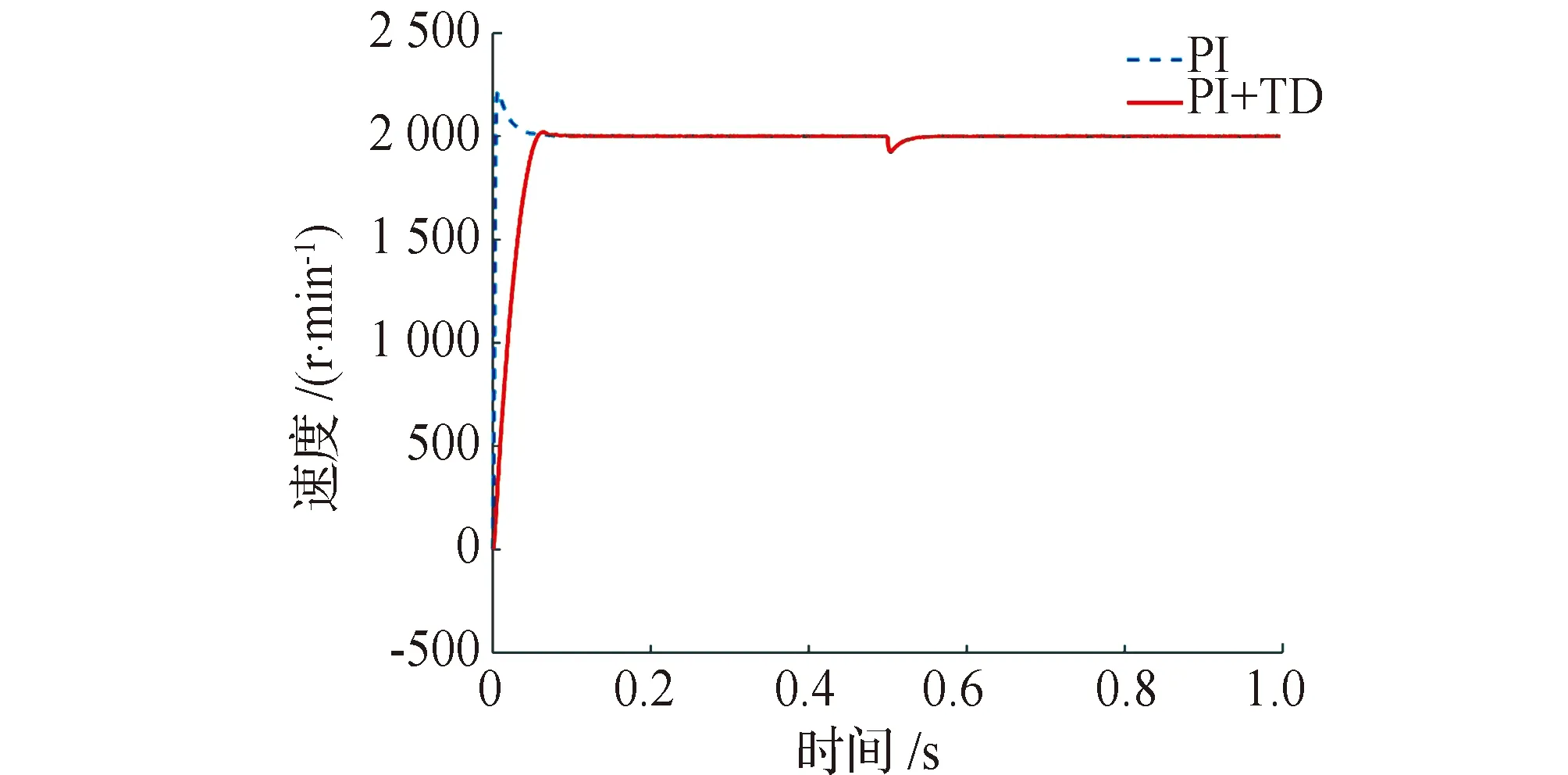
图7 电机速度运行曲线Fig.7 Motor speed running curve
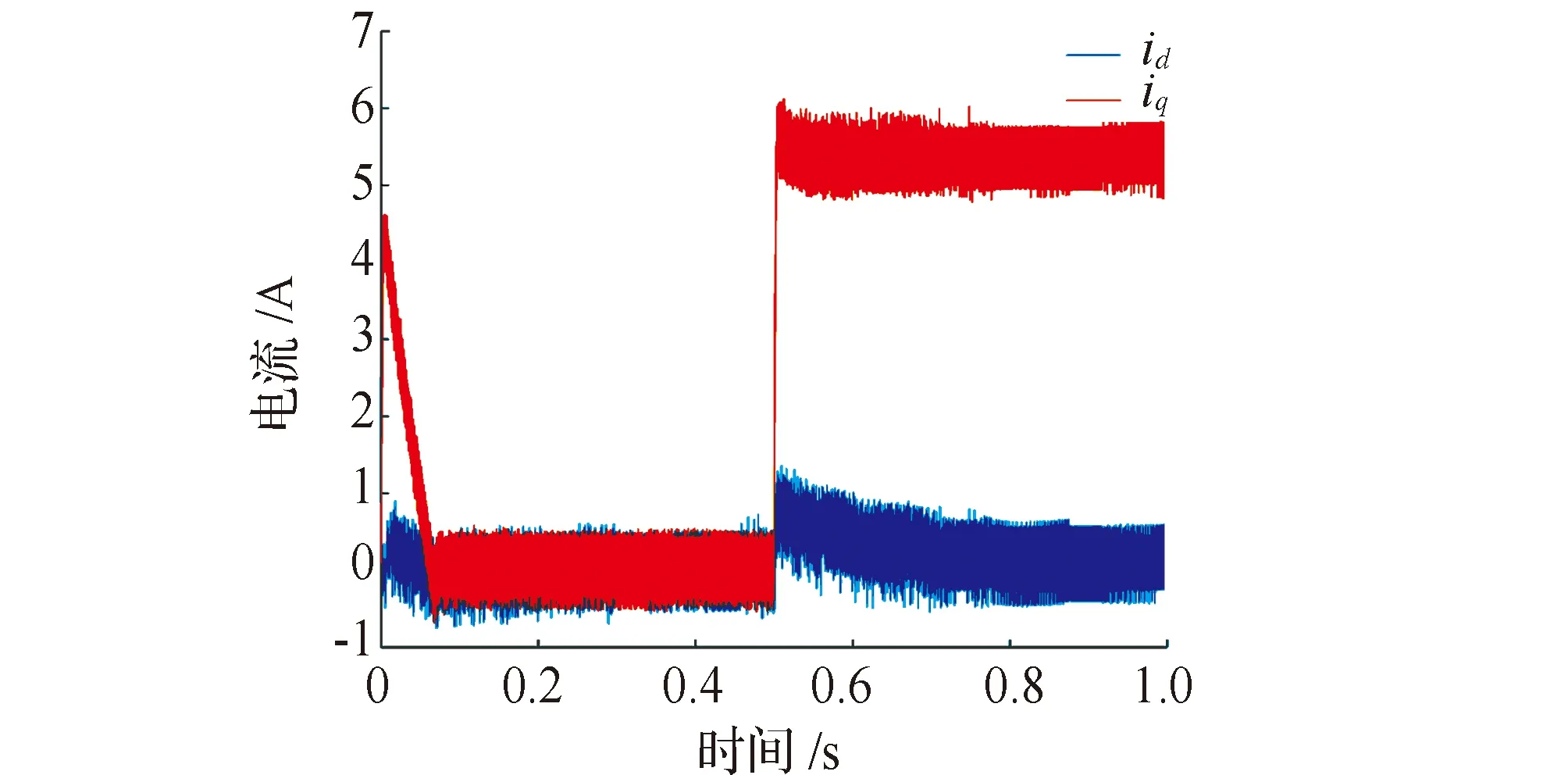
图8 id、iq电流曲线Fig.8 id,iq current curve
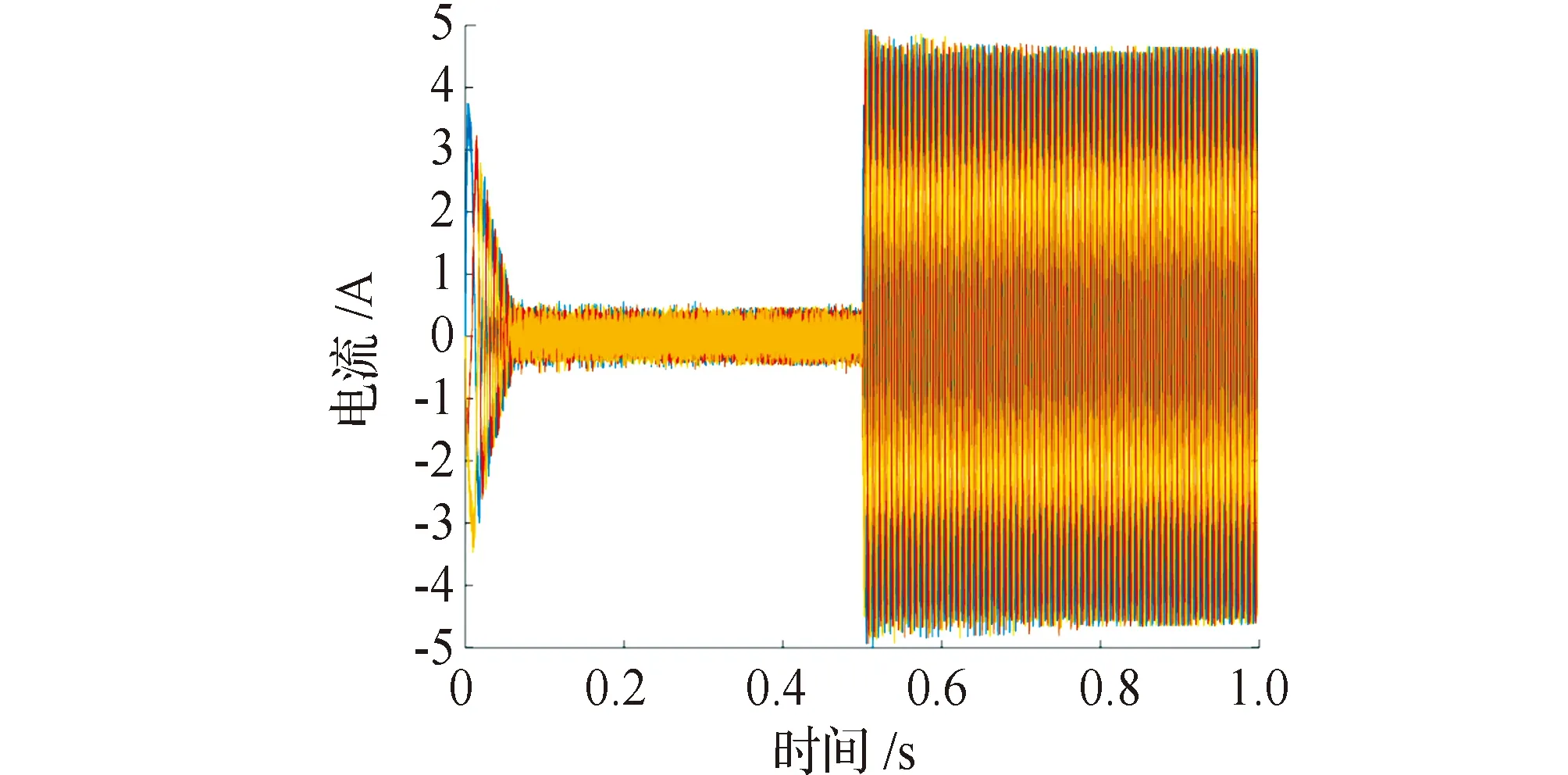
图9 三相定子电流曲线Fig.9 Three-phase stator current curve
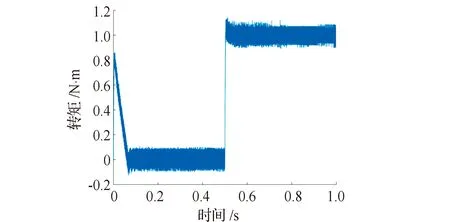
图10 电磁转矩曲线Fig.10 Electromagnetic torque curve
6 结 论
本文研究了基于SVPWM永磁同步电机调速系统控制问题。首先建立交流永磁同步电机数学模型,分析矢量控制原理,推导SVPWM工作过程并进行模块封装,引入安排过渡过程解决PID控制器超调大的问题。所得控制器应用于永磁同步电机调速系统仿真过程,达到预期的控制效果。
