特高压变电站构架节点半刚性影响研究

翟 彬，王慧慧，商文念

(山东电力工程咨询院有限公司，济南 250013)

0 引 言

随着我国电力需求持续增加，特高压变电站陆续建成。1 000 kV构架是特高压变电站内重要的建构筑物之一，承担着变压出线的支撑作用，具有跨度大、高度高及结构形式复杂等特点。由于缺乏相应规范的指导，目前1 000 kV构架的设计仍将节点假定为刚接或铰接处理，与实际工程结构中节点的刚度情况不符，如若对节点刚度进行较为系统地分析并在设计时考虑节点半刚性的影响，这样的设计无疑会更加经济和准确[1]。国内外学者对节点半刚性的研究主要在半刚性节点的连接计算方法和以大量的试验为依据来验证半刚性连接节点的静动力性能[2]。节点半刚性的研究多用于钢框架结构[3-6]和大跨钢结构[7-10]。对于输电塔、构架这类具有复杂节点形式的结构，钱程等[11]研究了节点半刚性对输电塔峰值响应的影响，发现当节点转动刚度接近刚接时，主材的弯曲应力占总应力的10%～15%。赵楠[12]研究了角钢作为主要承重构件的750 kV输电塔结构，对比铰接模型，发现节点半刚接模型使主材应力减少39.05%，静力承载力可提升35%，且整体性更好。安利强等[13]研究了节点半刚性对钢管塔导地线挂点位移的影响，发现随着节点刚度变大，大风工况下位移变化百分比最大为25.58%，断线工况最大为65.99%。以上针对输电塔节点半刚性的研究已经表明，实际工程设计分析中将节点假定为刚接或铰接并不准确，考虑节点半刚性特性对于准确获得结构的响应具有重要意义。截至目前针对构架的研究成果尚少，规范中也未提及考虑构架节点半刚性的应对措施。传统设计方法常将桁架结构的节点按照铰接或者刚接设计，与实际结构的静力性能或动力性能存在较大误差。杨靖波等[14]进行了1 000 kV交流特高压双回路SZT2钢管塔足尺试验，研究表明结构响应实测值明显小于计算值，这主要是由于计算模型采用铰接节点，试验模型采用半刚性节点。除此之外，学者们还研究了变电构架节点力学性能[15-16]、节点及构架的优化选型[17-18]和构架的动力分析[19-20]。

本文以某特高压变电站出线构架为研究对象，对其不同连接形式的节点进行非线性有限元分析，讨论了各类节点的破坏机理并获得了其弯矩-转角曲线，建立基于半刚性的构架整体有限元模型，对比讨论其与刚性构架的静力性能，并提出工程设计建议。

1 有限元模型的验证

半刚性节点的有限元分析能够反映其基本的受力性能，但仍然属于理想的简化模型，准确性需要相关的试验加以佐证。本文将依托文献[12]中的输电塔角钢K型节点试验，验证半刚性节点有限元模型的正确性及建模方法的有效性。

1.1 输电塔角钢K型节点试验

文献[12]为了获得K型节点的弯矩-转角曲线，开展了静力试验。其中钢材强度为Q420，角钢构件尺寸为L160 mm×160 mm×10 mm，节点板厚度取10 mm，螺栓为8.8级高强螺栓，间距为100 mm，试验见图1。

两个千斤顶同时分级加载，在弹性阶段持荷3 min，弹塑性阶段持荷10 min。采用百分表测量主角钢剪切域的转角，位移计测量整个节点域的转角。

1.2 数值仿真与试验对比

有限元模型采用实体单元SOLID95模拟角钢、节点板和螺栓，材料属性与试验实测值相同，模型各个接触属性为沿切面方向设置0.35的摩擦系数，法向为硬接触，数值仿真的加载工况和试验工况相同，有限元模型见图2，数值与试验对比见图3。

图3(a)为文献[12]试验和有限元分析的弯矩-转角曲线，图3(b)为本文数值仿真的弯矩-转角曲线。通过对比发现本文与文献[12]获得的弯矩-转角曲线结果吻合度较高，在加载后半程试验值较有限元值略大，主要是在有限元分析中模型具有理想约束，外界干扰较少。总体上有限元值和试验值基本吻合，验证了本文建模方法的可靠性。

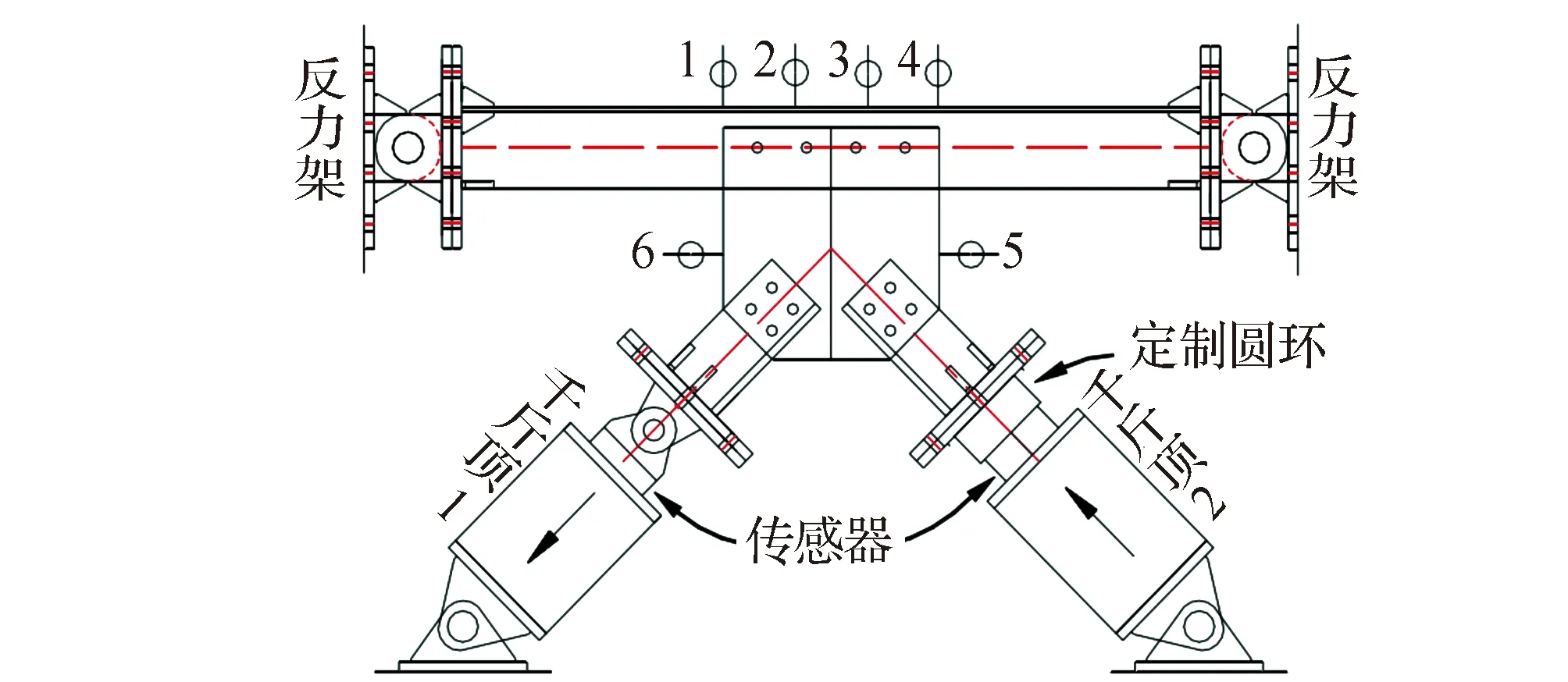
图1 输电塔角钢K型节点试验Fig.1 K-joint test of transmission tower angle steel

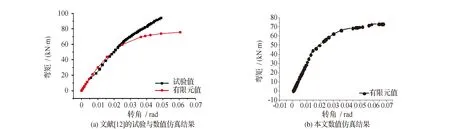
图3 数值仿真和试验弯矩-转角曲线对比Fig.3 Comparison of moment-rotation curves obtained by numerical and experimental investigation

2 构架节点的弯矩-转角关系模型

为了开展基于节点半刚性的1 000 kV构架静力分析，将选取构架的典型节点，分别对不同类型典型节点进行非线性分析，研究其弯矩-转角关系及半刚性属性。

2.1 典型节点的选择

通过归纳分析1 000 kV构架的节点形式，按照简单实用原则，将构架数以百计的节点根据插板连接形式的不同而划分为3类节点，分别为C型插板连接节点、T型插板连接节点和十字型插板连接节点，见图4。每一类型连接节点再根据主支管尺寸、螺栓个数和排列方式进一步划分，得到构架的关键节点种类，见表1。

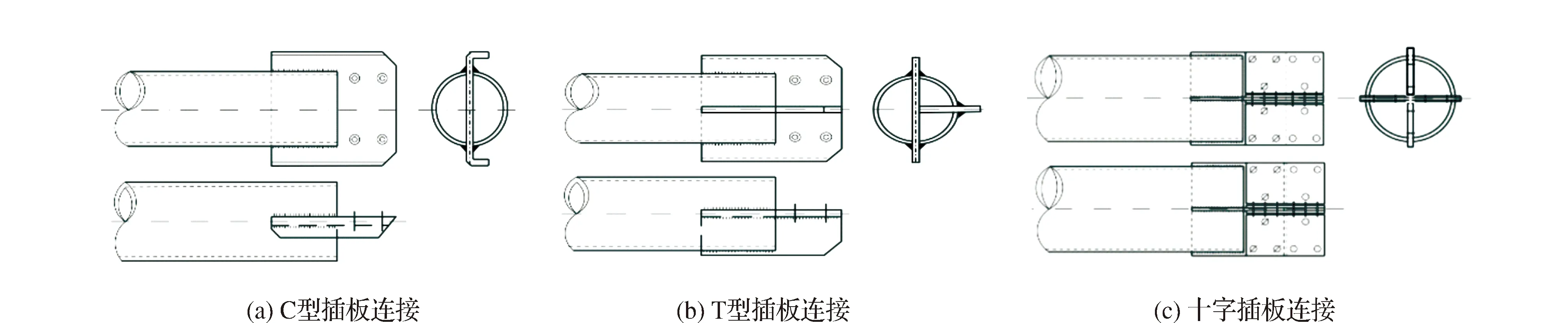
图4 构架节点分类Fig.4 Classification of OLF1 000 joints

表1 构架关键节点

2.2 C型插板连接节点破坏机理

C型插板连接是1 000 kV构架中应用最多的连接形式，采用前述建模方法分别建立节点K-1、K-2及K-3，见图5。

图5 C型插板连接节点Fig.5 C-type plate joints

有限元分析采用分级加载的形式，直至节点域出现较大塑性变形为止。K-1、K-2和K-3的破坏模式基本相同，均是螺栓发生剪切破坏而致使节点失效，见图6。其中K-1节点离支管较近的螺栓率先出现屈服，K-2节点的两个螺栓同时发生相反方向的剪切破坏，K-3节点的螺栓群出现沿顺时针方向的剪切破坏。支管插板和主管节点板均未到达屈服，未发生螺孔处的挤压变形。因此，C型插板连接节点以螺栓的剪切破坏为控制条件。

图6 C型插板连接节点螺栓破坏Fig.6 Bolt failure in C-type plate joints

2.3 T型插板连接节点

开展T型插板连接节点静力分析时有两点假设：①K字型节点模型中两分肢管之间互不影响，在研究节点刚度时只需考虑单根管的作用；②只考虑弯矩作用面内刚度，忽略面外刚度的影响。T型插板连接节点的有限元模型见图7(a)。根据非线性分析结果发现：在加载初期，主管和支管之间力的传递首先靠螺栓群最外侧靠近分肢管的两个螺栓抵抗剪切力的作用，随着荷载值增大，螺栓和节点板之间产生挤压作用，使靠近肢管侧加劲板和主管连接处产生应力集中现象，最后随着弯矩值继续增大，螺栓群变形较小，T型插板产生较大的弯曲变形，见图8(a)。T型插板连接节点以T型插板的弯曲变形为控制条件。

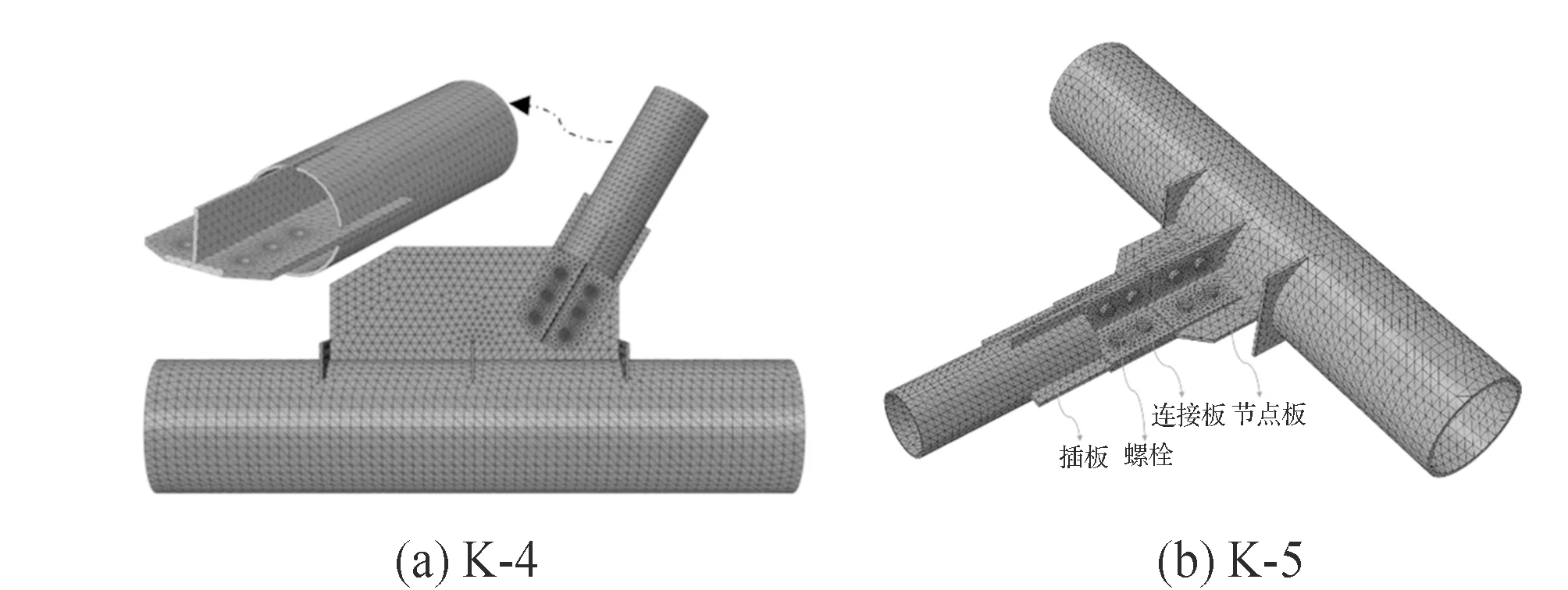
图7 T型插板和十字型插板连接节点Fig.7 T-type plate joints and cross-gusset plate joints

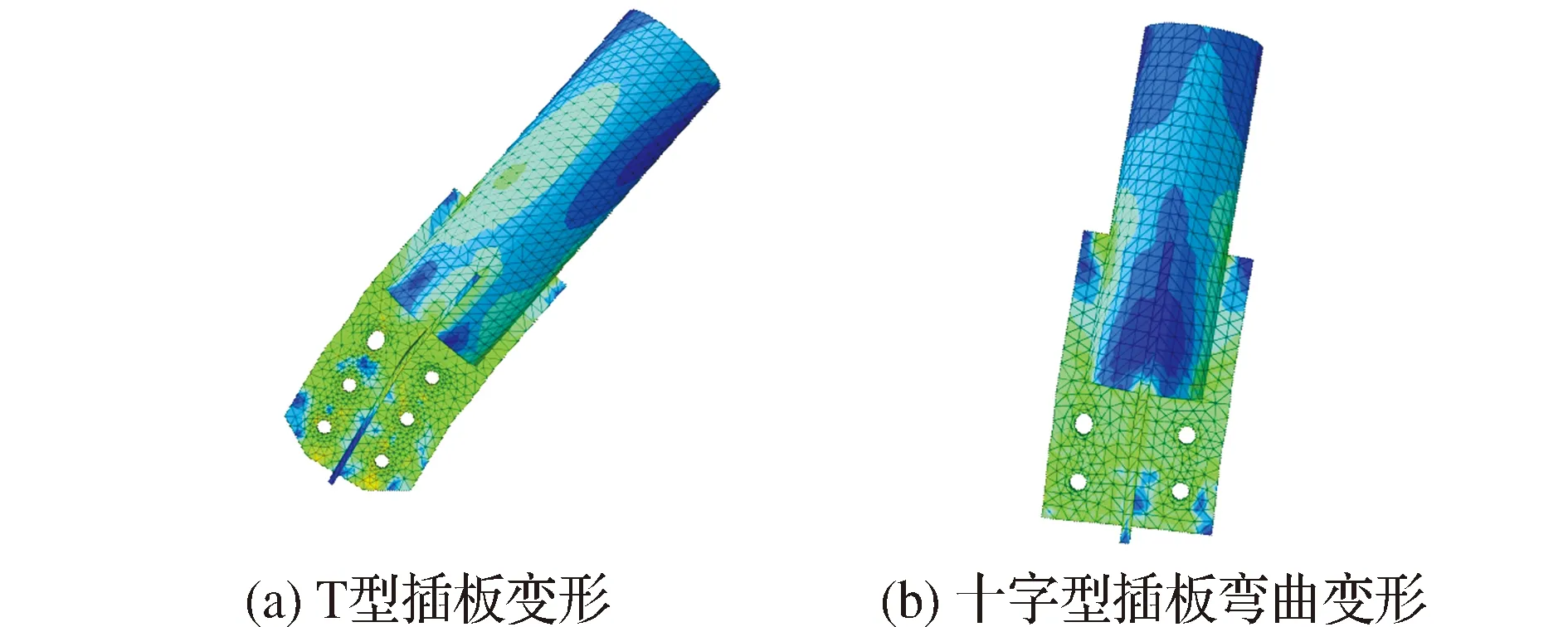
图8 T型插板和十字型插板连接节点有限元分析结果Fig.8 FE analysis results of T-type plate joints and cross-gusset plate joints

2.4 十字型插板连接节点

十字型插板连接节点由十字型节点板、十字型插板、连接板和螺栓群组成，见图7(b)。在十字型节点板连接节点加载过程中，随着荷载值的增大，首先与加劲板平行方向的节点板部位发生螺栓群受拉和剪切力的作用，在加劲板和主管连接处发生应力集中现象。持续增大荷载值，靠近主管的螺栓群受到更大的剪切力作用，但仍有较大的强度富裕，最后整个模型因为节点板部位发生较大的弯曲变形而破坏，见图8(b)，16个螺栓皆有较大的强度富裕，没有发生预想中主管局部失稳现象。

2.5 不同节点弯矩-转角曲线比较

为了获得各类节点的弯矩-转角曲线，定义节点转角见图9，其中包括主钢管的剪切转角和节点板相对主钢管的转角，公式为：

(1)

式中θi为节点板第i个端点的转角；θm为主钢管的剪切转角；n为节点板的端点数目。

对各类型节点开展有限元非线性分析，获得其弯矩-转角曲线见图10。由图10可见，曲线K-1和K-2节点性能与螺栓的排列形式基本无关，与各螺栓离形心的距离相关；节点性能与插板的螺栓数目相关，螺栓数量越多，节点初始刚度越大；相同插板螺栓数目，十字节点的性能明显优于C型节点，其中初始刚度提高了2倍，极限承载力提高了2.5倍，而且即便T型插板螺栓数目多于十字插板，但T型节点极限承载力仍然低于十字型节点25%，这是因为十字型节点在弯矩作用平面内的截面惯性矩更大。

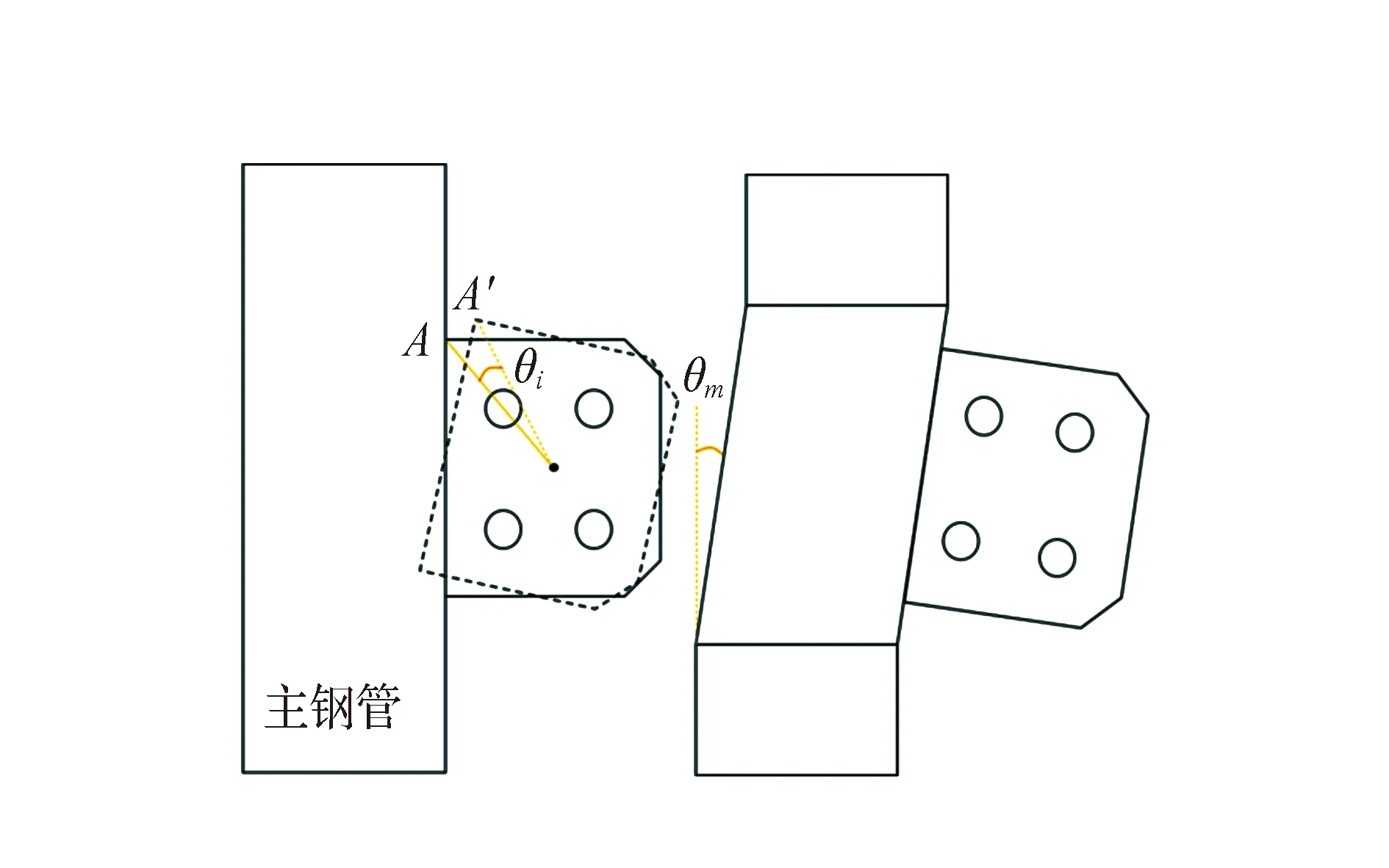
图9 钢管节点转角组成Fig.9 Rotation composition of steel tube joints

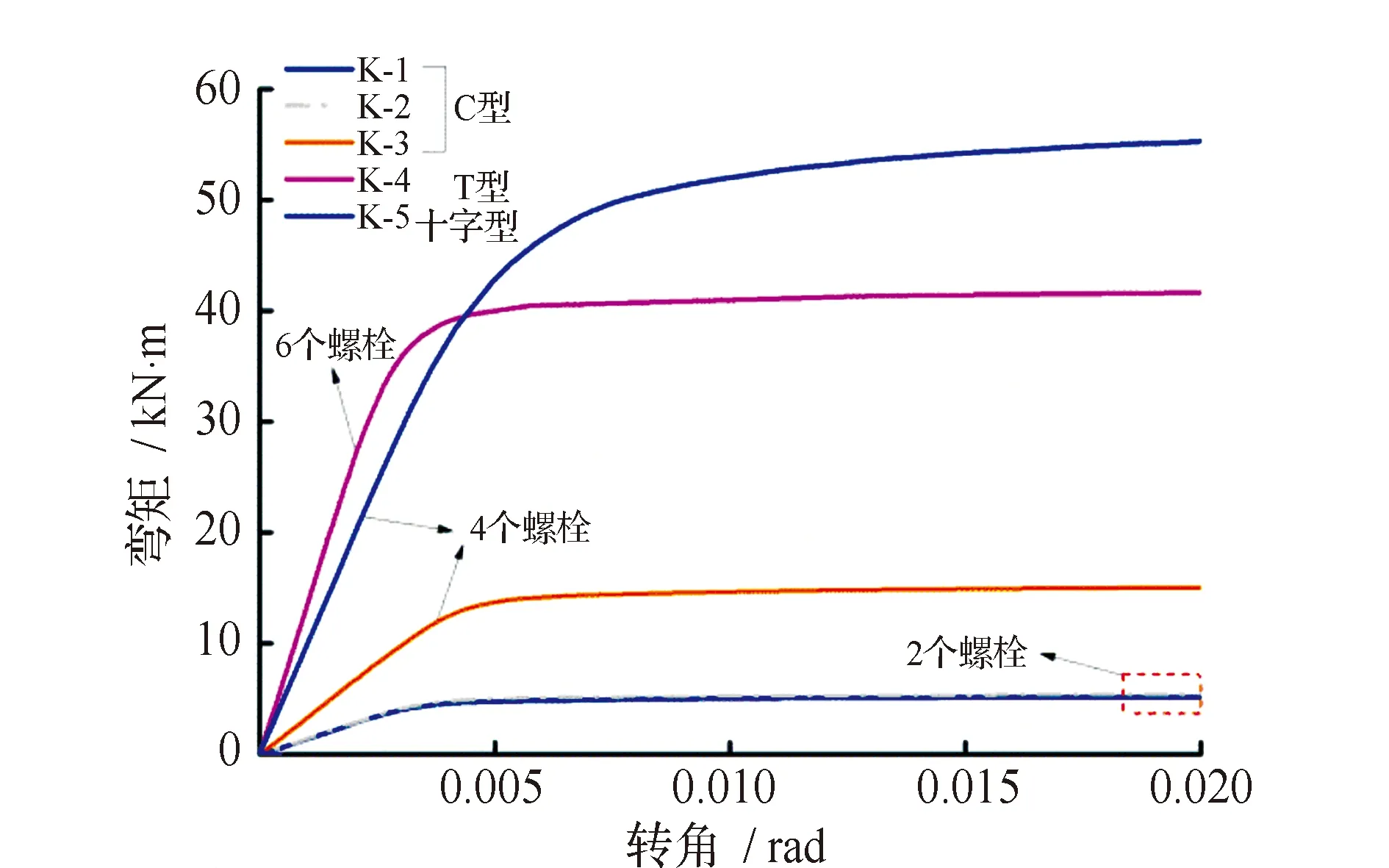
图10 节点弯矩-转角曲线Fig.10 Moment-rotation curves of joints

3 基于半刚性节点的构架静力性能分析

3.1 构架数值模型

依据某1 000 kV构架图纸，本文采用ABAQUS有限元软件分别建立构架的刚性节点模型和半刚性节点模型。构架的尺寸见图11，其中柱脚尺寸为3 m×9 m，梁截面尺寸为3 m×3 m；选用Q345B级钢材，弹性模量和屈服强度分别为2.06×105MPa和310 MPa，泊松比取0.3，密度为7 850 kg/m3。刚性节点模型各杆件之间全部采用刚性连接。

在半刚性节点构架建模过程中，杆件两端分别设置长度足够小的节点域，杆件与节点域采用连接单元结合。零长度的连接单元需设立绕Y轴和Z轴的抗弯刚度及绕X轴的扭转刚度。其中抗弯刚度均采用前述的弯矩-转角曲线进行定义，扭转刚度取为无限大。格构梁和格构柱的弦杆之间采用刚性连接，而腹杆与弦杆之间采用基于连接单元的半刚性连接。本文详细分析了构架各节点的类型，分别添加第2节中K1～K5的半刚性属性。

3.2 节点刚度对结构静力性能的影响

在进行1 000 kV构架的设计时考虑的工况复杂，包括大风、覆冰、安装和紧线等。本节仅考虑结构自重、导线张力荷载及悬挂金具荷载，见图11。分别对刚性节点构架和半刚性节点构架开展静力分析，分析比较两种模型的结构响应，包括最大位移、最大应力和极限荷载。

两种模型在设计荷载和极限荷载下的结构响应见图12，分析发现对结构施加设计荷载时，结构弦杆受力明显大于腹杆，说明结构在静力作用下以受弯为主，而且刚性构架的结构响应略低于半刚性构架，最大减小10.9%。经过计算，刚性构架的极限荷载大约是半刚性构架极限荷载的2.3倍，构架以刚性节点设计时将高估实际结构的承载力，而且也将对杆件截面的选取存在影响。

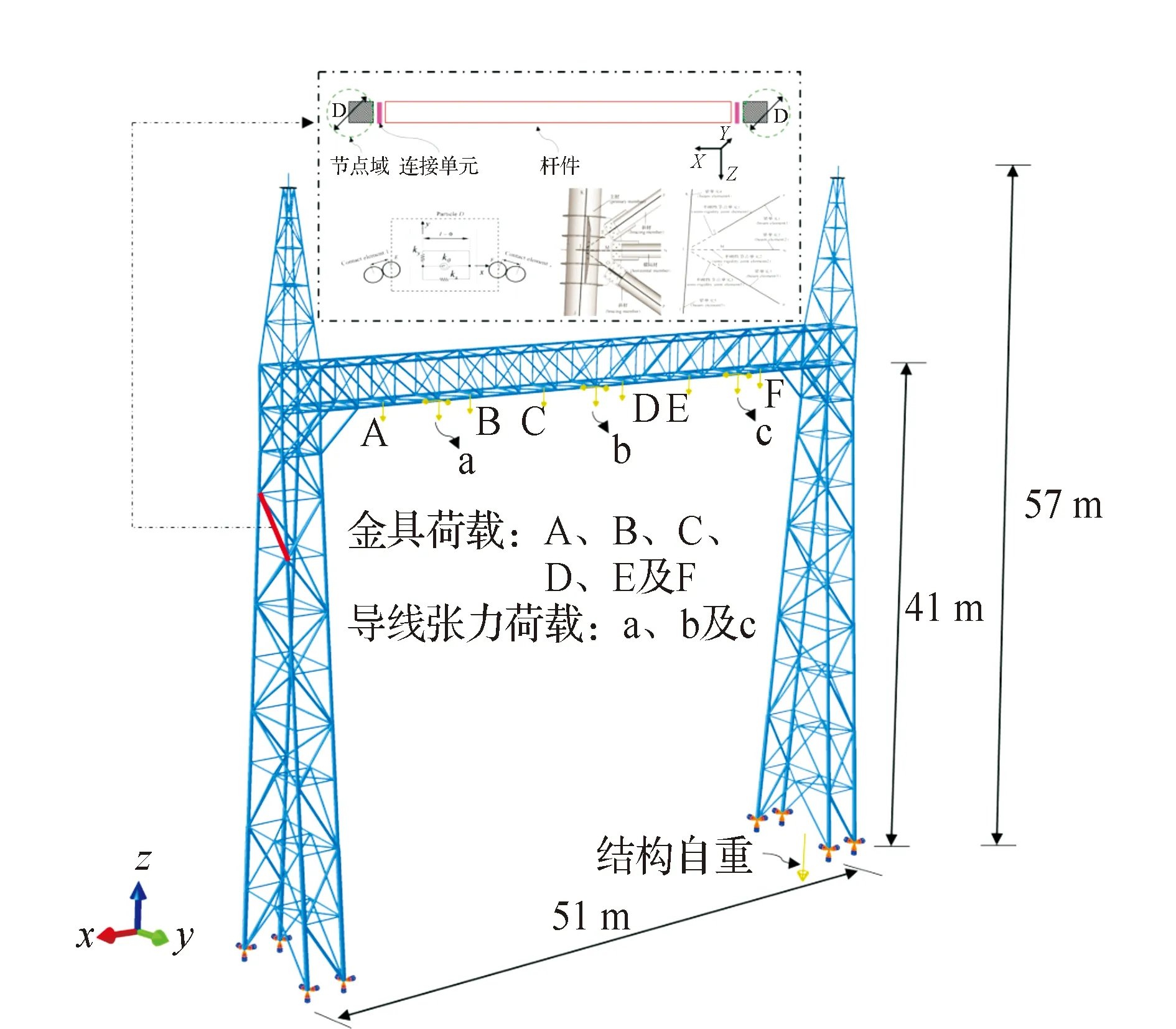
图11 1 000 kV构架模型Fig.11 FE model of OLF1 000

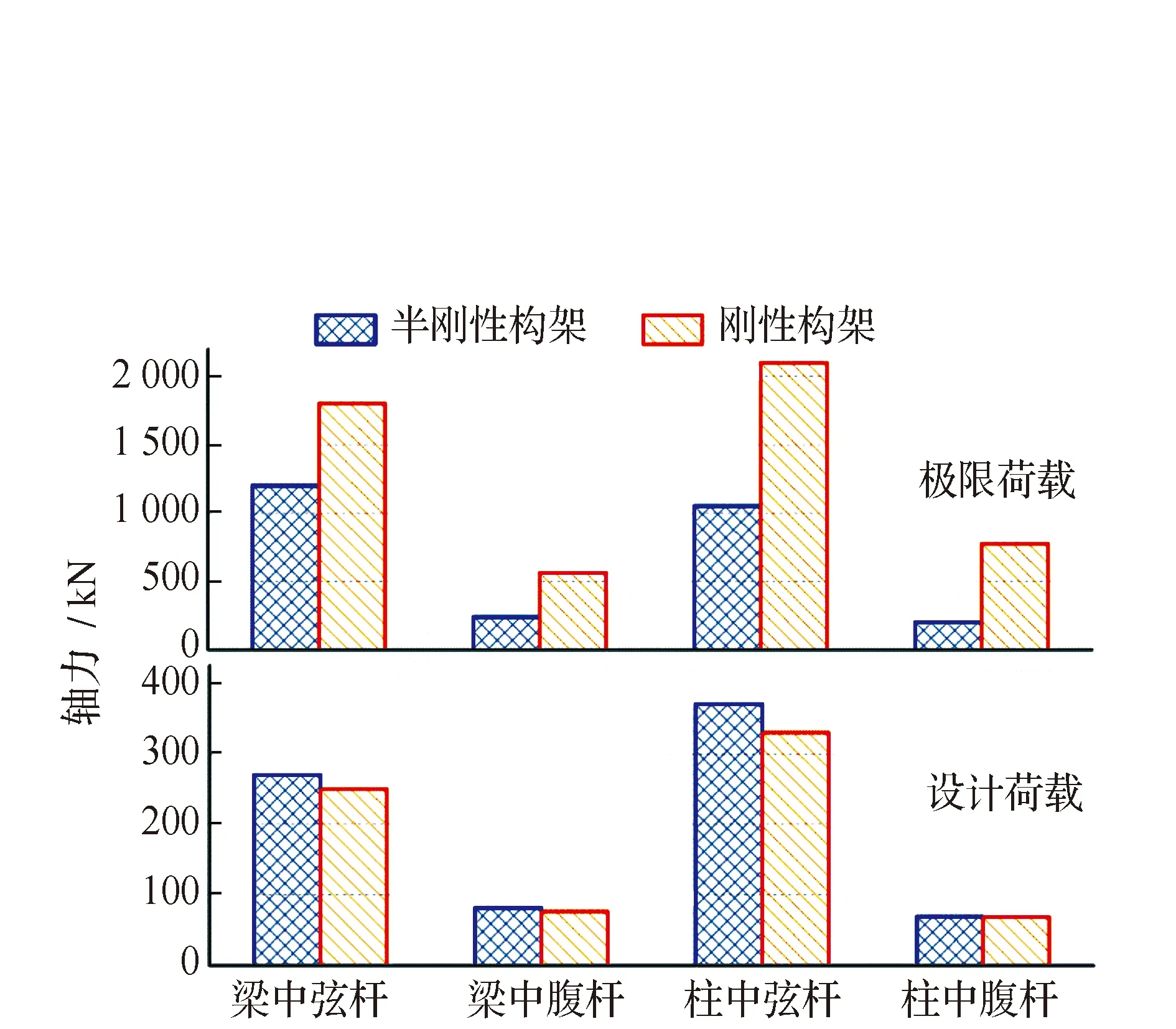
图12 2种模型在设计荷载和极限荷载下的结构响应Fig.12 Structural response of two models under design and ultimate loads

为了更直观描述节点刚度变化，引入刚度变化因子ε，它是实际分析刚度和初始分析刚度的比值。

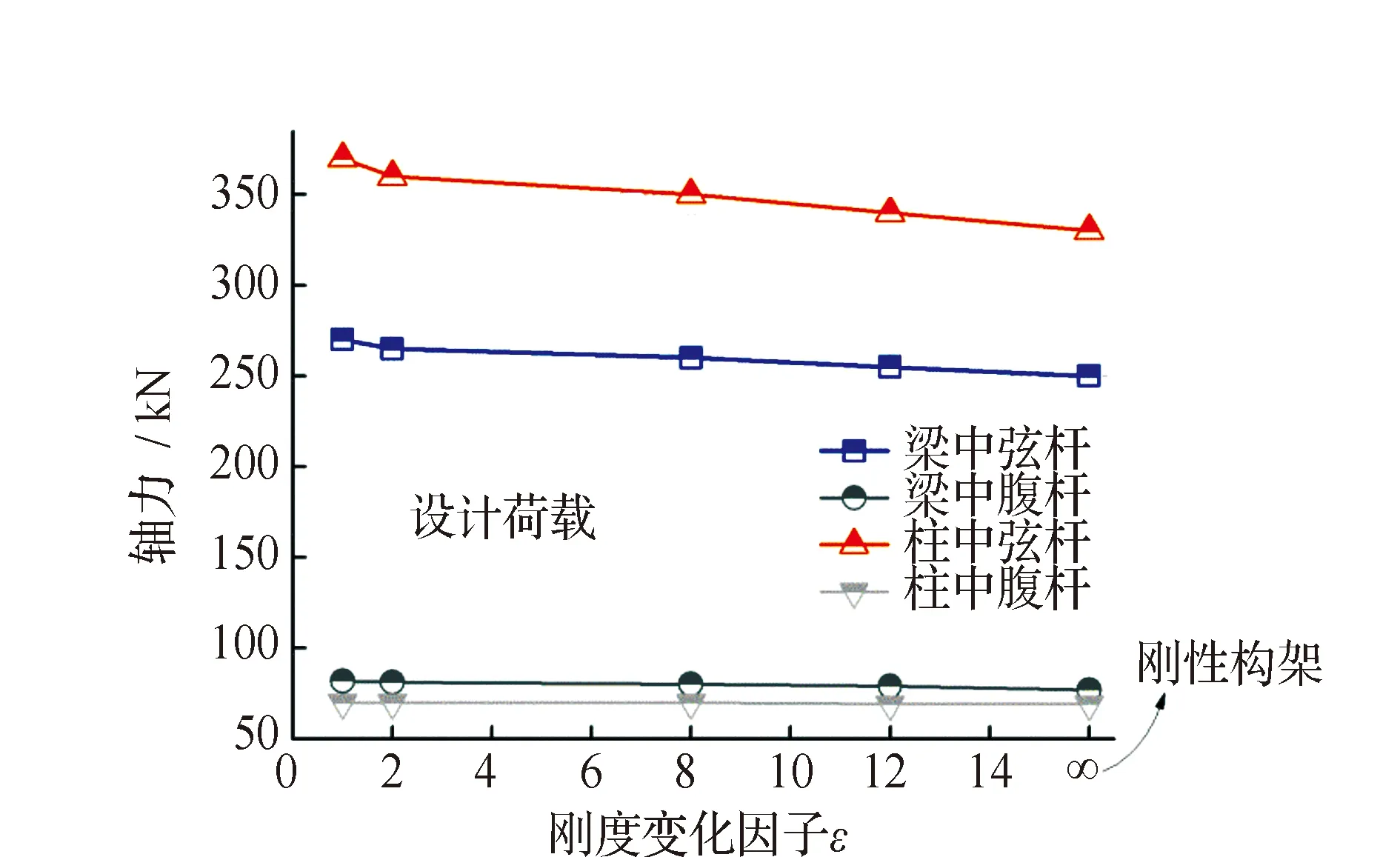
图13 节点刚度对构架响应的影响Fig.13 Effect of joint stiffness on OLF1 000 responses

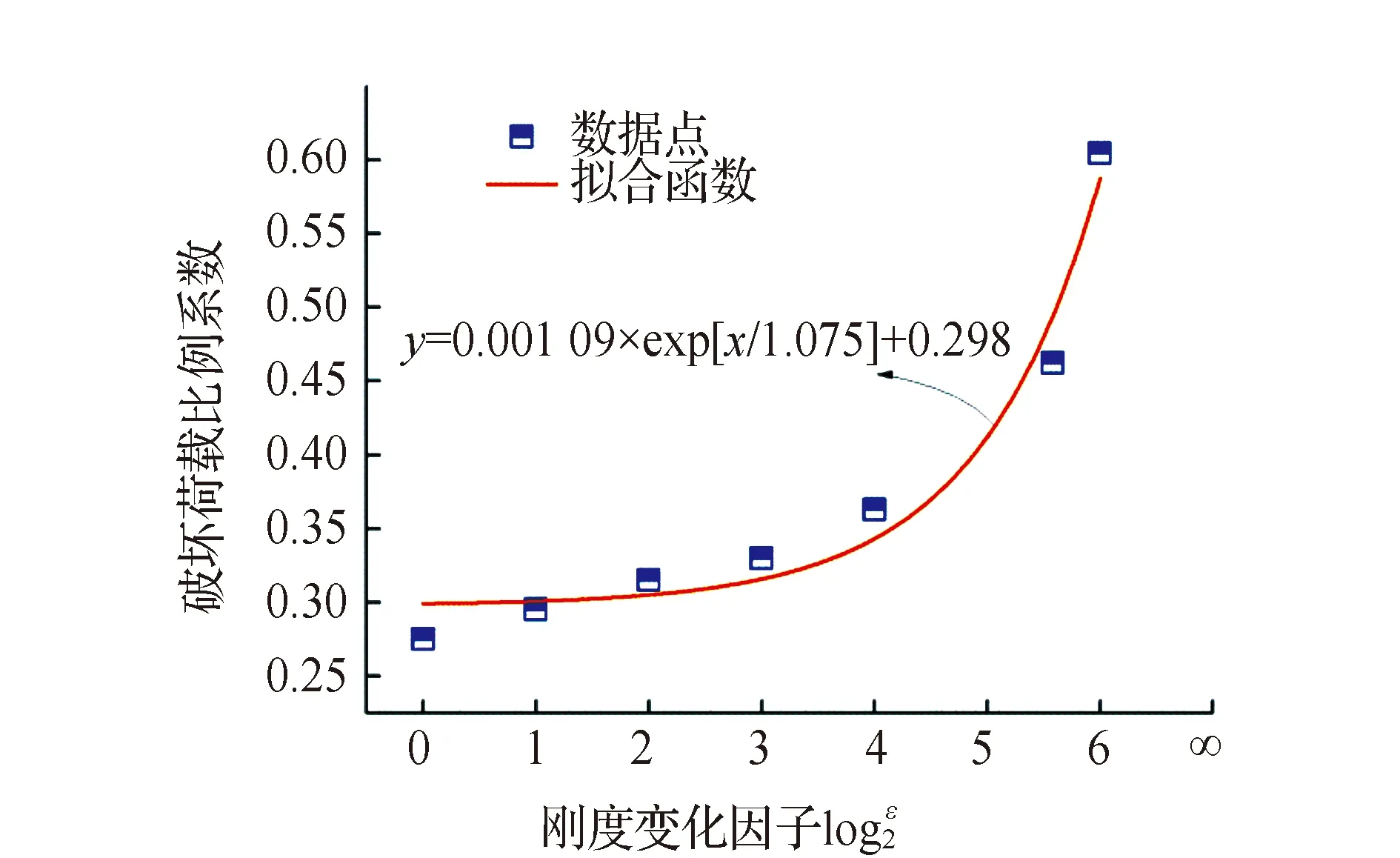
图14 节点刚度对承载力的影响Fig.14 Effect of joint stiffness on bearing capacity

半刚性构架的结构响应随刚度变化因子的变化见图13，分析发现节点刚度对腹杆的受力基本无影响，弦杆的轴力响应随着刚度的增大而减小，其中柱中弦杆较梁中弦杆趋势更明显。随着节点刚度的增加，构架承载力呈非线性增加，见图14，图14中破坏荷载比例系数是指半刚性构架的承载力和刚性构架的承载力的比值，破坏荷载比例系数随着刚度变化因子呈非线性增加，通过非线性拟合，变化关系为：

(2)

4 结 论

为了特高压1 000 kV出线构架的节点半刚性设计，本文开展了节点半刚性非线性分析及其对构架力学性能的影响研究。得出如下结论:

1)通过数值仿真重现了节点试验，数值仿真从受力变形特点上符合试验结果，验证了数值模型的正确性。

2)研究了各类节点的破坏机理并获得了弯矩-转角曲线。其中C型插板连接节点以螺栓剪坏，T型和十字型插板连接节点以插板弯曲破坏为控制条件。初始刚度主要与插板螺栓数量相关，承载力主要与插板形式相关。

3)将弯矩-转角曲线应用到连接单元，建立基于半刚性的出线构架模型，对比了半刚性构架和刚性构架在设计荷载下和极限荷载下的结构响应，发现设计荷载下半刚性构架的杆件最大轴力比刚性构架大10.9%，刚性构架的极限承载力是半刚性构架的2.3倍；随着节点刚度的增加，构架极限承载力呈非线性增加。