小流域淤地坝溢洪道压强特性分析及挑流消能计算

刘 荣

(甘肃省张掖市甘州区安阳水利管理所，甘肃 张掖 734000)

小流域淤泥坝溢洪道的布置是整个水利工程中的重要环节，同时也是保证水利工程安全和综合效益最大的关键[1]。在以往的水利工程中，随着下游泄水的流速越来越大，直接影响泄水消能系统的安全。因此，安全泄洪是水利枢纽设计中的重要问题。在水利工程中，为了消除高速水流的巨大能量，主要利用光滑溢洪道或溢流坝进行挑流消能，但溢流面容易遭到空蚀破坏，需要加强对溢流面的局部不平整的要求[2- 4]。另外在泄水建筑物中，泄洪道作为水利工程中常见的建筑物，工程中主要建筑的安全与其泄洪能力和安全运行息息相关，在现今的水电工程规模日益增巨的情况下，泄洪在整个水利工程中的越来越重要。

在上述情况下，建筑物需要尽可能减小泄流宽度，以至于增加了单宽流量，最终使流过泄水建筑物的水流具有巨大的动能，若没有合适的消能设施，将严重破坏河床，引起河床的冲刷，严重威胁坝址安全[4- 6]。所以在泄洪时，消能的任务很艰巨。

通过分析小流域溢洪道压强特性以及计算挑流消能，合理消散能量。传统的小流域淤泥坝溢洪道压强特性分析及挑流消能计算方法中存在灵敏度低的问题，导致挑流消能计算的不确定性风险过高。因此提出小流域淤泥坝溢洪道压强特性分析及挑流消能计算方法，解决传统的方法存在的问题。

1 流域淤地坝溢洪道压强特性分析

1.1 建立溢洪道三维模型

依据地理资料绘制出小流域淤泥坝下游的三维模型，模拟溢洪道的水流状态。如图1所示。

图1 淤泥坝溢洪道三维模型

建立三维模型主要使用CAD软件，以某一实际淤泥坝溢洪道为例，使下游水流稳定，陡坡段末端接100m水平面，坝上游接100m×80m的水平面，在此基础上，建立模型。图形范围为库区长100m，宽80m，模型高度均为7m。将CAD建好的几何模型导入至GAMBIT中，选择适当的求解器，给定水面位置，划分网格。根据实际求解情况制定边界条件的类型，最后，将生成的mesh文件导入FLIENT中，设置相关参数[7]。为后续溢洪道压强特性分析做准备。

想要溢洪道压强特性需要在模型空间区域上进行大量计算，其前提就是使用网格[8]。网格的质量对计算精度和计算效率有重要影响。网格质量越好，计算精度和效率越快。在图1的三维模型基础上，用六面体结构网格单元划分网格，并设置边界条件，使用FLUENT软件模拟计算对淤泥坝溢洪道的水流流场，完成以上步骤后，分析小流域溢洪道压强特性。

1.2 溢洪道压强分布及计算

对于小流域淤泥坝溢洪道的压强特性分析，压强场的计算是水流数值求解的一个特殊问题，目前没有可直接求解压强的方程，对可压缩流体，可将其质量视作连续方程中的独立变量进行求解，再根据水流质点的微分方程求出压强[9]。

水流质点在作曲线运动时受到离心惯性力的作用，如图2所示。

图2 顶流体微分柱受力图

重力沿y轴方向相反的方向为离心惯性力的方向。取y轴坐标原点于顶端，方向向上，列出图中的所示的方向的微分方程：

(1)

式中，p—底部压强；s—底部面积；y—y轴距离；v—流速；r—曲率半径。以上表示的是压强分布，利用断面水流能量方程计算溢洪道顶端上面任一点压强值[10]。断面水流能量方程如下：

(2)

当G1=0时，则上式为：

(3)

将公式(3)带入公式(1)中，得到：

(4)

式中，G0—溢洪道顶端水头；G1—顶端高度；χ—流速水头系数；∑g—从管道口到压强测点断面的总水头损失[11]。利用公式(3)可计算出顶端的最大负压值，利用公式(4)可计算出溢洪道管道断面上任一点压强值，通过计算的最大负压值和压强值，实现小流域淤泥坝溢洪道压强特性分析。

2 小流域淤泥坝溢洪道挑流消能计算

以溢洪道为研究对象，计算挑流消能。在初始溢流阶段，没有能量损失，势能完全转化为动能，水舌的流速为：

(5)

式中，g—重力加速度；D—上下游水面差；Q—水面高程差。由于水自身的黏滞性、溢流过程中掺气的情况、溢流面的糙率和空气阻力等原因，都会引起水头的损失[12]。因此引入修正系数来修正流速：

(6)

(7)

式中，ξ—修正系数；T—单宽流量。水流在正常流通的情况下，由于空气阻力的作用，损失一部分能量，引入空气阻力修正系数，则考虑因空气阻力能量损失，入水速度为：

(8)

式中，δ—空气阻力修正系数；τ—中间变量，与挑角差相关，挑角差越大τ越小，挑角差越小τ越大，出于工程安全考虑，设置τ的取值范围在0.9～1之间。在公式(8)中，空气阻力修正系数的取值与射流与空气接触的面积以及射流流速相关，若空气中受到的空气浮力越大，说明水流掺气率越高，且滞空时间越长，能量损失越多[13]。因此，修正系数的取值范围还与挑角差相关。由于影响因素较多，在公式(8)中，根据修正系数与水面高程差成反比关系来初步确定空气阻力修正系数的取值，水面高程差越大修正系数越接近下限，正常情况下，空气阻力修正系数取值范围为0.7～1。

水舌进入下游后，冲刷下游河床，形成冲坑。同时与冲坑中静水相互扰动，使大部分能量在此过程中损失，剩余能量变为尾水动能。根据能量守恒方程计算能量损失：

(9)

式中，△E—冲坑内损失的能量[14]。通过计算损失能量，计算在单宽水流的泄洪功率和损失能量在总能量的比例：

(10)

利用公式(10)计算出水体耗散功率：

E1=9.5T△E

(11)

从二元水跃的消能率出发，可以推得水体的单位体积消能率为：

(12)

式中，T—单宽流量；D—上下游水面差；E0—单宽水流的泄洪功率；p—损失能量在总能量的比；E1—水体耗散功率；f—比例系数，该值随着单宽流量的减小或随着上下游水面差的增大而增大的趋势；φ—单位体积消能率[15]。从上述过程可知，消耗△E所需的水体体积为：

(13)

根据二元水流冲坑的几何形状计算冲坑深度，由于二元水流的剖面形式基本上接近抛物线，因此可以得到冲坑深度为：

(14)

式中，d—水垫深度。通过上述过程得到冲坑净深。至此，小流域淤泥坝溢洪道挑流消能计算完成。

3 仿真实验分析

在小流域淤泥坝溢洪道压强特性分析及挑流消能计算方法仿真实验中，以灵敏度为衡量参数，对比不同方法的优劣性，依据实验要求，采用模型实验。

3.1 实验准备

根据仿真实验的实际需求和模型实验的相似理论，实验采用整体正态模型，按照重力相似准则设计模型参数。具体参数设计见表1。

表1 实验模型主要参数

在实验中使用的主要量测仪器有针对水位、水深测量的测针，误差在0.1mm。水面线的量测采用水准仪，流速测量采用微型旋浆流速仪，流速仪采样时间为15s，采样间隔时间为60s，平均采集5次，求出平均值作为该点的流速值，流速仪起动流速为2.0～3.0cm/s。

在以上设定下，分别进行10次和100次的模拟溢洪道泄洪冲击过程，根据洪水过程的不确定性，计算挑流风险，进而分析不同方法的灵敏度。

3.2 灵敏度实验结果及分析

在灵敏度分析中将不确定因素作为随机变量，然后利用MATLAB软件，计算挑流消能风险值，根据风险值分析不同方法的灵敏度。其中随机变量取值见表2。

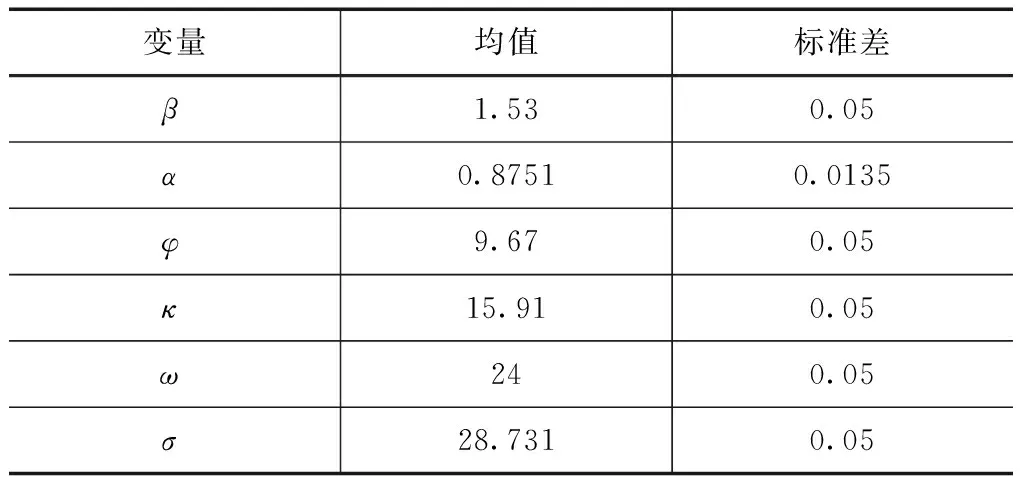
表2 随机变量取值表 单位：mL/m2

表2中β表示洪峰消减系数、α表示冲抗系数、φ表示坎高、κ表示坎宽、ω表示挑角，σ表示反弧半径。以上即为不同方法中灵敏度分析中的随机变量。实验结果如图3所示。

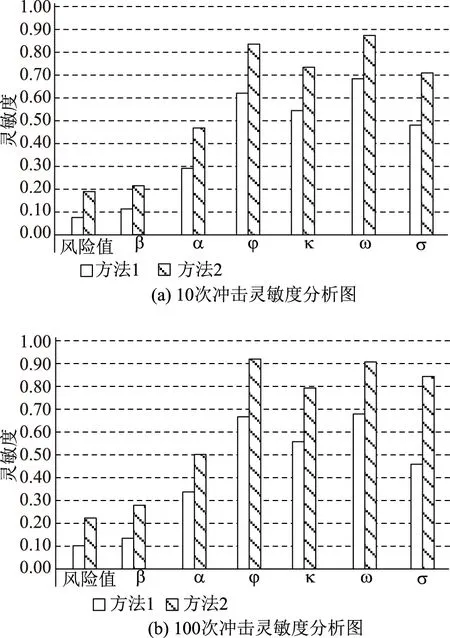
图3 不同方法灵敏度实验结果

图3中方法1是传统的计算方法，方法2是提出的小流域淤泥坝溢洪道压强特性分析及挑流消能计算方法。图3(a)中结果显示，方法1的的各项随机变量以及风险值的灵敏度均低于方法2的灵敏度，经过计算得出方法1平均灵敏度为0.4086，方法2平均灵敏度为0.6271；图3(b)中显示结果类似，方法1的各项随机变量以及风险值的灵敏度均同样低于方法2，经过计算，方法1平均灵敏度为0.4607，方法2平均灵敏度为0.6793。

综上所述，在两次实验中，方法2的平均灵敏度均高于方法1的平均灵敏度，说明提出的小流域淤泥坝溢洪道压强特性分析及挑流消能计算方法优于传统方法。

4 结语

水利工程中为了消除高速水流的巨大能量，长期以来利用溢洪道进行挑流消能，绝大多数运行良好，发挥了巨大作用，但是依然存在大坝失事的情况。研究小流域淤泥坝溢洪道压强特性分析及挑流消能计算有一定的现实意义。利用CAD软件建立溢洪道三维模型，利用该模型分析压强特性并实现挑流消能的计算，通过设计的对比实验证明了提出的方法有效地解决了传统方法中存在的问题。通过对小流域淤泥坝溢洪道的相关研究，结合以往的一些研究成果分析，深刻体会到研究溢洪道压强特性和挑流消能计算的意义。但是受到对三维模型设计学习的限制，有很多问题没有深入研究，以上研究中依然存在一些之处，依然需要更深入的探讨和改进。