井灌区灌溉可应用机井的空间布局优化探究

滕 凯

(海城市水利事务服务中心，辽宁 海城 114200)

如何在某特定区域内合理部署若干灌溉机井，系为机井空间布局优化计算的重点环节所在。一般此类问题的研究方法主要有三种，一是多边形格网法，二是电荷排斥模拟方法，三是优化算法结合一定准则(目的函数)法。因为井灌区存在机井限建区，而且是典型的非规则多边形区域，倘若选用第一种方法，则通常无法保证井数实现均匀分布；而第二种方法还未付诸于实践，与其相关的文献资料相对比较匮乏；只有第三种方法不仅理论基础夯实，而且在物流配送、村镇土地空间布局等多领域均实现了广泛应用。所以本研究决定重点通过此方法来实现合理布局机井的计算和设计目的，确定案例区域相对优化的布井数量与区域机井分布状态，以为区域灌溉机井的空间布局工程应用提供计算技术参考。

1 研究区概况

本文案例对象系位于华北某县的覆盖2镇12村的井灌区。经实地勘察与资料查询后得知，该区域系为典型的平原地区，西北部地势偏高，东南部地势偏低，海拔差不是很大。水文地质系为第四系地质，主要以灰岩为主，其间岩石裂断带和裂缝发育，有利于地下水潜藏。区域位于暖温带，属半湿润大陆性季风气候区，四季分明，雨热同期，春季少雨干燥，夏季多雨高温，秋季凉爽依然，冬季低温少雪。该区域机井现状具体见表1。

本区已投入使用的机井均由当地村民出资建设，由于规划不得当，致使机井分布欠缺合理，一些区域在农忙时时常出现达不到预期要求出水量问

表1 井灌区机井现状基本统计表(眼)

题，该情况的出现不仅延误作物灌溉最佳时机，还不利于庄稼正常生长，直至最终形成减产甚至无产的局面。

井灌区灌溉可应用机井密度统计分布状态如图1所示。

图1数据揭示，该区灌溉密度基本保持在0.9眼/hm2左右，通过倒数推算求解发现，单井需灌溉10.92hm2土地，远高于当前的3.59hm2。很明

图1 井灌区灌溉可应用机井密度统计分布状态图

图2 可应用类井灌区机井灌溉率统计分布状态图

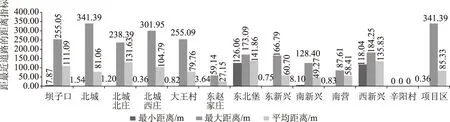
图3 基于近路距离的可应用类井灌区机井统计分布状态图

显，该区的机井数量不充足，单井灌溉能力己无法切实满足当前农业需求。

区域可应用类井灌区机井灌溉率统计分布状态如图2所示。

图2数据揭示，区域机井分布过于集中的系数北城村，如果现存机井达到了使用期限而不得不报废时，局部可选择的部署空间也相对狭小。虽然其他村落的灌溉率差强人意，机井建设也存在很多问题，但却为新井建设预留出了足够大的空间。所以，唯有各村重新优化机井布局方案，才能提高地下水资源的使用率，延迟机井的使用期限。

基于近路距离的可应用类井灌区机井统计分布状态如图3所示。

图3数据揭示，整个井灌区的各行政村的指标数据均存在较大差异，该区的机井灌溉便捷性不够。造成此现象的原因：一是道路建设不完善；二是井位选取位置不当，与道路间隔太远。

综上可知，当前井灌区存在多重问题，最突出的是机井量少、机井远离道路、井距不合理，由此引发了出水量少、灌溉延迟、地下水利用率过低等问题。就本质上看，导致这些问题发生的根源是机井布局缺乏统一规划，而且布设随意性较强。通过实地勘察还发现，研究区的机井建设全由村里人出资，以农户自打水井为主，并且村民节水观念不强，忽略了地下水资源的循环使用。所以，要站在新的视角上来部署新井，在提高地下水使用率，合理使用现状机井，充分考虑现实场景及实际需求的基础上，通过新建井数的科学计算确定出最理想部署方案。

2 构建优化模型

机井标识通常借助两要素：一是地理空间坐标，二是属性值。倘若盲目地调整机井位置，必然会使原有井群布局发生变化，也就不能保证农业灌溉的及时性与便捷性。因此，机井布局的空间有关性是极其重要的，而这就牵扯到了空间抽样理论的应用。该理论是围绕如何分布样本点展开相关研究的，也就是采用优化算法，从有限的样本点集中，随机抽取某一子集，使其通过优化处理达到预期要求。很明显，这是一类组合优化问题，可利用下式表达数学模型：

minf(x)

s.t.g(x)≥0

x∈D

式中，D—样本点集；X—决策变量；g(x)—约束函数；f(x)—优化准则目的函数。所以，可利用该模型对机井空间布局这一复杂问题进行简化处理。具体来讲就是先抽取出与井数等量的点，再按照限定准则及实际要求进行优化处理，最后确定出最符合要求的的新建井点。

2.1 主要决策变量

2.2 优化基本准则

机井合理布局不仅能延长机井使用期限，还能提高地下水使用率，形成良好灌溉效益。因此，井群分布一定要合理、均匀。由于现状机井仍能正常使用，解决农业灌溉问题，所以优化准则的制定与实施务必要与当前机井的布局要求相吻合。

在应用的样本优化选取准则中，平均最短距离最小化准则(MMSD)最大优势在于能尽可能地均匀分布采样点，使任意点与其最邻近点的间距达到最小值。

所以，本研究选取MMSD当作机井布局优化目的，其优化机理为：研究区内某宜布井点与其最邻近的新建井点、现用井点间的距离的期望最小值，其计算公式具体如下：

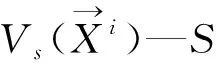
2.3 重点约束条件

(1)井距必要限制：为避免机井同时运作时会互相影响，因此要将新建井点与其最邻近井点的间隔距离控制在27502m以上。

(2)井数必要限制：由前文表数据可知，机井数量可切实满足灌水需求，但要消除一切不利灌溉因素。

(3)优先等级限制：优先选取一级宜布井点，在条件达不到的情况下，再考虑其他级别的宜布井点。通过实地勘察与数据统计发现，一、二、三级可部署的井点总量分别为12125、19051、9333个。

3 优化算法与优化布局结果

3.1 选取优化算法

启发式算法是当前颇受业界人士推崇与青睐的一种优化技术，在空间优化布局问题的解决上具有无与伦比的优势。当前，使用较为广泛的空间布局优化方法有很多种，比如遗传算法(geneticalgorithms，GA)、模拟退火算法(simulatedannealing，SA)等。对这几种算法的优缺点进行全面分析后发现，SA的优势更为突出，具体表现为并行搜索能力强、操作便捷、适用范围广、受条件限制少。因此，可将此算法应用于本课题研究中，以达到空间优化的目的。

充分利用SA算法优势的基础上，结合空间信息的特征，利用Hmax对采样点的移动空间进行科学界定，以保证经优化处理后的各采样点均处于最佳部位。Hmax一般被视为相距最远的两个点的距离，这样就能为样点移动预留出足够的空间，从而移动到最理想部位。该算法的运行过程具体如下：

Step1：循环频次n，起始温度为t；

Step2：计算目的函数φ(S0)，随机选取一个样本S0。同时通过特定的随机扰动，计算目的函数φ(S1)，生成新样本S1。决定是否接受新样本主要参考Metropolis准则。

Pc(S0→S1)=

其中，Pc(S0→S1)表示S0替换以S1的概率；

Step3：第2步循环频次到达n次，实施温降过程：t=c·t，c∈(0，1)并且近似等于1；

Step4：设置最低温度tmin，重复前3个步骤，算法在t≤tmin时终止，输出样本S0。

3.2 布局优化结果

MATLAB是最近推出的一款主流计算软件，相较于传统的C语言和FORTRAN语言，它的功能更强大、优势更突出，现在被广泛应用于空间布局优化问题求解领域。因此，在本研究中，笔者利用MATLAB软件确定出了机井布局优化模型的最优解，也就是新建井点的地理坐标，然后将求取的坐标数据完整、准确地导入ArcGIS中，由此便可生成如图4所示的井灌区机井空间优化布局结果图。而井灌区现状可应用类机井空间分布状态图具体可见图5所示。

图4 井灌区优化后的机井空间分布状态图

图5 井灌区现状可应用类机井空间分布状态图

图4优化后的机井空间分布状态揭示，新建井点合理地部署在井灌区内，即便这些井泵同时处于工作状态，也不会产生任何不利影响，由此一来，既提高了水资源利用率，还保证了灌溉的及时性与便捷性。整体来看，新建井点基本靠近道路，简化了灌溉操作的复杂性，而且处于一级宜布井点区域，也就意味着可忽略二、三级宜布井点。

总而言之，研究区机井空间优化布局结果可满足现实灌溉需求，也就间接证实了笔者采用的优化布局方法是完全可行的。首先，通过网格单元划分确定出具体井数，既能解决整体灌区不均匀的难题，还能保证各单元的农作物得到及时灌溉；其次，适宜性评价为井位选取划分了等级，通过等级划分合理控制了选取范围，简化了中间环节，提高了布井效率；最后，利用优化布井法选取了最佳井点，有效缩短了布设时间。

4 结语

(1)调查分析了案例井灌区现状可应用类机井的空间分布状态。

(2)基于主要决策变量、优化基本准则以及重点约束条件，构建了案例井灌区灌溉机井空间优化分布数理计算模型。

(3)基于优化算法计算给出了案例井灌区优化后的灌溉机井空间分布计算成果。虽然不同灌区的区域条件及现存机井分布状态千差万别，但本研究的计算实现样式，可为各井灌区灌溉机井的空间布局优化设计及工程应用提供技术参考。