不同动应力比下加筋前后砾性土的动三轴试验分析

王家全，畅振超，王 晴，唐 毅

(广西科技大学土木建筑工程学院，广西 柳州 545006)

采用土工格栅对坝顶区域进行加固是一种有效的高土石坝抗震加固措施，其可以提高坝顶土体结构的稳定性，减小土体侧向变形，改善堆石料的力学和变形特性，且施工简便，具有较好的经济效益。砾性土具有良好的力学性能和透水性能，被广泛应用于水利工程中。加筋前后堆石料等粗粒土的受力及变形特性均可用静动三轴试验进行研究。目前，有关加筋粗粒土静力特性方面，已经有众多学者进行了研究，并取得了丰硕的成果[1-5]。在堆石料等粗粒土动力特性方面，刘汉龙等[6]研究发现加筋后堆石料的残余变形变小，且随加筋层数增加残余变形减小的越明显；何亮等[7]研究了加筋前后堆石料残余变形的变化规律，得出堆石料残余变形随围压和动应力比的增大而增大，堆石料残余变形的减小幅度随加筋层数的增加而逐渐降低；Fu等[8]利用大型动三轴仪研究了碎石填料在循环荷载下的残余应变随振次的变化规律，并建立了考虑残余应变影响的经验模型；Madhavi等[9]对加筋砂土进行了大型动三轴试验，结果表明低围压下动模量不会随加筋层数的增加而改变，但在高围压下随着加筋层数的增加动模量显著增大；Jin等[10]研究了密实度对尾矿砂动孔隙水压力的影响，认为密实尾矿砂在频率和振幅减小时，动孔隙水压力的增长速率会随之减小。

综上所述，目前关于加筋粗粒土静力特性的研究已经较为深入，粗粒土动力特性方面也有学者进行了相关研究，但大部分研究对象为碎石土填料等，关于砾性土填料在加筋前后动力特性变化规律的研究还鲜有报道。本文采用双向土工格栅作为加筋材料，选用直径150 mm、高300 mm的大尺寸试样来开展循环荷载作用下加筋砾性土的动三轴试验。对比分析不同动应力比下加筋前后砾性土试样轴向累积应变、回弹模量和动孔隙水压力等动力特性的变化规律，揭示不同动应力比下筋材对砾性土动力特性的影响。试验结果可为加筋土工程的设计施工提供参考，为控制减小加筋土结构沉降变形提供理论依据。

1 试验装置及试验内容

1.1 试验材料

试验用土为广西柳州河砂，由颗粒分析试验结果可知，颗粒粒径范围为d=0.5～10 mm，不均匀系数Cu=5，曲率系数Cc=1.25，依据《土工试验规程》[11]可判定为级配良好的砾砂，颗粒级配曲线如图1所示。试样为直径D=150 mm、高H=300 mm的大尺寸圆柱形试样。土样的最大粒径与试样直径的比值为1/15，可以忽略尺寸效应对试验结果的影响[11-12]。筋材为双向塑料土工格栅，格栅网孔尺寸为20 mm×20 mm，纵向拉伸屈服力为18.6 kN/m，横向拉伸屈服力为15.4 kN/m，试样布筋方式如图2、3所示，采用分3层等间距平铺布筋。

图1 砾砂颗粒级配曲线

图2 塑料土工格栅

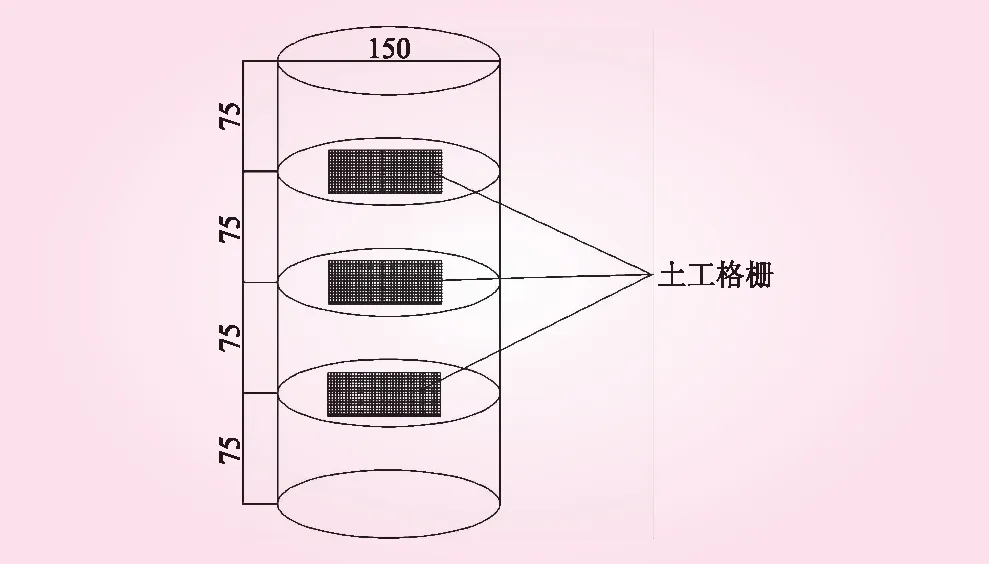
图3 筋材铺设示意(单位：mm)

1.2 试验设备

本试验采用GDS电机控制式动态三轴测试系统来进行动三轴试验。该系统由驱动装置和压力室罩、围压和反压控制器、孔压传感器、DCS数字控制系统等模块组成，如图4所示。系统的基本技术指标为最大轴向力为10 kN，最大围压与反压均为2 MPa，循环荷载频率范围为0～5 Hz，轴向位移冲程±50 mm。

图4 GDS电机控制式动态三轴测试系统

1.3 试验方案

试验采用单一幅值循环加载；试验类型为固结不排水试验，固结类型为等向固结；循环荷载的控制类型为应力控制；加载频率为1 Hz，加载波形选用如图5所示的半正弦波。

图5 加载波形

本试验共设置6组工况，对围压为90 kPa时，不同动应力比下的饱和砾性土进行加筋与无筋砾性土动三轴试验。从各动力参数曲线变化趋势和加筋效果系数两方面，对比分析不同动应力比下饱和砾性土在加筋前后轴向累积应变、回弹模量、动孔隙水压力等动力特性的变化规律；并对不同动应力比下试样的轴向累积应变与振次关系进行拟合，再对拟合参数进行对比分析，试验控制条件和参数见表1。

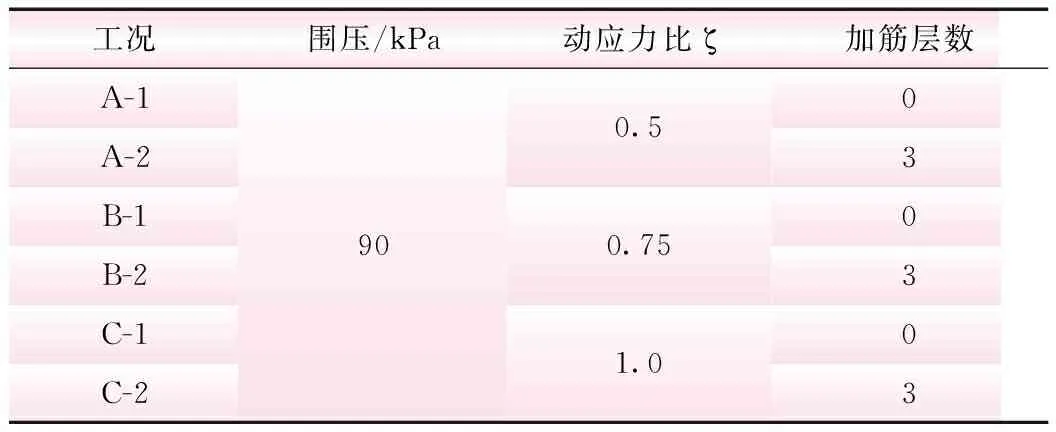
表1 试验控制条件和参数

2 试验结果与分析

2.1 加筋前后砾性土动力特性对比分析

2.1.1对砾性土轴向累积应变的影响

不同动应力比下，加筋前后砾性土轴向累积应变与振次关系曲线如图6所示，其变化趋势均为骤增→略增→稳定。前200个循环内，轴向累积应变均急剧增大，振次N=200～1 500次时，轴向累积应变的增长速率逐渐削减，曲线的斜率逐渐减小，振次N=1 500次之后，轴向累积应变的增长速率逐渐趋近于0，曲线逐渐趋于平缓。由图6可知，随着动应力比的增大，轴向累积应变会随之增大。因此，工程中应尽可能的控制动应力比，从而有效控制加筋土结构在循环荷载下的长期累积变形。

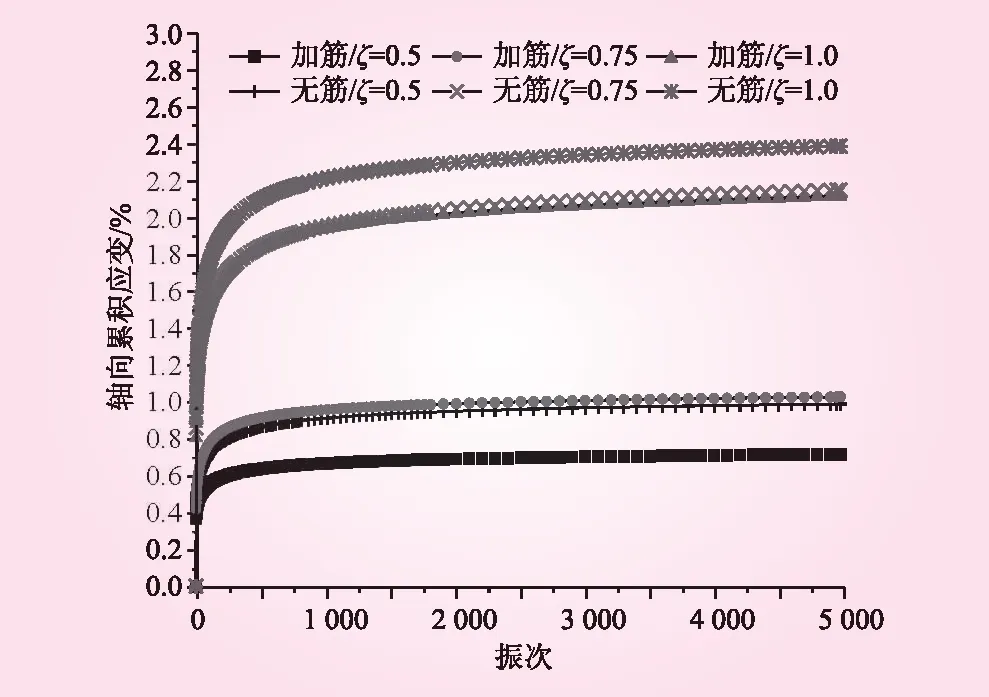
图6 不同动应力比下轴向累积应变与振次关系曲线

由图6可知，加筋试样的轴向累积应变与振次关系曲线均位于无筋试样对应曲线的下方，说明不同动应力比下加筋后试样的轴向累积应变均有减小，即不同动应力比下加筋均具有减小砾性土轴向累积应变的作用。从加筋前后轴向累积应变与振次关系曲线间的距离可知，当动应力比ζ=0.75时，曲线间的距离明显大于动应力比为0.5和1.0时，说明加筋对轴向累积应变的减小作用受动应力比影响，动应力比从小变大过程中存在一个最优动应力比，此动应力比下加筋对砾性土轴向累积应变的影响最为显著。

为了更加直观的描述加筋对砾性土轴向累积应变、回弹模量和动孔隙水压力的影响程度，参考文献[13]中关于加筋砂土静三轴试验的研究，引入加筋效果系数ηεd、ηEd和ηud：

(1)

(2)

(3)

式中，ηεd为轴向累积应变加筋效果系数；(εi-ε0)为加筋与无筋试样轴向累积应变最终应变差值；ε0为无筋试样轴向累积应变最终值；ηEd为回弹模量加筋效果系数；(Ei-E0)为加筋试样与无筋试样回弹模量最终模量差值；E0为无筋试样回弹模量最终值；ηud为动孔隙水压力加筋效果系数；(ui-u0)为加筋试样与无筋试样动孔隙水压力与最终孔隙水压力差值；u0为无筋试样动孔隙水压力最终值。

表2为不同动应力比下的加筋效果系数。由表2可知，各动应力比下轴向累积应变加筋效果系数均为负值，即加筋后试样的轴向累积应变均小于无筋试样。对比不同动应力比下的ηεd发现，当动应力比=0.75时，轴向累积应变加筋效果系数最小，说明该工况下土工格栅加筋对减少累积应变效果最为显著。

2.1.2对砾性土回弹模量的影响

图7为不同动应力比下加筋前后砾性土试样回弹模量与振次关系曲线。不同动应力比下回弹模量与振次关系曲线均呈现略减→递增→稳定的变化趋势。对比不同动应力比下回弹模量与振次关系曲线可知，随着动应力比的增大，加筋前后砾性土的回弹模量均会随之增大，但增长幅度略有不同；从不同动应力比下对应曲线间的距离可以发现，动应力比从0.5涨到0.75时回弹模量增长幅度较大，而动应力比从0.75涨到1.0时略有减小。

由表2可知，不同动应力比下回弹模量加筋效果系数均为正值，表明加筋后的试样回弹模量相比于无筋试样均有所增大，也就说明加筋可以提高砾性土的回弹模量。随着动应力比的增大回弹模量加筋效果系数随之增大，但各系数间的差值为0.017、0.003，说明随着动应力比的增大，加筋对砾性土的回弹模量影响逐渐增大，但影响程度逐渐减小。与表2中轴向累积应变效果系数和动孔隙水压力效果系数相比，回弹模量加筋效果系数均较小，说明不同动应力比下，加筋对砾性土回弹模量的影响较小。

2.1.3对砾性土动孔隙水压力的影响

不同动应力比下加筋前后砾性土试样动孔隙水压力与振次关系曲线如图8所示。由图8可知，不同工况下动孔隙水压力与振次关系曲线的变化趋势基本相同，在振次N=200次以内的振动初期，动孔隙水压力会随着循环荷载的突然施加而迅速增大，振次N=200～1 500次时，动孔隙水压力的增长速率会逐渐减小，待振次N=1 500次以后，曲线逐渐趋于平缓，动孔隙水压力逐渐趋于稳定。对比不同动应力比下的动孔隙水压力曲线发现，对于无筋试样随着动应力比的增大，动孔隙水压力会随之减小，而加筋砾性土试样的动孔隙水压力曲线基本重叠在一起，说明加筋试样的动孔隙水压力受动应力比的影响较小。

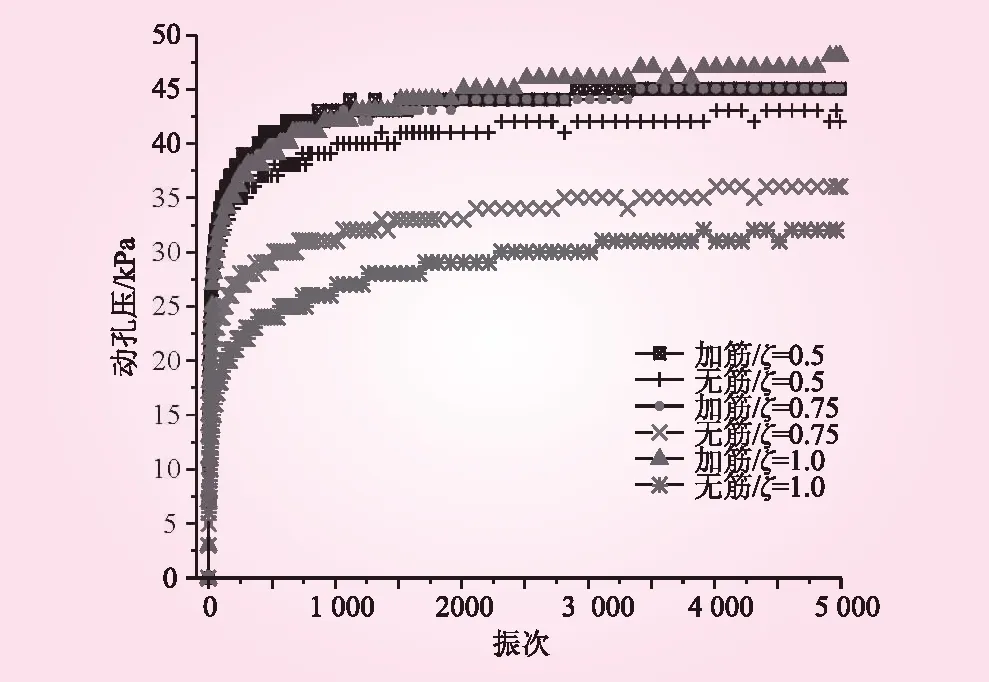
图8 不同动应力比下动孔隙水压力与振次关系曲线

由表2可知，不同动应力比下的动孔隙水压力加筋效果系数均为正值，表明加筋会使砾性土的动孔隙水压力升高，这不利于土体的承载与稳定。随着动应力比的增大，动孔隙水压力加筋效果系数随之增大，说明动应力比对无筋试样动孔隙水压力的影响会随之增大；各系数之间的差值为0.179、0.25，说明随着动应力比的增大，动应力比对无筋试样动孔隙水压力的影响程度逐渐增大。因此，在加筋土工程中应考虑加筋作用和动应力比对动孔隙水压力的影响，避免动应力比增大使孔隙水压力升高，导致土体承载能力和稳定性降低的情况发生。

2.2 轴向累积应变拟合参数对比分析

加筋前后砾性土轴向累积应变与振次的关系可以拟合为

(4)

式中，εd为轴向累积应变；N为振次；a、b、c为拟合参数。

对不同动应力比下，砾性土轴向累积应变与振次关系曲线按式(4)进行拟合，得到如图9所示的拟合曲线，拟合曲线参数及决定系数R2如表3所示。

图9 不同动应力比下轴向累积应变与振次关系拟合曲线

表3 拟合参数及决定系数

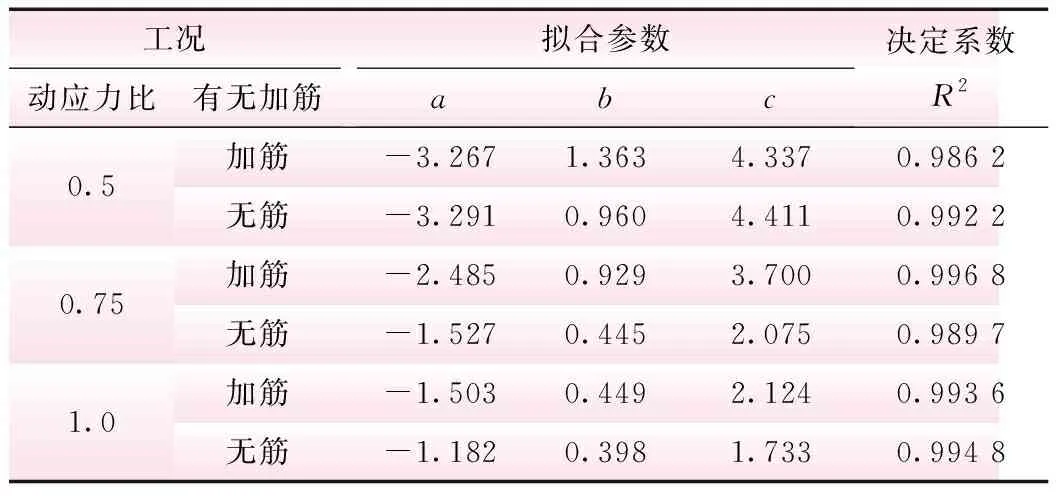
工况动应力比有无加筋拟合参数abc决定系数R20.5加筋-3.2671.3634.3370.986 2无筋-3.2910.9604.4110.992 20.75加筋-2.4850.9293.7000.996 8无筋-1.5270.4452.0750.989 71.0加筋-1.5030.4492.1240.993 6无筋-1.1820.3981.7330.994 8

由图9可知，各动应力比下的试验曲线与拟合曲线均基本重合，结合表3中决定系数R2均大于0.98，说明通过式(4)来进行拟合，其拟合效果非常好。

图10为拟合参数a、b、c与动应力比的关系曲线。由图10可知，参数a随动应力比逐渐递增且数值均为负值，参数b、c均随动应力比的增大呈减小趋势。对比加筋前后的拟合参数发现，参数a在无筋时的数值大于加筋时，而参数b、c均是加筋时的数值大于无筋时。通过以上分析可知，利用式(4)进行不同工况下轴向累积应变与振次关系的拟合，可以很好地描述加筋砾性土轴向累积应变随振次的变化规律，拟合参数的变化与动应力比的变化存在一致性，且在不同动应力比下，拟合参数a、b、c的变化规律基本相同。因此，可以通过式(4)来描述循环荷载下加筋砾性土轴向累积应变与振次之间的关系，进而通过得出的拟合公式和拟合参数来为预测砾性土填料在长期循环荷载作用下的累积沉降提供参考。

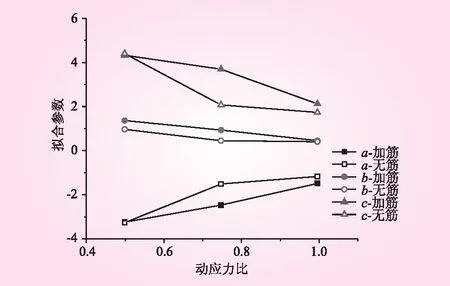
图10 拟合参数与动应力比关系曲线

3 结 论

(1)随着动应力比的增大，加筋前后砾性土轴向累积应变均随之增大；与加筋前相比，加筋后的试样轴向累积应变均有减小，说明加筋可以减小砾性土轴向累积应变的发展；加筋对砾性土轴向累积应变的减小作用受动应力比影响，随动应力比的增大存在最优动应力比，此时加筋效果最佳。

(2)各动应力比下，加筋前后砾性土试样的回弹模量均呈略减→增大→稳定的变化趋势；加筋前后试样的回弹模量均随动应力比的增大而增大，且加筋试样的回弹模量均大于无筋试样；随着动应力比的增大，加筋对砾性土的回弹模量影响逐渐增大，但影响幅度逐渐减小。

(3)不同动应力比下，动孔隙水压力与振次关系曲线均呈稳定型增长模式。随着动应力比的增大，砾性土无筋试样的动孔隙水压力减小，加筋试样动孔隙水压力变化不大。加筋后试样动孔隙水压力稳定值要大于无筋试样，且动应力比对无筋试样动孔隙水压力的影响程度随动应力比的增大而增大。

(4)对各动应力比下试样轴向累积应变与振次关系进行拟合，得到的拟合曲线与试验曲线基本重合，其决定系数R2均大于0.98，说明拟合效果非常好，拟合公式和拟合参数可为预测加筋砾性土填料在长期循环荷载作用下的累积沉降提供参考。