基于文化基因算法的梯级电站负荷分配研究

魏 勤，陈仕军，3，黄炜斌，杨会刚，马光文

(1.四川大学水利水电学院，四川 成都 610065；2.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065；3.四川大学商学院，四川 成都 610065；4.大唐四川集控中心，四川 成都 610031)

0 引 言

随着我国水电开发的不断深入，复杂多样的电站运行条件给我国电力系统运行和安全生产带来了一系列问题和挑战。电网单独制定下达负荷计划给各电厂的模式，无法充分考虑梯级上下游的水力衔接而易导致水资源浪费、电站闸门调节频繁等问题，不利于梯级的安全经济调度，而将梯级电站作为一个调度单元，由电网对梯级电站下达日内总负荷过程，由梯级电站自行调度分配的一体化运行模式可以充分发挥梯级电站协调调度的优势，提高电力调度工作效率，优化上下游负荷匹配关系。为了实现梯级电站的一体化调度运行，本文研究了梯级电站对下达总负荷的优化分配算法。

目前，国内外对梯级电站负荷分配问题的求解的基本方法主要是利用粒子群算法、蚁群算法、差分进化算法等全局启发式搜索算法，并且从提高算法的收敛速度和搜索精度、避免陷入局部最优等方向对算法进行了大量的改进优化研究[1- 6]，但极少研究结合文化进化理论通过协同全局搜索和局部搜索的改进思路，因此，本文构造了一种文化基因算法(Memetic Algorithm，MA)，希望通过本文的研究提高梯级水电站负荷分配问题的求解精度，促进梯级水电站的精细化调度，同时为该类优化问题的求解提供一种新的思路和方法。

1 梯级电站厂间负荷分配模型

本文以梯级总耗水量最小为准则来求解梯级电站负荷分配问题，考虑电站厂内机组组合优化能基本避开振动区，将厂内机组虚拟为一台机组参与厂间负荷分配。

所建立模型的目标函数为

(1)

式中，W为梯级总耗水量；N为梯级电站总数；T为调度期总时段数；Qi，t为发电流量；Si，t为i电站t时段弃水流量；Δt为时段长。

所建立模型的约束条件为

负荷平衡约束

(2)

式中，Ai为i电站的出力系数；Ni，t为i电站t时段出力；Nt为t时段下达到梯级的总负荷；Hi，t为i电站t时段平均发电净水头。

水量平衡约束

(3)

式中，Vi，t为i电站t时段初的水库蓄水量；qi，t为i电站t时段来水流量。

电站出力约束

(4)

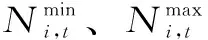
水库库容约束

(5)

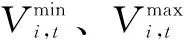
发电流量约束

(6)

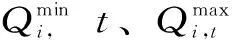
梯级水量关系约束

(7)

式中，Ii，t为i电站和i-1电站间的区间流量；τi-1为i-1电站到i电站的水流滞时。

非负约束，上述所有变量非负。

2 文化基因算法求解模型

2.1 文化基因算法框架

文化基因算法是1989年由Moscato等[7]提出的一种以文化进化过程作为启发，结合基于种群的全局搜索和基于个体的局部搜索的算法。利用种群进化算法解决给定的优化问题时，对种群的个体进行局部搜索提高个体适应度使种群整体先达到一个较好的预备状态，然后进行个体之间的相互操作实现种群进化，在进化的过程中形成了局部和全局混合的搜索机制。文化基因算法的基本框架如图1所示。

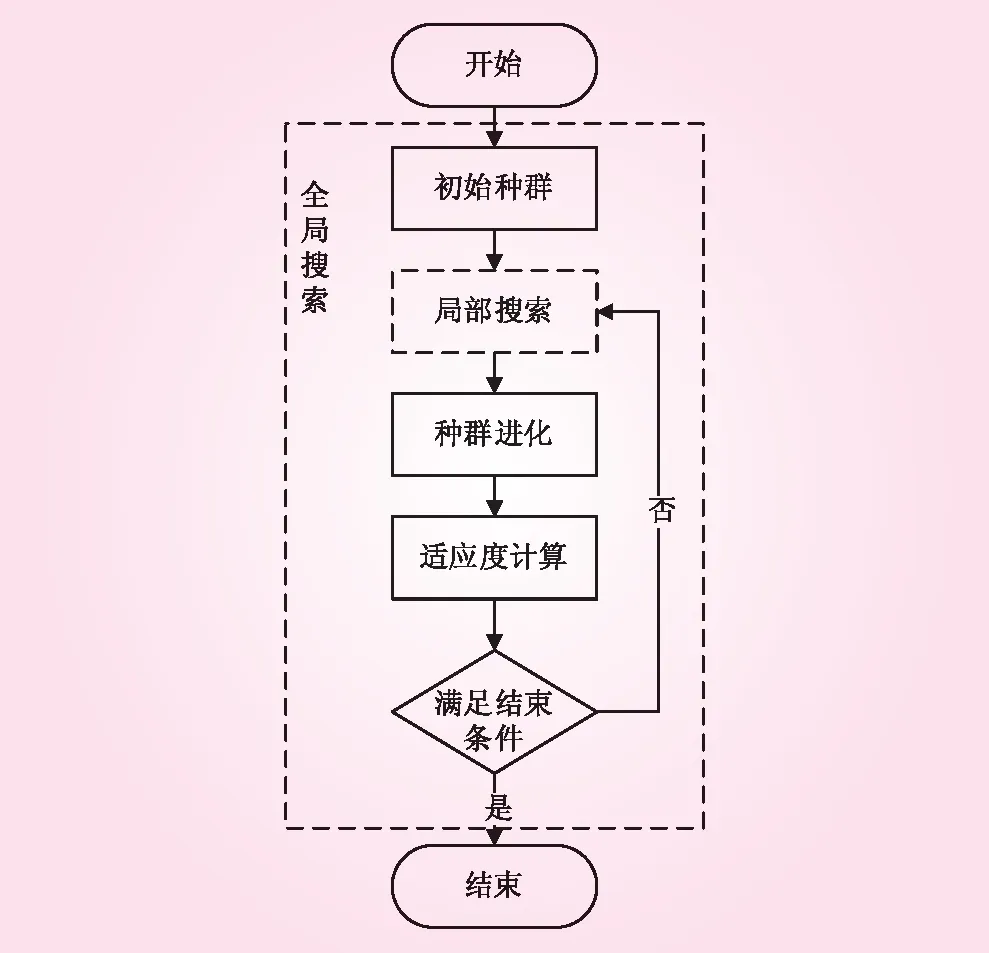
图1 文化基因算法基本流程

研究表明，在某些问题领域，这种算法结合互补机制的搜索效率比传统的遗传算法快几个数量级[8]，同时，文化基因算法提出的是一个框架，利用不同的算法作为全局搜索和局部搜索策略可以构成不同的文化基因算法[9]。基于该框架，本文研究了针对梯级电站负荷分配问题的全局搜索算法和局部搜索算法构成的协同算法。

2.2 全局搜索策略

PSO是Kennedy等[10]于1995年提出的一种模拟鸟群觅食现象的启发式进化算法。该算法具有原理简单、易于实现的优点，但存在后期进化速度较慢、易陷入局部最优的问题，为了提高文化基因算法的求解效率，本文采用了一种增加收缩因子的粒子群算法[11]。PSO中的粒子通过式(8)、(9)来更新自己的速度和位置。

vid=wvid+c1r1(pid-xid)+c2r2(pgd-xid)

(8)

xid=xid+vid

(9)

式中，w为惯性权重；c1、c2为学习因子，也称加速常数；vid为i粒子d维速度；r1、r2为[0，1]范围内的均匀随机数；xid为i粒子d维的位置；pid为i粒子的个体极值的d维位置；pgd为群体的全局极值的d维位置。

vid=k{vid+c1r1(pid-xid)+c2r2(pgd-xid)}

(10)

研究表明，该改进方法中速度限制Vmax对计算的影响可以忽略不计，所以在本研究中取为位置变化范围的最大值[12]。本文选取带收缩因子的粒子群算法(PSO-CF)作为全局搜索策略。但若对每个个体都进行局部搜索将会大量增加计算量，由于PSO算法是由全局极值作为进化方向，所以本文只对全局极值进行局部搜索以实现文化基因算法。

2.3 局部搜索策略

文化基因算法框架中的局部搜索策略本质上是基于个体的启发式算法。常用的局部搜索算法有爬山算法(Hill-Climbing，HC)、模拟退火算法(Simulated Annealing，SA)等。其中，爬山算法为一种贪心的搜索算法，从某一初始点搜索领域，将领域中的最优点作为下次迭代的初始点，直到领域中无更优解为止。而模拟退火算法在爬山法的基础上对非更优解也以一定的概率接受作为下次迭代的初始点，提高了算法跳出局部最优能力，但在爬山算法初始点位置选取较好时存在求解效率较低的问题。为了对比爬山算法和模拟退火算法作为文化基因算法的局部搜索策略的应用效果，本文分别引入以爬山法作为局部策略的文化基因算法(HPMA)和以模拟退火算法法作为局部策略的文化基因算法(SPMA)。

2.4 局部搜索激活机制

文化基因算法中引入局部搜索的目的是提高求解精度，加快算法效率，但局部搜索的频率过高会将大幅降低算法效率，因此必须限制进入局部搜索的频率。PSO算法全局极值的适应度反应了种群的进化能力，在种群进化速度较慢时引入局部搜索适应了文化基因算法的思想，本文以PSO算法全局极值前后两代适应度变幅小于一个限值作为局部搜索激活条件，考虑种群进化后期适应度变幅较小，为了避免后期反复进入局部搜索，本文设定一个自适应的局部搜索激活条件，以此限制局部搜索的频率，节约计算资源，同时提高解集质量。局部搜索激活条件为

Δfg)=fg-fg-1

(11)

(12)

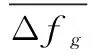
2.5 初始可行种群快速生成方法

由于梯级电站约束多且复杂，负荷分配解空间的范围难以确定、个体维度高，要保证初始种群都为可行解，完全随机的种群初始化方法会耗费大量的计算时间，为此本文提出一种基于梯级出力匹配关系的初始种群快速生成方法，如图2所示。

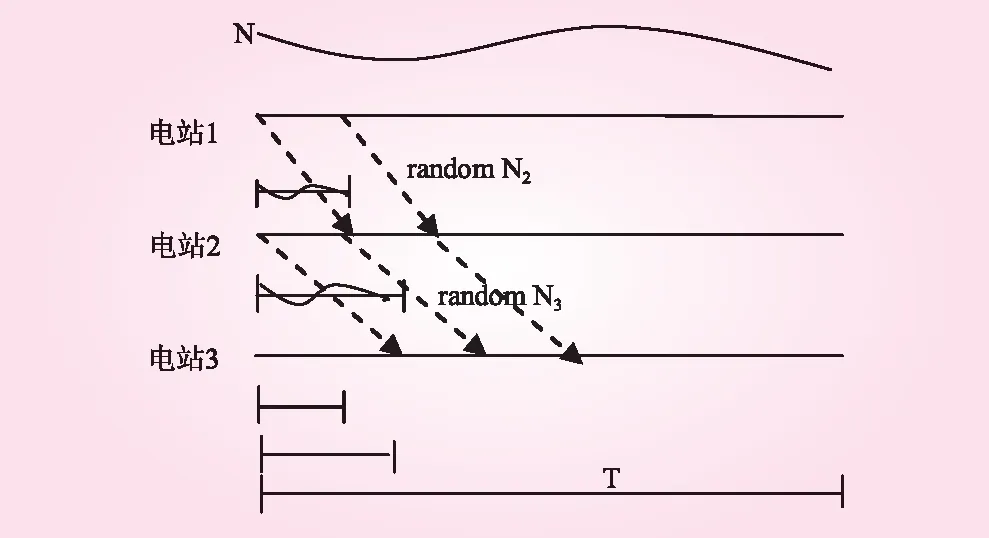
图2 初始解集快速生成方法

Ni，t=random(Ni)i=2，…，Nt∈[0，τi-1]

(13)

以电站间出力比范围内的随机值生成对应时段出力

Ni+1，t+τi=random(ε)·Ni，t

(14)

以梯级总出力反推相应时段未知出力

(15)

式中，random(x)为x在其可行范围内的纯随机值；Nall为梯级下达的总负荷；其他符号同梯级电站负荷分配模型部分。

不断重复上述过程直至生成整个调度时段所有出力过程。该方法减少了纯随机过程，同时引入了上下游出力匹配的限制，提高了初始可行解的生成效率。

2.6 算法实现

根据文化基因算法的基本框架，以PSO作为全局搜索策略，以爬山算法和模拟退火算法为全局部搜索策略分别建立HPMA、SPMA，算法流程如图3所示。

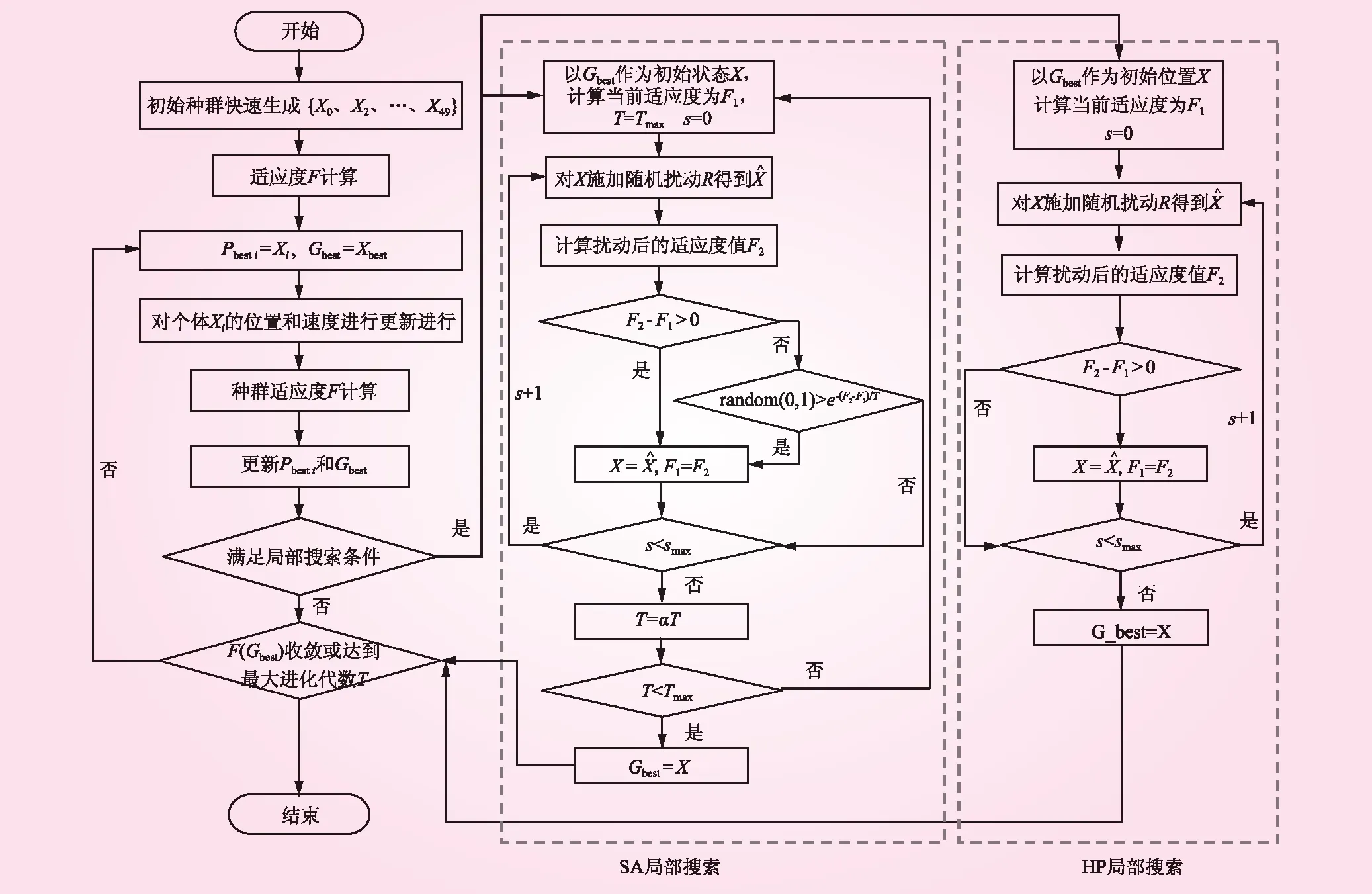
图3 MA算法流程示意

具体步骤为如下：

(1)随机生成符合约束条件的初始解作为初始粒子，本文设定初始种群数为50，得到初始种群。

(2)对初始粒子进行适应度计算，同时记录各粒子的个体极值Pbest和全局极值Gbest。本文求解模型的目标函数为梯级耗水量最小，对于不满足约束条件的粒子，直接取其适应度为0，设定适应度函数为

(16)

式中，F为适应度；W为梯级耗水量，m3。

(3)判别是否满足局部搜索激活条件，若满足则对全局极值进行局部搜索，选择爬山法为局部搜索策略则进入(4)，选择模拟退火算法为局部搜索策略则进入(5)。

(4)利用爬山法进行局部搜索的基本过程为：①以进入局部搜索的全局极值为初始状态X0；②以下式对旧状态X0施加随机扰动，产生新的状态X1；③对当前状态目标函数F计算；④基于贪心策略，若新状态优于旧状态则接受新状态，否则回复旧状态；⑤若满足搜索结束目标(达到最大迭代步数或满足精度)，则跳出局部搜索；否则回到②，继续迭代。

(5)利用模拟退火算法进行局部搜索的基本过程为：①设粒子初始温度Tmax，以进入局部搜索的全局极值为粒子初始状态X0；②以下式对旧粒子X0施加随机扰动，产生新的状态X1；③对粒子新状态X1进行目标函数F计算；④若新状态优于旧状态(优化目标为F最小)，则接受新状态，否则以一定的概率接受新状态；⑤若达到迭代步数上限则以一定规则降低温度，否则回到②；⑥若降温后温度达到最低温度Tmin，则退出循环，当前粒子状态则为局部搜索结果，否则回到②，重新开始迭代。

(6)以新的全局极值Gbest通过式(9)、(10)计算新的粒子位置。

(7)计算种群所有粒子的适应度值，记录个体极值Pbest和全局极值Gbest。

(8)判断是否达到迭代上限或全局收敛，不满足则回到(3)继续迭代，满足条件则转到(9)，本文设定迭代上限为2 500次。

(9)以全局极值作为算法的最优解，计算得到耗水量最小的梯级日运行过程。

3 实例分析

为验证该算法的合理性和可行性，本文以某梯级水电站枯期典型日的数据模拟计算梯级厂间的负荷分配情况，并与HPMA算法、SPMA算法、单独利用PSO-CF算法和SA算法求解的结果进行对比。

该梯级包括2个电站，共3个厂房。A电站为季调节水电站，B电站为日调节电站，为“一站两厂”式运行，上下游滞时取为固定值1 h，电站各项参数如表1所示。

表1 水电站综合参数

表2 计算结果对比

以实际运行的梯级总负荷作为负荷分配条件，梯级实际运行总负荷过程如图4所示。由于搜索算法都存在一定随机性，本文对4种算法分别求解5次，结果对比如表2所示，迭代过程如图5所示。

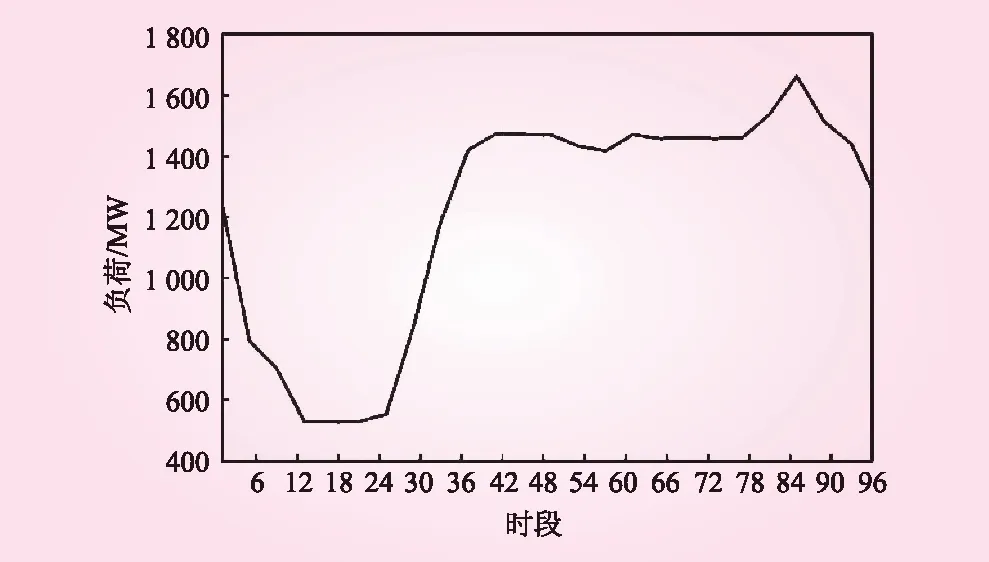
图4 梯级总负荷过程曲线

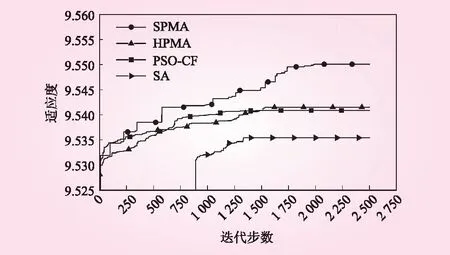
图5 迭代过程比较曲线

由表2可知，SA算法结果相对较差，明显陷入局部最优，虽然收敛速度快，但求解质量较差；PSO算法第1次和第3次结果偏离最优解较远，明显陷入了局部最优：两种MA算法各次计算结果与最优结果偏差较小，没有明显“早熟”现象，HPMA算法最终计算结果虽然都优于PSO算法，但差异较小，同时计算时间较长，求解效率较低。结合最优结果迭代过程的对比还可看出，SPMA算法在整个迭代过程的收敛速度都明显优于其他算法，具有较高的搜索精度，可得到更优的求解结果，但其计算耗时相比PSO增加了约30%。

对比4种算法得到的负荷分配过程如图6所示，可以看出4种算法中B电站小厂房都仅分配到能保证最低生态流量的负荷，而B电站小厂房机组运行水头较小，耗水率较大，分配结果符合负荷分配的基本原则，同时几种算法的求解的负荷过程差异较小，其中SPMA算法的求解结果较其他算法结果偏离相对较大，表明了SPMA算法的求解结果对负荷分配结果有较大影响，能得到更优的结果。

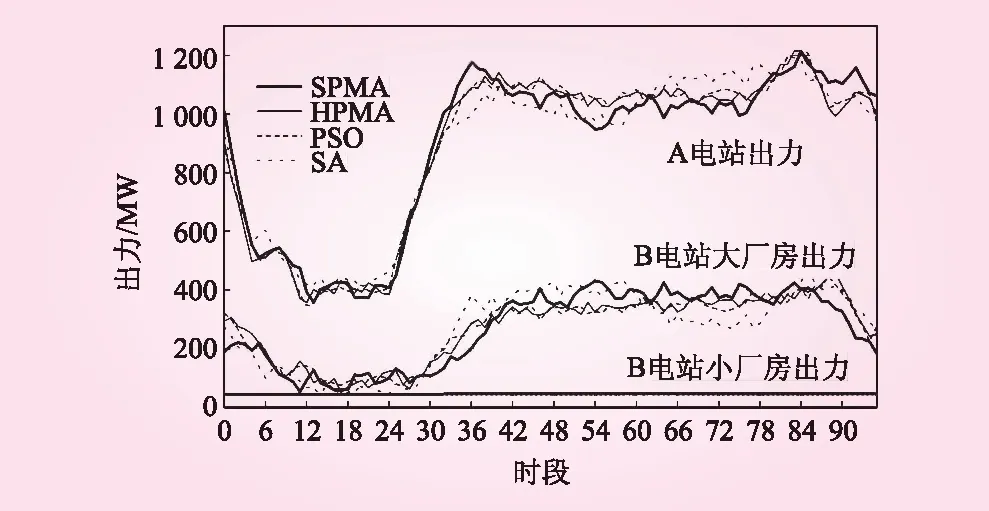
图6 电站负荷分配过程

4 结 论

本文设计的文化基因算法，在利用了粒子群算法的全局搜索能力的基础上，通过局部搜索激活机制引入局部搜索能力。采用了一种基于上下游负荷匹配关系的初始种群快速生成方法，有效的避免了梯级电站负荷问题初始可行解生成效率低的问题。实例模拟计算表明：由将PSO和SA在文化基因算法框架下组合构成的SPMA算法，在搜索精度方面较单独使用有明显提高，能有效避免陷入局部最优，有利于梯级电站水量和负荷精细化调度，对其他优化问题的求解具有一定的借鉴意义。