基于粗糙数BWM_ELECTRE方法的水库移民安置区优选
2020-07-16姚凯文
孙 瑞,姚凯文,张 丹
(华北电力大学可再生能源学院,北京 102206)
0 引 言
水库工程移民安置是一项融合社会、经济、环境等诸多因素的复杂系统工程,移民安置直接关系到工程建设的成败[1]。而移民安置工作成败的决定性因素之一就是移民安置区的选择,只有选择具有良好生产生活环境和发展潜力的移民安置区,才能保证搬迁后移民安置区社会、经济能够得到较快发展,确保实现移民安置目标。在进行移民安置区选址时,需要考虑的因素有很多,如耕地条件、基础设施条件、自然资源和社会环境等。若仅从单一因素对其进行评价,有失客观性和科学性[2],必须综合多方面因素来评判安置区的优劣。因此,建立一套科学合理且具有实用性的指标体系是十分必要的。此外,水库移民安置区的选址涉及项目业主、政府和水库移民等多方参与者,不同参与者对于移民安置区看重的条件往往不一致。因此,需要充分考虑不同决策者的决策信息。综上所述,水库移民安置区优选是涉及多个指标、多个决策者的多目标决策问题。
目前,进行移民安置区优选的主要方法有模糊综合评价法、灰色局势决策法、灰色关联决策法、模糊物元评价法、模糊层次分析法等[3- 6],本文将粗糙集理论中粗糙数的概念引入水库移民安置区优选的过程当中,采用最优最劣法(BWM)计算各项指标权重,最后通过消去与选择转换法(ELECTRE)对备选方案进行排序,建立了基于粗糙数BWM_ELECTRE方法的水库移民安置区优选模型。新的模型能够充分考虑多名决策者的决策信息,同时能够适应水库移民安置区优选的复杂性和不确定性。
1 指标体系的建立
移民安置区是移民搬迁后生产、生活的主要场所;因此,移民安置区的选择应该充分考虑该地区的生产、生活条件。此外,移民安置区还要满足移民在社会、人文、风俗习惯等方面的需要。为了对移民安置区进行科学合理的评价与选择,必须建立一套系统、科学、完整的指标体系。从移民切身利益出发,笔者选取了生产条件、基础设施、自然资源和社会环境等4个一级指标及其对应的16个二级指标构成水库移民安置区优选指标体系(见表1)。
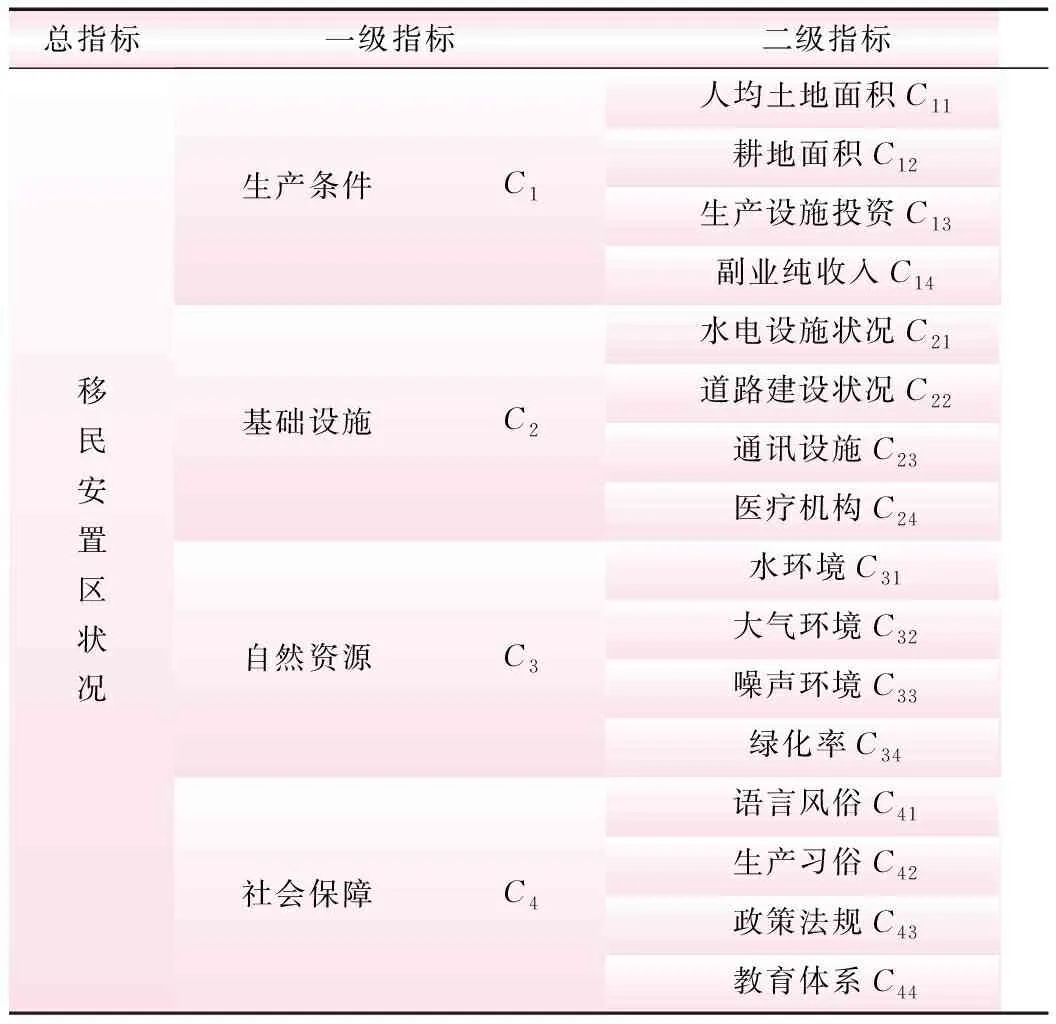
表1 水库移民安置区优选指标体系
2 粗糙数
粗糙数是新加坡学者Zhai根据粗糙集理论中的近似概念提出的一种量化专家认知的新方法,它无需效用函数、隶属函数等任何先验知识,完全依靠原始数据对多个决策者的个体认知进行整合,形成群体偏好[7]。粗糙数的构造方法如下。
定义1[8]: 设U是论域,共有n个类,表示为
R={C1,C2,…,Cn}
(1)
如果存在有序关系C1 (2) (3) Ci的粗糙数下限和上限分别为 (4) (5) Ci的粗糙数为 (6) 最优最劣法(BWM)是由荷兰学者Rezaei提出的一种决策方法[9]。与AHP类似,BWM也是基于成对比较的思想,但并不是任意两个准则相互比较,而是构造了一种结构化的比较方式[10]。通过结构化的比较方式,BWM简化了各个指标间的比较过程,从而降低了因繁琐的两两比较而导致的主观错误,其计算结果也具有更高的一致性。 这里采用基于粗糙数的BWM方法进行指标权重的计算。 (1)确定重要程度最大的最优指标CB与重要程度最小的最劣指标CW,通常由专家讨论确定。 (2)专家对所有指标相对于最优指标与最劣指标的重要程度以标度1~9进行打分,得到相应的两个比较向量 (7) (3)对比较向量进行整合,得到整合比较向量AB与AW。即 AB=(aB1,aB2,…,aBn) (8) (4)对群体信息进行集结并构造粗糙比较向量。利用粗糙数的构造方法,将整合比较向量中的元素转变为粗糙数 (9) AB=(RN(aB1),RN(aB2),…,RN(aBn)) AW=(RN(a1W),RN(a2W),…,RN(anW)) (10) 取每个粗糙序列的平均粗糙数 (11) (12) 于是得到两个粗糙比较向量 (13) (14) (5)通过数学规划求解每个指标的粗糙权重。每个指标的粗糙权重应满足 [ωB]/[ωj]=[aBj], [ωj]/[ωW]=[ajW] (15) 即 (16) (17) 求解数学规划 (18) ELETCTRE方法是多目标决策中应用广泛的一种方法,本节将粗糙数引入传统ELECTRE方法,构造基于粗糙数的ELECTRE决策方法,使其能够适应不确定性环境下的多目标决策问题。 粗糙数ELECTRE方法的具体步骤如下: (2)构造加权规范化决策矩阵。将规范化决策矩阵中每个备选方案的各指标属性值与相应粗糙权重相乘,得到加权规范化决策矩阵V=(vij)m×n。具体为 (19) 本文采用江垭水库工程作为计算实例,用基于粗糙数的BWM_ELECTRE方法进行移民安置区优选。由于江垭水库的移民安置点较多,选取其中具有代表性的三个移民安置点进行研究,分别是慈利县江垭镇的四坡村、赵家岗和临溪镇的墨园村。 通过粗糙BWM法确定各指标的粗糙权重,首先确定4个指标和每个一级指标下4个二级指标中的最优指标和最劣指标,见表2。 表2 最优指标与最劣指标 由4名专家对所有指标进行打分,得到20对比较向量,并将每个指标层面的比较向量进行整合,得到5对整合比较向量;然后将整合比较向量构造为粗糙数比较向量;最后求解数学规划,得到每个一级指标和二级指标的粗糙权重(见表3)。 表3 各指标层面下指标的粗糙权重 由此可以得到各指标的整体权重:W=([0.17,0.24],[0.13,0.19],[0.06,0.09],[0.03,0.03],[0.11,0.17],[0.07,0.12],[0.02,0.03],[0.03,0.05],[0.06,0.09],[0.03,0.05],[0.02,0.03],[0.01,0.02],[0.01,0.02],[0.01,0.01],[0.01,0.02],[0.03,0.04])。 (1)首先,根据各移民安置区的基本情况确定各项指标下的定量值(见表4)。 (2)构造规范化决策矩阵,并得到加权规范化决策矩阵。 (3)取可能度阀值p=0.6根据加权规范化决策矩阵,求得一致性矩阵C与非一致性矩阵D。 (4)进一步求得一致性优势矩阵F和非一致性优势矩阵E,以及综合优势判定矩阵H。即 (5)计算每个备选方案的效用值、遗憾值以及折衷评价值,取折衷系数ε=0.5。得,墨园村S1=0.395,R1=0.119,Q1=0.257;四坡村S2=1.903,R2=2,Q2=1.952;赵家岗S3=0.984,R3=1.092,Q3=1.039。 表4 各移民安置区的基本情况及各项指标的定量值 根据各方案折衷评价值的大小,可以得到3个备选方案的排序为:墨园村→赵家岗→四坡村,且能够看出,墨园村的综合状况优于四坡村和赵家岗,四坡村为3个备选方案中最差,而赵家岗大致居于墨园村和四坡村的中间位置。该结果与移民监测评估得到的评估结果基本一致,证实了模型的可行性和准确性。 在水库移民安置区优选的研究中,对于如何综合考虑多个决策者的决策信息的研究甚少。本文基于ELECTRE方法,引入粗糙数的概念,提出了基于粗糙数的BWM_ELECTRE方法,并将其应用于水库移民安置区优选研究中。与传统方法相比,该方法能够充分考虑多个决策者对于各指标的个体偏好。实例分析的结果表明,该方法能够得到较为准确、科学的计算结果。通过基于粗糙数的BWM_ELECTRE方法,使得进行水库移民安置区优选的过程中,能够综合考量多方参与者的决策信息,从而更为科学全面的对移民安置区进行选址。3 基于粗糙数的BWM_ELECTRE方法
3.1 粗糙数BWM方法
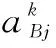
AW=(a1W,a2W,…,anW)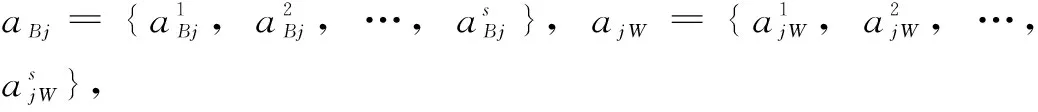
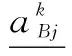
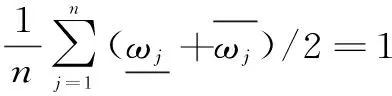
3.2 粗糙数ELECTRE方法
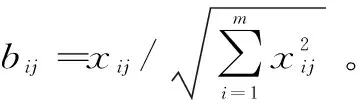
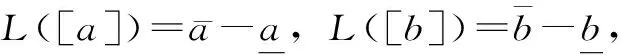
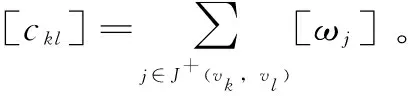
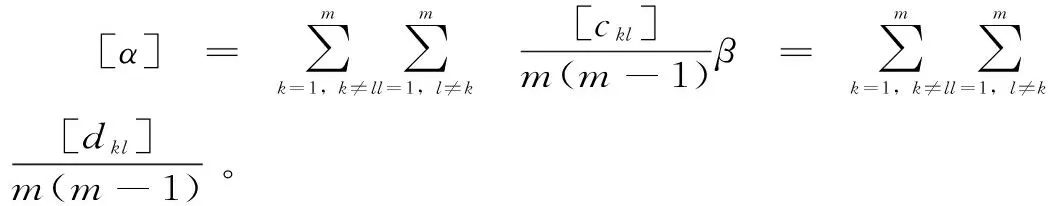
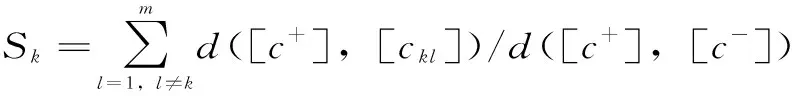
4 实例分析
4.1 粗糙数BWM法确定指标权重

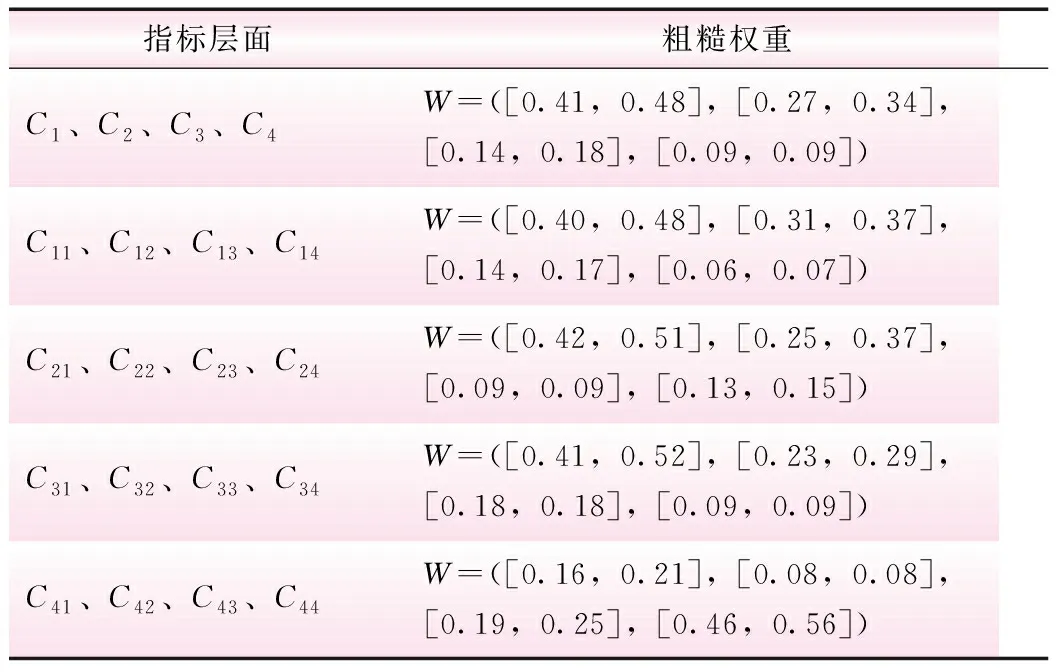
4.2 粗糙数ELECTRE法进行方案排序
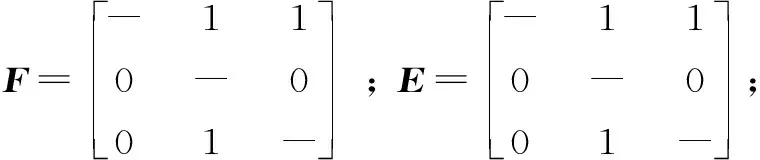
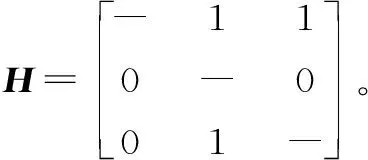
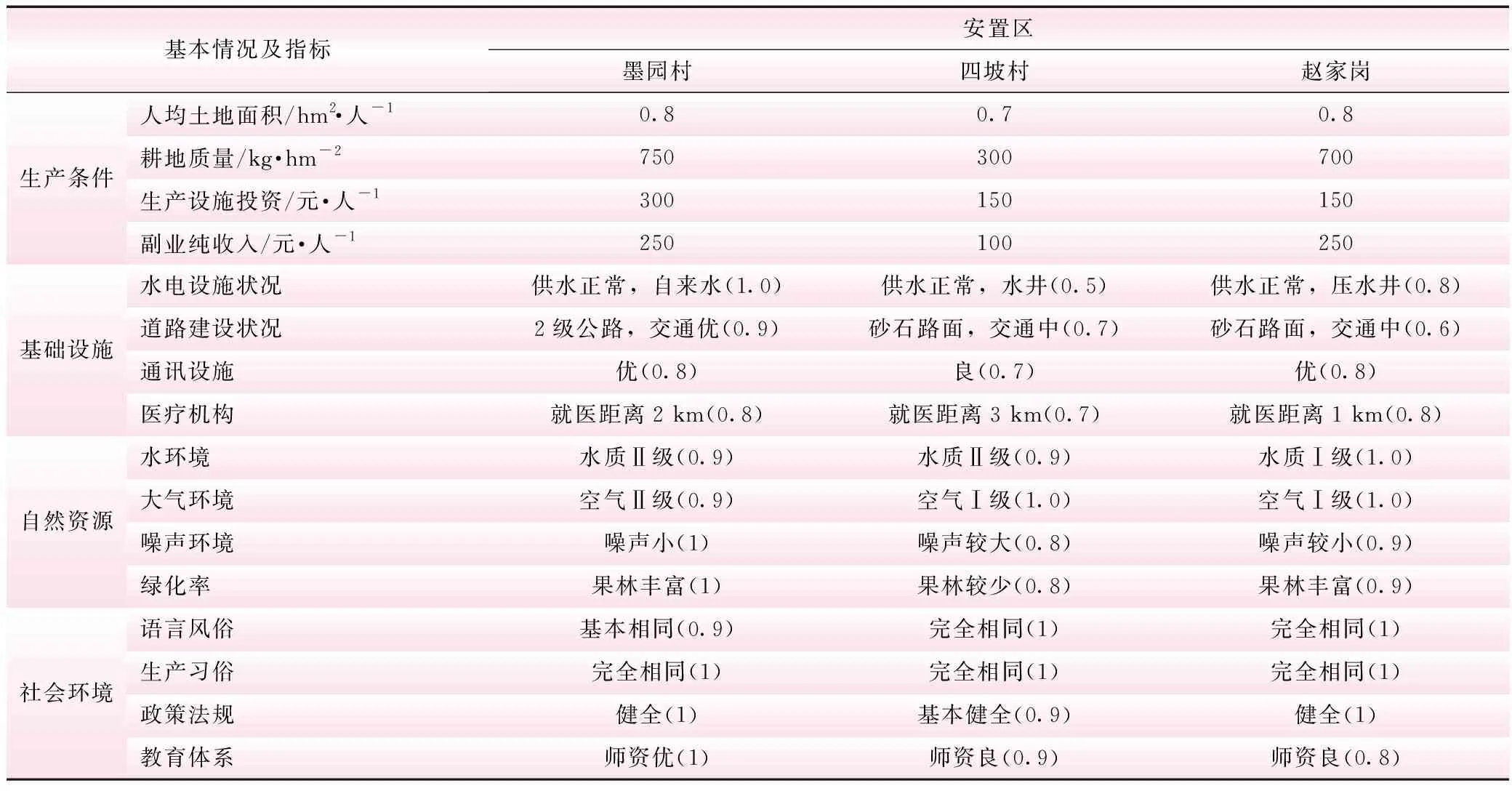
5 结 语
