四轮独立驱动电动汽车ABS与能量回收
2020-07-15李涛涛孙赫阳张袅娜
李涛涛, 孙赫阳, 张袅娜
(长春工业大学 电气与电子工程学院, 吉林 长春 130012)
0 引 言
电动汽车具有节能、环保等优点,在可持续发展战略下成为当今汽车行业研究的热门。目前电动汽车普遍采用ESP(Electronic Stability Program)控制系统,此控制系统利用ABS和ASR(Acceleration Slip Regulation)来控制轮胎滑移率,电动汽车采用轮胎与电机结合,提高了传动效率以及制动过程中制动力矩的快速性,同时制动过程中能量可回收,增加行驶里程。因此,如何在保证车轮滑移率满足安全稳定性的前提下,最大限度地提高能量回收率是一个研究热门[1-2]。
常用的ABS与能量回收控制方法有集成控制和分布式控制。集成控制采用CAN总线技术将各个系统通过CAN集成控制,提高了电动汽车行驶的稳定性、安全性和舒适性[3]。由于抗干扰性差的电机受到干扰后,可能引发系统的失控,分布式控制通过控制滑模算法保证系统的稳定性和电机力矩分配策略保证能量回收[4-8]。文献[6]提出了一种防饱和条件积分滑模算法控制滑移率,为了提高鲁棒性和精确性,采用期望转矩估计附着系数的不确定性上界,从而抑制了滑模系统的抖动。在电机力矩分配策略研究中,文献[8]提出了适用于电动轮汽车再生制动策略,依据车身减速度和Ⅰ曲线来分配前后轮的再生制动力分配,然后采用PID算法修正操作执行机构的力矩。
上述文献通过对单个轮胎分析提出滑移率控制策略,然后进行制动力分配策略,没有考虑轮胎间的耦合。文中针对各个轮胎之间的耦合,通过图论设计了基于多智能体框架下ABS与能量回收联合控制策略,实现了对轮胎间的解耦,在对轮胎保证制动稳定性的前提下,以能量回收最大化为目标,通过液压补偿制动力分配策略对机电复合制动力矩进行分配。
1 车轮模型
系统以保证车轮滑移率最优为目标,四轮独立驱动电动汽车车轮的制动受力图如图1所示。
动力学方程表达式为:

(1)
(2)
Fμ=Fzμ,
(3)
(4)
式中:Fz----轮胎支持力;
Fμ----轮胎对地面附着力;
v----车辆行驶速度;
μ----车轮与地面附着系数;
Tb----车轮的需求制动转矩;
I----转动惯量;
ω----角速度;
R----半径;
λ----滑移率;
d----滑移率受到的随机性干扰。
2 整车转矩分配的控制器设计
电动汽车在直线行驶时,常规工况下制动力矩以转速跟随为目标,在紧急制动情况下,制动力矩以稳定性为目标,当路面附着系数达到极限值时,电动汽车自启动ABS和ASR联合控制。针对电动汽车的ABS和ASR联合控制的工况开展了基于多智能体框架下的滑模控制策略和液压补偿制动力分配策略。控制策略采用分层设计,如图2所示。
上层采用多智能体理论结合滑模控制理论得到电动汽车在联合控制过程中的需求转矩,保证行驶过程的稳定性。下层结合电池状态与电机转矩限制得到实际电机和液压制动力的分配,实现能量回收。

图2 系统结构框图
2.1 基于多智能体的制动力矩控制层
文中图论利用几何学知识,建立描述多智能体之间关系的图G=(V,E,A)。其中V={v1,v2,…,vN}分别代表图G的N个智能体。各个智能体之间的信息交互设为E⊆V×V,并且有eij=(vi,vj)∈E表示智能体i和j之间的信息交互,A=[aij]∈RN×N代表多智能体的邻接矩阵:若有eij∈E,则有aij=1代表有信息交互;否则aij=0。其中aii=0,∀i=1,2,3,4。从智能体i开始与G图中所有其他智能体j信息交互的路径称为智能体i在G图中的树[9]。
在联合控制的情况下,其中四个轮胎的滑移率跟随误差分别作为四个智能体,以滑移率误差跟随等于零作为虚拟领导者。其拓扑结构如图3所示。
由图3可知,文中采用固定的拓扑结构,关联矩阵A、拉普拉斯矩阵L[10]:

(5)
(6)
在多智能体系统中,四个智能体与虚拟领导者之间的权值矩阵B
B=diag(1,1,1,1)。
(7)
为简化计算,设定四个轮胎相同,并在理想状态下对轮胎i进行分析。对式(4)求一阶导数
(8)
对式(4)求二阶导数
(9)
令
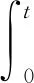
(10)
将式(7)代入式(5)、式(6),得到ABS的一阶状态方程
(11)
式中:
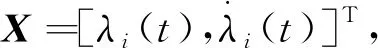
(12)
(13)
(14)
式中:vi0----轮胎i的初始速度。
针对系统的不确定性,选取滑模面为
si(t)=εie1i(t)+e2i(t),
(15)
其中:
e1i=λid-λi,
式中:λid----轮胎i的期望滑移率;
εi----一个正常数。
对式(12)求导得

εie2i(t)+
(16)
式中:

设计控制率
(17)
式中:Z=kisgn(si(t))。
轮胎i与轮胎j之间的滑移率偏差以及滑移率变化率偏差之间的信息交互为
e1ij(t)=λi(t)-λdi(t)-λj(t)-λdj(t),
(18)
j∈Ni,
在直线行驶时, 四个轮胎路面工况相同, 则有
(19)
在多智能体中轮胎i在考虑自身滑移率偏差同时考虑相邻的轮胎j的滑移率以及滑移率变化率的偏差为
(20)
将更新后的滑移率偏差以及滑移率变化率偏差代入式(17),得到基于多智能体的滑移率控制律[9]

(21)
i=1,2,3,4,
下面证明系统的稳定性,四个轮胎跟随虚拟领导者运动为
(22)
将式(19)和式(18)代入式(8)中,得到轮胎i的期状态方程为
(23)
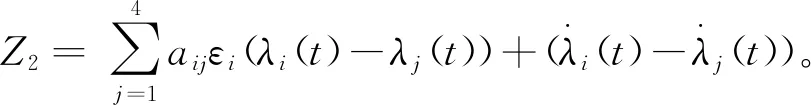
(24)
式中:
ε=diag[ε1,ε2,ε3,ε4],
K=diag[k1,k2,k3,k4],
选择李亚普洛夫函数
(25)
对式(25)求导得




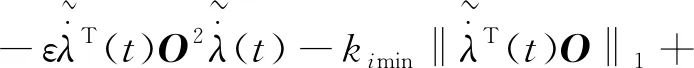
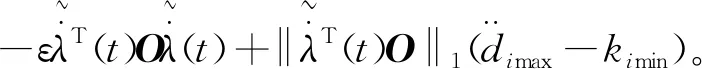
(26)
2.2 基于液压补偿制动的力矩分配层
电动汽车在ABS过程中各个轮胎转矩的制动力需求前面已经分析求得,各个车轮制动力矩需要电机和液压制动协同复合制动。由于电机制动的快速性,且制动过程中伴有能量回收,因此在制动过程中最大化地使用电机制动,采用液压制动补偿的分配策略[11],以达到制动能量回收最大化。由于液压制动与电机制动在制动过程中存在着差异[12],电机制动力矩受到电池soc值、电机转速、最大转矩等诸多因素的影响。文中采用经验公式求得实时状态下电机i最大再生制动转矩[13]。
(27)
式中:Tm,max----电机最大分配的转矩;
Isoc----电荷状态,soc∈(0,1);
p(t)----sigmoid函数保证在低速时断开电机制动;
Tm,n----电机最大制动转矩;
ωi,ωn----分别为当前转速和转速基速。
其中
(28)
式中:kv----倾斜系数;
v----当前车速;
v0----电机制动最低车速。
根据电机i固有特性可得到电机i的制动转矩约束条件
Tmi,min≤Ti≤Ti,max,
i=1,2,3,4。
(29)
通过实时电机i最大再生制动力矩和电机i自身固有的转矩约束条件,计算电机i最大制动力矩为
(30)
电动汽车在ABS过程中,由于制动力矩需求过大,从而导致电机制动力矩无法满足需求转矩,这就需要液压制动力矩补偿所缺少的制动力矩。液压制动补偿力矩的计算
(31)
式中:Tmi----电机i产生的制动力矩;
Thi----液压制动对轮胎i补偿的制动力矩。
通过上式分别得到了轮胎i在再生制动力矩分配中的电机制动力矩以及液压制动力矩。
3 仿真结果
3.1 紧急制动模式仿真
本次仿真实验基于Carsim与Simulink联合仿真,路面工况设置为干水泥路面的仿真条件。电动汽车在ABS过程中四个轮胎理想化滑移率均取λid=0.2,其对应的路面附着系数为0.88。紧急制动情况下,四个轮胎滑移率仿真分别如图4~图7所示。
图4 无ABS制动滑移率
图5 纯液压ABS制动滑移率
由仿真图分析可知,在随机性干扰下,无ABS系统滑移率出现较大抖动后失去稳定,纯液压制动ABS系统滑移率在经过一段时间后达到稳定,但由于液压系统存在迟滞,所以出现较大的抖动,文中提出的控制方法通过电机的快速性与多智能体间的解耦控制,使轮胎在到达理想滑移率的同时能够消除抖动。在制动距离方面,液压ABS制动比无ABS制动缩短了25%~28%,文中的ABS与ASR联合控制策略相较于无ABS制动缩短了31.2%~35.6%。
3.2 连续制动模式仿真
电动汽车在全程路长1 km的干水泥路面上连续进入ABS过程,行驶时间为60 s,在前面已经求得各个轮胎制动力矩的情况下,分别采用并联再生制动和基于ASR+ABS的液压补偿制动的制动力矩分配方法,其仿真图如图8所示。
由仿真图形可知,在制动过程中,基于ASR+ABS的液压补偿制动力矩分配策略由于充分利用了电机的能量回收能力,其比传统并联再生制动力矩分配的能量回收率提高了24%。
4 结 语
提出了基于多智能体框架下的ABS与ASR联合仿真策略,并进行Carsim和Simulink联合仿真,其结果验证了该策略的可行性。仿真结果表明,基于多智能体框架下的ABS与ASR联合仿真在紧急刹车时实现滑移率跟随并且消除抖动,同时缩短制动距离满足制动安全性的要求,连续ABS过程在满足制动安全性的前提下,基于ABS与ASR的液压制动力矩补偿分配控制相比较于并联再生制动控制,提高了能量回收率。
1)将多智能体理论运用到ASR控制中,实现了滑移率误差的跟随,保证在紧急刹车时的滑移率稳定性,增加了电动汽车行驶的安全性。
2)在电动汽车ABS再生制动过程中采用液压制动补偿策略,极大地发挥了电机制动的快速性与能量回收性,提高了电动汽车的续航能力。
