理清结构,强化方法
2020-07-14王平
王平
摘要:苏科版初中数学七年级上册第4章第3节《用一元一次方程解决问题》没有揭示实际问题中数量关系的结构,给出的分析问题的方法(策略)也比较“杂”。这就导致教学主线不清晰,学生学习(尤其是迁移运用)难度较大。研究教材中有关题目的特点后,发现:教学时,可以数量关系的结构变化为主线,调整题目顺序;以列表格、画线形图等核心方法为主线,聚焦数学建模;并基于教学主线,进行例题分析的呈现、例题拓展的思考、例题配套的练习等方面的附加设计。
关键词:《用一元一次方程解决问题》数量关系表格线形图
在现行初中数学课程中,“用方程解决问题”是培养学生数学建模素养的重要模块。其中,“用一元一次方程解决问题”的有关内容是基础。对此,苏科版初中数学七年级上册第4章《一元一次方程》安排了72道用一元一次方程表示实际问题中数量关系的题目,该章第3节《用一元一次方程解决问题》将例题按照“表格”“线形图”“扇形图”“柱状图”等分析问题的方法(策略)组织呈现。但是,教材没有进一步揭示实际问题中数量关系的结构,给出的分析问题的方法(策略)也比较“杂”(有些方法在后续的“用二元一次方程组解决问题”“用分式方程解决问题”“用一元二次方程解决问题”中再也没有提到过)。这就导致教学主线不清晰,学生学习(尤其是迁移运用)难度较大。
针对这一情况,笔者带领一些教师研究教材中有关题目的特点,并重点研究实际问题中数量关系的结构和分析问题的核心方法,从而重组设计了“用一元一次方程解决问题”的有关内容。
一、以数量关系的结构变化为主线,调整题目顺序
分析教材中有关的实际问题中数量关系的个数后,我们发现:蕴含2个数量关系的题目有9道,占12.5%;蕴含3个数量关系的题目有22道,占30.6%;蕴含4个数量关系的题目有33道,占45.8%;蕴含5个及以上数量关系的题目有8道,占11.1%。
进一步分析教材中有关的实际问题中数量关系的结构后,我们又发现:很多题目中的数量关系都包括“a+b=c”“ab=c”这两个最基本的结构,根据题意列出的方程都可以看作这两个最基本结构的复合结构。具体来说,以下三种结构出现得最多:
蕴含2个数量关系的题目列出的方程都是“ab+c=d”的结构,即将“a+b=c”中的“a”用“ab=c”替换。例如:“把50 kg大米分装在3个同样大小的袋子里,装满后还剩余5 kg,求每个袋子可装大米的质量。”本题蕴含了2个数量关系:一是“袋子个数×每袋质量=袋子装的总质量”,即“ab=c”的结构;二是“袋子装的总质量+剩余质量=总质量”,即“a+b=c”的结构。如果设每个袋子可装大米的重量为x kg,那么,根据题意可得3x+5=50,即“ab+c=d”的结构。
蕴含3个数量关系的题目中有13道(占59.1%)列出的方程都是“ab+cd=e”的结构,即将“ab+c=d”中的“c”用“ab=c”替换。例如:“小亮买5本练习本和2支圆珠笔一共用了5.5元,圆珠笔每支1.5元,求练习本的单价。”本题蕴含了3个数量关系:一是“练习本数量×练习本单价=练习本的费用”,即“ab=c”的结构;二是“圆珠笔数量×圆珠笔单价=圆珠笔的费用”,即“ab=c”的结构;三是“练习本的费用+圆珠笔的费用=总费用”,即“a+b=c”的结构。如果设练习本的单价为x元,那么,根据题意可得5x+1.5×2=5.5,即“ab+cd=e”的结构。
蕴含4个数量关系的题目中有16道(占48.5%)列出的方程都是“ab+c(d+e)=f”的结构,即将“ab+cd=e”中的“d”用“a+b=c”替换。例如:“篮球队参加篮球联赛,某队赛了12场,共得20分。已知胜一场得2分,负一场得1分,那么该队负了多少场?”本题蕴含了4个数量关系:一是“胜的场数+负的场数=总场数”,即“a+b=c”的结构;二是“胜的场数×胜场单场得分=胜场得分”,即“ab=c”的结构;三是“负的场数×负场单场得分=负场得分”,即“ab=c”的结构;四是“胜场得分+负场得分=总得分”,即“a+b=c”的结构。如果设该队负了x场,那么,根据题意可得1·x+2(12-x)=20,即“ab+c(d+e)=f”的结构。
根据上述分析,我们应该遵循学生的认知特点,基于题目中数量关系的个数从少到多、结构从简单到复杂的原则,调整教材题目的顺序,并适当增、减题目,保持各种“结构”数量的相对均衡。在不改变课时数的情况下,可以这样设置例题:第1课时设置两道蕴含2个数量关系的题目和一道蕴含3个数量关系的题目;第2课时设置三道蕴含4个数量关系的题目;第3—6课时则各设置若干蕴含4个及以上数量关系的题目(这几个课时重点考虑分析数量关系的方法,后文还有叙述)。
这样的设置确保学生能在第1课时中基本理解题目中数量关系的结构,特别是充分认识“a+b=c”“ab=c”这两个最基本的结构;在第2课时中牢牢掌握教材中出现次数最多的“ab+c(d+e)=f”结构;在后续的课时中学会分析各种其他类型的数量关系结构,初步感受数学建模的方法。
二、以列表格、画线形图等核心方法为主线,聚焦数学建模
翻阅苏教版小学数学教材,可以发现,学生在小学三年级时,就开始尝试用列表格和画线形图的方法分析实际问题。纵观苏科版初中数学教材中“用方程解决问题”的有关内容,可以發现:分析实际问题的核心方法是列表格;在一些有关行程、工程等的问题中,再辅以画线形图。
因此,对于“用一元一次方程解决问题”的有关内容,略去教材中的“扇形图”“柱状图”等分析问题的方法,强化列表格、画线形图这两种核心方法,更有利于培养学生分析问题的能力,提升学生数学建模的能力。
于是,在第1课时第1道例题的分析上,我们首先关注了表格的“诞生”:
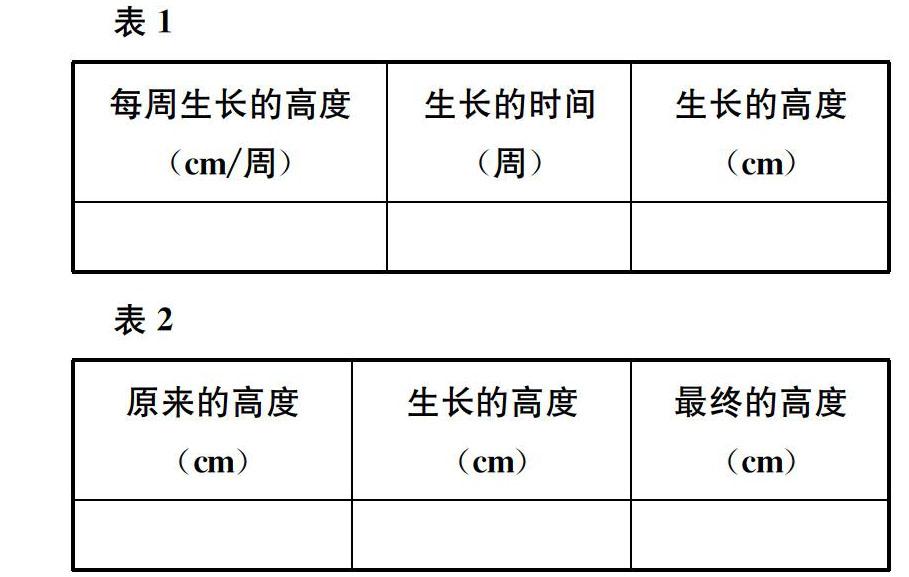
例1小颖种了一株树苗,刚种下时,树苗高为40 cm,以后每周可长高15 cm。按照这样的生长速度,多少时间后树苗可长到1 m?
分析本题蕴含了两个数量关系:(1)树苗每周生长的高度×生长的时间=树苗生长的高度;(2)树苗原来的高度+树苗生长的高度=树苗最终的高度。
这两个数量关系都可以列出相应的表格(见表1、表2)。
(cm)这是一道蕴含2个数量关系的简单题目。在这道题目的分析过程中,既关注数量关系是什么,又关注怎么列表格——其实质是每一个表格对应一个数量关系,表格的“诞生”和数量关系的分析紧密相连。
从这道例题开始,第1—5课时每道例题的分析都围绕“寻找数量关系—建立表格—列方程解决问题”的流程展开。当然,在这一流程中,我们还关注表格的简化——后续的例题主要借助一个表格分析问题。
第4—5課时每道例题的分析在借助表格的基础上,还辅以画线形图;第6课时每道例题的分析则不再借助表格,只是利用线形图。这样的设计,一是体现表格的“基础”作用,即表示线形图中的线段时,还可以借助表格把数量关系用字母表示出来;二是重视线形图的作用,教会学生怎么画出线形图、怎么在线形图上标注、怎么利用线形图寻找数量关系;三是让学生体会到表格只是一个工具,在分析问题的能力到达一定的程度后,是可以通过思维“隐化”的。
三、基于教学主线,进行附加设计
在重组设计“用一元一次方程解决问题”的有关内容时,我们还进行了例题分析的呈现、例题拓展的思考、例题配套的练习等方面的附加设计,力图促使学生的学习更主动、更深入。
(一)关于例题分析的呈现
对于每个课时的例题,有的完整呈现分析过程和解答过程(一般是每个课时的第1道例题),有的只给出分析框架,有的只给出分析中表格的栏目,还有的只给出题目。多样的呈现形式一方面为学生掌握列表格、画线形图分析问题的方法提供循序渐进的步骤,另一方面也让学生能方便地使用,从而使“教材”变成“学材”;同时,也符合样例的不完整、渐减提示、步骤编码等设计理论。
(二)关于例题拓展的思考
对于每个课时,我们还设计了一些思考问题,比如“尝试归纳这节课例题中数量关系的特征”“谈一谈如何借助表格解决本类问题”“说一说借助线形图解决问题的步骤”等,从而拓展例题的空间,促使学生深入理解每个课时实际问题的结构,或体会每个课时解决问题的方法,或从不同的角度认识问题等。
(三)关于例题配套的练习
对于每个课时,我们还从多个版本的教材中选出了符合教学目标(与例题相配套)的题目,作为课上和课后的练习题。同时,兼顾呈现形式和难易顺序设计:课上、课后练习的第1题都呈现分析框架,使之直指相应课时的核心内容和方法,帮助学生巩固课堂所学;从第2题开始,只给出具体的题目,不限制学生的思维;从第1题到最后1题,基本按照从易到难的顺序编排;最后1题一般打上“*”,供学有余力的学生思考。
