武汉市2019-nCoV新型冠状肺炎预测模型分析

侯文涛，李 磊

(运城学院 数学与信息技术学院，山西 运城 044000)

引言

2019新型冠状肺炎，即2019-nCoV，是目前新发现的又一种可以在人与人之间传染的冠状病毒，首次发现于2019年武汉病毒性肺炎病例中。新型冠状病毒主要的传播方式是呼吸道飞沫传播和接触。2019年12月，湖北省武汉市在展开的流感及相干疾病监测中，发现多起病例感染病毒性肺炎，现被证实为新型冠状病毒感染，之后新冠肺炎感染者数量开始在武汉市内急剧上升，后确定该病毒具有人传人风险，随之中国其他地区也出现感染者，同时全世界大多数国家都出现了感染病例，引发全球的重视。目前，新型冠状肺炎是世界众多学者关注和研究的重点问题之一。颜铭江利用改进的SEIR模型预测疫情的进一步发展，计算每日有效再生数的变化，预测在2020年4月19日所有的患者将全部出院，累计确诊患者为66487[2]；蔡洁构造SEIR模型模拟武汉市新冠肺炎的发展趋向，得出疫情的“拐点”将会出现在采取封城方法后的第35天，同时预测疫情在4月底将会根本得到控制[3]；朱仁杰以SIR模型为基础，对7个国家疫情的发展情况进行预测，并剖析各国减少接触率等防治措施对疫情发展的影响，揭示了各国的防疫现状以及减少接触率的措施的重要；王思远采用SEIR模型预测2019-nCOV疫情数据，有效的预估了疫情发展趋势，并根据新的数据不断自动更新未来疫情发展[5]；林挺葵结合Holt两参数指数平滑模型预测疫情的未来发展趋势，结果表明在现有高效防控措施下，粤西地区及各地级市新冠肺炎疫情正在停止恶化，有望在2月底出现“拐点”[6]。本文在参考已有文献的基础上，结合所学统计预测方法[7]，对收集的武汉新型冠状疫情的日增长数据构建Holt双参数指数平滑模型与求和自回归移动平均ARIMA模型，并选择较优模型预测武汉2月11日至13日新型冠状疫情的新增感染人数，对武汉新冠肺炎疫情的预防控制提供理论支持，为新冠疫情的研究提供新的参考。

1. 理论方法

1.1 Holt两参数模型

指数平滑法的基本思想就是预测值是以前观测值的加权和，并且对不同的数据赋予不同的权数，越接近预测期的数据给予越大的权数，越远离预测期的数据赋予越小的权数；基本公式为

St=a*xt+(1-a)st-1

式中St为时间t的平滑值；xt为时间t的观测值；St-1为时间t-1的平滑值；α为平滑参数，其取值范围为[0，1]。Holt双参数线性指数平滑法[8]是将趋势序列直接进行平滑，对原序列进行预测的，因此平滑公式为

St=axt+(1-α)(St-1+rt-1，

rt=β(St-St-1)+(1-β)rt-1，

式中{St}为修匀后的预测序列；xt为时间t的观测值；α，β为平滑参数，其取值范围为[0，1]。{rt}为趋势序列，需要注意的是趋势序列{rt}也是一个随机序列。预测公式为

Pt+l=St+l*rt

式中Pt+l为时间t向前l期的预测值；l为向前预测的期数[10]。

1.2 ARIMA模型

ARIMA模型[9]，中文名称为求和自回归移动平均模型。是由美国统计学家博克思(Box)和詹金斯(Jenkins)在20世纪70年代初提出的一种时间序列的预测方法。ARIMA(p，d，q)模型具有如下结构

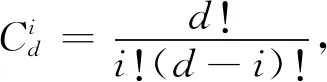
式中{εt}为零均值白噪声序列。ARIMA建模流程图如图1所示。

1.3 模型评价

在利用模型拟合数据时不可避免地会存在误差，那么模型对实际值拟合的程度便称为拟合优度，拟合优度的统计量称为可决系数或者确定系数(R2)，计算公式为

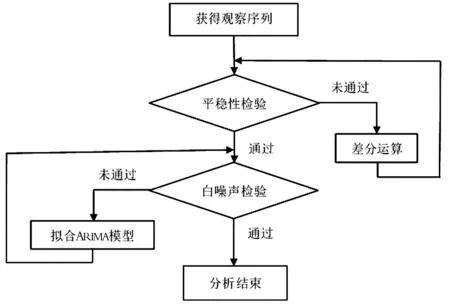
图1 ARIMA建模流程图

2. 实证分析

本文所使用的数据来源于2020年1月16日至2月16日中国卫生健康委官方网站(http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml)[11]和中国湖北省卫生健康委官方网站(http://wjw.hubei.gov.cn)[12]所公布的数据。

使用R软件绘制2020年1月16日至2月10日武汉地区新型冠状病毒的日增长人数时序图，该序列呈现出明显的上升趋势，随着时间天数的增加，日增感染人数保持正值，感染人数持续上升，详见图2。

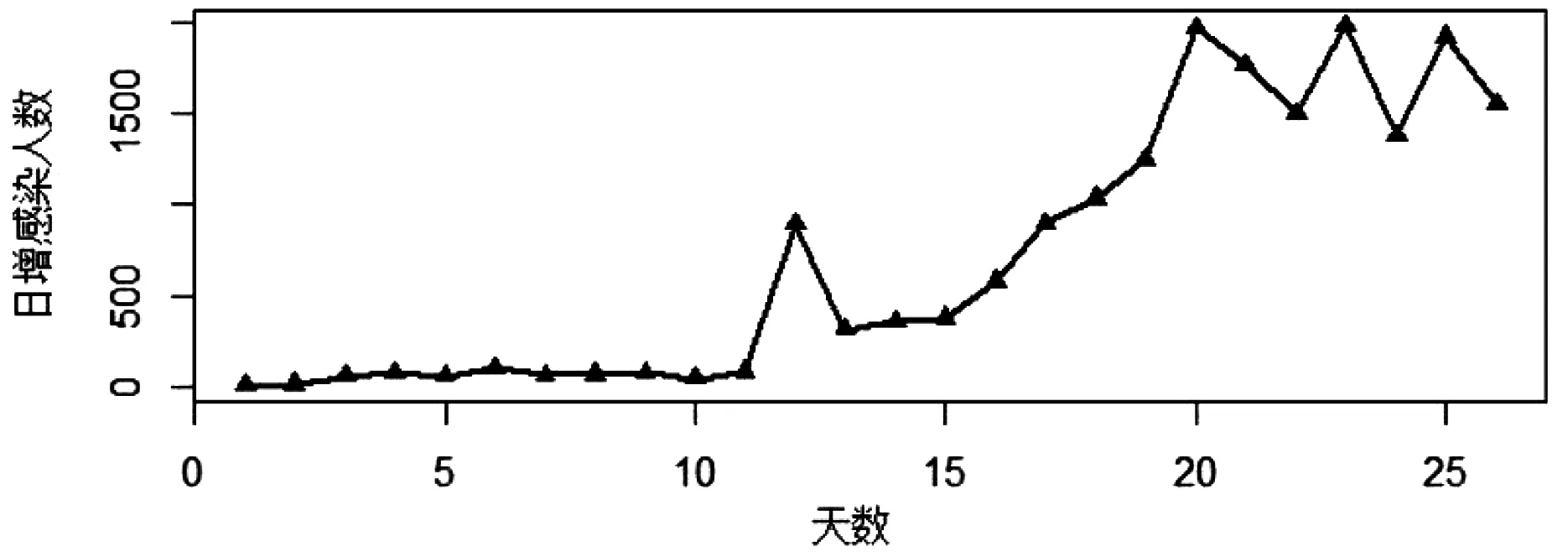
图2 武汉新冠肺炎每日新增感染人数时序图

2.1 Holt模型在武汉市新冠肺炎的应用

借助R语言3.6.2，将数据进行简单处理之后读入序列，建立Holt双参数平滑模型，经过反复实验得到Holt双参数平滑系数α=0.57，β=0.06，详见表1。说明修匀后的预测序列{St}在未来预测中，近期数据对预测数据的影响比较大；趋势序列{rt}在未来预测中，近期数据对预测数据的影响比较小；此时模型的误差平方和达到最小，拟合的指数平滑模型为

通过采取以上一系列技术和管理措施，解决了盾构穿越高铁桥梁桩基施工难题，确保了高铁桥梁和车辆运行安全和隧道工程实体质量。本工程的施工经验，也应用到了盾构下穿铁路站场路基施工中，对将来其他类似工程施工具有一定的参考借鉴作用。

St=0.57xt+0.43(St-1+rt-1)

rt=0.06(St-St-1)+0.94rt-1

预测模型为

Pt+l=1696.91+l*59.47

表1 Holt双参数模型系数表

通过预测模型Pt+1=1696.91+l*59.47，计算1月16日至2月10日的估计值，并考虑该模型预测结果的滞后性，结果如表2。将真实值与估计值绘制在一张图中，如图3，图中黑色实线表示真实值，红色虚线表示估计值，可以看出两条曲线在前期几乎重合，动态趋势也基本吻合，Holt双参数线性指数平滑模型对新增感染人数拟合效果很好。

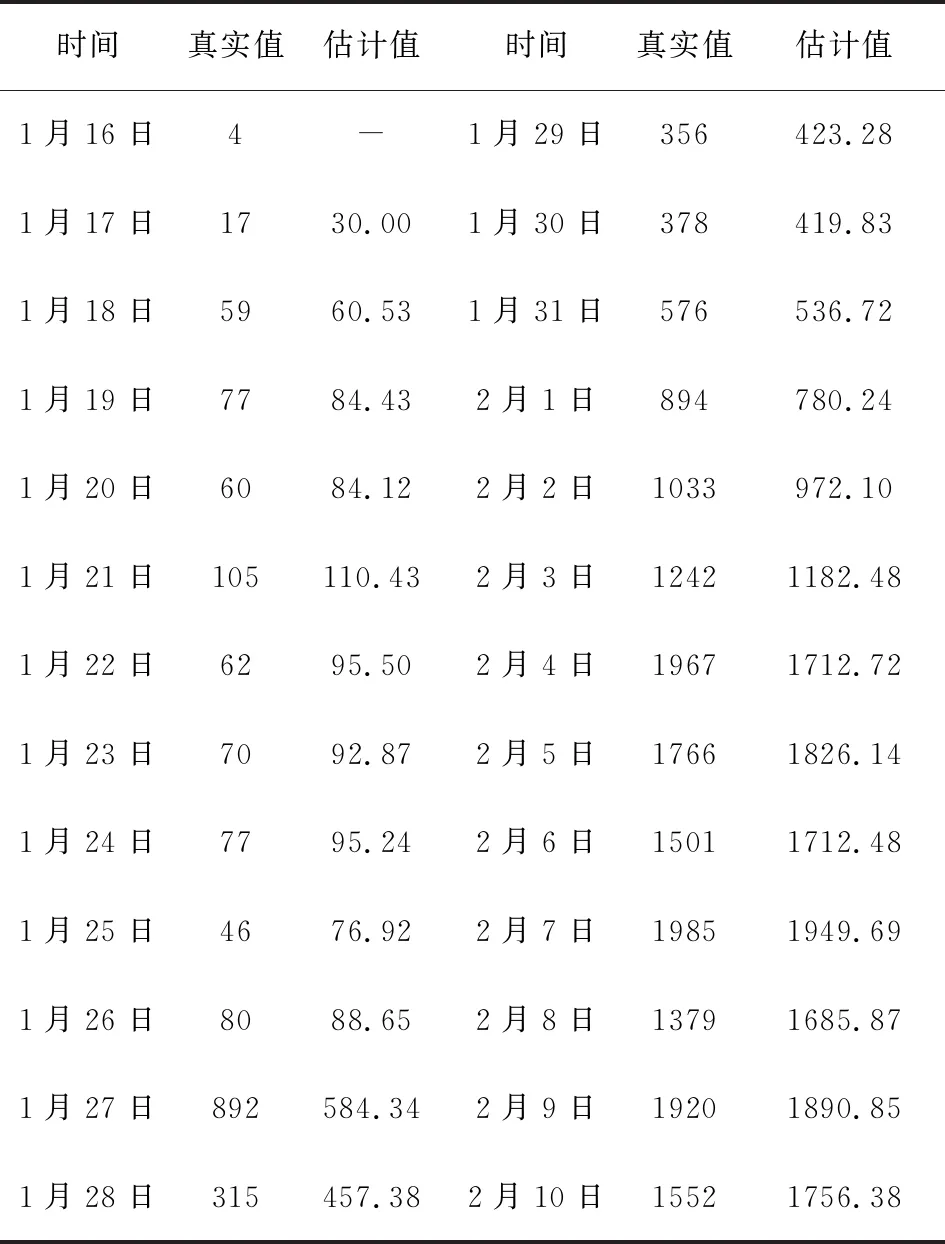
表2 Holt双参数线性指数平滑法计算结果表

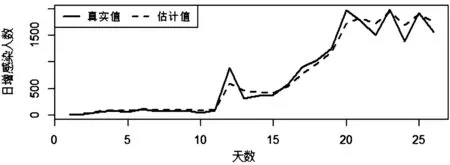
图3 Holt双参数线性指数平滑模型拟合图

2.2 ARIMA模型在武汉新型肺炎的应用

2.2.1 序列平稳化

由图2可知，序列呈现曲线上升趋势，是非平稳序列。对序列进行二阶差分，差分后的序列进行单位根检验，其中P=0.02182，小于显著性水平0.05，序列趋于平稳。详见表3。

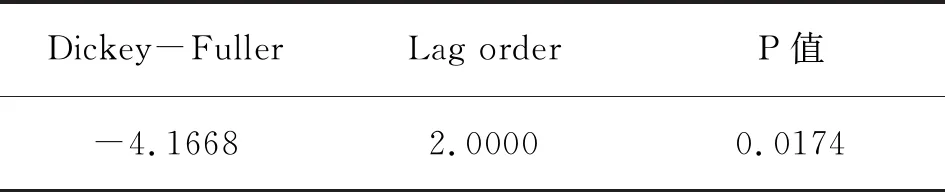
表3 平稳性检验表

alternative hypothesis:stationary

将差分后的序列延迟6期、延迟12期、延迟18期分别进行白噪声检验，，结果如表4，其中P值均小于显著性水平0.05，序列是非白噪声序列。

表4 ARIMA模型白噪声检验表

建立ARIMA(p,2,q)模型，使用R软件，将p、q的可能取值0、1、2进行由低阶向高阶进行测试，并依据AIC最小准则，经过反复实验，得出当p=1,q=1时，AIC值最小，所以ARIMA(1,2,1)模型为最优模型，故序列采用ARIMA(1,2,1)模型进行拟合，详见表5。

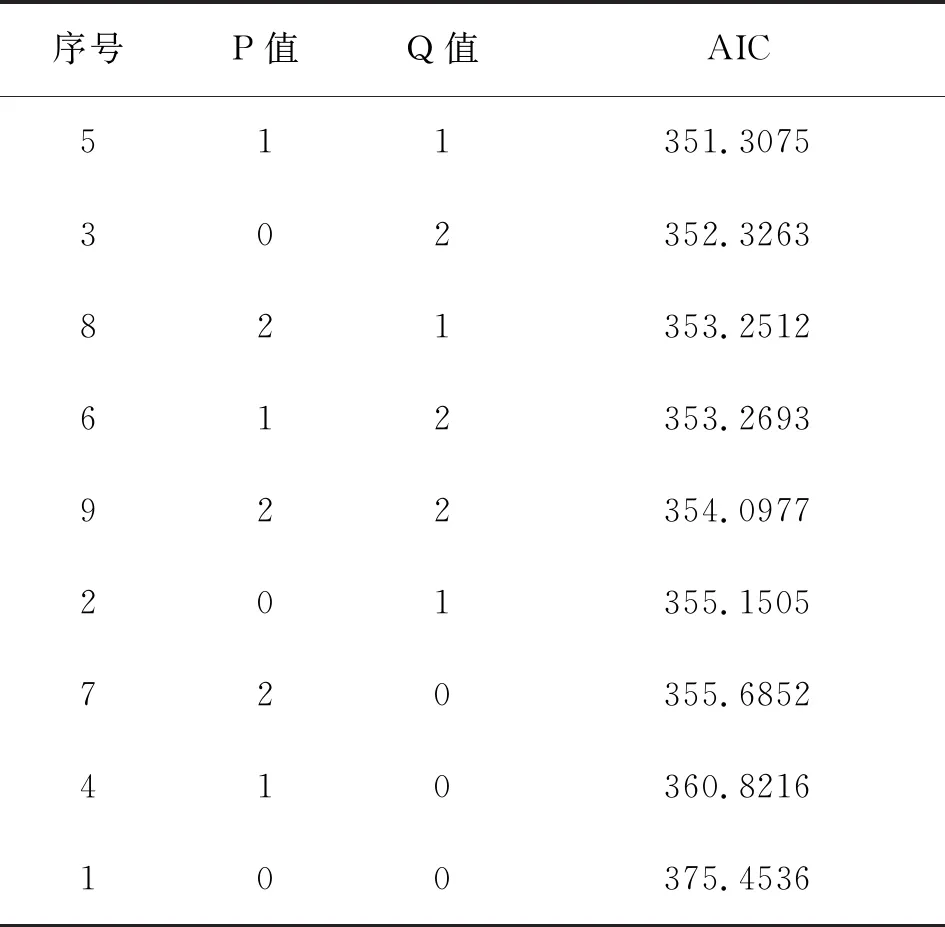
表5 ARIMA模型AIC值计算表

2.2.3 参数估计与模型检验

利用ARIMA(1,2,1)模型对序列进行拟合，并估计模型参数，模型的口径为:

Xt=-0.4759Xt-1+qt-qt-1;εt～N(0,87009

对模型的系数进行检验，P值均小于显著性水平0.05，表明模型ARIMA(1,2,1)中所有的系数都通过了t检验，建立具有统计学意义。详见表6。

表6 ARIMA模型系数表

对ARIMA(1,2,1)模型的残差进行LB检验，结果显示ARIMA(1,2,1)模型的残差序列为白噪声序列，说明模型残差部分是由随机因素造成的，信息已充分提取，满足ARIMA的前提假设。详见表7。

表7 ARIMA(1,2,1)模型白噪声检验表

通过ARIMA(1,2,1)模型计算1月16日至2月10日的估计值，详见表8。如图4，将真实值与估计值绘制在一张图中，图中黑色实线表示实际值，红色虚线表示估计值，可以看出两条曲线在前期几乎重合，动态趋势也基本吻合，ARIMA(1,2,1)模型对新增感染人数拟合效果也很好。

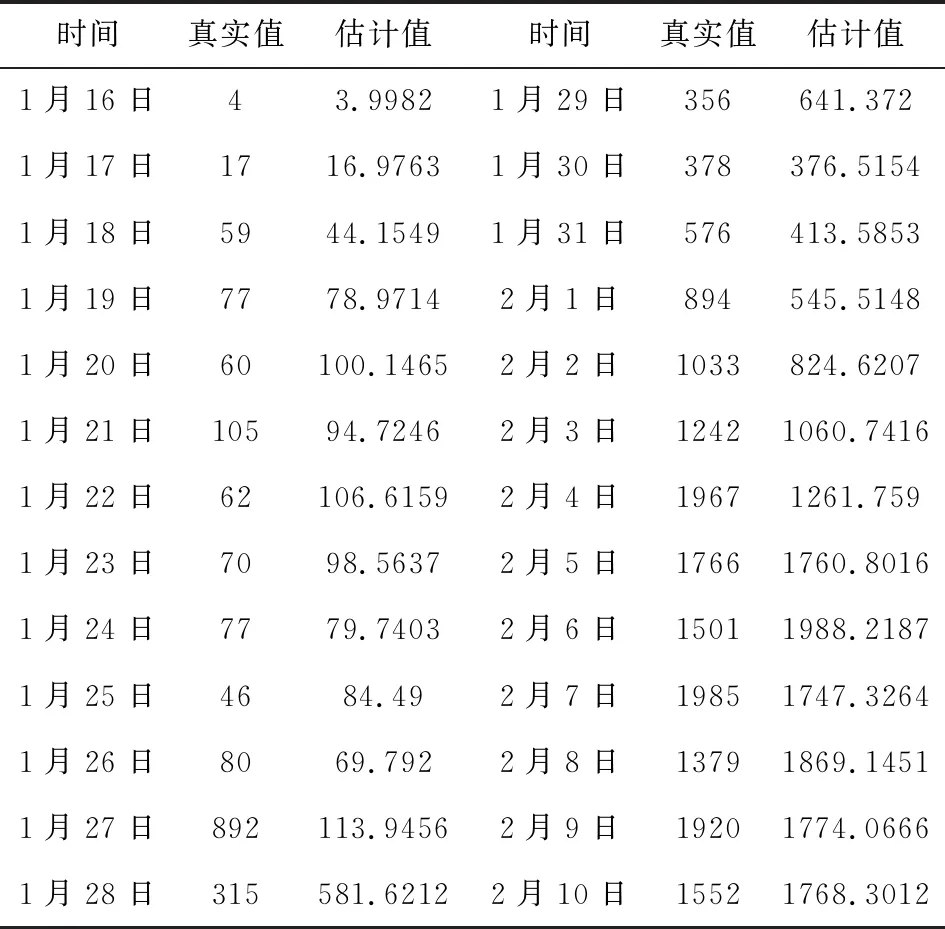
表8 ARIMA模型计算结果表

2.3 预测分析

分别计算两个模型的可决系数R2，Holt双参数指数平滑模型的可决系数为0.968,ARIMA(1,2,1)模型的可决系数为0.834,Holt双参数指数平滑模型的拟合程度更好。

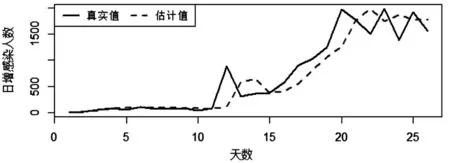
图4 ARIMA模型拟合图

选用拟合度较好的Holt模型对武汉2月11日到2月13日新冠肺炎每日新增感染人数做出预测，并结合实际值进行对比。详见表9，绘制真实值和预测值的折线图，详见图5。因2月12日至2月13日的数据中含有临床值感染人数数据，本文除去了临床值对研究的影响。模型预测值显示，武汉2月11日至13日新型冠状肺炎的日感染人数持续增加。但结合实际日感染人数，实际值普遍低于预测值。由此可知，之前一段时间的疫情防治措施已经初步取得成效，疫情爆发期已经过去，开始进入稳定期[13]。

从实际数据分析，武汉疫情的发病数据整体呈现先上升后下降的趋势，在2月13日达到最大值。1月16日到2月13日之前，日感染人数呈现上升趋势，2月13日之后，日感染人数呈现下降趋势。直到3月18日之后，日感染人数接近于0。利用Holt模型对武汉日感染人数进行预测，并于实际值比较，分析得出武汉疫情的稳定期已经到来，对于整体把握新型冠状疫情的走势具有重要意义。

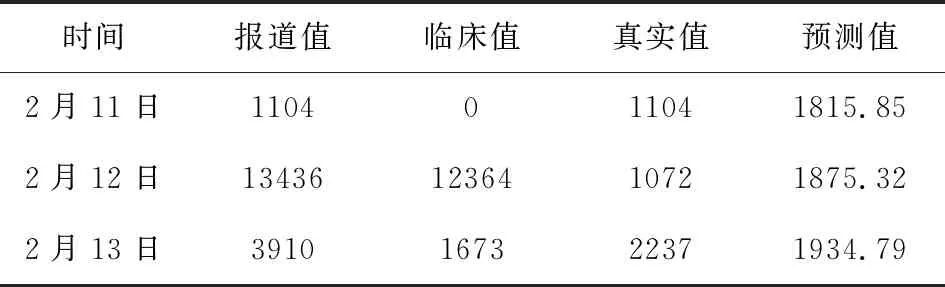
表9 Holt双参数指数平滑模型预测结果表

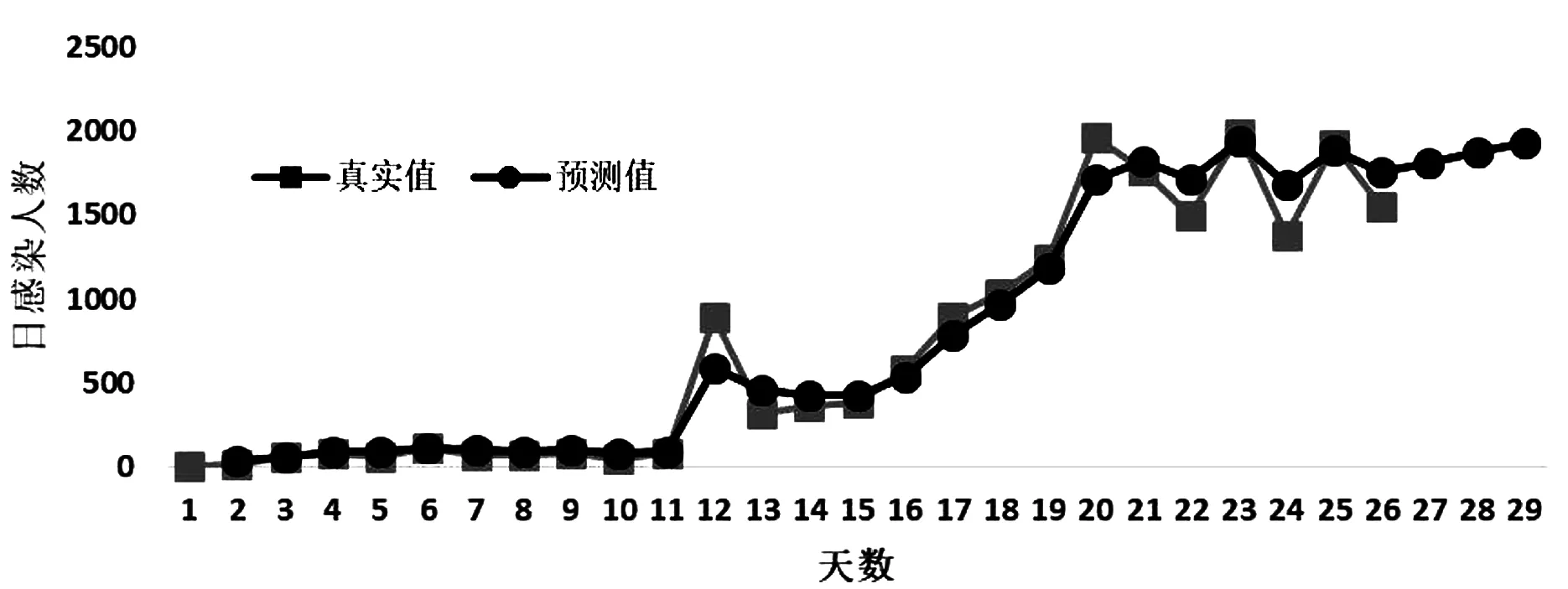
图5 Holt双参数指数平滑模型预测图

3. 小结

新型冠状病毒自今年爆发以来，席卷多个国家，在全球范围内造成了不可估计的损失，是我国乃至世界面临的最严重的流行疾病问题之一。建立有效的统计预测模型预测新冠肺炎的发病情况，对新冠肺炎的预防和研究具有重要意义。本文利用2020年1月16日至2月13日国家卫生健康委员会和湖北省卫生健康委员会发布的新冠肺炎数据，分别建立了Holt双参数线性指数平滑模型和ARIMA(1,2,1)模型。其中，ARIMA模型的拟合系数为0.834，Holt双参数线性指数平滑模型的拟合系数为0.968，Holt双参数线性指数平滑模型的拟合效果较优。最后，使用模型对2月11日至2月13日的新增感染人数做出预测，实际值低于预测值，与武汉疫情发病数据先上升后下降的整体变化趋势相吻合。研究表明在疫情爆发期前一段时间的疫情防治措施已经初步取得成效，人们的防疫意识也明显增强。证明之前的封城和居家隔离措施是正确有效的，接下来仍然需要努力，使得疫情的“拐点”早点到来。