基于保密传输的单通道图像盲复原算法研究
2020-07-14张晓敏王尔馥
张晓敏,王尔馥
(黑龙江大学 电子工程学院,哈尔滨 150080)
0 引 言
盲源分离( Blind Source Separation, BSS)[1-2]算法作为信息处理领域的重要技术之一,在近几十年中得到了迅速发展并获得广泛关注,它可以在信号混叠的情况下,提取出感兴趣信号,进而恢复出无法直接观测的源信号信息,因此,对于在复杂的通信环境中,盲源分离算法对提高通信系统适应的能力有着重要的现实价值与实际意义[3]。同时BSS也成功地应用于雷达数据分析[4]、地球物理学[5]、生物医学[6]、语音及图像处理等领域。
本文旨在保密传输过程中先验信息受限的情况下,通过无法直视的图像观测信号,利用BSS实现混叠图像信号的源分离,进而恢复出原始图像信息。而在现实环境中不会总存在信号的观测数目m等于源信号数目n的理想状态,例如在m 变分模态分解[7,15]是基于求其约束变分模型最优解,进而实现混叠信号的自适应分解,它利用希尔伯特(Hilbert)变换、维纳滤波、混合频率及外差法解调等算法,将一个复杂的混叠信号移入变分模型中,最后分解为一定数量特定稀疏性的模态分量uk的过程(uk也被称为本征模态函数(Intrinsic Mode Function, IMF))。 1)每个uk利用希尔伯特变换求得其解析信号,并进而求其单边频谱,则第k个模态的解析信号表达式为: (1) (2) 3)针对每个模态的宽带通过解调信号的H1,即梯度的L2范数,进行估计,其转化为数学语言为: (3) 4)VMD的主要任务是要分解出的IMF的频带尽可能的紧凑,即聚集到其中心频率,对频带搬移后就是聚集到零频附近,因此上式进一步得到约束最小化问题的数学形式的表达式为: (4) 其中{uk}:={u1,…,uK},{wk}:={w1,…,wK}分别为所有模态函数的分量及中心频率集。 5)重构约束,将拉格朗日乘子λ与二次惩罚因子α引入该约束问题模型,使其带约束的最优化问题的求解转化为不带约束的最优化问题的鞍点。其中α在有限权重系数情况下有良好的收敛性,λ可以实现很好的约束性,因此得到非约束—扩展的拉格朗日函数: (5) 2)n←n+1。 3)k=1∶K,w>0。 (6) (7) (8) 4)满足约束迭代条件,给定任意正数ε>0,直至收敛,输出k个模态分量,否则返回步骤2)~3)。 (9) 图1 盲源分离数学模型Fig.1 Mathematical model of blind source separation 盲源分离的基本数学模型见图1。 对盲源分离问题进行建模,给出线性瞬时混合情形下的盲分离问题的数学表达式为: x(t)=As(t) (10) 式中s(t)=[s1(t),…,sn(t)]为n路源信号的矢量;x(t)=[x1(t),…,xm(t)]为m路观测信号的矢量;A为线性混合矩阵。基于单通道特殊情况下令m=1。若在信号传输过程中加入噪声信号n(t)的情况下,则原系统建模为: x(t)=As(t)+n(t) (11) 式中n(t)=[n1(t),…,nm(t)]T为加性环境噪声矢量。经过分离矩阵W的反变换,实现尽可能多地分离出源信号s(t)(y(t)为源信号的估计)。 y(t)=Wx(t) (12) 该算法是通过VMD将一个混叠图像输入信号分解为一系列离散数量的模态分量uk,最后利用分解获得的IMF通过快速独立分量分析重构出原始图像信号。 具体步骤如下: 1)选取标准测试图片,并选择混沌信号作为遮掩信号,将系统随机生成1×n混合矩阵(n与源信号数量相等)与源信号信息线性混叠成一路观测信号x(t)。 3)将x(t)和其分解模态函数分量uk构成多维观测信号。 4)通过FastICA估计得到原图像信息。 从标准图库中选取两幅图片“Lena”和“Cameraman”的灰度图像作为源信号的图像信息,见图2。此外,由于在混沌系统理论中,Chen混沌拥有更加丰富的动力学行为,因此也使在保密传输过程中图像信息的盲复原得到可靠保证,本文选择Chen混沌作为图像信号盲复原的遮掩信号[16]。 根据VMD原理设定图像混叠信号分解的模态分量个数k,通过不同k值来提取原图像信息,进而达到最大优化的盲图像信息的复原。初始化VMD相关参数,α=2 000,τ=0,ε=1e-7,初始化模态数k=2(k≥2,这里将一路观测信号补为正定模式)。 图2 源信号图像信息Fig.2 Image information of the source signal 将两路原图像信号与一路Chen混沌信号线性混叠为一路混合信号,进而根据混合图像信号信息进行VMD分解,见图3~图5。不同k值VMD-BSS 法得到的各模态中心频率见表1。 表1 不同k值 VMD-BSS 算法得到的各模态中心频率w 由表1及图3~图5可见, 当k=4时,其出现了w相近的IMF,即为过分解现象,故选择k=2、k=3时对图像信息进行盲提取检测。 图3 k=2,VMD分解与对应频谱(左)中心频率w的演变(右)Fig.3 k=2, spectrum corresponding of VMD decomposition (lift) evolution of center frequency(right) 图4 k=3,VMD分解与对应频谱(左)中心频率w的演变(右)Fig.4 k=3, spectrum corresponding of VMD decomposition (lift) evolution of center frequency(right) 图5 k=4,VMD分解与对应频谱(左)中心频率w的演变(右)Fig.5 k=4, spectrum corresponding of VMD decomposition (lift) evolution of center frequency(right) 仿真1:初始化模式个数k=2,k=3,无噪声状态下观测信号图像信息与提取后图像信息见图6和图7。 图6 k=2,无噪情况下观测信号图像信息与提取后图像信息Fig.6 k=2, Image information of observation signal and extracted signal without noise 由提取后图像,通过观测可知,无噪情况下k=2时,图像复原效果较好,故选择k=2时检测加入高斯白噪声后的图像盲提取效果。 仿真2:k=2时,有噪声状态下(噪声强度为-20、-10 dbw),观测信号图像信息与提取后图像信息见图8和图9。 图8 -20 db时,观测信号图像信息与提取后图像信息Fig.8 Image information of observation signal and extracted signal at -20 db 图9 -10 db时,观测信号图像信息与提取后图像信息Fig.9 Image information of observation signal and extracted signal at -10 db 由图6~图9可见,利用变分模态分解算法可有效地使混沌遮掩下混合图像信号实现盲复原,以及加入高斯白噪声也可提取到原图像信息。 本文研究了基于保密传输下单通道图像盲复原问题,提出了一种基于混沌遮掩的变分模态分解实现混叠图像信号的单通道盲复原算法。该算法是利用VMD算法实现对一路混叠图像信号的分解,进而通过FastICA进行重构多维虚拟通道,使其由欠定状态转为正定状态,最后得到原图像信号的估计。计算仿真结果表明混沌遮掩下的单通道图像盲复原可以很好的实现,从而验证了该算法在图像盲复原中具有可行性。由于在实验过程中VMD分解受模态个数k值设定的影响,容易产生过分解或欠分解现象,此外,在噪声状态下实现图像信号盲源分离复原效果未达到理想状态,还需要进一步研究。1 VMD算法实现原理
1.1 变分模态分解
1.2 VMD变分问题的构造与求解



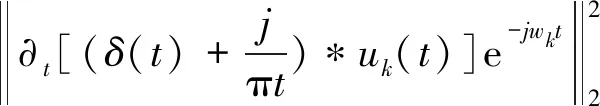

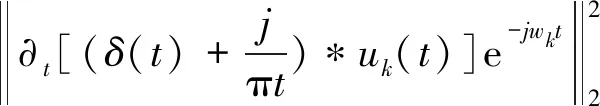

1.3 VMD算法实现步骤


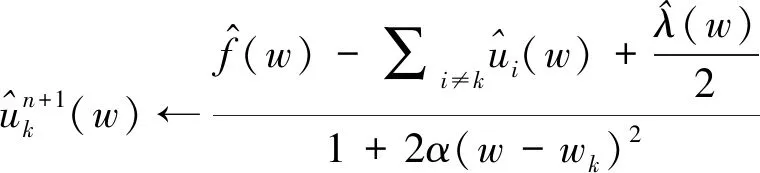
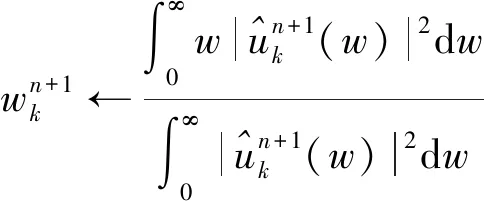



2 图像盲复原实现模型与步骤
2.1 数学模型
2.2 算法步骤
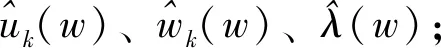
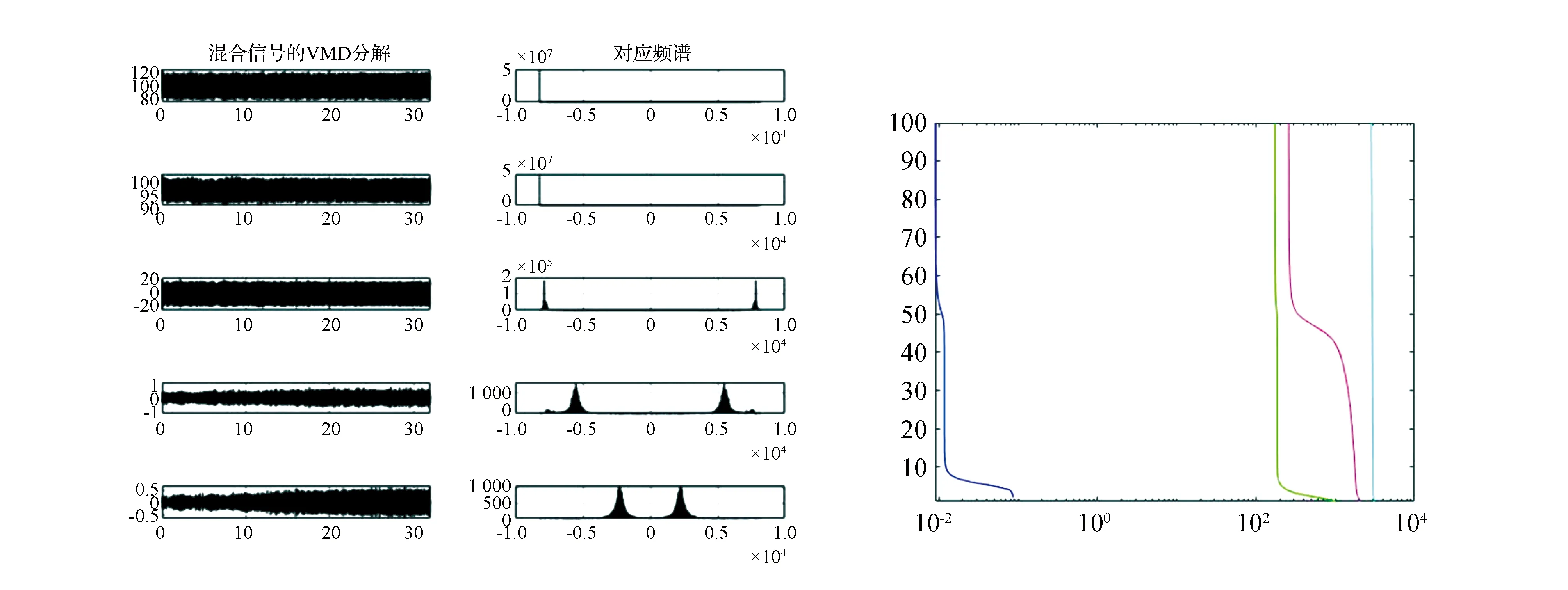
3 仿真与性能分析






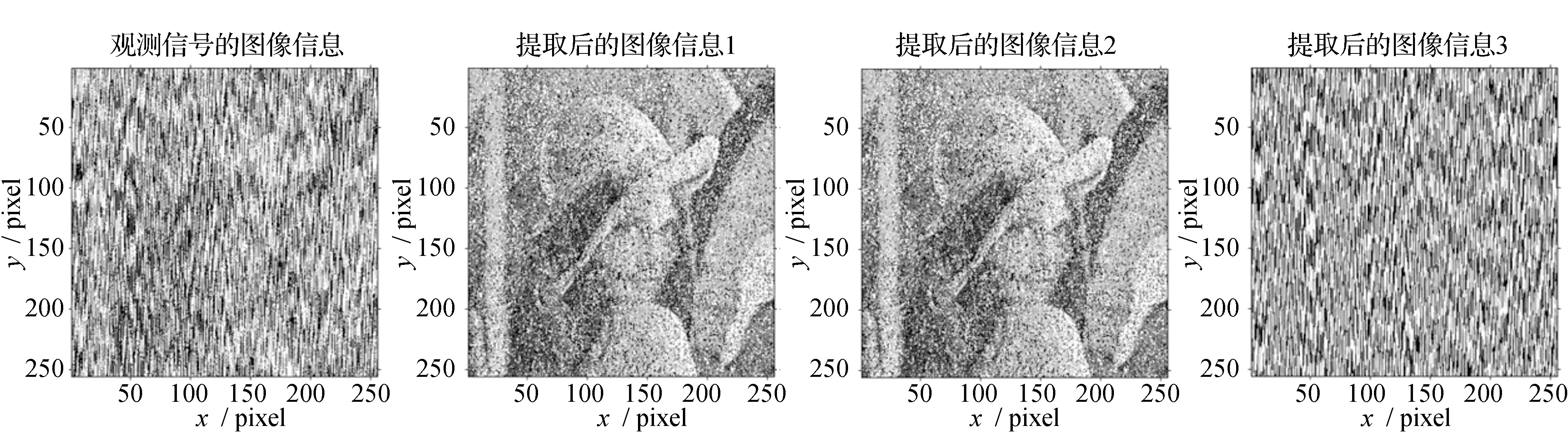
4 结 论
