弱底水碳酸盐岩礁相气藏压裂井试井模型研究
2020-07-14张文昌王海涛
张文昌,王海涛
(1.中国石化中原油田分公司,河南 濮阳 457001;2.西南石油大学,四川 成都 610500;3.油气藏地质与开发工程国家重点实验室,四川 成都 610500)
0 引 言
碳酸盐岩礁相气藏孔隙特征复杂,且常伴有弱底水,底边界无法用定压或封闭底边界条件来进行描述,目前含弱底水的多重介质碳酸盐岩气藏压裂井试井模型还鲜有所见。1963年,Warren和Root[1]建立了著名的Warren-Root双重介质油藏试井模型。不少学者[2-6]对双重介质储层中的渗流及试井问题进行了研究。对于一些孔缝洞均较发育的碳酸盐岩油气藏,双重介质模型已不能对其孔隙特征进行较好的描述,有必要采用三重介质进行描述。1986年,Abdassah和Ershaghi[7]首次提出了裂缝-基岩-溶孔三重介质油藏模型。很多学者[8-20]对三重介质碳酸盐岩储层的试井问题进行了研究。王晓冬等人[21-28]对弱补给底边界问题进行了研究,但只限于均质油藏未压裂直井情形。文中建立了新的弱底水碳酸盐岩礁相气藏压裂井试井模型,模型综合考虑了碳酸盐岩礁相气藏的多重孔隙介质及弱底水相伴特征,同时,实现了求解和渗流特征分析。
1 物理模型
图1为弱底水碳酸盐岩礁相气藏压裂井试井模型,礁相气藏下部与弱底水相连,储层经压裂后形成双翼压裂缝,压裂缝的缝半长为xf。由于礁相储层中孔、缝、洞均较发育,因此,采用三重介质模型描述其孔隙特征。由于存在底水,故储层不全部射开。储层厚度为h(cm),射开厚度为hw(cm)。
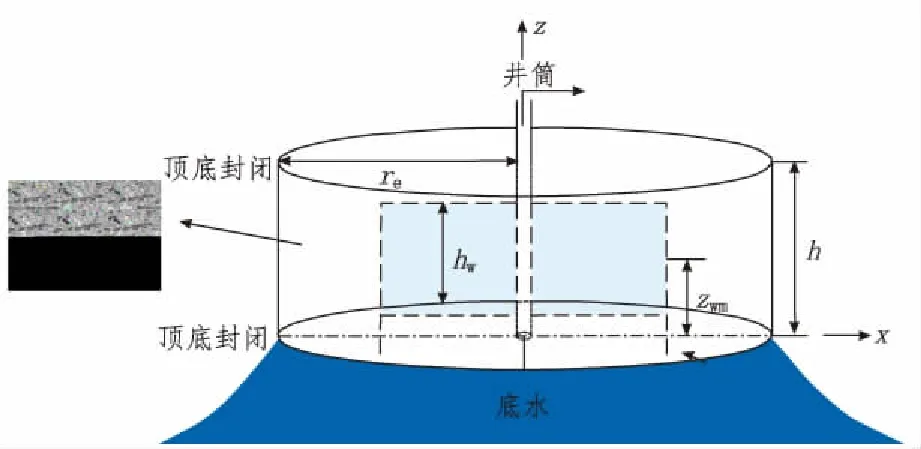
图1 弱底水碳酸盐岩礁相气藏压裂井试井模型
2 数学模型及其解
模型的基本假设如下:①气体在孔、缝、洞3个渗流场内流动满足达西定律;②气井生产前,地层中各点的压力分布均匀;③忽略重力和毛管力的影响;④气体通过天然裂缝流向人工裂缝,再由人工裂缝流向井筒,基质孔隙和溶洞均作为天然裂缝的补给源;⑤存在底水能量补充,但补充有限。
为了建模和求解过程中方程的简洁,模型中的参数采用达西单位制,避免许多冗长的数值常数,而不同单位之间的转换非常简单,在此不再赘述。
根据渗流力学和微分方程理论,建立考虑弱底水部分供给底边界下的孔缝洞三重介质碳酸盐岩礁相气藏不稳定试井模型。
(1)渗流微分方程:
(1)

(2)
(3)
(2)初始条件:
ΨfD(tD=0)=ΨmD(tD=0)=ΨvD(tD=0)=0
(4)
(3)内边界条件(点汇):
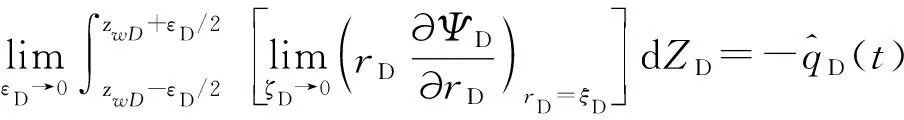
(5)
(4)侧向封闭外边界条件:
(6)
(5)顶部封闭、底部部分供给弱底水外边界条件:
(7)
(8)
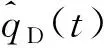
对上述模型采用有限傅里叶有限余弦变换、Laplace变换,运用贝塞尔方程理论求解,可获得点汇解。在此基础上,利用叠加原理,沿压裂缝面z方向(缝高方向)和x方向(缝长方向)积分,可得到
部分供给弱底水碳酸盐岩礁相气藏压裂井的井底压力解:
(9)
其中:
(10)
(11)

(12)
(13)
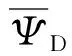
当存在表皮效应和井筒存储效应时,可通过下式来考虑[19-20]:
(14)
3 双对数曲线的渗流阶段及敏感性分析
建立弱底水碳酸盐岩礁相气藏压裂井试井模型,各参数如下(对于有因次量则转换至法定单位下):CD=1,S=0.4,ωf=0.05,ωm=0.75,λv=3.0×10-5,λm=5.0×10-7,h=30m,hw/h=0.3 ,zwm=15m,re=800m,Kfh/Kfv=2,rw=0.1m,xf=10m,θ=0.002。图2为弱底水碳酸盐岩礁相气藏压裂井双对数理论曲线及渗流阶段划分。

图2 碳酸盐岩礁相气藏压裂井双对数曲线及渗流阶段划分
由图2可知,弱底水碳酸盐岩礁相气藏压裂井不稳定渗流可能出现10个渗流阶段:①早期纯井筒存储段,此段拟压力及导数曲线在双对数图上呈斜率为1的直线段;②井储后的过渡段,导数表现为“驼峰”状;③裂缝线性流段,表现为斜率为1/2的直线;④天然裂缝系统拟径向流段,该段反映天然裂缝中的流体流向井筒,基质与裂缝间以及溶洞与裂缝间的压差还未建立,基质和溶洞还未向裂缝发生窜流,导数曲线在纵坐标上的对应的值为0.5(0.5高度水平线);⑤溶洞向裂缝窜流段,反映溶洞与裂缝间的压差已建立,溶洞向裂缝进行窜流,导数曲线呈一个向下的“凹子”;⑥裂缝与溶洞拟径向流段,此阶段溶洞向裂缝窜流达到平衡,裂缝与溶洞压力同步下降,导数曲线又趋于0.5水平线;⑦基岩向裂缝窜流段,反映基岩孔隙与裂缝间的压差已建立,基岩向裂缝进行窜流,该段拟压力导数又呈一个向下的“凹子”;⑧裂缝、基岩和溶洞总系统拟径向流段,此阶段溶洞向裂缝的窜流及基岩向裂缝的窜流达到平衡,裂缝、基岩及溶洞的压力同步下降,拟压力导数曲线又趋于0.5水平线;⑨侧向封闭边界,压力波到达封闭边界后,定产压降时,压力导数曲线向上翘;底水反映段,当底水能量产生影响后,压力导数曲线不再上翘,而变为下掉。
研究各参数对双对数曲线的影响。在分析某参数的影响时,只改变该参数的值,其他参数的值保持不变。
图3为裂缝储容比对双对数曲线的影响。由图3可知,裂缝储容比越小,导数曲线上第一个“凹子”越宽越深。
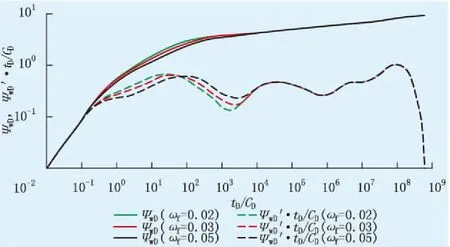
图3 裂缝储容比对双对数曲线的影响图
图4为基质储容比对双对数曲线的影响。由图4可知,基质储容比对压力曲线影响很小,曲线几乎重合,但对导数曲线影响较大,影响2个“凹子”的深浅。基质储容比越小,导数曲线上第1个“凹子”越宽越深,第2个“凹子”越窄越浅。
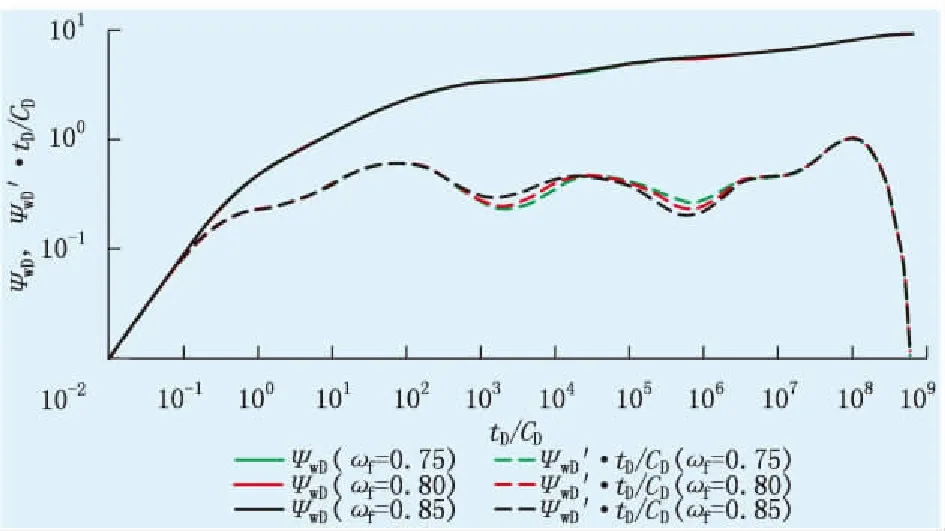
图4 基质储容比对双对数曲线的影响
图5为溶洞-裂缝窜流系数对双对数曲线的影响。由5图可知,溶洞-裂缝窜流系数主要影响第1个“凹子”出现的早晚,λv越小,导数曲线上第1个“凹子”出现得越晚。

图5 溶洞-裂缝窜流系数对双对数曲线的影响
Fig.5 Effect of cave-fracture cross-flow coefficient on log-log curve
图6为基质-裂缝窜流系数对双对数曲线的影响。由图6可知,基质-裂缝窜流系数主要影响第2个“凹子”出现的时间,λm越小,导数曲线上第2个“凹子”出现得越晚。

图6 基质-裂缝窜流系数对双对数曲线的影响
Fig.6 Effect of matrix-fracture cross-flow coefficient on log-log curve
图7为渗透系数对双对数曲线的影响。由图7可知,渗透系数越大,导数曲线上最后1个底水反映段下掉得越早,当θ=0.000时,无底水,此时,压力及导数曲线向上翘,表现出封闭边界的特征。
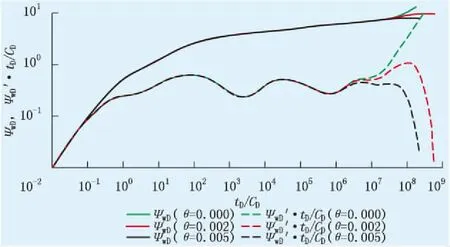
图7 渗透系数θ对双对数曲线的影响
4 模型验证
为验证文中模型的正确性,令文中模型中的θ取一极小的值,如10-10,ωv=0,re→∞,re可取一个很大的值,如109,则模型可简化为常见的顶底封闭、侧向无限大双重介质气藏压裂井试井模型。图8为文中模型的简化模型与Saphir软件计算结果的对比(对比时需将Saphir直接计算的有因次数据进行无因次化),参数取值为:CD=56.085,ωf=0.1,ωm=0.9,ωv=0,λm=1.0×10-7,h=30m,hw/h=1,zwm=15m,re=109,Kfh/Kfv=1,rw=0.1m,xf=60m,θ=10-10。
由图8可知,文中模型的简化模型计算结果与Saphir软件计算结果非常吻合。此外,与国内外诸多商业软件中的模型相比,文中模型能处理更复杂的问题,可综合考虑弱底水、多重介质孔隙特征以及人工压裂的共同作用,适用范围更广。
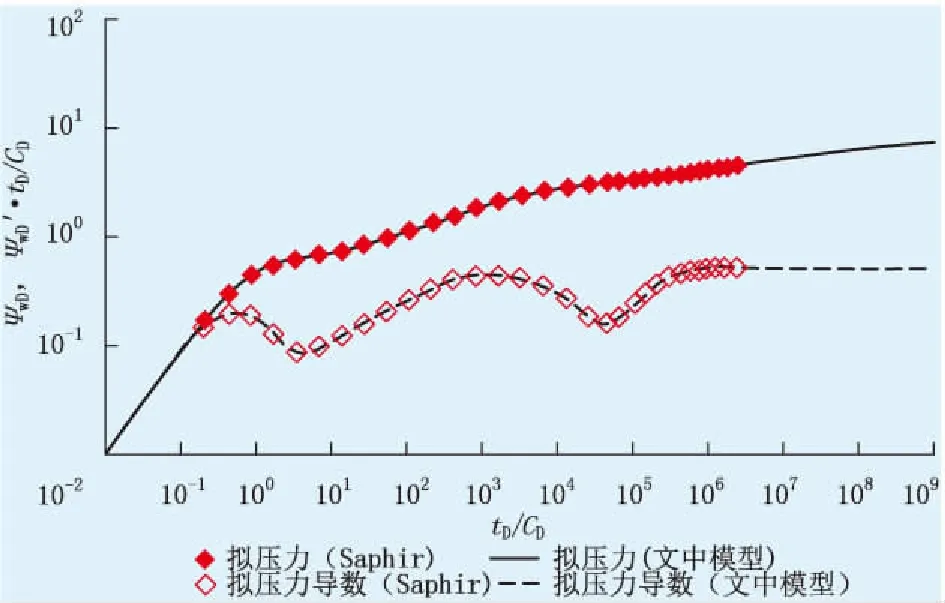
图8 文中模型的简化模型与Saphir软件计算结果对比
5 结 论
(1) 针对目前的试井模型难以描述碳酸盐岩礁相气藏多重孔隙介质及弱底水相伴特征的现状,建立了新的试井模型,在Laplace空间求得了模型的半解析解,弥补了该类气藏压裂气井试井模型的不足。
(2) 曲线特征分析表明,该类气藏理论上可能出现10个不稳定渗流阶段,其中,2个“凹子”是孔缝洞发育的表现,后期曲线下掉是底水的反映。
(3) 裂缝储容比主要影响第1个“凹子”的深度和宽度,基质储容比影响2个“凹子”的深度和宽度;溶洞-裂缝窜流系数、基质-裂缝窜流系数分别影响第1个“凹子”和第2个“凹子”出现的先后顺序;渗透系数的大小反映了底水强弱,渗透系数越小,底水越弱,导数曲线下掉的时间越晚。
