投贷联动、系统风险与资本顺周期效应

黄柏翔 何恭政 彭红枫

(1.清华大学 五道口金融学院，北京 310027；2.中南财经政法大学 金融学院，湖北 武汉 430073；3.山东财经大学 金融学院，山东 济南 250014)

一、引言

投贷联动试点是2016年《政府工作报告》中金融驱动创新发展的重点工作，主要希望银行通过子公司或者与私募股权投资(PE)、风险投资机构(VC)协同合作，对目标公司进行股权投资；配合贷款支持，围绕不同成长阶段企业的直接与间接融资需求，既是提供创新型一站式综合金融服务，也是推进金融与实体经济供给侧改革的举措。对于银行来说，投贷联动风险可分为以下两个方面：一是事前与事中贷款的信用风险与投资的市场风险，二是必须具备有效的资本市场融资、定价、退出机制，缓解银行投融资事后的退出风险。

与已往市场风险衡量明显差异的是，投贷联动投资核心是支持种子期、初创期、成长期的科创企业，有极大概率为非上市公司，银行将面临无法明确观察到市场交易价格的困难，新创公司的价格受公司能否存活的信用风险影响更高。因此，借鉴巴塞尔银行监管委员会(Basel Committee on Banking Supervision，BCBS)2016年1月提出的最新市场风险最低资本要求的终稿，本文采用Basel 3.5投资与贷款行为都需面对的共同风险因子——资产相关性系数作为研究指标。

此外，不同的直接融资渠道的导入是投贷联动事后退出的关键，尤其是当资本市场参与者越多，即市场具备了更多的流动性时，能否真正减少银行持有的股权或退出的违约风险也是本文关注的另一个问题。例如，股权分置改革是我国资本市场的一个重大举措，当消除非流通股和流通股的流通制度差异之后，企业有更多的权益在市场流通，这可能降低其杠杆水平进而减少违约风险[1]。因此，本文讨论股权分置改革前后违约风险的变化，对于回答多层次资本市场的建设能否切实协助投贷联动进而达到缓解风险的目的，有一定的借鉴意义。

本文的主要贡献有以下两点：一是基于Basel 3.5的最新监管准则，通过构建基于市场权益价格的高级内部评级法求出资产相关性系数，探讨投贷联动时系统风险与银行资本的关系。这种从市场权益价格出发的视角更能符合Basel 3.5希望真实反映市场变化的要求。二是通过分析股权分置改革前后系统风险的变化，同时考虑投贷联动的事前、事中与事后的风险管控。研究发现，有效落实支持小微企业创新的投贷联动，同时完善多层次资本市场等配套措施，可以有效降低商业银行系统风险冲击，缓解经济下行时银行资本要求的顺周期性。

二、文献评述

随着信用风险内部评级法的最新要求不断出台与完善，对于最重要的预期损失，巴塞尔银行监管委员会(BCBS)采用ASRF模型，分别以个别企业违约概率与资产相关性系数作为衡量非系统性风险与系统风险因素的基础，将两者相结合进行评估。两者数值越高将导致预期损失增加，进而需要满足更高的资本要求。其中代表系统风险的资产相关性系数更是多样化投贷组合下所需考虑的重点。然而，现阶段银行使用ASRF模型进行评估面临下列三个关键问题: 其一，与投资相关的市场风险需要考虑相同的违约贴水内部评级法[2]，并要求反映真实的市场情况。例如，资产相关性系数必须由信用价差或者市场权益价格计算而出，与过去信用度量组合模型 (credit metrics) 的信评矩阵估算有所差异。其二，预期损失必须充分反映债务人的风险特征及行业特有变量等因素。例如，资产规模较大的企业具备多元化经营的优势，但对不可分散的系统风险是否具有较高的敏感度并不清楚，故不同企业资产相关性系数的风险特征可作为投贷配置的参考依据。其三，ASRF模型是否具备合理性。假设引入系统风险的资产相关性系数存在顺经济周期现象，即预期损失会随着经济周期的下行而反向增加，造成投融资紧缩，进而导致经济加速下行，这与银行稳健经营的原则明显相悖。

通过研究代表系统风险的资产相关性系数与其特有的风险特征的相关文献可知，风险特征主要分为违约概率、资产规模与行业形态等三类。例如，巴塞尔银行监管委员会依照不同的公司规模与形态将资产相关性系数进行分类计算，公司销售额越低，则资产相关性系数越小，具有越高的资本节约效果。Lee等人(2011)发现资产相关性系数与公司规模呈正相关，这表明大公司受系统风险影响较显著[3]。Dietsch和Petey (2004)进一步验证大型企业因为多元化程度较高，对于系统风险也具备较高的敏感度[4]。Chan等人(2007)则认为应将产业特征与公司规模视为两个独立因素，虽然中小型企业的平均违约概率高于大型企业，但在不同产业中(如制造业、汽车业与建筑业)，中小型企业的资产相关性系数更容易受到系统风险因素的影响[5]。

此外，ASRF模型中的基础内部评级法并未探讨资产相关性系数的变化是否源自宏观周期的影响。有学者发现宏观经济衰退时，资产相关性系数有随之上升的顺周期现象，此时将造成银行预期损失增加，进而导致信贷业务或者投资头寸紧缩，市场上的公司因此将无法顺利获得流动性，最后导致自身违约率上升；在如此恶性交互影响之下，实体经济只能走向衰落，这被称为资产相关性系数的顺经济周期特征[6]。Duffie等人(2007)的实证研究显示当经济下行时，企业违约概率确实会随之增加[7]，Lee等人(2011)则发现资产相关性系数同时存在顺经济周期特征和不对称效果，即经济下行时资产相关性系数的上升幅度更高，从而导致低估低迷时期的监管资本[3]。此外，除了衡量贷款组合信用风险的资产相关性系数外，权益市场的资产相关性系数也存在顺周期现象[8]，亦发现债券市场当经济繁荣时，违约状况会有较低的顺周期现象[9]，显示资产相关性系数的周期特征将同时影响信用与市场风险的度量。

我国探讨信用风险、资产规模与行业形态的文献也较丰富。章彰(2011)以我国香港金管局内部评级法为例[10]，发现公司敞口必须区分为大企业与中小企业，同样的违约概率下选择中小企业将会有一些资本节约优势；杨继光与刘海 (2009)指出信用风险最主要的就是行业集中风险，这尤其体现在高度相关的信贷资产组合之间[11]；马勇等(2009)同样认为行业风险是影响经济资本的重要因素之一[12]。在预期损失与经济周期特征研究方面，王胜邦与陈颖 (2008)认为资本要求存在顺周期性，体现在商业银行的内部模型低估了经济下行期的违约率[13]；孙岩与汪翀 (2011)则提出，在对与违约概率相关的风险进行调整后，资本收益率 (RAROC)同样具有经济顺周期的特征[14]；王力伟等(2012)也发现在不利的经济状况下，违约概率和损失率往往会同时增加，这会导致在一定置信度下更高的在险价值(VaR)[15]。此外，近期相关研究也发现商业银行的信贷运行与经济周期间存在很强的顺周期特征[16][17]，因此随着经济起伏，银行收益与风险将具有较高的周期性波动。

然而，现有国内文献的讨论主要聚焦在新资本协议的进程[18][19]、资本节约、评级体系与集中度管控等问题，缺乏立足于高级内部评级法对我国不同公司形态、规模与资产相关性系数现状的思考以及涵盖投贷联动中的市场与信用风险的探讨。同时，虽有文献讨论我国信贷发放、RAROC、VaR与经济周期间的关系，但大多数文献关注的是个别企业的违约概率，忽略了无法分散的系统风险，而从近期的风险事件可发现银行乃至整个金融业面临的宏观系统风险逐步加大，有必要重新审视投贷联动下系统风险与经济周期间的关系。

三、理论模型构建

(一) 内部评级法中资产相关性系数

在衡量信用风险以及市场风险的最低资本要求时，为避免低估经济周期带来的外部宏观风险，BCBS加入了资产相关性系数以真实反映系统风险。首先定义X代表系统风险 (systematic risk) 衡量因子，为了让银行具有充足的资本来应对经济下行，将X设为能覆盖99.9%置信度，即尾端极端情况下的系统风险值。通过内部评级法，银行可以估计每笔贷款组合的条件预期损失 (conditional expected losses, CEL) ，如式 (1)：

CEL=P[D=1|X=χ99.9]×E[L|D=1,X=χ99.9]

(1)

式(1)中，P[D=1|X=χ99.9]为0.1%显著性水平下的条件违约概率 (conditional default probability, CDP)，E[L|D=1,X=χ99.9]为相同情形下的条件违约损失率(conditional loss given default, CLGD)，D等于1则发生违约，0则无违约，式 (1)中的预期损失越高将提备越多的信用与市场风险资本。BCBS利用ASRF模型估计式 (2) 中的条件违约概率[20]:

(2)

式(2)中，N(·)为累积正态分布函数，N-1(·)为其反函数；PD是贷款组合违约风险的非系统性违约概率，反映贷款组合中债务人的特定风险；N-1(0.999)则代表极端的经济状况；ρ定义为资产相关性系数，代表与宏观经济形势相关的系统风险，进而正向影响条件违约概率(CPD)与条件预期损失(CEL)。尤其当银行可通过持有大量贷款组合来分散非系统风险时，无法分散的系统风险是影响ASRF模型中预期损失最重要的因素之一，亦是本文探讨的重心。同时，巴塞尔银行监管委员会(BCBS, 2004)的基础内部评级法为产业提供了不同的计算资产相关性系数的方法，估计如式 (3)：

(3)

由式(3)可知，巴塞尔银行监管委员会假设系统风险仅与违约概率相关，而且当违约概率较高时，表示对贷款组合的影响将比系统风险更高，资产相关性系数(系统风险)与个别企业违约概率(非系统风险)两者呈现反向关系。然而，BCBS (2016)在利用内部评级法求得风险资本要求时，认为资产相关性系数要能反映真实市场情况，而非仅仅由历史数据统计出来的违约概率[2]。因此，本文引入与市场权益价格相关的违约概率与资产相关性系数模型，并验证两者是否同样呈现负向关系，作为高级内部评级法模型是否符合本文基础内部评级法的假设检验评估。

(二) 高级内部评级法中资产相关性系数

BCBS (2016)在利用ASRF模型求得风险资本要求时，尤其在估计投资中的违约风险时，所使用的模型要能反映真实市场变化，就必须建立在信用价差或市场权益价格的基础上[2]。遵循这个概念，本文首先利用Merton模型估计违约概率，以权益价格为基础来满足BCBS (2016)的要求[2]。如果将贷款标的公司信用状况看成以资产为标的的欧式期权，负债则设为履约价格，当债务到期，资产小于负债时，公司股东将选择不履约而导致违约发生。假设资产价值符合式 (4) 的几何布朗运动:

(4)

式(4)中，V是公司的资产价值，μA是资产收益期望值，σA是公司资产收益的波动率，Z是几何布朗运动。在风险中立测度下公司的权益市场价值E为式 (5) :

E=VN(d1)-e-rTDN(d2)

(5)

式(5)中，D为公司在T时点到期的负债，r为无风险利率，N(·) 是累积正态分布函数。其次，利用伊藤引理 (Itō's lemma)，可以推导出公司权益价值波动率(σE)与公司资产收益波动率间关系，并列于式 (6) :

(6)

通过式(5)和式(6)求解非线性联立方程式，可得到企业隐含的资产价值(V)以及资产收益的波动率σA。N(-d2) 则为风险中立测度下的违约概率(PD)。为符合BCBS (2016) 要求，风险资本计算需依靠真实测度下的违约概率，本文借鉴Lee等(2011)估计的μA结果[3]，将N(-d2) 转换为具有真实测度下的违约概率。

其次，早期的文献大多使用穆迪的KMV模型或是信用矩阵估算高级内部评级法下的资产相关性系数，与BCBS (2016) 认为ASRF模型必须以信用价差或权益市场变化为基础的概念不一致[2]。本文利用Lee等人(2011)的推导结果[3]，由权益(E)与市场(M)信息出发求得资产相关性系数(详见式7)，这更能反映真实市场变化情况。

(7)

式(7)中，βE为权益的系统风险，σM为市场收益率波动率。

四、样本设定与描述性统计

(一) 样本与变量设定

本文经济周期数据源于中国统计局，克强指数(Li keqiang index)源于国家能源局，产业分码源于DataStream数据库，市场利率源于人民银行，财务指标则取自国泰安数据库(CSMAR)。研究期间为1995～2013年，研究对象以我国上市企业为主①。为保持年化数据的完整性，排除每年日交易数据少于100笔的企业，且进一步要求样本序列必须连续5年，以提高资产报酬波动率估算的准确程度。此外，对于没有负债的企业，因不符合违约概率计算需求，故予以排除。最后，19年间样本共有14825个企业，依照全球产业分类码(Global industry classification, GICS)与DataStream数据库内的INDC产业分码，将样本内企业区分为: 材料业、消费品、保健、工业、服务业、石油品、信息业、电信业、公用事业与金融业等10个产业，无风险利率则使用一年期政府公债利率。

(二) 描述性统计

表1列示了年化描述统计量，由式 (2) 中可得知资产相关性系数代表系统风险相关程度，同时与预期损失呈正比。式 (9) 则显示资产相关性系数主要取决于企业的三个特征: 一是资本市场上的权益系统风险βE；二是权益价值与企业资产价值比值 (E/V)；三是市场与资产收益波动率比值。因此，当企业自身的权益系统风险βE越高且资产规模V与波动率σA两者越小时，资产相关性系数将会越高，其预期损失将容易受外在经济周期的系统风险影响，对于投资与放贷需要更多的资本补充。表1显示我国在2006年实施股权分置改革后，资本市场有了结构性改变，虽然βE平均上升了5.85%②，但在资本市场逐步发展后有利于企业成熟发展，平均资产规模与波动率两者皆有较大幅度上升，分别为4.05倍与14.32%③，系统风险因此降低④，进而减少预期损失与监管资本要求。

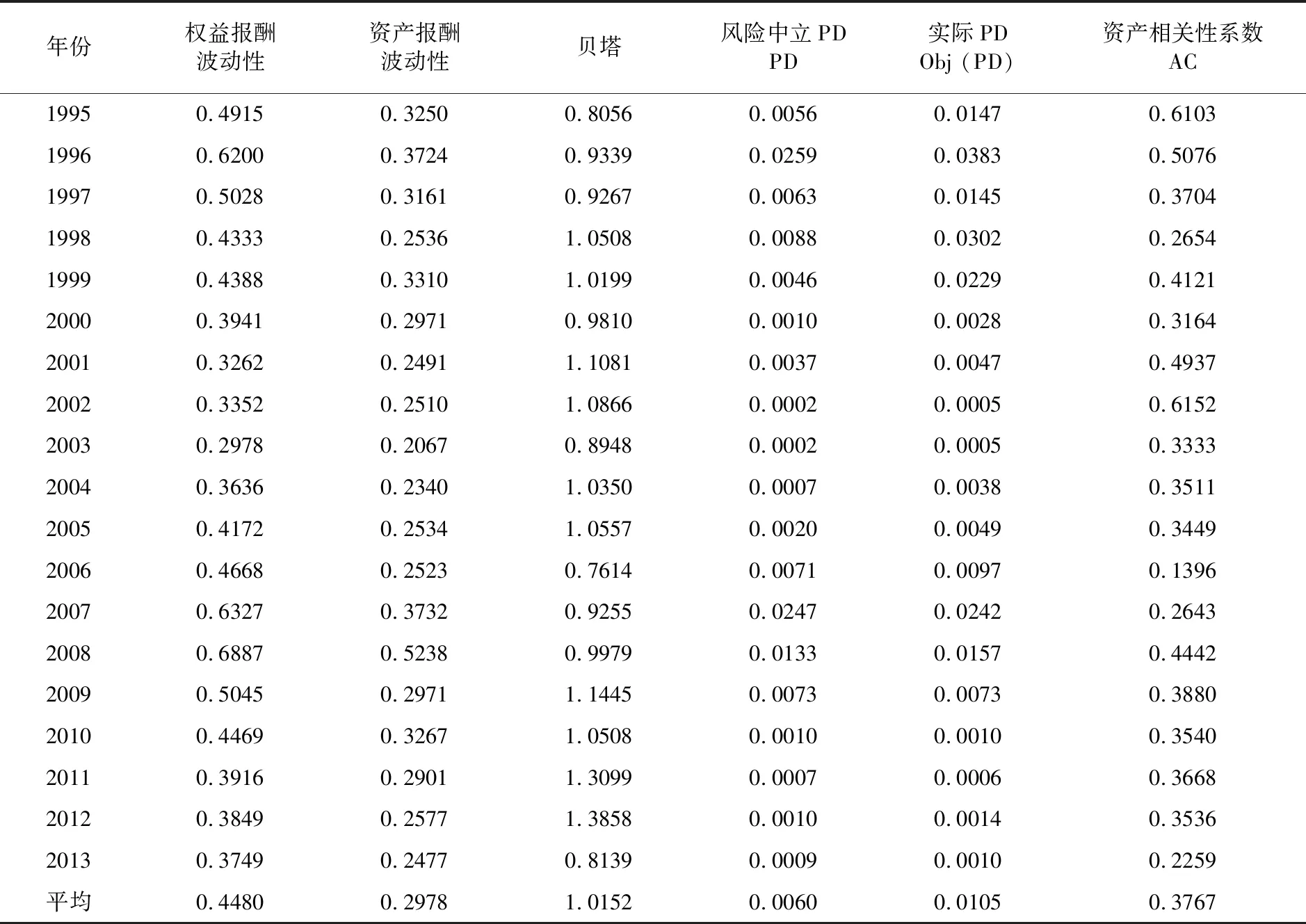
表1 我国企业14825个截面数据描述性统计量

此外，股权分置改革后的资产相关性系数，除了2007年受全球金融风暴影响而上升外，整体有逐渐下降的趋势，2013年下降至22.59%，对照新资本协议(Basel II 以及Basel III)的资产相关性系数位于12%～24%间(由式(3)可知)，当企业发展逐渐成熟时，我国资产相关性系数将逐步符合国际要求水平。因此，投贷联动如果能够通过商业银行支持实体经济成长，同时健全多层次资本市场，在企业健康发展时，系统风险影响趋缓、投贷预期损失下降与资本要求降低，对商业银行发展都有相当程度的帮助。

五、实证结果分析

(一) 违约概率、资产相关性系数与企业规模

依据银监会内部评级法的要求，下文讨论资产相关性系数与个别企业运营规模间的关系。首先以违约概率与资产相关性系数建立回归模型，再加入企业规模效果分析。回归计量模型皆采用面板数据模型，具体使用最小二乘法(OLS)，并分别控制年度效应或行业效应。式(8)首先检验资产相关性系数与企业规模是否呈现统计上的显著关系：

(8)

式(8)中，ACi,t为i企业在第t期的资产相关性系数，PDi,t为违约概率，SIZEi,t为营业额取自然对数，DYy为第y年虚拟变量。此外，由于营业额为自然对数形态，我们再加入资产相关性系数的自然对数与现实违约概率(假设非风险中立时)作为变量，重新验证回归结果的稳健性。

表2 企业规模特征对于资产相关性系数回归结果

注：*、**和***分别表示参数估计在10%、5%和1%的水平下通过了显著性检验。下表同。

表2显示一般资产相关性系数(回归(1)到回归(4))或是logistic调整的ILnAC⑤(回归(5)至回归(8))，两种违约概率在加入公司规模变量LnSalei,t前后，对于资产相关性系数影响方向与显著性不变，负向效果也与巴塞尔银行监管委员会要求一致，显示系统(AC)与非系统风险(PD)两者具有权衡(trade-off)效果，高系统风险相对企业的违约风险较低，这也说明讨论公司规模对于资产相关性系数影响，将不受违约概率干扰而造成偏误。

其次，从表2发现资产相关性系数与企业规模(加入后为回归(3)(4)(7)(8))呈现正向显著关系，即大公司的资产相关性系数会高于小公司。拟合度(Adj. R2)则维持在27%～35%，说明大公司的资产相关性系数越高，在宏观系统风险增加时，投贷预期损失将会越高，反而使银行付出越多资本，小企业由于经营的灵活性，受宏观周期相关系统风险较小。因此，通过投贷联动扶持越多中小企业，将可以减少我国商业银行在经济周期下行时的系统风险。

(二) 资产相关性系数与产业特征

为深入了解产业特征对于资产相关性系数的影响，同样首先对照加入产业变数前后违约概率、企业规模与资产相关性系数三者间的关系是否会改变，式 (9) 为增加产业特征后的回归：

(9)

表3显示控制不同产业特征前后，DIj为新加入的j产业的产业效应，无论违约概率或是企业规模对资产相关性系数的影响方向并没有改变，同时产业系数显著性水平皆达到1%，因此，不同产业对于资产相关性系数确实存在显著的影响效果。

确认产业对于资产相关性系数存在显著影响后，表4列示个别产业的平均资产相关性系数⑥与产业相关系数。美国专门从事投贷联动支持的硅谷银行以销售收入规模作为判断企业成长周期的主要指标，例如替500万美元以下的初创企业提供孵化融资服务，占整体借款比重50%以上，因此，本文将销售收入作为另一个产业特征分类指标。与上文结论相似，销售收入最小的3个产业: 通信业(0.2182)、医疗生物技术(0.3000)与电子制造业(0.3184) 拥有最低的资产相关性系数，再次证明如要减少投贷联动中的系统风险，中小企业与产业将扮演关键角色。

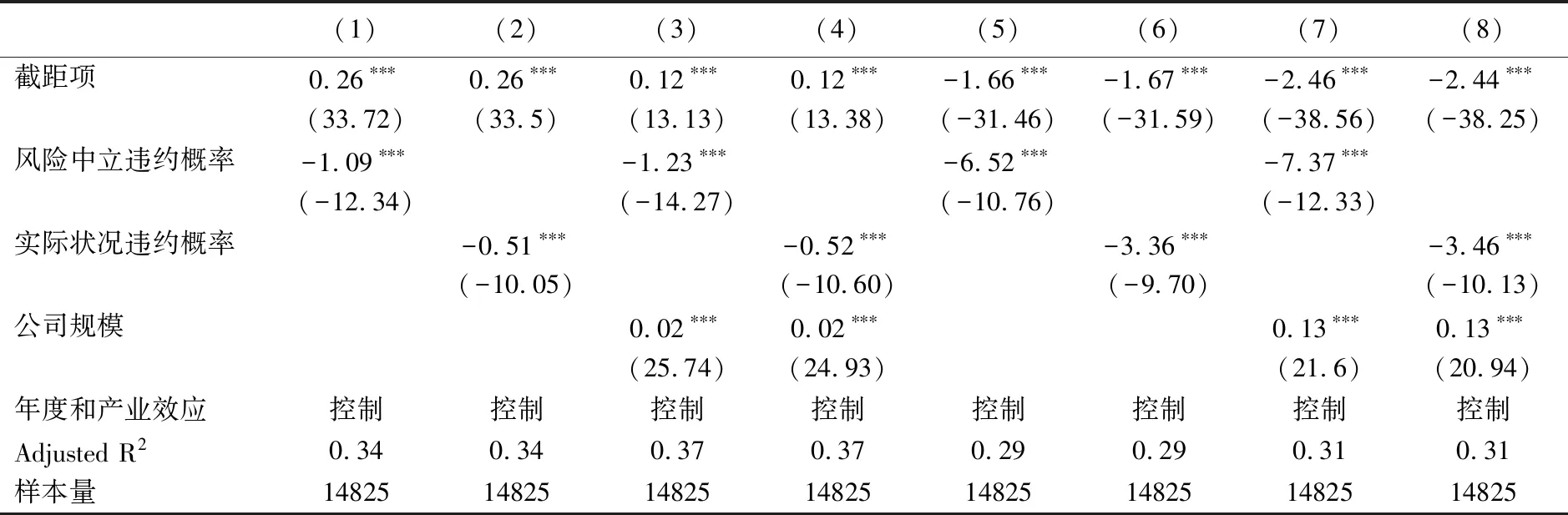
表3 产业类型特征对资产相关性系数回归结果

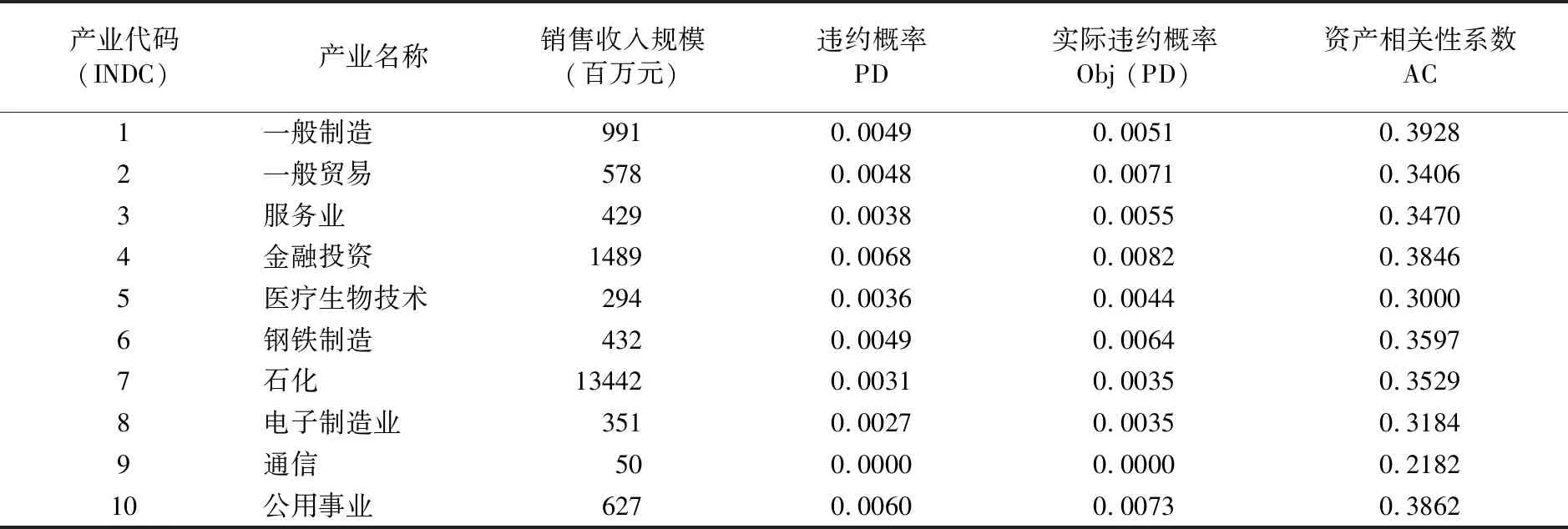
表4 个别产业类型资产相关性系数

(三) 资产相关性系数与经济周期特征

银行顺周期效应指的是经济繁荣时期较低的预期损失使投贷等风险性资产大幅增加，在经济过热时反而积聚更多的系统性风险；当反转到萧条时期时，大量资产减值损失导致资本充足率、投贷能力降低，使原本恶化的经济状况雪上加霜。为了探究资产相关性系数对银行顺周期行为的影响，本文参照中国统计局发布的经济周期性变化期指标，以绿蓝灯与蓝灯期间作为经济周期下行评分标准，并且将实际国内GDP增长率(the Growth rate of real Gross Domestic Product，GGDP)与经济周期性指标相互交乘，观察在GGDP变动下，式(10)是否存在非对称效应：

(10)

式(10)中，GGDPt为t期国内生产总值成长率；DrGGDPt为国内生产总值成长率与经济周期性变化期指标的交乘项。如表5所示，无论在GDP成长率或者是DGGDP中与经济周期性变化期指标的交互影响，皆显示宏观变数对于资产相关性系数存在显著的经济顺周期现象。举例来说，当经济周期不佳时，除了GDP成长率下降1%，资产相关性系数增加0.07%外，两者交乘项也会贡献0.06%，总资产相关性系数会上升0.13%，具有预期损失加速升高的不对称效果，银行必须提出更高的资本要求。

此外，有部分学者认为我国债务杠杆率过高，相当一部分表现在工业企业。为了增加经济顺周期效应的稳健性测试，本文利用预测工业企业利润增长的克强指数作为GDP成长率的另一个代理变量。实证结果显示，无论克强指数或者是交互影响项(DKeqiang index)皆显著为负，表示资产相关性系数确实存在经济顺周期现象。因此当工业周期下行时将会增加资产相关性系数，进而使投贷预期损失与资本损耗上升，造成银行业体系不得不紧缩贷款，加速“三去一降一补”中的“去杠杆”效应发生。

表5 经济周期特征对于资产相关性系数回归结果——以经济周期性变化期指标为例

为了更进一步证明股改前后资产相关性系数是否有显著差异，本文将时间虚拟变量调整成1995～2015年为0，2006～2013年为1，重新验证表2、表3与表5中的所有回归模型，结果发现：一是违约概率对资产相关性系数的影响保持为负，符合巴塞尔委员会对于模型的基本假设；二是资产规模、产业变量与经济周期等因子的影响方向保持不变，保持前述资产相关性系数所有特性；三是所有回归的时间虚拟变量皆显著为负，代表股改后(2006～2013年)的资产相关性系数确实较低，银行放款与投资在股权分置改革后面临了更低的系统风险(受限于篇幅，仅列出实证分析结果)。

六、结论与政策建议

基于巴塞尔委员会于2006～2016年公布的信用与市场风险高级内部评级法，本文利用其中的共同风险参数——资产相关性系数，分析我国商业银行开展投贷联动所面临的违约风险。资产相关性系数联结投贷时的违约损失及系统风险因子，进而影响监管资本、利息收入与拨备计提，是未来完善投贷联动资本战略配置与监管政策可参考的重要参数之一。本文构建以市场权益价格为基础的资产相关性系数，除满足Basel 3.5的高级内部评级法的规范外，从事前、事中的信用与市场风险评估，及事后资本市场退出等风险管控视角，进一步分析了股权分置改革前后的资本市场、个别企业规模、不同产业及经济周期等四个特征与系统风险间的关系，并根据结果提出以下建议:

第一，我国应进一步完善投贷联动的风险管理与资本计提机制，也可以依据较低的资产相关性系数与系统风险调降中小微企业的风险权重，从监管层面为金融驱动小微企业创新提供技术层面上的支持。

第二，支持中小企业虽能减少系统风险，但在资产相关性系数与个别企业违约概率呈负相关的结果时，将面对较大的非系统风险。因此，我国应逐步推进2015年8月《推进普惠金融发展规划(2016～2020年)》提出的国家融资担保基金，或者借鉴英国的中小企业成长基金经验，由政府或者行业协会牵头，协助成立更多的商业银行风险共摊机制，减少非系统风险带来的损失，这些措施对于投贷联动的可持续性与风险管理将提供更多的体制机制保障。

第三，我国资产相关性系数存在经济顺周期与不对称效应，从新资本协议的视角分析，如果投贷联动集中在较大规模的企业或产业，较高的资产相关性系数将会造成我国银行在经济下行周期时需要更多监管资本，导致往后投资与放贷更加紧缩，如此压力下将使去杠杆效应更甚，同时造成银行“雨天收伞”的顺周期现象，同时导致收益与拨备的高波动性。这表明积极完善中小企业与产业的投贷联动政策，可以有效缓解经济下行时，较大规模的企业或产业带给银行高预期损失的风险，进而降低市场与信用风险的资本要求顺周期效应。

第四，股权分置改革后的资本市场结构改变，使银行放款或投资的资产相关性系数显著缩小，主要体现在企业平均资产规模与波动率的增加。而在企业发展逐步成熟之后，联结系统风险的资产相关性系数逐年降低，符合目前国际监管要求水平。因此，我国未来在实施投贷联动试点同时，除了商业银行对接不同投资机构之外，更需要积极对接主板、创业板、新三板等多层次的资本市场。除了完善投贷联动有效的退出机制和提供企业一站式的综合金融服务需求外，从风险管理的角度来看，健全多层次资本市场带来的企业规模增加效应，可以减少投贷联动的系统风险，亦可协助商业银行降低高违约概率所带来的资本损耗。

注释：

①若投贷联动相关的未上市企业缺少权益价值波动率等参数，参照KMV公司将未上市企业的税息折旧及摊销前利润(EBITDA)除以资产作为指标，再与相似地区与产业的上市公司对标，最终利用私人企业模型(private firm model)推测出未上市公司的违约概率参数。

②资产相关性系数的平均值由1995～2006年的0.42变为2007～2013年的0.32，下降了23.81%。

③资产价值平均值由1995～2006年的3.24亿美元增加至2007～2013年的16.4亿美元；波动率则由1995～2006年的28.09%上升至2007～2013年的32.11%。

④权益系统性风险值平均值由1995～2006年的0.991变为2007～2013年的1.049。

⑤因资产相关性系数其系数界于0到1之间，本文为了使应变量与自变量之间不要有太大差异，因此对资产相关性系数做logistic调整。

⑥根据新巴塞尔协议二 (Basel II) 规定，本文选取销售营业额作为公司规模代理变量。此外，为了检测代理变量是否具备稳健性，本文重新利用权益价值作为公司规模代理变量实证，结果发现无论用销售营业额或是权益价值当作代理变量，其结果一致。