圆管带式输送机起制动的动态特性及其混沌特征

周广林， 郭延超， 吴 卿， 成云飞

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

圆管带式输送机作为一种新型的高效环保散料运输设备，随着现代工业技术的不断发展，对其动态性能及系统稳定性的要求越来越高，传统的静态设计方法已不能适用其日益增长的要求[1-2]。输送机运行过程中，存在着各种形式的振动，其中起动和制动过程尤为明显[3-4]，输送机在起动、制动过程中，由于输送带的黏弹特性以及驱动装置的控制方式不同，输送带张力、速度和加速度存在延时性，同时输送带的张力和带速变化过大容易产生大的冲击，产生惯性载荷，形成张力波，导致输送带张力分布不均匀，造成输送机振动，运行不稳定[5-8]。目前，相关学者对带式输送机动态系统的研究主要从动力学模型、输送机的起动制动方式、张紧装置布置与设计、输送带参数、横向纵向振动等特性方面进行了研究[9-13]，周广林等[14]基于分形维数对大型带式输送机的动态特性进行了研究，指出系统分形维数越大，系统越不稳定，故障率越高。带式输送机动态特性分析虽然有一定的研究基础，但输送机系统定量分析研究不足，因此，笔者基于AMEsim软件建立圆管带式输送机动态仿真模型，分析不同起动制动时间下输送带张力的变化特性，应用混沌理论，研究不同起动制动时间下输送机系统的稳定性。

1 仿真模型

选用单圆管型圆管带式输送机作为研究对象，输送机型号为DG350，采用重锤式张紧方式[12]，输送距离1 200 000 mm，管径350 mm，生产能力800 t/h，输送带带宽1 400 mm，输送带厚度17 mm，驱动滚筒直径1 000 mm，改向滚筒直径800 mm，托辊直径159 mm，承载段托辊组间距1 500 mm，回程段托辊间距2 000 mm。

输送带的黏弹性模型选用非松弛模型，非松弛模型也称为Kelvin-Voigt固体黏弹性模型，是目前广泛应用的输送带黏弹性模型，其由一个弹性子模型和一个黏性子模型并联组成。

非松弛模型中两个子模型的应变相同，模型总应力为两个子模型的应力和，其本构关系为

式中:σ(t)——动应力，MPa；

ε(t)——动应变；

E——弹性模量，MPa；

η——黏性系数，MPa·s。

根据圆管带式输送机工作原理以及输送带黏弹性特性，在AMESim软件的机械库和信号控制库中选择合适的元件，将各部件对应的模型元件按建模需要进行有序连接，以外置重锤式张紧布置方式为例，搭建一个单驱动的圆管带式输送机虚拟模型，模型示意如图1所示。

图1 圆管带式输送机虚拟模型Fig. 1 Virtual model of circular tube belt conveyor

圆管带式输送机起动制动时，由于其特殊的输送带布置方式及物料输送方式，加速度过大或加速度突变明显，会影响其整体稳定性。分析起动制动过程的速度、加速度变化得出圆管带式输送机的动态特性，选用合理的速度控制方式。圆管带式输送机的速度控制能够提高运输效率，降低驱动装置的能耗，基于澳大利亚的Harrison博士提出正弦驱动曲线分析圆管带式输送机起动、稳定运行、制动过程的动态特性[15]，其速度控制方式为

式中：v0——圆管带式输送机稳定运行速度，m/s；

t1——起动时间，s；

t2——稳定运行时间，s；

t3——制动时间，s。

2 混沌特性

2.1 混沌特性验证

圆管带式输送机是一种复杂的非线性系统，由于输送带具有复杂的黏弹性特性，其振动特征信号为非线性， 圆管带式输送机的振动信号为一维时间序列信号，对于给定的时间序列，如果不能对时间序列的混沌特征做出准确判断，就无法用混沌方法来研究时间序列，如若不加以判断，盲目套用混沌理论方法，将无法保证结论的真实性与准确性。由于混沌系统在某种意义上具有自相似性，因此，往往会采用分形几何学的方法对混沌系统进行描述，其中关联维最具有代表性，它能够定量地描述系统的复杂程度[11]。

传统的G-P算法是Grassberger和Procaccia于1983年提出的，是一种从时间序列计算吸引子关联维数的一种算法[16]。由向量集{Xj|j=1,2,…,p}的p个向量中任意选一个基准向量Xi，计算其余p-1个向量至Xi的距离

对所有的Xi(i=1,2,…,p)重复这一过程，得到关联积分

式中：θ(u)——Heaviside函数，θ(u)={1,u≥0;或0,u<0}；

ε——无标度观测尺度。

在ε→0的过程按照费根鲍姆常数α衰减，即

(1)

当ε充分小时，式(1)逼近下式

lnCm(ε)=lnC+D(m)lnε，

则相空间Rm中的关联维D2可以表示为

在实际应用中，常通过按费根鲍姆常数衰减无标度观测尺度，绘制lnC(ε)∝lnε曲线，对其进行直线拟合，直线斜率即为所求相空间的关联维，通过计算关联维可对系统的运动状态分类。

2.2 G-P算法计算K熵

Kolmogorov熵(K熵)是表征系统无序程度的重要测度，反映了系统的混沌程度，代表了系统信息的损失程度。

(2)

两边同时取对数有

(3)

对充分大的相空间维数以及充分小的无标度观测尺度ε，当D2不再变化时，有

式(2)减去式(3)可得

K熵可以定量描述非线性系统的稳定性，当K熵值大于零时，系统作混沌运动，K熵值越大，系统的混沌特征越明显，系统越不稳定，故可通过计算输送带张力的K熵值，来评价圆管带式输送机系统，输送带张力的K熵值越小，圆管带式输送机系统的稳定性越高。

3 仿真结果与分析

圆管带式输送机随着输送距离和运行速度的增加，其动态特性对输送机的安全运行影响变大，特别是起动、制动工况。研究不同起动、制动工况下圆管带式输送机的动态特性，忽略输送带横向振动以及跑偏等带来的影响，研究输送带的纵向振动。

3.1 不同起动时间对输送带振动特性的影响

在分析不同起动时间对输送带振动特性的影响时，输送机满载起动，起动控制方式为正弦曲线，设定稳定运行速度为4 m/s，起动时间分别为10～70 s,间隔10 s，仿真时间分别为20～80 s，间隔10 s，仿真时间间隔0.01 s，对圆管带式输送机虚拟样机模型进行仿真，得不同起动时间下驱动滚筒与输送带相遇点处的张力曲线，如图2所示。

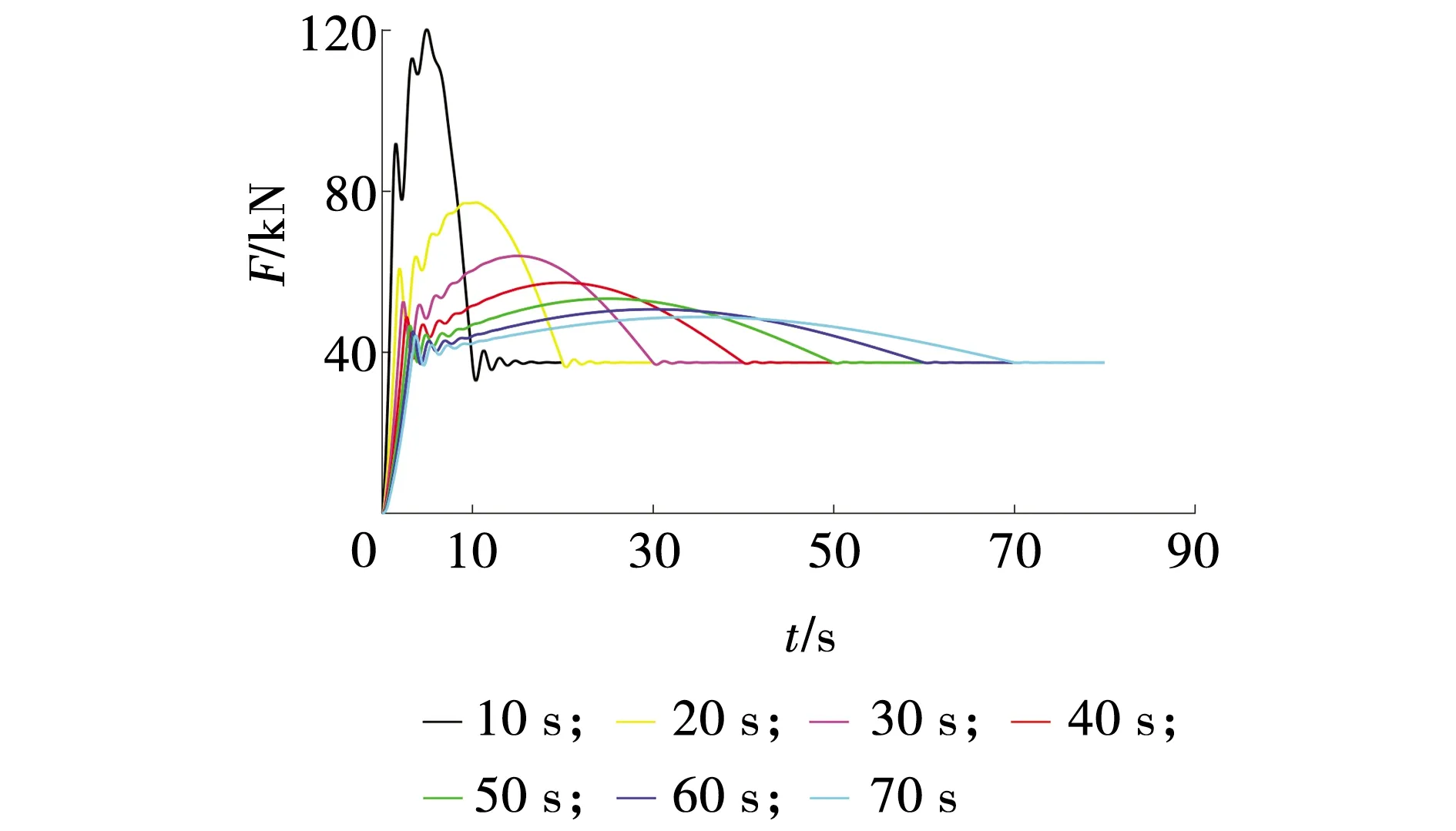
图2 不同起动时间下输送带的张力曲线Fig. 2 Tension curve of conveyor belt with different starting times

圆管带式输送机在不同起动时间下输送带张力峰值和平均张力见表1，将表1中数据点进行幂函数拟合，结果如图3所示。

不同起动时间与输送带张力峰值和平均张力幂函数拟合公式为

(4)

式中：Fm——输送带张力峰值，kN；

Fe——输送带平均张力，kN。

表1 不同起动时间输送带张力峰值和平均张力

Table 1 Peak and average belt tension underdifferent starting times

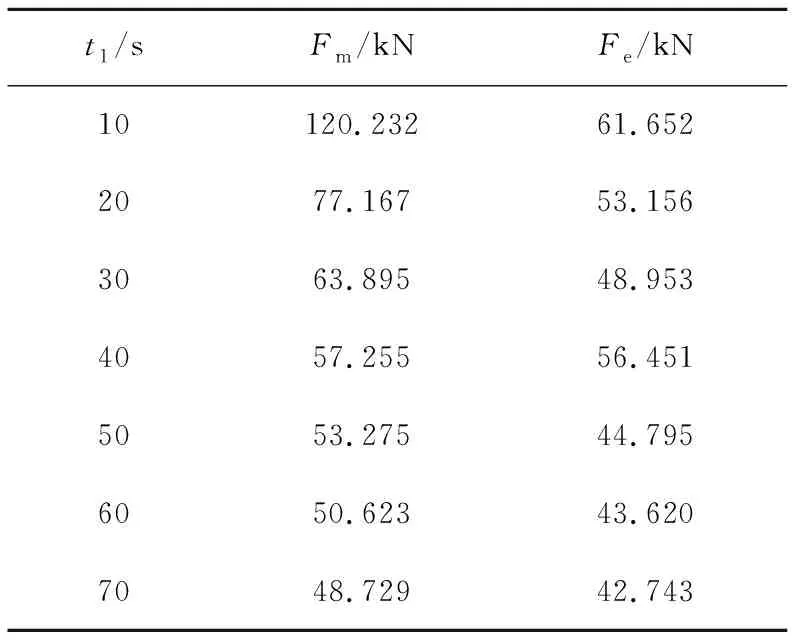
t1/sFm/kNFe/kN10120.23261.6522077.16753.1563063.89548.9534057.25556.4515053.27544.7956050.62343.6207048.72942.743

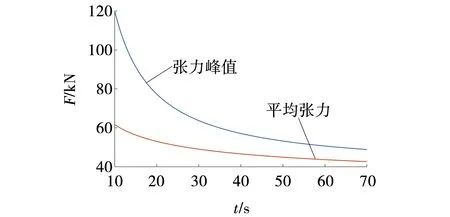
图3 不同起动时间张力峰值和平均张力 Fig. 3 Peak and average tension at different starting times

从图3可以看出，圆管带式输送机输送带头部张力峰值和平均张力随起动时间增加而降低。起动时由10 s增加至30 s，输送带张力峰值和平均张力的降幅远大于起动时间由30 s增加至70 s的降幅。由此可以得出，适当增加圆管带式输送机的起动时间可有效降低输送带的动张力，减轻输送机系统的振动，提高系统的稳定性，但也不能为降低输送带的动张力而无限地延长起动时间，过长的起动时间，对圆管带式输送机的动态特性影响不明显，反而降低了输送机的效率。

为确定圆管带式输送机最优的起动时间，确定两个优化目标，分别为起动时间t1最小，起动阶段输送带平均张力Fe最小，即优化目标为minf(t1，Fe)。输送机起动时间与起动阶段输送带平均张力量纲不同，在同时作为优化目标时，需对其进行去量纲标准化，常用的数据归一化方法为min-max标准化，其转换函数为

(5)

式中：minx——样本数据最小值；

maxx——样本数据最大值。

根据式(4)和式(5)可得优化模型为

(6)

应用Matlab对式(6)进行求解，计算结果如图4 所示。由图4可知，优化目标minf(t1,Fe)随着圆管带式输送机起动时间先减小后增大，当起动时间t1=29 s时，输送带平均张力为49.339 kN，优化目标minf(t1,Fe)最小值为0.665 5。由以上分析可知，为保证圆管带式输送机起动过程的稳定性，将起动时间设置为25～30 s较为合适。

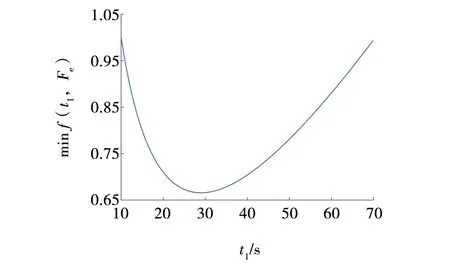
图4 起动时间优化曲线Fig. 4 Starting time optimization curve

根据2.1节编写相应的Matlab程序，以图2中不同起动时间下输送带的张力曲线为依据，求解不同起动时间下输送带张力的关联维，如图5所示。由图5可知，不同起动时间下输送带张力的关联积分双对数曲线斜率均为正值，由此可知，不同起动时间下的输送带张力的关联维均为正数，故而可判定这不同起动时间下的输送带张力均具有混沌特征。

根据2.2节编写相应的Matlab程序，以图2中不同起动时间下输送带的张力曲线为依据，求解不同起动该时间下输送带张力的K熵，如表2所示。

对表2中数据进行四次多项式拟合，得到经验公式(7)。圆管带式输送机不同起动时间下输送带张力的K熵多项式拟合曲线如图6所示。从图6可以看出，输送带张力的K熵随着起动时间的延长逐渐减小，起动时间由10 s增加至30 s，输送带张力的K熵的降幅远大于起动时间由30 s增加至70 s的降幅，由此可以得出，适当增加圆管带式输送机的起动时间可有效提高系统稳定性。

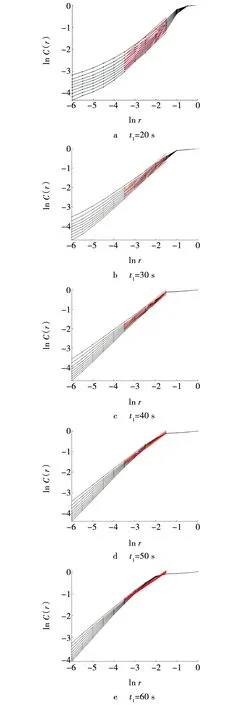
图5 不同起动时间下输送带张力的关联积分双对数曲线Fig. 5 Correlation integral double logarithm curve of belt tension under different starting time

表2 不同起动时间下输送带张力的K熵

Table 2 Kolmogorov entropy of belt tension underdifferent starting time

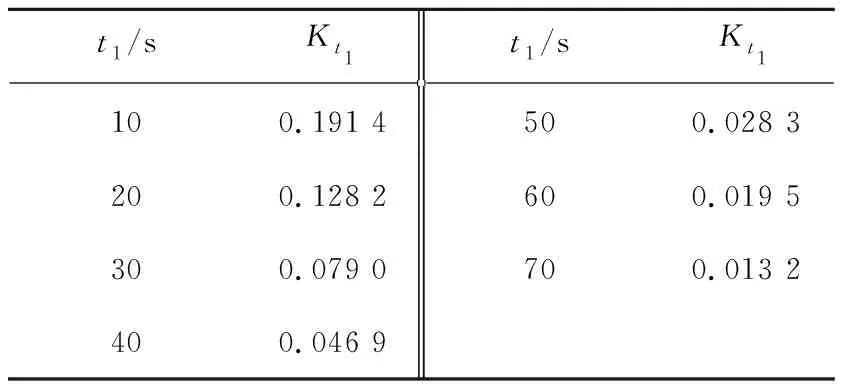
t1/sKt1t1/sKt1100.191 4500.028 3200.128 2600.019 5300.079 0700.013 2400.046 9

(7)

式中，Kt1——不同起动时间下输送带张力的K熵。

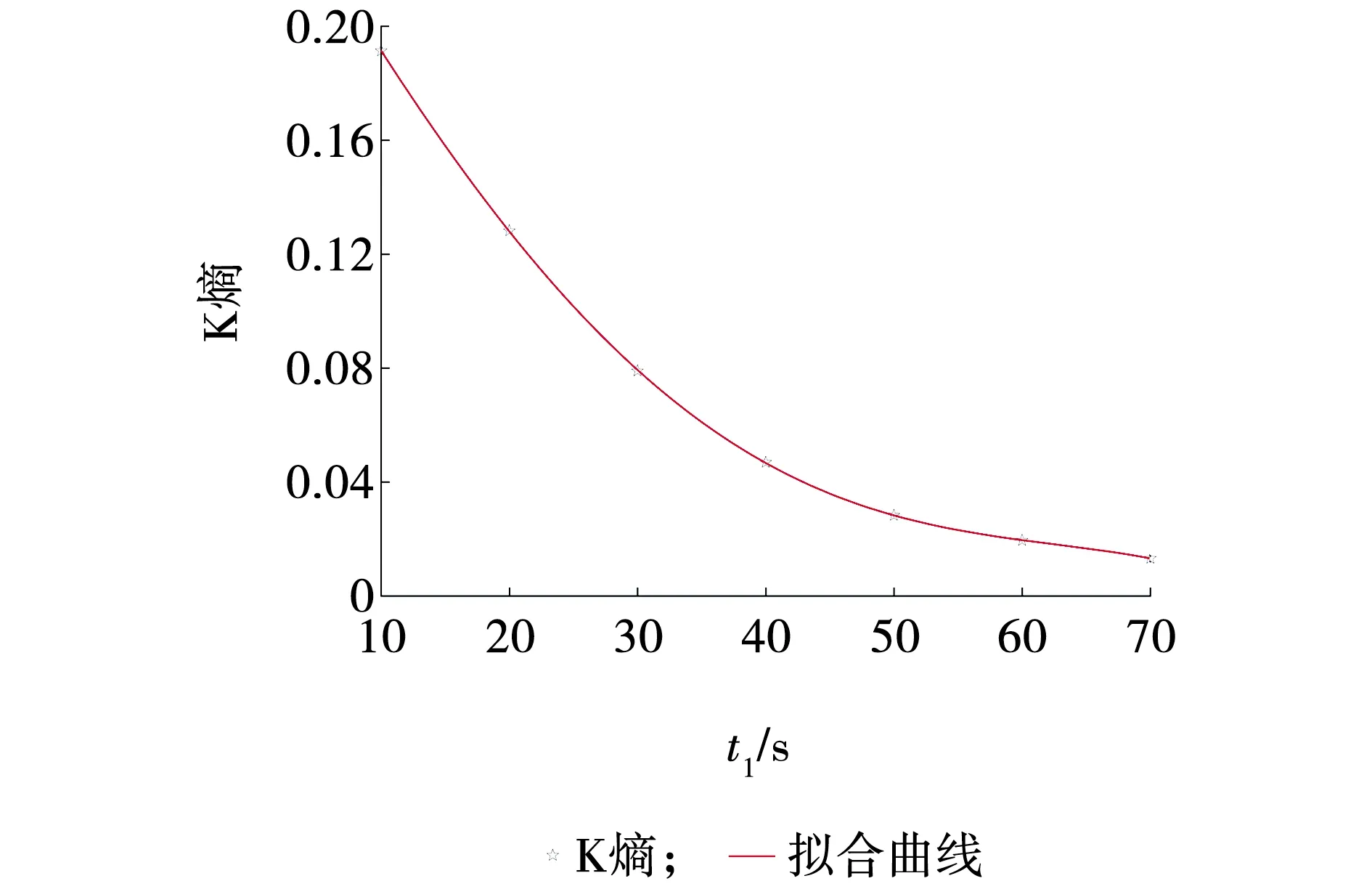
图6 不同起动时间下输送带张力的K熵拟合曲线 Fig. 6 Kolmogorov entropy fitting curve of belt tension under different starting time

3.2 不同制动时间对输送带振动特性的影响

考虑到实际工况下的制动过程，输送机在制动时为满载，在仿真中进行制动之前，需要将圆管带式输送机起动至稳定运行阶段，为比较不同制动时间与不同起动时间下的输送带张力大小，仿真过程中，起动时间设置同制动时间一致，驱动速度控制方式为反正弦曲线，设定稳定运行速度为4 m/s，制动时间分别为10～70 s，间隔10 s，稳定运行时间分别与起动制动时间相同，运行仿真模型。仿真时间分别为40～220 s，间隔30 s，仿真时间间隔0.01 s，对圆管带式输送机虚拟样机模型进行仿真，得不同制动时间下驱动滚筒与输送带相遇点处的张力曲线，如图7所示。

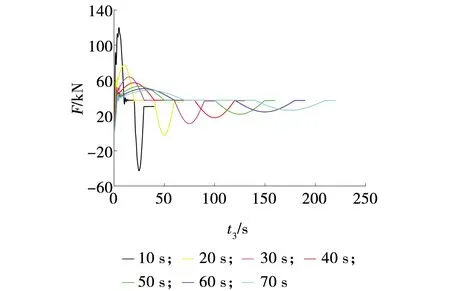
图7 不同制动时间输送带张力曲线 Fig. 7 Tension curve of conveyor belt at different braking times

由图7可见，其包含不同制动时间对应的起动以及稳定运行曲线，表3为不同起制动时间下输送带的张力，其中，起动张力峰值Fq，制动张力峰值Fz。

根据2.1节编写相应的Matlab程序，以图7中不同制动时间下输送带的张力曲线为依据，求解不同制动时间下输送带张力的关联维，如图8所示。

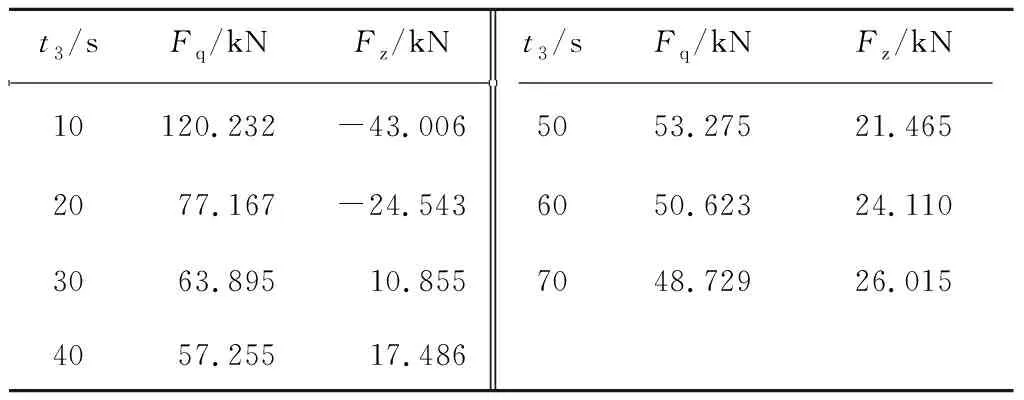
表3 不同制动时间下输送带张力

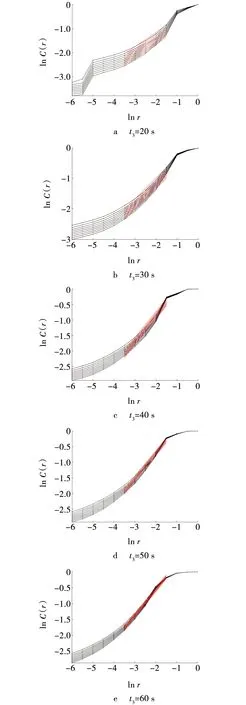
图8 不同制动时间下输送带张力的关联积分双对数曲线Fig. 8 Correlation integral double logarithm curve of belt tension under different braking times

由图7、表3可以看出，当圆管带式输送机的起动时间与制动时间相同时，输送带在制动过程中的张力峰值远小于起动过程中的张力峰值，因此可知，在圆管带式输送机起动时间与制动时间相同时，若输送机可安全起动，那么制动过程也是安全的。适当延长输送机的制动时间，可减小制动过程中输送带的动张力峰值，减轻输送机的振动，提高系统的安全性。

由图8可知，不同制动时间下输送带张力的关联积分双对数曲线斜率均为正值，由此可知，不同制动时间下的输送带张力的关联维均为正数，结合前面分析，判定不同制动时间下的输送带张力均具有混沌特征。

根据2.2节编写相应的Matlab程序，以图7中不同制动时间下输送带的张力曲线为依据，求解不同制动时间下输送带张力的K熵，如表4所示。

表4 不同制动时间下输送带张力的K熵

Table 4 Kolmogorov entropy of belt tension underdifferent braking times

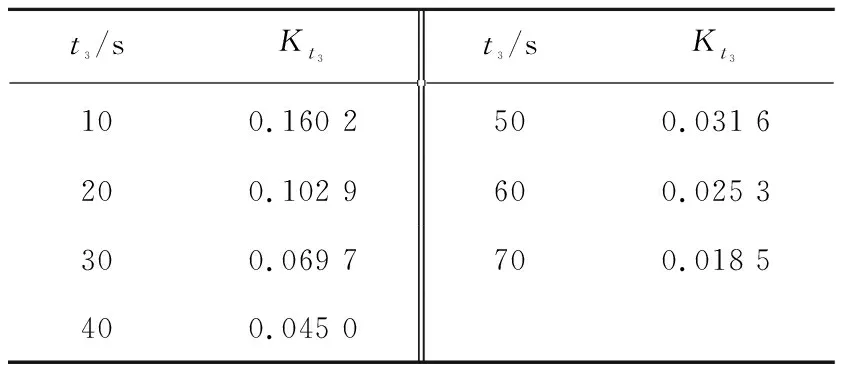
t3/sKt3t3/sKt3100.160 2500.031 6200.102 9600.025 3300.069 7700.018 5400.045 0

对表4中数据进行四次多项式拟合，得到经验公式为：

(8)

式中，Kt3——不同制动时间下输送带张力的K熵。

圆管带式输送机不同制动时间下输送带张力的K熵多项式拟合曲线如图9所示。

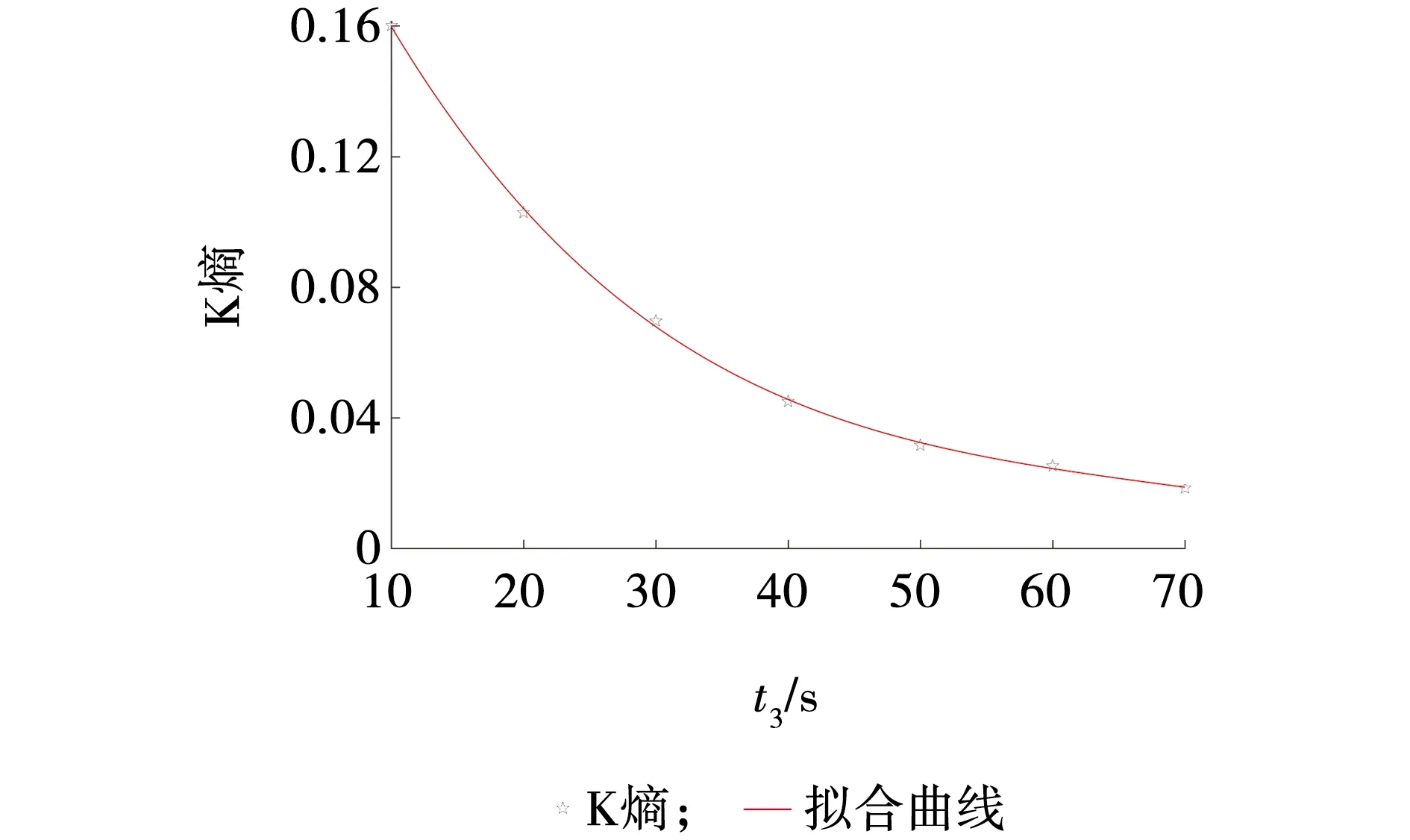
图9 不同制动时间下输送带张力的K熵拟合曲线Fig. 9 Kolmogorov entropy fitting curve of conveyor belt tension under different braking times

从图9可以看出，随着制动时间的延长，输送带张力的K熵逐渐减小，输送机系统的稳定性也越来越好，制动时间由10 s增加至30 s，输送带张力的K熵的降幅远大于制动时间由30s增加至70s的降幅，由此可以得出，适当延长制动时间可有效提高系统稳定性。

4 结 论

(1)输送机起动时间越长，输送带的张力峰值及平均值越小，输送机系统振动越小，但是过长的起动时间降低了输送机的效率，通过目标优化，为保证圆管带式输送机起动过程的稳定性，将起动时间设置为25～30 s较为合适。输送机起动时间与制动时间相同时，若输送机可安全起动，则其制动过程也是安全的。

(2)分析不同起动制动时间下输送带张力的关联维，证明输送机运行过程中输送带的张力具有混沌特征。分析不同起动制动时间下输送带张力的K熵，输送带张力的K熵随着起动制动时间的延长逐渐减小，起动制动时间由10 s增加至30 s，输送带张力的K熵的降幅远大于起动制动时间由30 s增加至70 s的降幅，由此可以得出，适当延长起动制动时间可有效提高系统稳定性。