基于丰度分布约束的NMF端元生成方法*

石悦，王宏琦，郭新毅

(1 中国科学院电子学研究所， 北京 100190； 2 中国科学院网络信息体系技术科技创新重点实验室， 北京 100190；3 中国科学院大学， 北京 100049； 4 国电联合动力技术有限公司， 北京 100039)(2018年11月12日收稿； 2019年3月18日收修改稿)

由于高光谱传感器空间分辨率的限制以及地物的复杂多样性，混合像元普遍存在于高光谱遥感图像中，因此混合像元分析受到越来越广泛的关注。线性混合模型(the linear mixture model，LMM)是国内外混合像元分解方法中应用最广泛且最简单的光谱混合模型。该模型把遥感影像的像元光谱看作是各种不同类型的纯像元(称为端元)光谱的线性组合。基于LMM的端元提取方法主要分为端元识别类方法和端元生成类方法。端元识别类方法包括纯像元指数法(pixel purity index, PPI)[1]、正交子空间投影法(orthogonal subspace projection, OSP)[2]、顶点成分分析法(vertex component analysis, VCA)[3]、高斯消元法(Gaussian elimination method,GEM)[4]、N-FINDR[5]、基于Gram行列式的快速端元提取算法(FGDA)[6]、单纯形生长算法(simplex generation algorithm, SGA)[7]和基于单形体的端元提取方法(simplex volume algorithm, SVA)[8]等。此种方法需要纯像元假设，即假设一个场景中每个端元至少有一个纯像元。端元生成类方法不需要纯像元假设，主要包括最小体积变换[9]、迭代约束端元法(iterated constrained endmember, ICE)[10]、稀疏优化ICE(sparse ICE, SPICE)[11]和几何优化模型(geometry optimization model, GOM)[12]等。

近年来，非负矩阵分解NMF(non-negative matrix factorization)的端元生成方法受到越来越多的关注。NMF端元生成方法可以同时估计出端元矩阵和丰度矩阵。Lee和Seung[13]证明NMF端元生成方法可利用乘式迭代高效快速地实现NMF目标函数的优化迭代。由于NMF目标函数是非凸的，NMF方法容易陷入局部极值[14]。为了缓解NMF方法固有的局部极值问题，通常采用增加约束来优化NMF端元生成方法。常用的优化约束包括最小体积约束(minimum volume constraint, MVC)[15]、丰度分段平滑约束[16]]、端元不相似性约束[17]、丰度稀疏约束[18-19]等。基于以上约束的NMF方法在一定程度上缓解了NMF方法的局部极值问题，但由于约束的引入，如经典MVC-NMF方法，乘式迭代规则被破坏，算法计算复杂度大幅增加。我们提出一种基于丰度分布约束的NMF方法，通过矩阵迹运算表达丰度分布离散度约束优化端元提取精度。同时可利用乘式迭代实现目标函数的迭代优化，算法计算复杂度小。

1 基于丰度分布约束的NMF端元生成方法

1.1 线性混合模型

假设线性混合模型成立，图像中每个像元向量可以表示为几个端元(纯像元)向量的线性组合，而混合系数为各个端元的丰度。线性混合模型表示如下：

(1)

(2)

0≤cij≤1.

(3)

式中：N为像素数，p为端元数，R=[r1,r2,…,rN]是大小为L×N的高光谱图像(L为波段数)。ci=[ci1,ci2,…,cip]T和cij分别为像元ri的丰度向量以及端元ej在像元ri处的丰度值。E=[e1,e2,…,ep]是L×p的端元矩阵，C=[c1,c2,…,cN]是p×N的丰度矩阵，N=[n1,n2,…,nN]是噪声矩阵。由于像元的物理意义约束，丰度满足2个约束条件：丰度和为一约束(abundance sum-to-one constraint，ASC)、丰度非负约束(abundance non-negative constraint，ANC)。

1.2 丰度分布约束

由于观测像元的物理意义约束，任意一个像元ri的丰度值ci=[ci1,ci2,…,cip]T非负，且满足sum(ci1,ci2,…,cip)=1。实际应用中，并非所有的端元都对某个混合像元有贡献，且每个端元的贡献系数也分主次，换句话说，混合像元往往是由某个端元子集混合而成，其他端元的丰度值基本接近于0。Cichocki等[20]提出的HALS盲信号分离方法也进一步印证，在丰度矩阵C分布离散程度高的情况下，可以获取较好的盲信号分离结果。

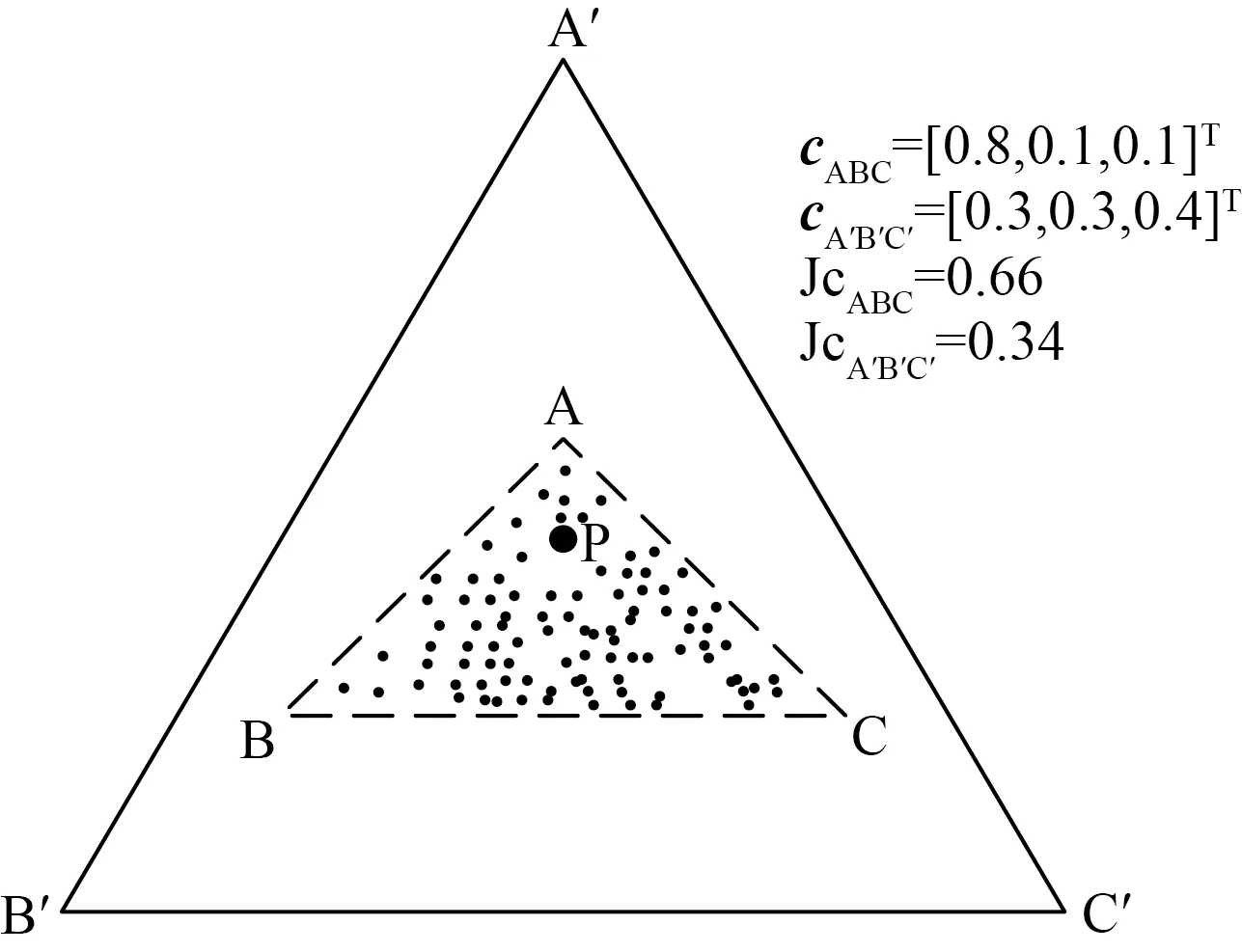
图1 丰度分布示意图Fig.1 Sketch map of abundance distribution

假设所有像元由3个端元构成，如图1所示。端元构成的单形体顶点可以是{A,B,C}，也可以是{A′,B′,C′}。在端元单形体ABC中，像元P的丰度向量cABC=[0.8,0.1,0.1]T，丰度向量cABC的距离为0.66；相应地，P在端元单形体ABC中，对应的丰度向量cA′B′C′=[0.3,0.3,0.4]T，丰度向量的距离cA′B′C′等于0.34。因此，丰度向量分布约束可由丰度向量的分布离散程度，即丰度向量的距离表示。很明显，丰度向量cABC的分布离散程度优于丰度向量cA′B′C′。因此丰度向量的分布离散程度越高，即丰度向量的距离越大，解混效果越好。

丰度分布离散度可以由丰度矩阵C的迹运算表示，即

JC(C)=trace(CTC).

(4)

因此，我们将丰度分布离散度作为一项约束应用于NMF端元生成方法。

1.3 基于丰度分布约束的NMF端元生成方法

在NMF标准方法的基础上，增加丰度分布约束，本方法形成新的目标函数：

E≥0，C≥0.

(5)

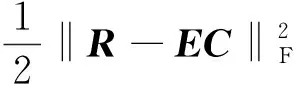
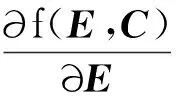
(6)

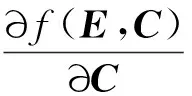
(7)

通过计算，可知

(8)

因此，

(9)

因此，目标函数的迭代优化可通过乘式迭代实现，迭代规则可以表示为：

(10)

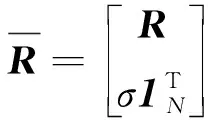
本方法可利用乘式迭代规则实现端元目标函数迭代，处理效率较高，且得到的单形体满足以下两个特点：第一是基于线性混合模型下估计和真实数据间的误差最小，类似于外力，使得端元单形体包含尽量多像元；第二是丰度矩阵离散度最高，类似于内力，使得端元单形体尽可能紧地包裹像元。

2 实验与分析

利用仿真数据和真实数据开展了一系列的实验。为验证本方法的有效性，与3种比较有代表性的方法(NFINDR-FCLS[5]、MVC-NMF[15]和NMF-ICE[21])进行比较。本方法采用NFINDR的端元提取结果作为初始值。

2.1 仿真数据

利用美国地质调查(USGS)数字光谱库中4种矿物的光谱作为端元。光谱数据共包含224个光谱波段，覆盖波长范围为0.38～2.5 μm，光谱分辨率为10 nm。仿真图像数据大小为58×58，利用Dirichlet分布生成丰度系数。为进一步去除纯像元，丰度系数均小于0.9。此外，仿真数据还添加了均值为零的白高斯噪声，以模拟可能存在的误差和传感器噪声。为了公正地评价所提出方法的有效性，在SNR=20 的情况下开展对比实验。其中NFINDR-FCLS、MVC-NMF、NMF-ICE分别依据参考文献[5,15,21]进行参数选取，本方法选择迭代次数为150次，α=0.01，σ=20。

本方法利用文献[14]中的rmsSAD(光谱角度散度)、rmsAAD(丰度角度散度)、rmsSID(频谱信息散度)、rmsAID(丰度信息散度)评估方法的性能。从图2和图3可以看出，在NFINDR端元提取结果作为初始值的条件下，本文方法具有明显优势。

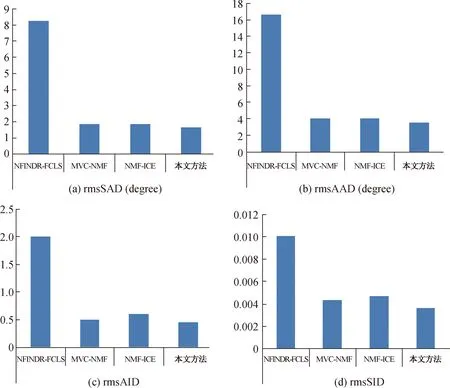
图2 误差值对比结果Fig.2 Comparison among different methods

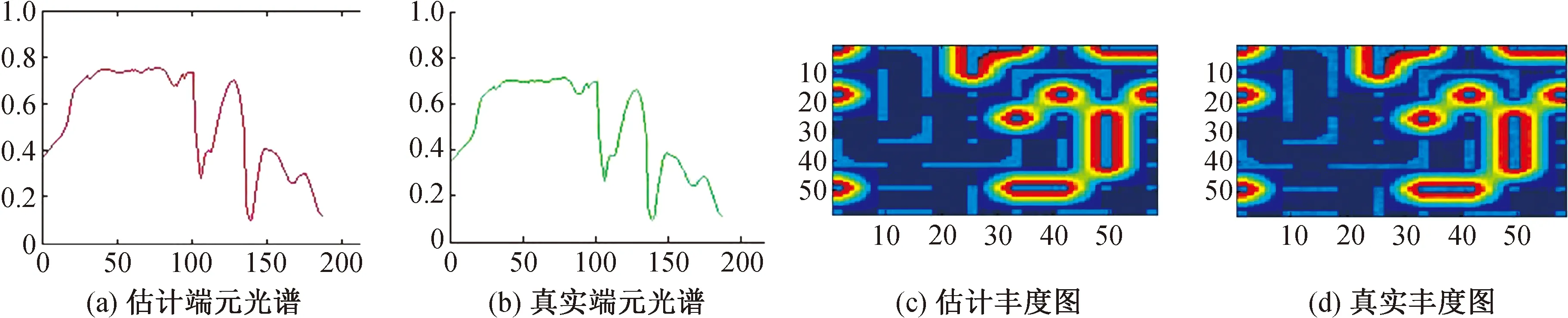
图3 本方法端元生成结果与真实端元比较Fig.3 Comparison of the extracted endmembers with real endmembers

此外, 还通过丰度RMSE分析噪声对本文方法的影响，在模拟数据中添加不同的高斯噪声(SNR=10、15、20、25、30 dB)。从图4可以看出，本文方法生成的丰度RMSE值较小，且在SNR=20 dB以后，基本不受噪声影响。

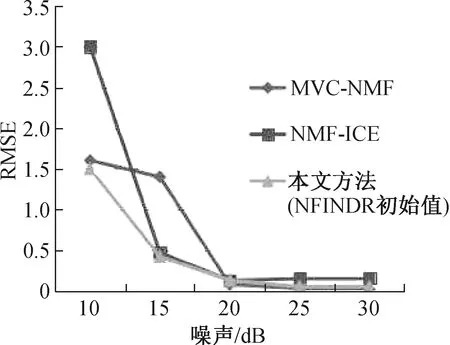
图4 不同噪声条件下丰度RMSE结果Fig.4 RMSE results of abundances at different SNR values

我们提出的端元生成方法支持利用乘式迭代进行端元优化迭代。由表1可知，在4核处理器主频2.3 GHz的条件下，本方法在图1所示的端元提取精度条件下，与其他方法相比处理时间大幅减少。

表1 模拟数据算法处理时间Table 1 Processing time for different methods with the synthetic image

同时我们也分析了本方法在不同初始值条件下的端元提取效果。从表2可以看出，由于本文方法未考虑现有方法提出的约束，需要较好的初始值才能达到较好的端元生成结果。

表2 本方法在不同初始值条件下的性能评估Table 2 Performance under different initializations

2.2 真实数据

这里使用的高光谱图像数据，为ENVI软件提供的机载可见光红外成像光谱仪(AVIRIS)赤铜矿数据集。该数据集是一个400×350图像，由1.990 8～2.479 0 μm的短波红外线(SWIR)50波段组成。该场景已被广泛用于验证端元提取算法的性能。这个图像数据在第44个波段存在一个异常像素，反射率值为0.8左右，是由于噪声破坏而造成，如图5所示。

图5 真实实验数据Fig.5 Real image data

将提取的端元与美国地质勘察(USGS)数字光谱库的对应真实光谱进行比较，提取8个端元，并利用端元rmsSAD[14]平均值和处理时间评价本文方法的处理精度和处理效率。

设定提取的端元数为8，4类方法提取出的8个端元分别与光谱库中的真实数据进行比较。从表3可以看出，与其他方法相比，本文方法rmsSAD值优于或接近其他方法。

在4核处理器主频2.3 GHz的条件下，本次实验对各方法在以上处理精度下的处理时间进行了统计分析。从表4可以看出，本文方法既能有效提取端元，且处理效率优于其他方法。

表3 不同算法处理精度Table 3 Performance evaluation for different methods

表4 真实数据算法处理时间Table 4 Processing time for different methods with the real image

3 结束语

基于约束的NMF方法缓解了NMF目标函数非凸带来的局部极值问题，往往也造成乘式迭代规则被破坏，端元生成效率降低等问题。本文提出一种基于丰度分布约束的NMF方法，首次利用矩阵迹运算表征丰度分布离散度，可利用乘式迭代实现目标函数的迭代优化，处理效率较高。通过模拟数据和真实数据从处理精度、处理时效性和噪声鲁棒性等方面进行实验分析，本文方法可提高端元估计结果的精度和算法处理效率。由于未考虑现有方法在端元方面的约束，本方法对初始值依赖较高，希望在以后的研究中进一步改进。