泥石流危险性评价模型适用性的影响机制研究

宁志杰，周爱红，2

(1.河北地质大学勘查技术与工程学院，河北 石家庄 050031；

2.河北省高校生态环境地质应用技术研发中心，河北 石家庄 050031)

0 引言

我国幅员辽阔，地形复杂，山区面积广，又处于季风气候区，降水集中，这使泥石流灾害在我国分布十分广泛。 泥石流作为山区常见的地质灾害，往往突然爆发、毫无预兆，并且会携带大量的泥沙和石块，流动迅速，能量巨大，具有强大的破坏力，严重威胁着下游居民的生命财产安全和基础设施工程。 因此进行泥石流危险性评价不仅与泥石流灾害治理密切相关，更对防灾减灾工作有重大意义。

目前，应用于泥石流危险性评价的模型有很多，如杨洋[1]利用遗传算法优化后的BP 神经网络模型对雅康高速地区的泥石流进行危险性评价；王常明[2]结合模糊c 均值聚类和支持向量机理论各自的特点建立组合模型，对北京房山区南窖沟泥石流进行危险性评价；谢涛[3]基于Arcgis平台利用地貌信息熵理论对冰川泥石流进行了危险性评价；周仲礼[4]将粗糙集和决策树理论相结合建立泥石流危险性评价模型，对绵竹市清平乡泥石流灾害的危险性进行了评价。 上述泥石流评价模型都取得了不错的应用效果，但是缺少空间变异性对泥石流危险性评价模型的影响机制研究。

泥石流系统的空间变异性反映了不同地区泥石流系统的地形地貌和气象水文等条件的差异，而模型的适用性表征的是采用危险性已知地区的泥石流样本建立的模型，预测泥石流危险性未知地区样本危险性时的适用能力。 二者看似无关，但在泥石流危险性评价的过程中却联系紧密。 当危险性已知地区与未知地区存在空间变异性时，采用已知地区的泥石流样本建立的评价模型往往难以对未知地区泥石流样本的危险性进行有效预测。 很多研究仅仅将其视为模型适用性的问题，而没有考虑模型的适用性是否受到空间变异性的影响。 因此，本文以评价指标体系相同、空间变异性显著的云南地区和黄河积石峡水库区的泥石流数据为样本，首先基于云南地区的30 组泥石流样本建立SVM 模型，分别对云南地区及黄河积石峡水库区的6 组泥石流样本的危险性进行预测，通过预测结果分析泥石流危险性评价模型的适用性是否与空间变异性有关；然后针对空间变异性如何对预测模型的适用性造成影响的问题，采用灰色关联度模型对上述两地区泥石流样本中的评价指标进行分析，研究两地区存在空间变异性时，相同评价指标灵敏度的变化对SVM 模型适用性的影响机制。 该方法为分析泥石流危险性评价模型适用性的影响机制提供了一种新思路，分析结果将为样本所属地存在空间变异性时各类泥石流危险性预测模型的建立提供重要的参考依据。

1 基本原理

1.1 SVM 模型理论

支持向量机是根据统计学理论中的VC 理论在特征空间构建最优分割超平面，使学习器在该特征空间达到全局最优水平，然后基于风险结构最小原理保证学习器在整个空间的期望以某个概率满足一定的上界的理论[5]。 其基本过程如图1，方框和圆点分别代表了两种不同类型的样本，中间的直线H 代表一个分类函数可以将两类样本完全分隔开，若不关注空间的维数时该分类函数又称为最优分类超平面。 H1、H2分别是过两类样本中离直线H 最近的点并且平行于该直线的虚线，两条平行虚线H1、H2的间隔为分类间隔m。直线H 保证经验风险最小而H1、H2是为了保证置信区间最小，因此，虚线H1、H2上距离分类函数H 最近的向量就叫做支持向量，具体的计算过程[6，7]如下。

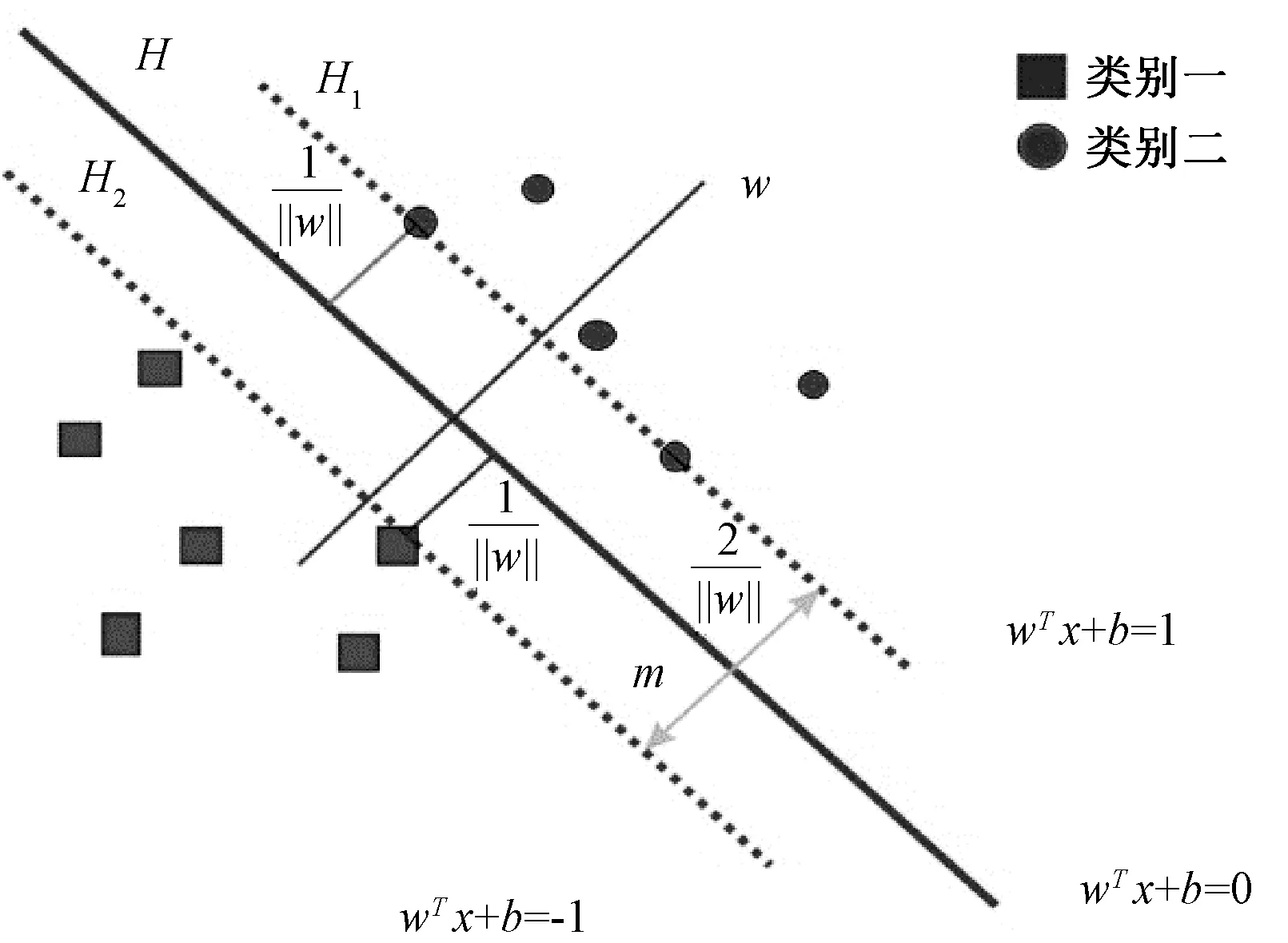
图1 最优分类超平面示意图Fig.1 Schematic diagram of optimal classification super-surface

若某训练样本包含两类不同数据{(xi，yi)，i ＝1，2，…，n}，当输入xi为第1 类数据，则输出yi＝1；当输入xi为第2 类数据，则输出yi＝- 1。 假设存在最优分类超平面H:wTx ＋b ＝0，即分类函数H 能够将两类样本准确的分配到不同侧，则xi和yi需要满足:

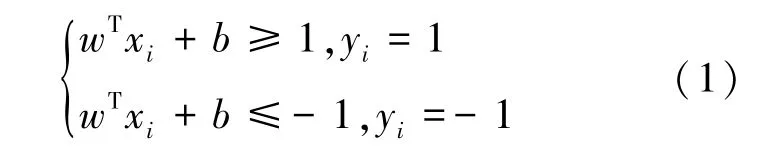
式中，w 为权值矢量；b 为偏置值。 则分类间隔为2/‖w‖，为了使H1、H2之间的距离最大化，则需满足其倒数最小化，即:

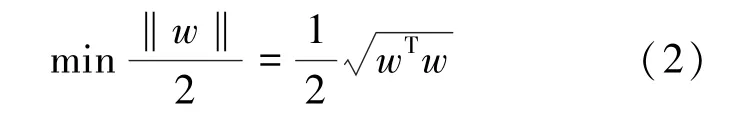
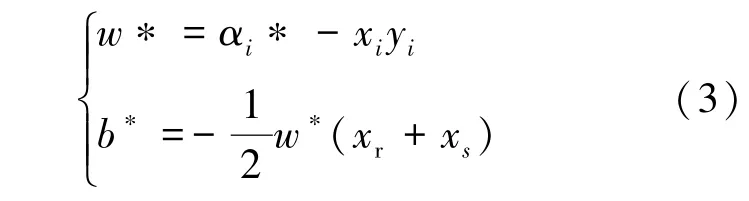
式中，αi和αj为拉格朗日乘子； C 为惩罚参数；ξi，ξi*为松弛因子；xr和xs为一对支持向量。

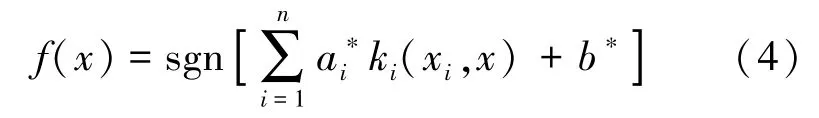
式中，ki(xi，x) 为核函数，本文中的核函数选择了应用较为广泛的径向基核函数，其公式为:

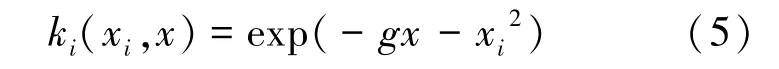
式中，g 为核宽度参数；C 和g 两个参数值通过SVM 模型对训练样本多次拟合优化获得。 本文中:xi表示泥石流样本数据中的泥石流一次最大冲出量、泥石流发生频率、流域面积、主沟长度、流域相对高差、流域切割密度、泥沙补给段长度比这7 个泥石流危险性评价的指标。 yi表示泥石流危险性等级，分为1、2、3、4 四个等级。

1.2 灰色关联度理论

中国控制论专家邓聚龙教授于1981 年提出灰色系统概念并于1982 年建立了灰色系统理论。该理论以部分信息已知、部分信息未知的灰色系统为研究对象，通过对部分已知信息的学习、开发和利用，实现对整个灰色系统的发展趋势、变化规律进行准确地反映和描述。

灰色关联度方法是灰色理论的重要研究内容，它是通过对样本中各评价指标与评价结果进行灰色关联度分析建立的一种多指标统计分析方法[8]。 灰色关联度方法的结果是得到各评价指标的权重系数，某个评价指标的权重系数越大则表明该指标与评价结果的相关程度越高，在发展过程中该指标对结果的贡献也相对较大。 采用灰色关联法确定评价指标的权重系数可以有效地避免专家打分法中主观性带来的误差，具体的计算过程为[9，10]:

(1)将泥石流样本中的危险性等级作为母因素序列，记作

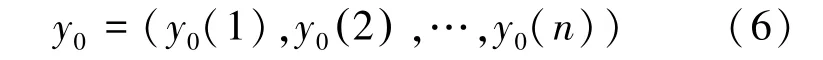
(2)将泥石流样本中与危险性有相关作用的各评价指标作为子因素序列x1，x2，…，xm，记作

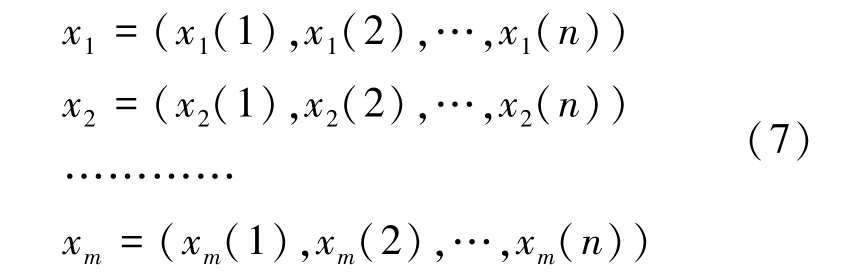
(3)记泥石流子因素序列x1，x2，…，xm对母因素危险性等级y0在评价指标k 处的关联系数为

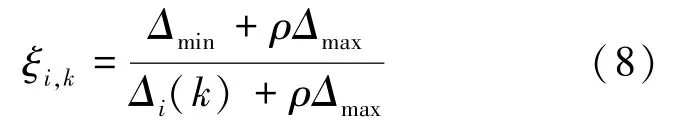
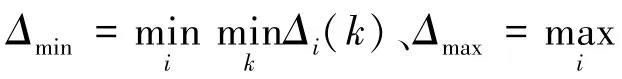
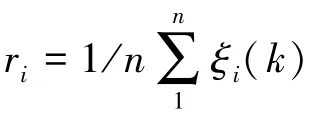
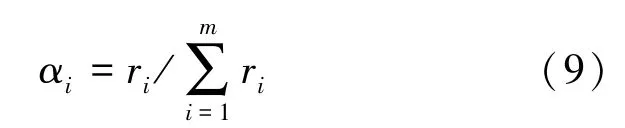
式中，αi为权重系数； ri为各评价指标相对于危险性等级的关联度；m 为评价指标的个数。

2 数据与方法

为了验证空间变异性是否对SVM 模型的适用性存在影响，本文以云南地区的泥石流样本作为训练样本建立SVM 模型，分别评价云南地区与黄河积石峡水库区预测样本的危险性。 当SVM模型对两地区预测结果的准确率相差不大时，表明空间变异性对模型的适用性影响较小；反之，表明空间变异性对模型适用性影响较大。

2.1 样本数据来源

本文以文献[11]中云南地区37 条泥石流沟中的36 条共252 个数据(危险性等级为3 级的小白泥沟中的样本数据异常，将其剔除)和文献[12]中黄河积石峡水库区的16 条泥石流沟的112 个数据为基础，并根据刘希林对泥石流评价指标的分析结果选取泥石流一次最大冲出量(S1)、泥石流发生频率(S2)、流域面积(S3)、主沟长度(S4)、流域相对高差(S5)、流域切割密度(S6)、泥沙补给段长度比(S7)作为本文的评价指标，同时根据文献[13]将泥石流划分为轻度、中度、高度、极度四个危险性等级(S0)(危险性等级由低到高分别用1，2，3，4 表示)，将其作为泥石流危险性评价的结果。

2.2 模型的建立

本文以泥石流的7 个评价指标作为输入xi，泥石流危险性等级作为输出yi。 为了保证预测样本中每个危险性等级的样本都至少有一个被包含其中，在云南地区的36 条泥石流沟中选取五郎庙河、五官屯河、花沟、黑水河、水碾河、大白泥沟等6 条沟的数据作为预测样本1(表2)，余下的30 组泥石流沟的数据作为训练样本(表1)；在黄河积石峡水库区的16 条泥石流沟中选取积东沟、阿依脑沟、瓦儿瓦斯沟、清水沟、大沟、木场沟等6条沟的数据作为预测样本2(表3)。 以MATLAB软件为依托，基于公式(1)～(5)编写MATLAB 代码，对训练样本中的泥石流数据进行处理，建立SVM 模型，当其实现对训练样本有效地识别和分类后，再利用该模型分别对预测样本1 和预测样本2 进行预测。

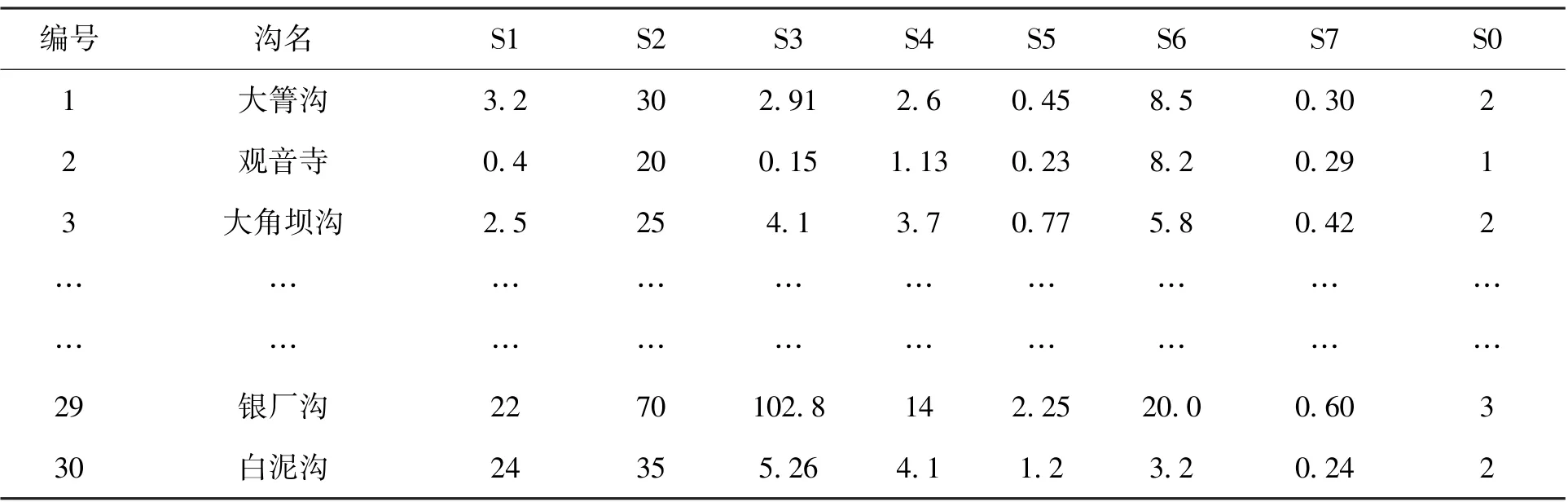
表1 云南地区30 条泥石流数据(训练样本)Tab.1 Data of 30 debris flows in Yunnan area (training samples)

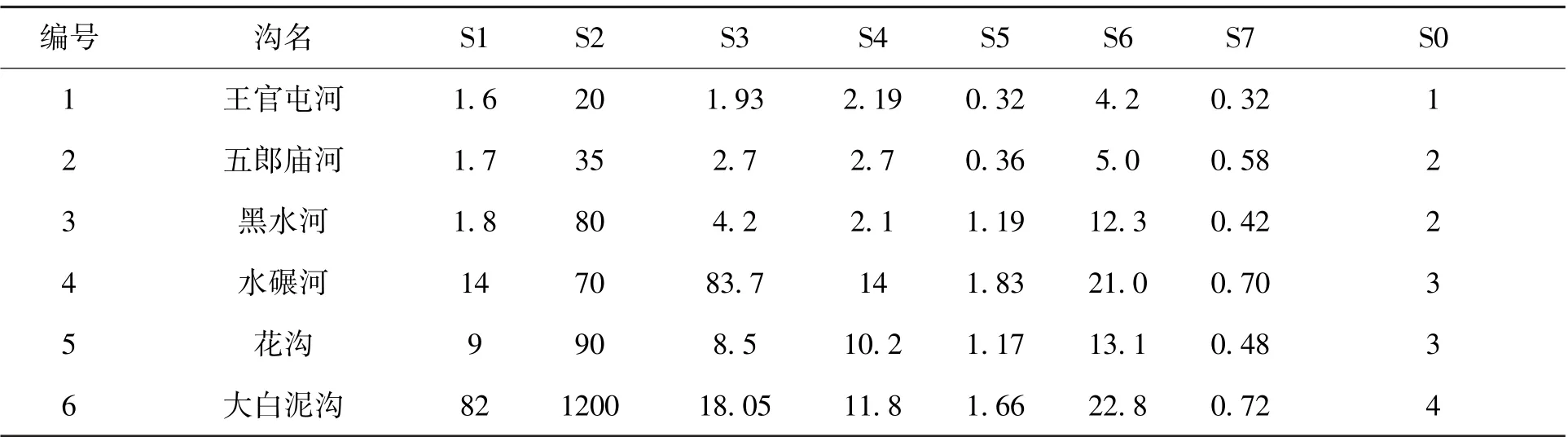
表2 云南地区的6 条泥石流数据(预测样本1)Tab.2 Data of 6 debris flows in Yunnan area (prediction sample 1)

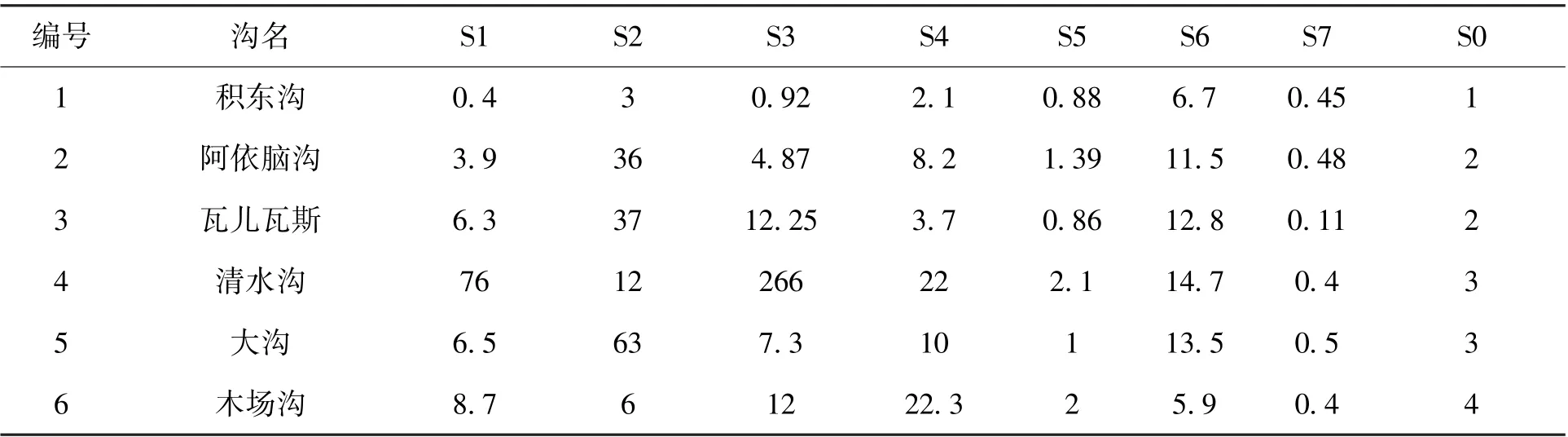
表3 黄河积石峡水库区6 条泥石流数据(预测样本2)Tab.3 Data of 6 debris flows in Jishixia reservoir area of the Yellow River (prediction sample 2)

3 SVM 模型预测结果

根据云南地区的30 组训练样本建立的SVM模型，对云南地区的6 组预测样本和黄河积石峡地区的6 组预测样本的预测结果分别如图2 和图3 所示。

由图2 可知，当采用云南地区30 组泥石流样本建立的SVM 模型对云南地区的6 组泥石流样本进行危险性评价时，只有危险性等级为4 级的大白泥沟的预测结果出现了误判，预测结果的准确率为83%，分析误判原因发现，该训练样本中只包含了2 个危险性等级为4 级的样本，可能是泥石流样本数据的不均衡性影响了SVM 模型预测效果的准确性，也就是说若排除数据不均衡性的影响，该模型能够实现对云南预测样本的精准预测。 由图3 可知，采用该SVM 模型对黄河积石峡水库区的泥石流数据进行危险性评价时准确率仅为50%，而且本次预测过程中危险性等级为3级的大沟也发生了误判，考虑到训练样本中危险性等级为3 级的泥石流样本数据较多，可以有效地排除样本数据不均衡性导致本次误判的发生。

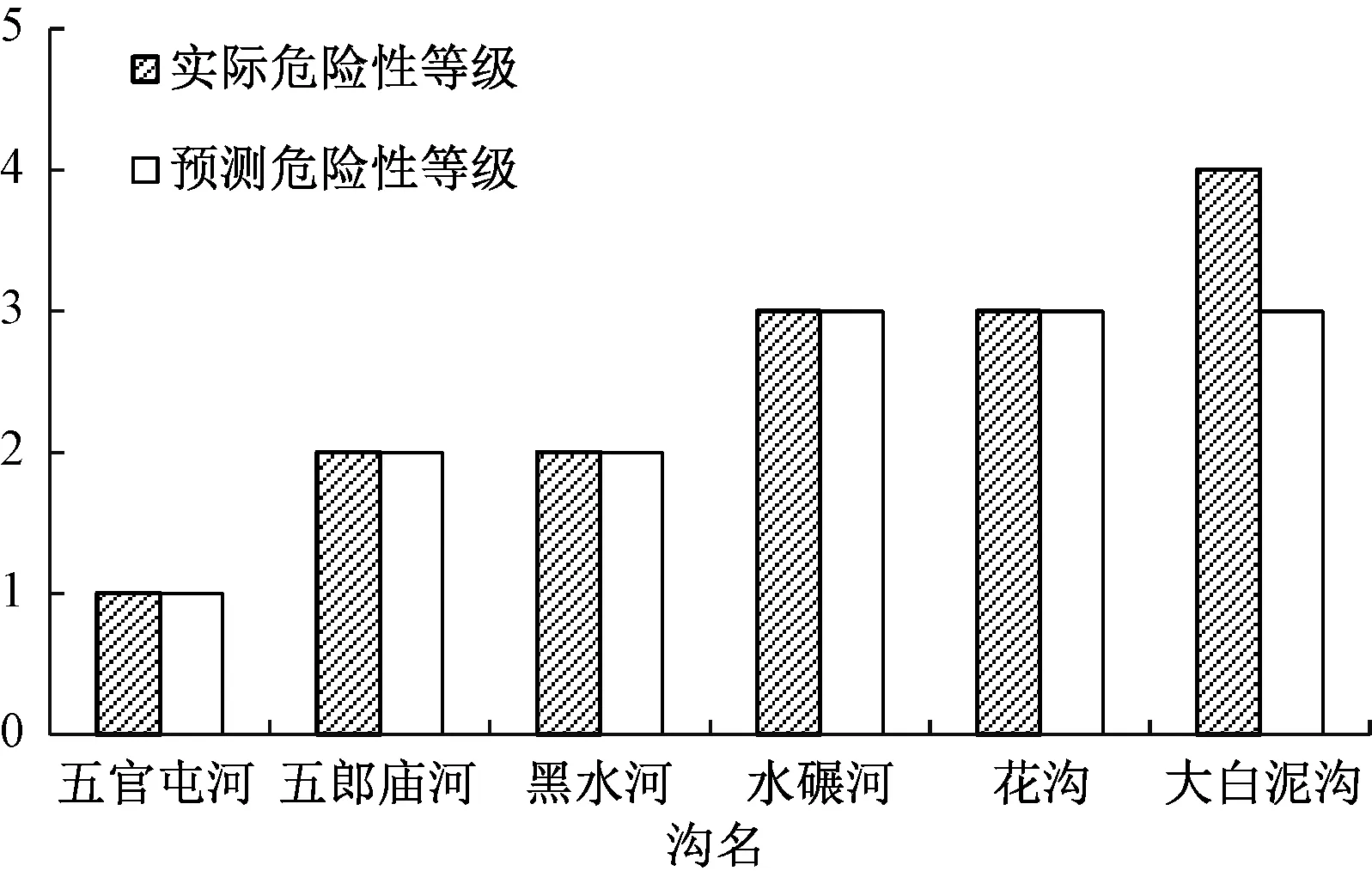
图2 云南地区6 组预测样本预测结果Fig.2 Prediction results of 6 groups of prediction samples in Yunnan area

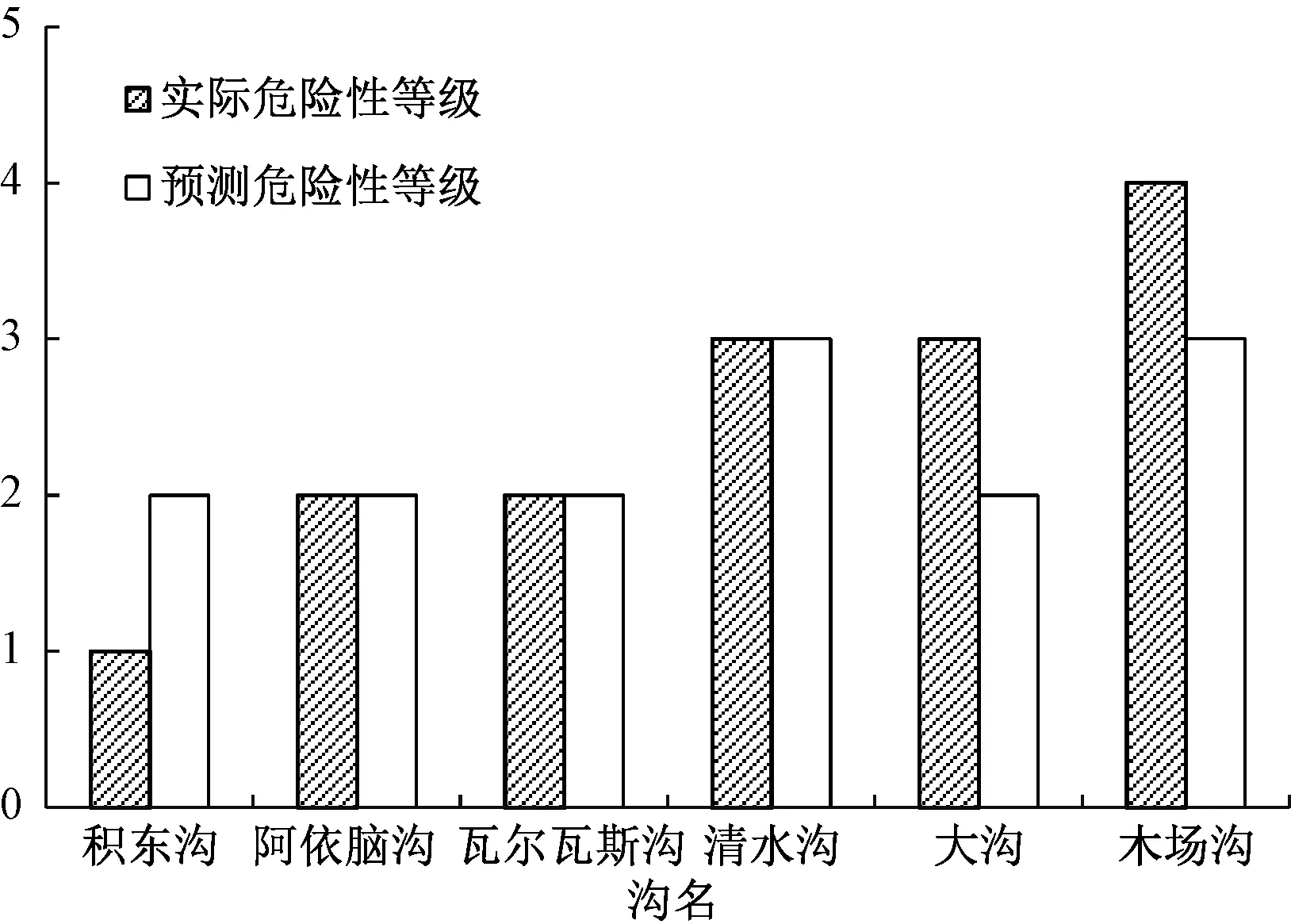
图3 黄河积石峡水库区的6 组预测样本预测结果Fig.3 Prediction results of 6 groups of prediction samples in Jishixia reservoir area of the Yellow River

由上述分析可知，模型对云南地区的预测样本实现了有效的预测，但对黄河积石峡水库区的6 组泥石流样本的危险性进行预测时，并没有展现出好的适用性。 考虑到训练样本中未包含黄河积石峡水库区的泥石流样本可能对模型的适用性有影响，因此将黄河积石峡水库区的泥石流样本添加到训练样本中重新建立泥石流危险性评价模型，但新建立的评价模型的预测精度仍未得到改善，考虑到篇幅，其过程在本文中不赘述。 通过上述分析可知SVM 模型的适用性表现出如此大的差异是由空间变异性导致的。 因此，有必要考虑泥石流系统空间变异性是如何对模型的适用性造成影响的。

4 分析与讨论

由于空间变异性对模型适用性的影响是以SVM 模型对两地区预测样本的预测效果间差异来证实的，为进一步研究空间变异性是如何影响评价模型适用性的，需要对建模过程中采用的评价指标进行分析。 因此，本文选取云南地区36 条沟的泥石流数据及黄河积石峡水库区16 条泥石流样本作为原始数据，采用式(6)以泥石流危险性等级构造母因素序列，采用式(7)以泥石流危险性评价的7 个评价指标构造子因素序列，利用式(8)和(9)进行灰色关联度分析，确定各评价指标的权重系数，权重系数越大说明该指标对泥石流危险性重要程度越高，并将两地区的评价指标按权重系数的大小进行灵敏度排序，如图4 和图5 所示。 以便探讨空间变异性影响下不同地区相同评价指标的灵敏度的变化以及评价指标灵敏度的变化对预测模型泛化能力的影响。

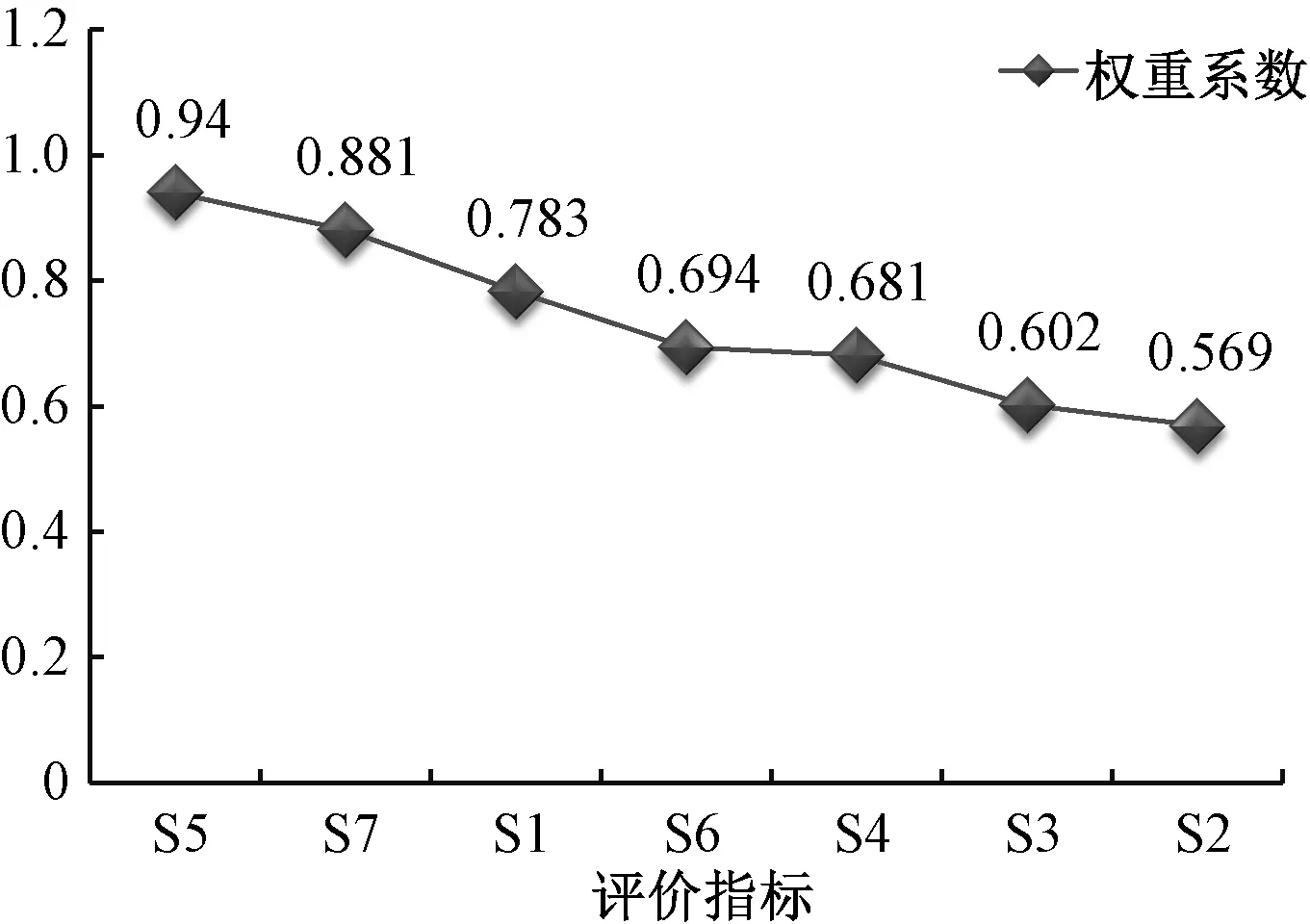
图4 云南地区评价指标灵敏度排序Fig.4 Sensitivity ranking of evaluation indexes in Yunnan area

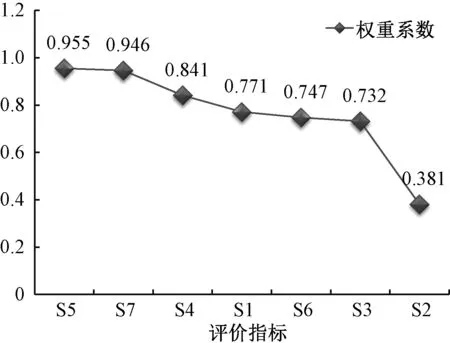
图5 黄河积石峡水库区评价指标灵敏度排序Fig.5 Sensitivity ranking of evaluation indexes in Jishixia reservoir area of the Yellow River

云南36 条泥石流沟所处位置为山原溶岩地貌，地势北高南低，多溶洞，属于低纬高原山地季风气候区，年均降雨量约1500mm，降雨多发生于5～10 月，降水量占全年的85%左右；黄河积石峡水库区16 条泥石流沟所处位置多为峡谷和沟谷平原地貌，相对切割深度较大，地形地貌条件复杂，属于半干旱高寒型气候区，年均降雨量约250mm，暴雨多发生在7、8 月份，日降水量最高可达25mm。 在两地区地形地貌和气象水文等条件如此不同的情况下，空间变异性会显著增强，因此以云南和黄河积石峡水库区泥石流样本为例，分析空间变异性影响下不同地区相同评价指标对泥石流危险性评价的灵敏度变化，来解释泥石流系统空间变异性对模型适用性的影响机制。

由图4 和图5 不难看出，云南和黄河积石峡水库区评价指标灵敏度排名前两位的均为流域相对高差(S5)和泥沙补给段长度比(S7)，表明这两个评价指标对泥石流危险性评价的重要程度应该是最大的，甚至直接控制着泥石流的危险性的划分。 但是，由于这两个评价指标在云南和黄河积石峡水库区灵敏度排序是相同的，泥石流系统的空间变异性在这两个指标中并没有得到充分的体现。

在图4 中，云南地区评价指标灵敏度排名第三、第四、第五位的分别为一次泥石流最大冲出量(S1)、流域切割密度(S6)和主沟长度(S4)，表明在采用SVM 模型预测云南地区泥石流危险性时，一次泥石流最大冲出量(S1)对预测结果的影响要大于流域切割密度(S6)与主沟长度(S4)；而在图5 中，黄河积石峡水库区评价指标灵敏度排名第三、第四、第五位的分别为主沟长度(S4)、一次泥石流最大冲出量(S1)和流域切割密度(S6)，表明在采用SVM 模型预测黄河积石峡水库区泥石流危险性时，一次泥石流最大冲出量(S1)对预测结果的影响小于主沟长度(S4)。 由上述分析可知，各评价指标在泥石流危险性评价过程中重要程度是不同的，某些指标可能相对重要，如流域相对高差(S5)和泥沙补给段长度比(S7)，某些指标在评价中重要程度相对较小，如泥石流发生频率(S2)和流域面积(S3)。 采用灰色关联度模型能够有效地对各评价指标进行灵敏度排序，并表征各评价指标的相对重要程度。

综上可知，正是因为评价指标在泥石流危险性评价的过程中重要程度不同，所以当泥石流危险性已知的地区与未知的地区间的空间变异性作用显著时(如本文中的云南地区和黄河积石峡水库区)，某些在危险性已知地区起着重要作用的评价指标(如一次泥石流最大冲出量(S1))在未知地区泥石流危险性评价中的重要程度却不如原来那么重要，极大影响了模型的适用性。 导致采用危险性等级已知地区的泥石流样本建立的危险性评价模型很难应用到泥石流危险性未知地区的危险性预测当中去。

5 结论

(1)本文基于SVM 模型在云南及黄河积石峡地区泥石流危险性评价结果，证实了泥石流危险性评价过程中泥石流系统的空间变异性是客观存在的，并且极大地影响着泥石流评价模型的适用性；基于灰色关联度模型分析空间变异性、评价指标灵敏度和泥石流危险性评价模型适用性之间的关系，揭示了在预测不同地区的泥石流危险性时，空间变异性的存在改变了评价指标的灵敏度，进而影响了SVM 模型的适用性。

(2)在泥石流危险性评价前，要对已知危险性地区的评价指标与未知危险性地区的评价指标进行分析，判断同一指标在两地区的危险性评价当中所起作用是否一致(判断是否存在空间变异性)，进而考虑是否适宜建立SVM 危险性评价模型；若已知地区与未知地区存在空间变异性，且又需要采用SVM 泥石流评价模型进行预测，建议采用主成分分析等方法提取各评价指标中包含的特征信息，这样既可以保留评价指标中的有效信息，又能够降低评价指标灵敏度的改变对模型适用性的影响。