基于元胞自动机模型的交通拥堵时间预测
2020-07-10张希仁蓝云聪
张希仁 蓝云聪

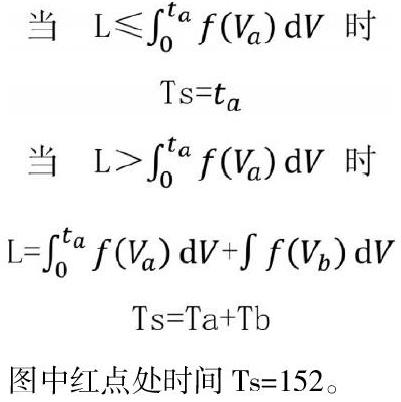
摘 要:为了更直观清楚的得出车辆实时速度和车辆通过拥挤路段所需的时间,构建SDR元胞自动机模型,对单车道、双车道、道路系统三种情况进行多次模拟,总结出三种元胞自动机模型之下拥堵时间的规律。
关键词:元胞自动机;交通;模型
一、引言
交通拥堵问题一直困扰着城市的发展,现在大数据之下能让交通拥堵情况变得事先可知,我们可以根据路况及未来路况做出选择,从而规避拥堵路段。然而我们出行不仅关心哪条道路拥堵,也关心道路拥堵 将会持续多久,在导航软件中,行程时间的估计通常是重要的功能。现有的导航软件通常通过出租车或安装了该软件的车辆来获取实时GPS数据,以确定当前的道路状况。但是交通流在时间上具有高度的随机性,动态性和复杂性,所以交通系统表出丰富的非线性特征。结果导致估计的交通拥堵时间的准确性非常差,如何去预测准确通过交通拥堵的时间是一个很有实践性意义的问题。
二、单车道元胞自动机模型
纵观所有的城市的网络系统,可将交通道路系统划分为单车道和双车道,以及由单车道和双车道组成的整个系统道路模型.
同理,我们将交通拥堵分为单车道、双车道、和系统道路模型下的拥堵,建立这三种元胞自动机模型,进行模拟可直观的得到车辆经过拥堵路段所用时间。
单车道模型,用长度为L的一维离散的格点链来表示一条单向车道,每个格点上可能有vma x+2状态:空格(表示无车),或有一辆以速度v运动的车,其中v∈{0,1,…,vma x},vma x表示车辆可以达到的最大速度.单车道元胞自动机模型在车辆更新规则中满足三方面条件:
(1)低密度时,车辆尽可能的以最大速度行驶,静止车辆的启动加速度相对运动车辆的加速度要小,可以通过GPS掌握前方车辆动态信息,从而提高车速,在安全行驶的前提下减小车间距;
(2)中密度時,车辆之间相互影响,驾驶员需要注意前车的刹车灯在前一时刻的状态;
(3)高密度时,驾驶员根据反馈信息调节车速保持安全间距行驶,避免撞车.
因为是单车道模型所以用车辆数N来衡量其密度。
下面我们引进随机慢化函数P:
其中Vn(t)和Xn(t)分别表示第n辆车在t时刻的速度和位置,dn(t)= Xn+1(t)- Xn(t)-1表示车间距,bn(t)=1(0)表示第n辆车刹车灯是开(关),P1,P2,P3是针对不同条件下的概率.定义有效间距为
其中m表示在当前车前方的第m辆车,gap取(αVn+m-1(t))四舍五入值,表示前方第 m辆车的安全间距,保证了安全行驶,前后两辆车 的安全间距与后车的速度有关,即跟驰车的车速越 大,所需的安全距离也越大.在文中m取1,2,3,分 别对应着当前车前方的第一辆车,第二辆车和第三 辆车.α定义为速度调节因子。
单车道元胞自动机模型的演化规则包括如下四个步骤:
当前车的车速Vn(t)以及两车间的车间距dn(t)决定随机慢化参数P;接下来的三步计算第n辆车在下一时刻的车速Vn(t+1)。第二步表示车辆状态在非刹车情形下将会加速行驶,直到最大限速。如果前车和当前车刹车灯关闭,该车加速行驶,并且速度可达Vmax,第三部,保证安全性,应用减速规则,再考虑有效间距根据减速度D实行减速。如果当前车速减慢,刹车灯亮,即bn+1(t)=1.下一步引入了由第一步决定的随机慢化概率P,某些车辆会进行随机慢化.刻画了由于驾驶员具有主观能动性,谨慎的司机会刹车,激进的司机则不会.最后车辆位置得到更新,并初始化刹车灯状态。
对单车道元胞自动机模型模拟。模拟上述的单车道元胞自动机模型,主要引入参数单车道上车辆数N,车辆加速度A和车辆减速度D。在模拟过程中实时图示化观察车辆的速度,和整体系统的最大速度和最小速度。采用ticks单位衡量时间。设置系统最大速度Vmax=1
进行自动机模型,同时得出图像,该图像描述可直观得出观察车辆行驶时间。我们进行多次模拟并观察图像。
我们共进行了100组不同参数设置得模拟,以上仅为N=10时对应的图像。从多次的模拟结果中我们观察,单车道元胞自动机模型模拟结果有两大类。
第一种以(N=10 A=0.001 D=0.01)情况为例,称为拥堵自消型。
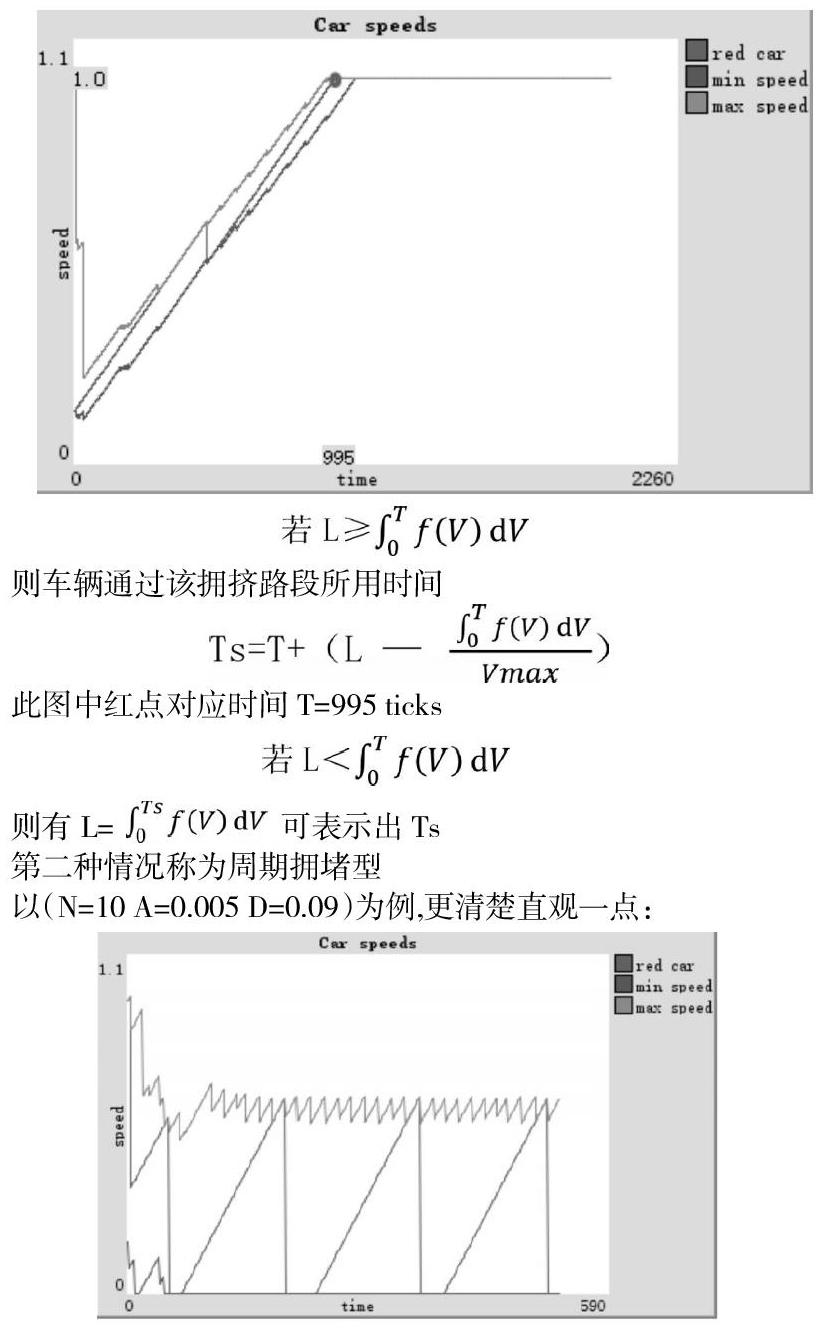
即如果L无限长,该种情况下所有车辆的速度会上升至Vmax,且此时
图中红点对应的时间即为该路段从拥挤到畅通所用时间,在(N=10 A=0.001 D=0.01 Vmax=1)情况之下。
则车辆通过该拥挤路段所用时间
此图中红点对应时间T=995 ticks
第二种情况称为周期拥堵型
以(N=10 A=0.005 D=0.09)为例,更清楚直观一点:
观察图形发现在该种情况下,如果道路无限长那么将一直循环拥堵,总时间Ts分为两部分,我们称之为过渡期Ta(绿色括号)和循环周期Tb(蓝色括号),并设过渡期函数为f(v_a ),循环周期函数为f(v_b )。
图中红点处时间Ts=152。
三、双车道元胞自动机模型
双车道元胞自动机模型以单车道模型为基础,通过GPS掌握前方车辆动态信息,在单车道规则的基础之上,多了超车换道规则,车辆是否换车道行驶的基础条件,一是此刻旁边车道有车与否,二是取决于司机的最大耐心。
因此我们在第一问的模型基础之上,引入双车道设置和司机最大耐心判断,设置两条车道0和1,及司机耐心G(1,2)。
双车道元胞自动机模型的车辆烟花规则与单车道模型也一样,分为四步(确定参数、加速、减速、位置更新)。
对双车道元胞自动机模型模拟:主要引入参数双车道总车辆数N2,车辆加速度A、车辆减速度D以及司机最大耐心G在模拟过程中实时图示化观察车辆的速度,和整体系统的最大速度和最小速度。采用ticks单位衡量时间。设置系统最大速度Vmax=1
利用自动机模型,进行多次模拟并观察图像。
通过多次模拟之后发现双车道元胞自动机模型最总所有车辆的速度都会达到稳定水平,并且若L无限大,则拥堵将一直持续。而取决于稳定速度大小的因素为司机耐心G,而其他自变量N,A,D都影响不大。观察发现,当G达到2时,系统车辆的稳定速度几乎接近于0。因此我们仅探讨了G为1或2时的情形。
所以对于双车道元胞自动机模型有:
对应Ts即为车辆经过该拥挤路段所用时间,在元胞自动机模型中,A、D、N、G都对Ts有不同程度的影响。
四、道路系统元胞自动机模拟
道路系统同样以單车道元胞自动机模型为基础,将多层单车道模型合并引入红绿灯系统,更贴合现实生活,车道上车辆演化规则保持不变,当车辆到达十字路口之后其转弯方向随机。
参数设置系统车辆数N,红绿灯循环时间Tc。道路数量M。道路系统元胞自动机模拟模拟过程如下:
同时绘制出停止车辆数、系统车辆平均速度、系统车辆平均等待时间的变化图像。同样多次进行模拟:
通过多次模拟可以看出,当道路系统道路数量和总系统车辆数一定时,三种因变量都会呈周期性结果,红绿灯循环时间Tc会正向影响其各周期的大小。而当N上调至200时,明显发现该系统发生严重的交通拥堵,并且最终全系统崩溃停止。再将M上调一个层次之后,发现崩溃的系统得到缓解。所以,道路系统元胞自动机模型中,M,Tc对交通畅通呈正相关,N对其呈负相关。
五、结果与思考
我们构建的预测车辆通过拥堵路段时间的模型,可预测车辆的实时速度和行进路程。具有很高的拟合度,实用性比较高。如果将这套模型与现在先进的GPS系统结合,利用GPS自身高精确性和实时性,结合本模型预测准确性,将大幅度减少因交通拥堵而汽车速度计算不准确而导致汽车通过拥挤路段预测不准确而带来的一系列问题。
参考文献:
[1]熊莉,陆悦,杨树芬。城市道路交通拥堵预测及持续时间研究[J]。公路,2017,62(11):125-134.
[2]严立琼,宋祖康,杨洋。 基于改进的支持向量机模型[J / OL]的交通拥堵预测。 软件指南:1-5 [2019-11-23].
