基于记忆矩阵A*引导域的VFH算法改进策略

2020-07-10庄宇辉

四川大学学报（自然科学版） 2020年4期

周俊, 庄宇辉，严华

(四川大学电子信息学院, 成都 610065)

1 引言

机器人的自主避障问题一直是一个热点研究问题. 针对此问题，目前已有许多成熟的理论，如可视图法[1]、栅格法[2]、虚拟势场法VFF(Virtual Force Field)[3]等，向量场直方图VFH(Vector Field Histogram)[4]算法亦是其中之一.

VFH算法是由密歇根大学的Johann Borenstein和Yoram Koren于1991年针对VFF算法易陷入局部最小以及震荡等问题改进而来，但该算法未考虑机器人的机械特性和运动特性，因此该团队提出了VFH+算法[5]进行改进，而后又结合启发式函数提出了VFH*算法[6]，使机器人在运动过程中更趋于目标方向.此后，有许多国内外学者在此基础上对VFH系列算法进行了改进，包括阈值敏感问题[7]、直方图构建问题[8]、动态环境问题[9]等.

但是，针对使用VFH算法避障易陷入局部死区的问题，一直没有很好的解决办法.VFH*算法提出使用启发式函数引导机器人选择方向，可在一定程度上避开死区，但随之而来的是每次方向选择时时间代价的大量增加.文献[7]提出了自适应阈值的方法，同样能在一定程度上避开死区，但也增加了时间代价.此外，以上方法能避开死区的前提是死区范围在机器人可视范围内，如果死区深度较大，机器人依然会不可避免地陷入死区.因此，本文提出了一种增加机器人“记忆”的方法，使用改进阈值策略的VFH算法的机器人在首次避障过程中将周围的环境以一个较低分辨率的矩阵存储下来.在此基础上使用A*算法[10]生成A*引导域，结合VFH算法，提出新的代价函数，使机器人在此后的避障过程中能提前避开在可视范围之外的死区，同时能够适应周围环境的动态变化.

2 算法设计

2.1 VFH 避障算法

VFH算法将求出的环境障碍物强度值以极坐标的形式转化到机器人坐标系下生成向量场直方图，该强度值与障碍物和机器人的距离成正比.选取合适的阈值，小于该阈值的障碍物强度值组成的连续区域为候选区域，在候选区域中选择合适的方向作为机器人的前进方向，在下一个位置重复以上行为，直至抵达目标点.该算法的不足之处在于阈值大小的设置直接影响候选方向的选择，当阈值较大时，机器人可选方向较多，但容易陷入死区，如图1(a)所示；当阈值较小时，机器人能提前发现死区，从而提前转向，如图1(b)所示.

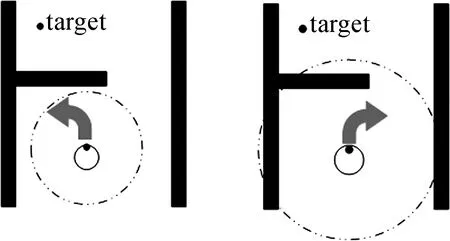
(a) (b)

Fig.1 Schematic diagram of direction selection in dead zone environment

但是，当目标点与障碍物距离较近时，若选择较小阈值，机器人无法靠近目标点，如图2所示.

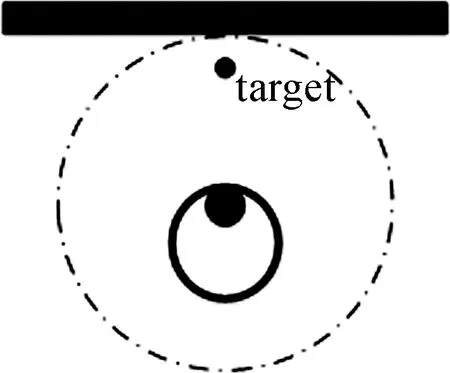
图2 目标点环境示意图

因此，采用合适的阈值选择策略对机器人的避障过程有极为重要的影响.文献[11]对阈值的选择策略进行了改进，使用动态阈值的方法，当机器人与目标点间存在障碍物时，以最小阈值获得机器人的目标航向；当机器人与目标点间不存在障碍物时，使用以最大阈值获取目标航向，在一定程度上能达到自适应的效果.但在图2目标环境下，该文献中的方法仍设置固定阈值，会因为自适应程度不够导致机器人无法到达目标点.

2.2 改进的阈值策略

结合以上分析，本文提出一种新的自适应阈值策略，根据机器人所处环境阶段的不同，分为发现目标点前和发现目标点后两种情况.

(1) 发现目标点前的策略.

① 设置机器人最小阈值Hthmin和最大阈值Hthmax.

② 以一定步长Δth对此范围内的阈值进行遍历，对应每一个阈值，使用改进的VFH代价函数计算候选方向，如下式.

(1)

其中，g(c)=μ1Δ(c,kt)+μ2Δ(c,kpre)，对应不同候选方向的代价值，Δ(c,kt)表示候选方向与目标方向的角度差，Δ(c,kpre)表示候选方向与当前前进方向的角度差.μ1,μ2需满足μ1>μ2，μ1越大，机器人选择更偏向目标方向的候选方向的可能性更高；μ2越大，机器人选择偏向目标方向的可能性更高.

由于在阈值越大的情况下，候选方向越多，更容易找到偏向目标的方向，因此计算出的g(c)值越小，若直接根据不同阈值下的g(c)值进行方向选择，机器人总会选择阈值较大情况下的前进方向.因此提出g(c)前面的自适应阈值系数项，当阈值越大时，该系数越大，h(c)越大；当阈值越小时，该系数越小，h(c)越小.以此达到在可行条件下更倾向选择较小阈值下的候选方向的目的.k∈[0,1)为安全指数，k越大，系数项的作用越明显，当k=0时，系数项成为固定值，h(c)退化为g(c).在较宽阔环境下，可选择较大的k值；在障碍物较多、较密集的环境下，可选择较小的k值.

③ 根据式(1)计算出机器人在当前位置下所有阈值及候选方向对应的代价值h(c)后，选择出h(c)值最小的方向作为前进方向.

(2) 发现目标点后的策略. 采用动态阈值Ht.根据机器人距离目标点的距离dt求出对应障碍物强度.

(2)

式中，随着dt的不断变化，Ht也将不断改变，此值作为动态阈值可使机器人顺利到达目标点.

2.3 记忆地图的生成

2.2节对VFH算法的阈值选择策略进行了改进，可以在一定程度上提前发现死区并进行规避，但若环境中死区的深度较大，在机器人的可视范围之外，那么机器人无法及时转向，仍有很大概率选择死区方向，如图3所示.

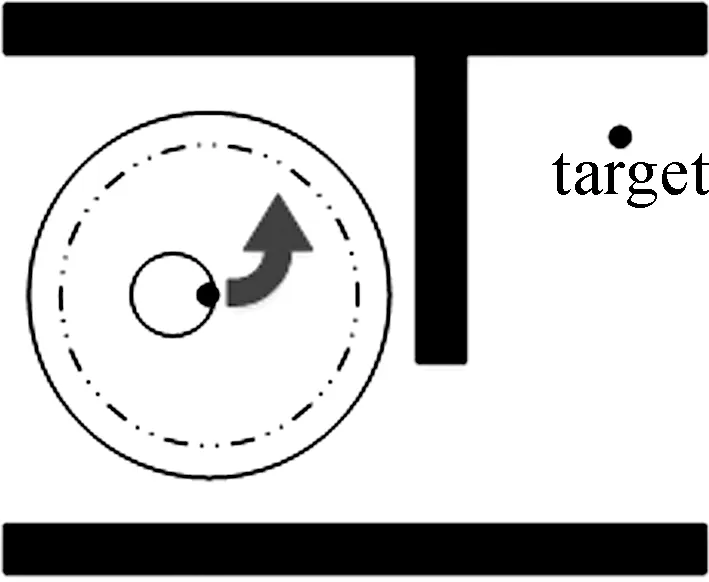
图3 机器人方向选择示意图

基于此种情况，本文将全局环境路径规划和动态避障相结合，提出“记忆矩阵”的概念，让机器人在首次避障时将周围的障碍物信息用一个较低分辨率的矩阵存储下来，在二次避障过程中提前进行全局规划，对后续避障过程起到引导作用.

(1) 障碍物点的坐标转换.机器人观察到的障碍物点(x,y)是相对于机器人坐标系的，需将其转化到世界坐标下，坐标转换图如图4所示.

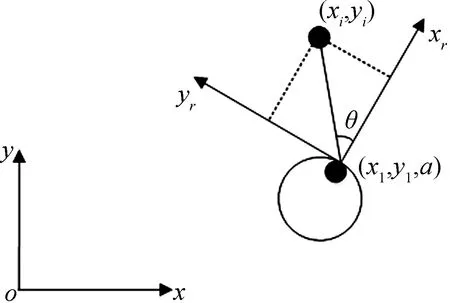
图4 坐标转换示意图

设机器人的世界坐标为(x1,y1,α)，该障碍物在机器人坐标系下的坐标为(xi,yi)，世界坐标下的坐标为

(3)

(4)

其中，xw为障碍物点在世界坐标下的横坐标；yw为障碍物坐标点在世界坐标下的纵坐标；α为当前机器人在世界坐标下的位姿角.

(2) 记忆地图的创建.对应实际的世界坐标系创建一个大小为m*n的矩阵，如图5所示.相对实际距离的缩放比例为s，将转换后的障碍物坐标点按比例缩放后存入对应的矩阵栅格中.

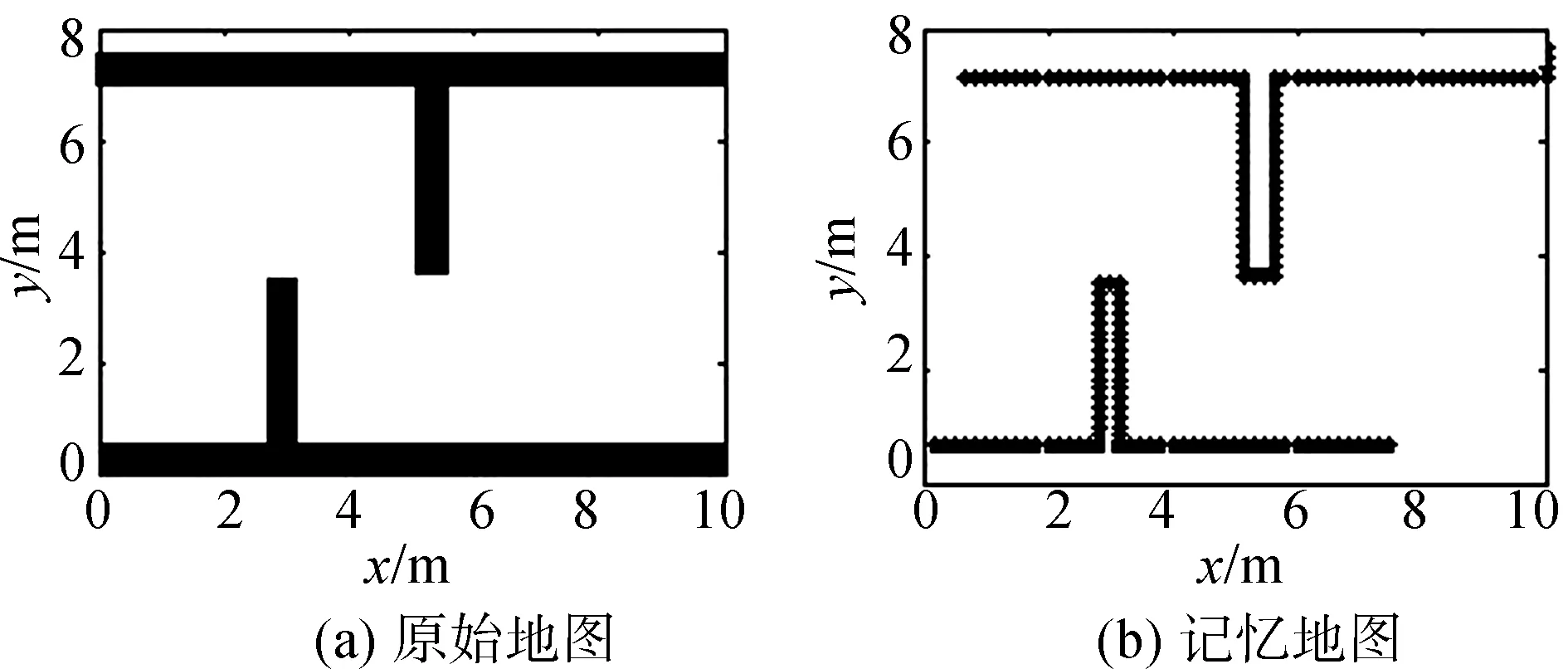
图5 记忆地图示意图Fig.5 Memory map

其中，s的大小直接影响后续全局路径规划的结果.s较小时，地图分辨率较高，规划出的路径就越精确，但耗时越长；s较大时，地图分辨率越低，规划出的路径较粗糙，但耗时越短.因此，需要选择一个合理的取值s，平衡规划路径好坏与时间的关系.

如图5(a)所示，原始地图为10 m*8 m的二维地图，对应分辨率为500*500，当s=10时，得到如图5(b)所示的记忆地图.

2.4 低分辨率A*引导域生成

根据机器人的记忆地图，以及起始点与目标点的坐标，可提前进行全局路径规划[12].在众多的路径规划算法，包括无人机航路规划[13]、智能车路径规划算法中，A*算法能保证在地图中找到最短路径，经过冗余节点去除后，生成A*引导域[14]以引导机器人的避障过程.

(1) A*寻路算法.A*算法是在Dijkstra算法的基础上发展起来的，是一种启发式搜索算法，结合了Dijkstra算法和最佳优先搜索(Best-First Search，BFS)算法的优点，用于在全局静态路径规划中寻找最短路径.A*算法通过一个代价函数来确定搜索方向，从起点开始向周围扩展，通过估价函数计算得到周围每个节点的代价值，选择最小代价节点作为下一个扩展节点，重复这一过程直到抵达目标点，生成最终路径. 其代价函数表达式为

f(n)=g(n)+h(n)

(5)

式中，f(n)是从起始点经由当前点n到目标点的移动代价估计；g(n)是起始点当前点n的实际移动代价值；h(n)是当前点n到目标点的估计代价值.

本文采用欧几里得距离度量两点之间的移动代价，如下式所示.

(6)

其中，(x1,y1)、(x2,y2)分别表示两节点的坐标.对于g(n)，(x2,y2)为当前节点时，(x1,y1)为起始节点；对于h(n)，(x2,y2)为当前节点时，(x1,y1)为目标节点.

A*算法在进行搜索时会创建一个open表和一个close表，当到达某一节点时，该节点会被添加到open表中，选择open表中代价最小的点作为下一个扩展节点，同时将该节点加入到close表中，重复该过程，直到目标节点被添加到open表中,此时close表中的路径为最终路径.

(2) 碰撞检测法去冗余. A*算法在搜索过程中是基于固定大小栅格的，最终的路径只能保证栅格相加路径最短，但可能存在大量折点，因此，本文采用碰撞检测法对路径进行去冗余处理.去冗余的思想为：对于路径中的每一个点，依次连接后面的点，进行碰撞检测，如果连接点间没有障碍物，则删除冗余节点，如图6所示.

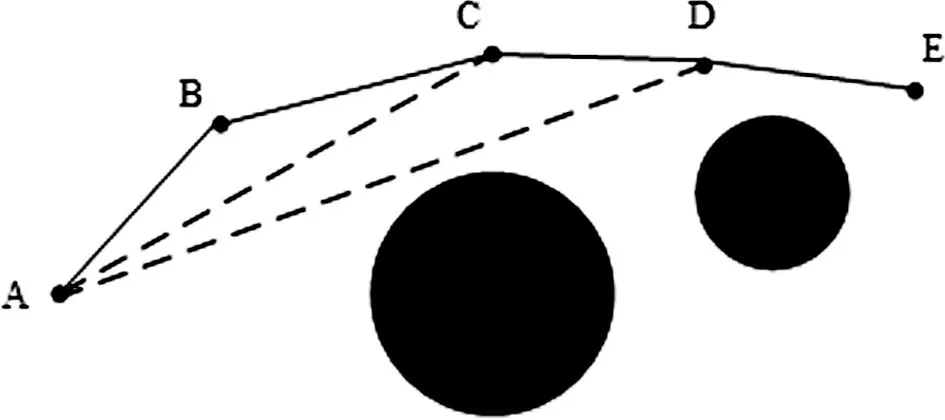
图6 去冗余节点示意图

假设路径中有A、B、C、D、E共5个节点，连接(A,C)，检测是否发生碰撞，没有则删除B节点；连接(A,D),检测是否发生碰撞，没有则删除C节点；连接(A,E),检测发生了碰撞，则开始从D节点进行搜索，直到删除所有冗余节点.

(3) 低分辨率A*引导域.A*算法对地图进行路径规划时，先将地图栅格化，栅格化大小代表了地图分辨率的不同.在起始点和目标点相同的情况下，当地图分辨率越高时，机器人规划的步数越多，相应的时间也越长；当地图分辨率越低时，机器人规划的步数越少，相应的时间也越短.针对图7所示的环境，分别进行260*200、120*100、60*50和40*35的栅格化，规划结果分别如图7中(a)、(b)、(c)和(d)所示.

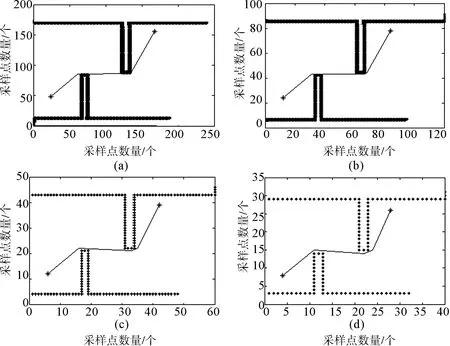
图7 不同分辨率地图下A*算法规划结果Fig.7 A* algorithm planning results

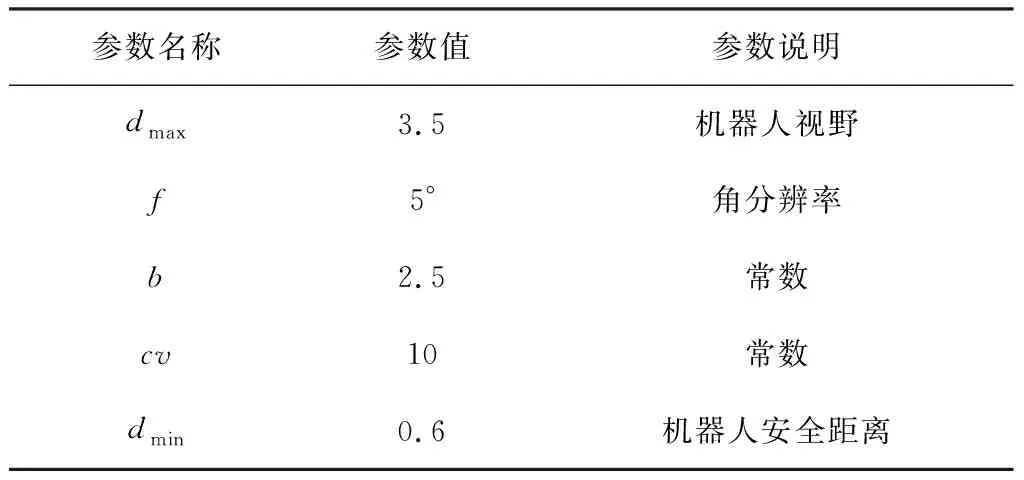
表1 不同分辨率地图下A*算法规划时间

由图7和表1中结果可知，在不同分辨率下A*算法规划路径趋势基本相似，但时间却成倍数增长.因此本文采用较低分辨率下的A*规划结果作为引导域，但前提是保证障碍物轮廓形态不变且满足以下公式.

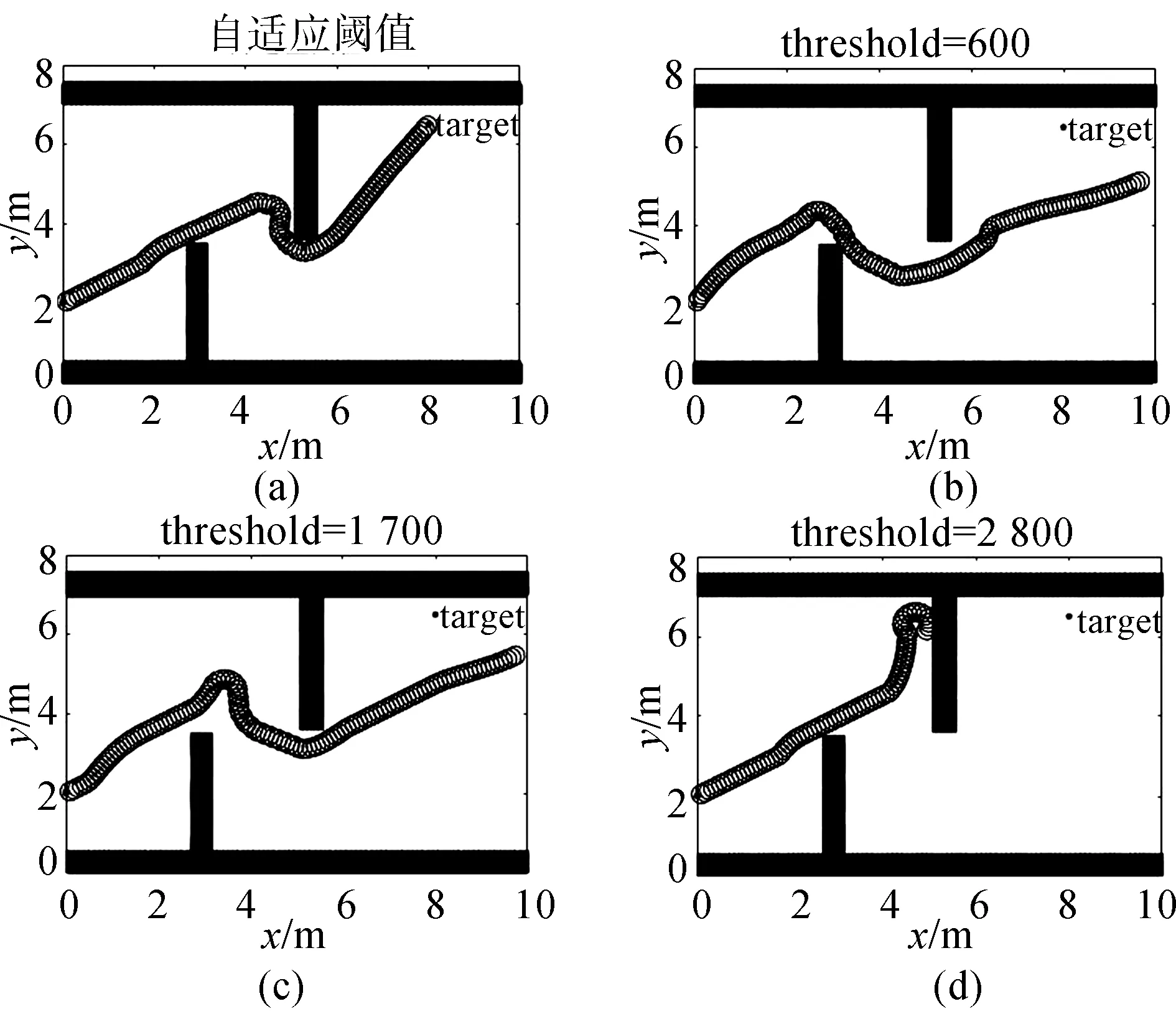
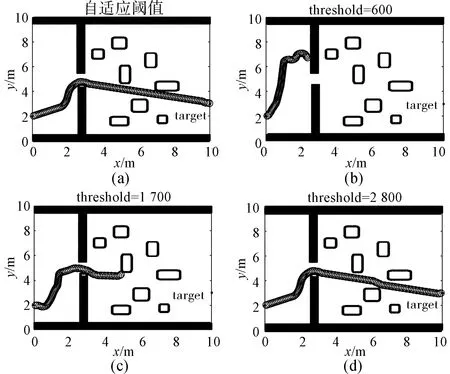
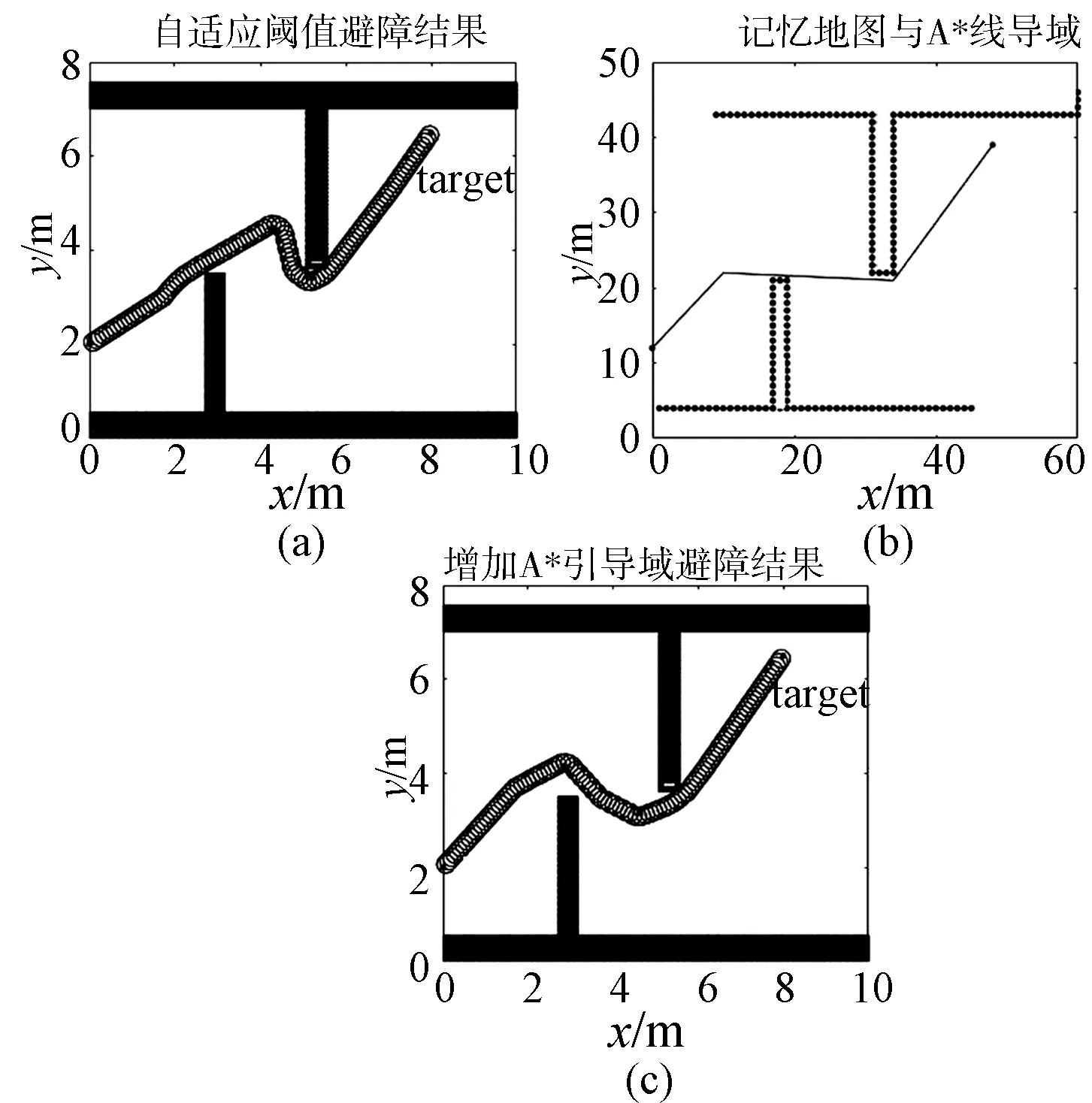
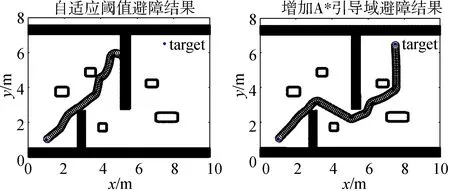
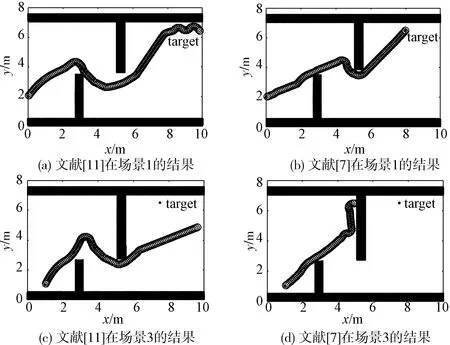
d/f

(7)

式中，d表示地图中的实际距离；f表示采样点数量，对应图像分辨率；Smin表示机器人最小可通行通道宽度. 对地图进行低分辨率处理时，其采样间距需小于机器人的最小可通行通道宽度.

2.5 机器人的方向选择

结合A*引导域和VFH算法，对机器人在每一步进行方向选择时的多个候选方向提出改进的代价函数，将A*引导域的每一个局部目标点加入到代价函数中.定义代价函数表达式为：

g(c)=μ1Δ(c,kt)+μ2Δ(c,ksub_t)+

μ3Δ(c,kpre)

(8)

式中，Δ(c,kt)为候选方向与全局目标方向的夹角；Δ(c,ksub_t)为候选方向与局部目标方向的夹角，局部目标为离机器人当前位置最近的A*引导域的目标点；Δ(c,kpre)为候选方向与机器人当前行驶方向的夹角.μ1,μ2,μ3均为常数，为保证机器人向目标点前进，需满足μ1>μ2，μ2>μ3.μ1越大，机器人选择更偏向目标方向的候选方向的可能性更高；μ2越大，机器人选择偏向局部目标方向的可能性更高；μ3越大，机器人选择与当前行驶方向最接近的方向的可能性越高.在本文的实验中，选择μ1=7，μ2=6，μ3=4.

3 实验

为验证本文所提出方法的有效性，在配置Intel(R) Core(TM) i5-3460 CPU @ 3.20 GHz处理器，4.00 GB RAM台式机中使用MATLAB R2014a进行仿真.

仿真环境是机器人容易陷入死区的10 m*10 m的不同场景二维地图，VFH算法各固定参数设置如表2所示.

表2 VFH算法参数

3.1 自适应阈值避障结果

此阶段机器人无记忆地图信息，采用自适应阈值策略进行避障.首先在一种极易陷入死区的地图环境下进行实验，自适应阈值算法各参数为：Hthmin=600，Hthmax=2800，k=0.9，Δth=1100.在场景1下实验结果如图8所示.

图8 避障结果(场景1)Fig.8 Obstacle avoidance results in scenario 1

图8是在场景1环境下采用本文提出的自适应阈值策略和采用较小阈值、中间阈值和较大阈值的实验结果对比图.可以看出，采用自适应阈值策略时，机器人会根据不同的环境综合考虑不同阈值下的方向，从中选出最好的可行方向，因此可以较好地避开死区，且能顺利抵达距离障碍物较近的目标点.采用较小固定阈值时，虽能避开死区，但由于目标点离障碍物太近，目标方向不在可通行扇区内，无法抵达终点.采用中间阈值时，机器人发现死区的时机比前者晚，因此转弯时机稍晚，且同样由于目标点离障碍物太近，目标方向不在可通行扇区内，无法抵达终点.采用较大固定阈值机器人无法提前发现进入死区，陷入徘徊，无法抵达终点.

为了验证算法的有效性，接下来在一种障碍物更多更复杂的环境下进行实验，如图9所示.

图9是在场景2环境下采用本文提出的自适应阈值策略和采用较小阈值、中间阈值和较大阈值的实验结果对比图.从实验结果可以看出，在存在狭小通道且障碍物较密集的情况下，采用自适应阈值策略可以顺利抵达目标点.采用较小固定阈值时，机器人容易忽略狭小的可行通道从而错失抵达目标点的机会.采用中间阈值进行避障时，机器人虽然经过一番徘徊找到了狭小的可行通道，但最终由于障碍物太过密集因此陷入徘徊，未能抵达终点.采用较大阈值进行避障时，机器人可以顺利抵达目标点，与自适应阈值的路径相似；这也说明了在自适应阈值策略中，机器人经过决策在此环境下自适应地选择选择了较大阈值进行避障.

图9 避障结果(场景2)Fig.9 Obstacle avoidance results in scenario 2

上述结果表明，采用本文提出的自适应阈值策略可使机器人在一定程度上避开死区，且能适应障碍物密集的区域，顺利到达目标点，自适应能力较强.

3.2 基于A*域引导的避障结果

使用自适应阈值进行首次避障产生记忆地图后，采用低分辨率A*算法的规划结果作为引导域，并在不同环境下进行实验对比.图10是机器人在场景1下增加A*引导域的前后对比结果.由图中结果可知，增加A*引导域后机器人能够更早地避开死区，提前转弯，以更优的路径到达目标点.

图10 避障结果(场景1)

为进一步验证增加A*引导域后的算法的有效性，接下来进一步增加死区深度进行实验对比，实验结果如图11所示.同时，为了验证算法适应动态环境的能力，在场景3的基础上动态增加障碍物进行实验对比，如图12所示.

图11 避障结果(场景3)

图12 动态增加障碍物后的避障结果Fig.12 Obstacle avoidance results after dynamically increasing obstacles

由图11可知，在首次避障过程中单独使用自适应阈值进行避障时，由于死区深度较大，受目标方向的影响，机器人会优先选择死区方向，然后再返回，从而出现一个较大的折点.增加A*引导域后，机器人能够根据引导域的指引，提前转弯，以更短更优的路径抵达目标点.由图12结果可知，当动态增加障碍物后不使用A*引导域进行二次避障时，由于死区深度过大和障碍物环境过于复杂，因此即使是自适应程度较高的机器人也会陷入死区；当二次避障过程中采用A*引导域后，机器人既能够避开死区，也能够动态地避开障碍物到达目标点.到达目标时的路径点数如表3所示.路径点数为“-”表示机器人未到达目标,路径点数越少表示路径越短.

表3 算法效果对比表

结合表3及上述实验结果图可知，增加A*域的引导可以使机器人到达目标点的路径更短.同时，在动态新增障碍物的环境下，使用A*域引导可使机器人提前转向避开死区，且保留了VFH算法实时动态避障的特性，最终以较短的路径到达目标.

为进一步验证算法的先进性和有效性，接下来与文献[7]与文献[11]中提出的改进算法进行对比，分别在场景1、场景3下进行实验.

图13 避障结果Fig.13 Obstacle avoidance results

由图13结果可知，文献[11]的算法策略在场景1和场景3中均能避开死区，但无法抵达目标点.这是由于该算法在目标点附近存在障碍物时仍使用固定阈值，自适应程度不够，目标点不在可行通道内，导致其无法接近目标点.文献[7]的算法策略在场景1下与本文提出的自适应阈值策略避障结果相近，但在场景3中，由于死区深度加大，该阈值策略没有及时选择避开死区的方向，使其最终陷入死区，说明该算法存在一定局限性.