基于SPSS的多元分析在山东省物流产业中的应用

张宏硕，庞凯民，徐 淼，刘 宁

（昆明理工大学 机电工程学院，云南 昆明 650500）

0 引言

专业分拣进一步加强、科技的提高以及经济全球化的快速发展，对物流产业提出了新的要求。人们对物流产业的需求逐渐增大，并给物流相关产业如仓储配送业、交通运输业以及通信行业等带来快速发展。另外，物流业是推动经济快速增长的动力之一，其增长会使国民经济稳步发展，同时降低国民经济成本，改变国民经济的增长方式，极为重要[1]。因此，物流业对于经济增长的影响及其与经济增长之间的联系已经成为现代物流领域研究的一个重要话题。本文将在运用 SPSS软件的基础上，对山东省物流产业的相关数据进行多种方法的分析，如因子分析、主成分和聚类分析，分析影响山东省物流产业发展的重要因素，并找出其制约因素，以山东省为例探讨哪些因素是限制物流发展的主要因素，以此对山东省物流现状进行综合评价，并由此提出相应的改进建议。这有利于山东省政府根据研究结论，制定出可以促进物流业发展的政策，对山东省制定有利于物流业发展的宏观政策具有一定的现实意义。

1 相关理论方法

1.1 因子分析

因子分析[2]指的是从变量群中提取共性因子的统计技术方法。其基本思想是：根据相关性大小把变量分组，使得同组内的变量之间相关性较高，不同组的变量不相关或相关性较低。每组变量代表一个基本结构——公共因子。因子分析的方法有十几种，如重心法、影像分析法，最大似然解、最小平方法、拉奥典型抽因法等，但这些方法本质上都属近似方法，基本是以相关系数矩阵为基础的。因子分析的的步骤一般包括以下几步：（1）对数据样本进行标准化处理。（2）计算样本的相关矩阵R。（3）求相关矩阵R的特征根和特征向量。（4）根据系统要求的累积贡献率确定主因子的个数。（5）计算因子载荷矩阵 A。（6）确定因子模型。（7）根据上述计算结果，对系统进行分析。

1.2 主成分分析

主成分分析[3]是将许多具有相关性的指标，重新组合使其成为一组新的无相关性的综合指标，这些综合指标就是原始指标的线性组合，用这些综合指标去代替原指标的一种统计方法。这样的目的是既可反映原有信息，又起到降维作用。其主要原理是降维，致力于使原始数据的信息损失量达到最小。主成分分析对原有指标的主要信息具有较完整的保留程度，彼此之间相互独立，抓住了主要矛盾，使问题趋于简单。同时，主成分分析中不同指标的权数由系统自动分配，主要按其指标的重要程度，由此一来就克服了人为赋权的主观因素，使得分析结果更加准确科学。假定有n个地理样本，每个样本共有p个变量描述，这样就构成了一个n×p阶的数据矩阵

其基本步骤为：（1）确定分析变量，收集数据。（2）标准化处理。（3）标准化后的数据求协方差矩阵。（4）求R的特征值、特征向量和主成分的方差贡献率。（5）提取主成分。（6）求主成分分值，计算综合分值[4]。

1.3 聚类分析

聚类分析[5]是将物理对象或抽象对象的集合进行重新分组，最终分为由相似对象组成的多个类的统计学分析方法。其原则就是通过对比样本中各事物的性质差异，将相似性质的事物归为一类，将性质不相似的事物尽量归于不同类中。其中欧式距离[6]在聚类分析中用的最为广泛。聚类的方法有很多，其主要有系统聚类法、k-均值法、模糊聚类和有序样品聚类方法等。目前最常用的方法是系统聚类法，其基本思想是先将n个样品各自算作一类，计算它们之间的距离，再将距离最近的两类合并为一个新类，计算新类与其它各类的距离，每次减少一类，以此重复，进行两个最近类的合并，直至所有的样品合并为所需类数为止。其步骤为：（1）选择“分析”—“分类”—“系统聚类”进入系统聚类设置选项卡（2）进入选项卡，将标准化后的数据作为变量，然后可以在当中选择聚类的各种方式方法及要生成的图标（3）点击确定即可看到SPSS自动处理输出的结果（4）根据SPSS输出的结果进行分析。

2 数据获取及模型求解

2.1 数据来源和指标选取

本文以山东省为例，以 2017 年中国统计局所公布的数据，选取中国统计年鉴[7]中2016 年“地区生产总值”、“人均生产总值”以及“社会消费品零售额”作为影响物流需求规模的指标；选取“公路里程以及民用汽车拥有量”作为影响物流供给的指标；选取“第一产业产值”、“第二产业产值”和“第三产业产值”作为影响产业结构的指标。具体选择的指标如下所示：

其中，三大产业产值考虑了经济结构对物流业规模的需求以及区域经济总量的影响。原始数据见表1所示。本文运用SPSS中的数据分析方法，对表1中数据进行处理分析，得出结论。

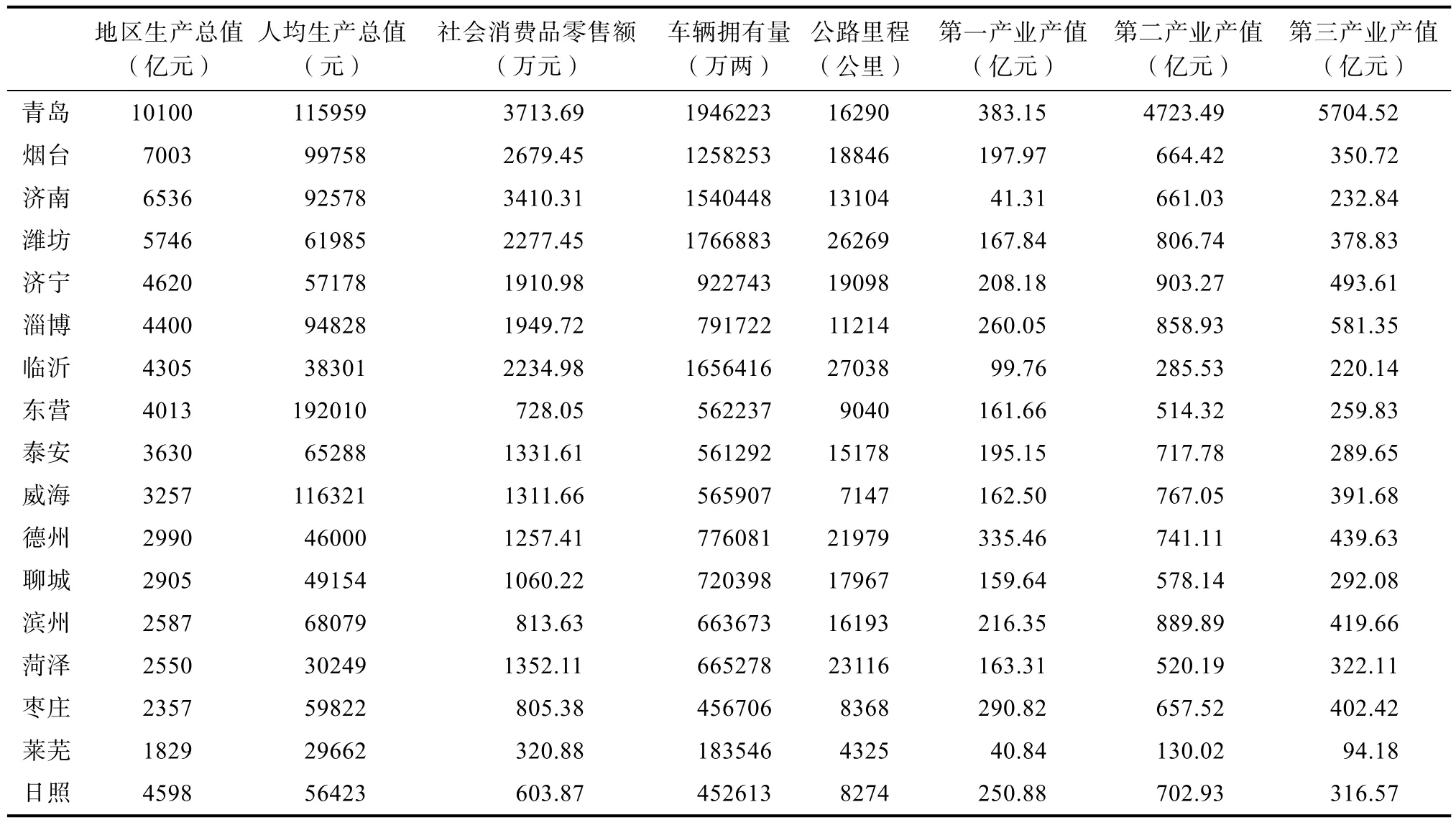
表1 山东省各地区8项主要指标情况统计Tab.1 Statistics of eight main indexes in shandong province

2.2 聚类分析

使用系统聚类方法分析数据，为了使不同量纲、不同数量级数据相互之间可以比较，首先对数据进行标准化处理[8]；其次求出经过标准化处理之后17地市数据的欧氏距离；假定17个城市作为17个类别，用类间距离法[9]定义每两个城市之间的距离；将距离最近的类进行合并，然后重新计算距离，由此进行合并以此逐渐减少类的分法。经过 SPSS处理的结果如图1、图2所示。

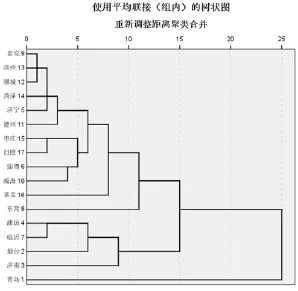
图1 17个城市的树状聚类图（组内联接）Fig.1 Tree cluster chart of 17 cities(intra-group connection)

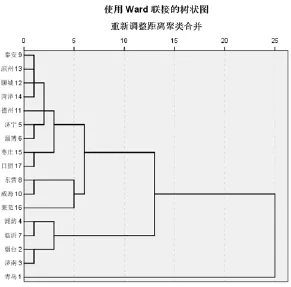
图2 17个城市的树状聚类图（Ward法）Fig.2 Tree cluster chart of 17 cities (Ward method)

本文运用系统聚类中的组内联接法和 Ward法进行对比，对比结果大体一致。从上图可看出， 17个城市被分做3大类：第一类包括（1），第二类包括（2，4，7，3），第三类包括（8，9，10，5，13，12，14，11，6，15，17，16）。1 代表的青岛，作为全国首批沿海开放城市，国务院批准的山东半岛蓝色经济区规划核心区域龙头城市，其在各个方面的优势明显，物流发展情况高于其他城市；而9，13，12，14，11，5，6，15，17，8，10，16 代表的泰安、滨州、聊城、菏泽、济宁、德州、枣庄、日照、东营、威海、莱芜，这类城市在物流发展的通讯、经济、交通条件等方面水平类似，物流发展比较落后；4，7，2，3代表的潍坊、临沂、烟台、济南，这些城市物流水平虽次于青岛，但因其经济发展水平较高，物流发展有较大潜力。

2.3 主成分分析

本文对原始数据进行标准化[10]处理，从标准化数据出发，应用统计软件SPSS24.0，以因子分析的结果进行主成分分析。

（1）求相关系数矩阵的特征值和方差贡献率[11]，并选取主成分个数，对标准化后的变量提取主成分Zi。按照方差贡献率大于 85%的原则，提取前三个主成分进行综合评价，见表2。

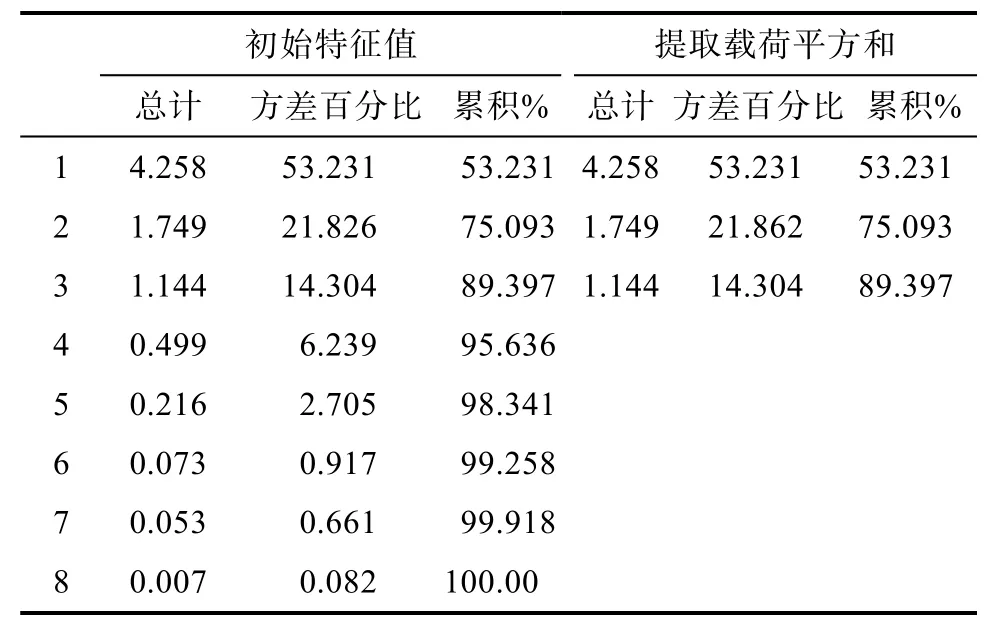
表2 总方差解释Tab.2 Total variance interpretation

（2）提取主成分。如表2所示，提取前3个特征值的主成分，前三个主成分的累计方差贡献率已达到89.397%，大于85%，表明提取的这3个主成分已经可以基本反映8个指标的所有信息，可以在一定程度上说明山东省物流产业发展的综合指标。由图3的碎石图可知，第一个主成分的特征值最高，第三个主成分之后的特征根趋势变缓，且取值很小，都小于 1，说明它们对解释原有变量的贡献很小。因此选取前三个主成分较为合适。

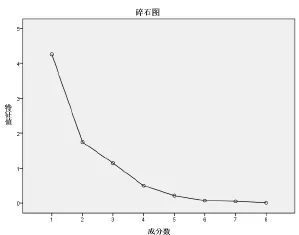
图3 主成分特征值的碎石图Fig.3 Macadam diagram of principal component characteristic values

（3）求主成分的成分矩阵，确定每个主成分所表示的含义，见表3。

表3 成分矩阵Tab.3 Component matrix

由于x2是由第几主成分解释难以确定，因此为了对因子更好地进行解释，需对因子进行旋转。

由表4可得出：各主成分的贡献率虽与旋转前的有略微变化，但三个主成分的累积贡献率一致，都是89.397%。

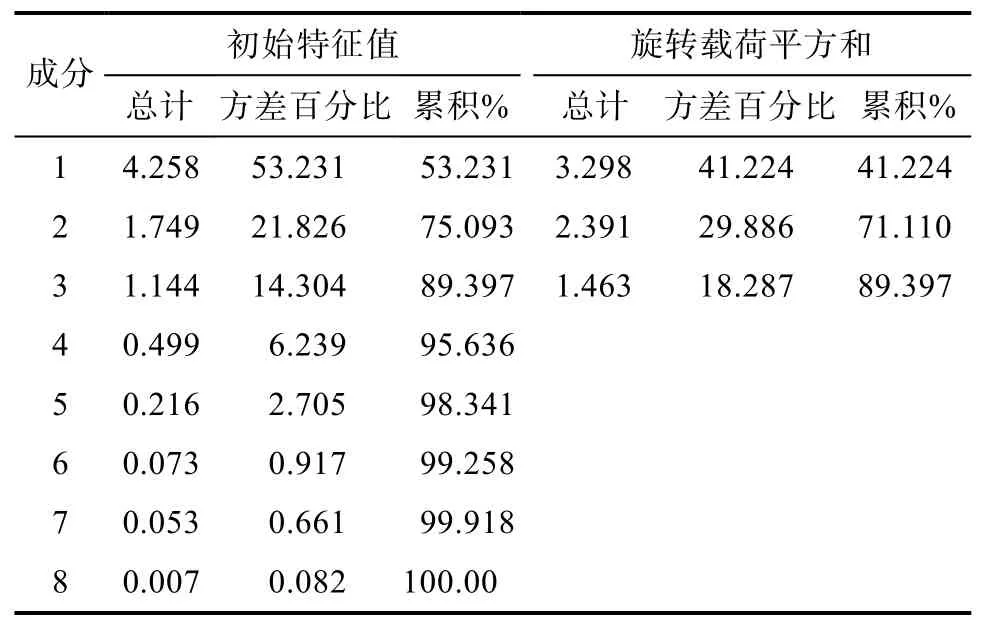
表4 旋转后总方差解释Tab.4 Interpretation of the total variance after rotation

由表5数据可以得出：1x，3x，4x，5x，主要由第一主成分解释，可以解释为第一主成分反映了物流情况中区域GDP、社会消费零售额以及物流供给产生的效果。6x，7x，8x主要由第二主成分解释，可以解释为物流情况中产业结构的影响效果。2x主要由第三主成分解释，可以解释为物流情况中人均生产总值的影响效果。

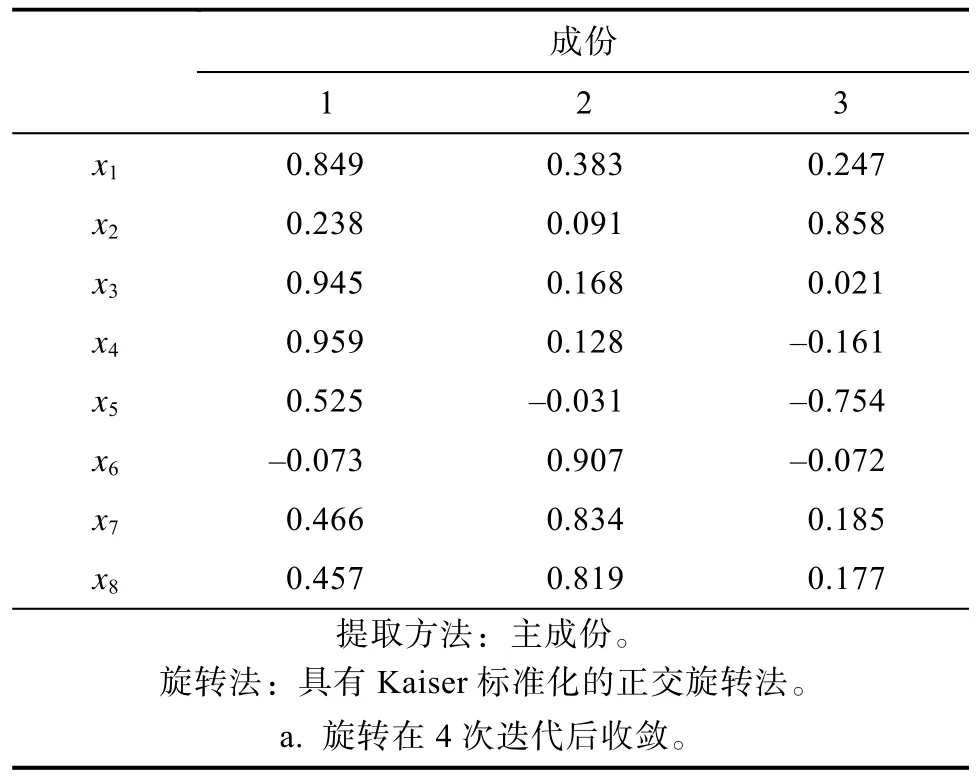
表5 旋转后的成分矩阵Tab.5 The rotated composition matrix

（4）求主成分得分系数矩阵和主成分表达式，并计算各个主成分得分和综合主成分得分。如表 6所示。

由此可得，三个主成分的线性方程如下：

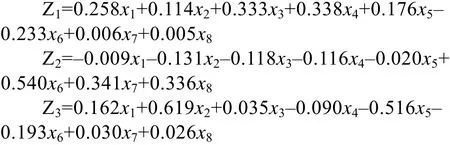
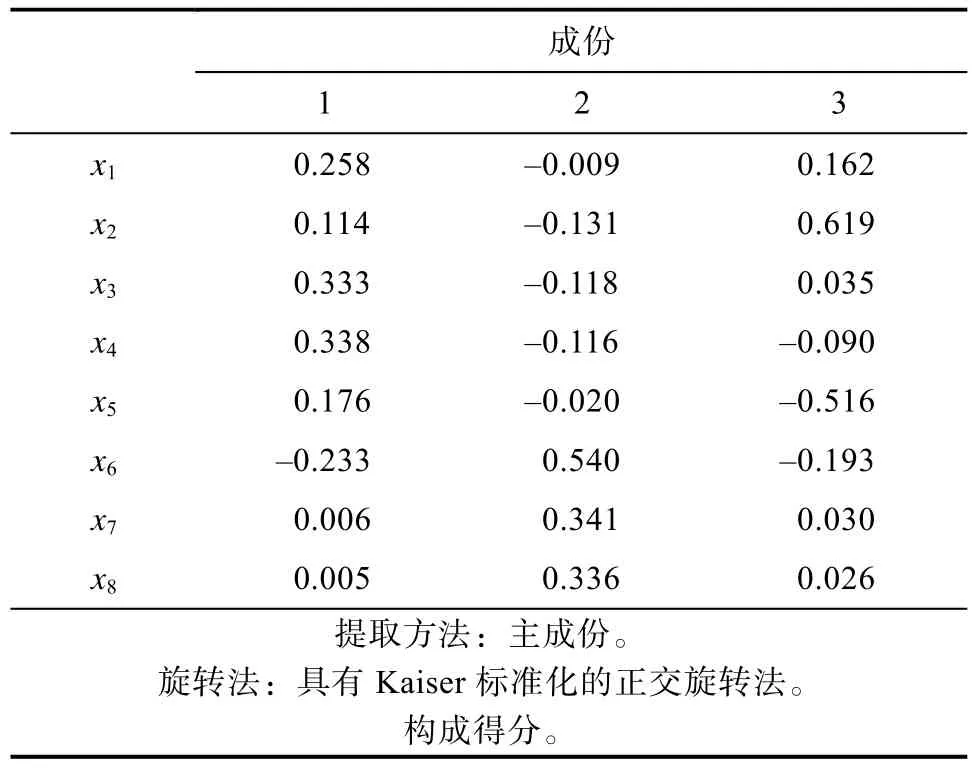
表6 成分得分系数矩阵Tab.6 Component score coefficient matrix

将各地区标准化后的数据代入三个主成分的线性方程，得到三个主成分得分。以每个主成分的方差贡献率为权数对三个主成分进行加权求和，即构建出综合评价模型[12]：Z=0.41224Z1+0.29886Z2+0.18287Z3

把各地区三个主成分得分代入上式，即可得出各地区物流水平的综合得分。分值越大，表明其物流能力越强。负分值并不表示物流发展水平差，分值只反映了物流产业发展的相对强弱。具体见表7。

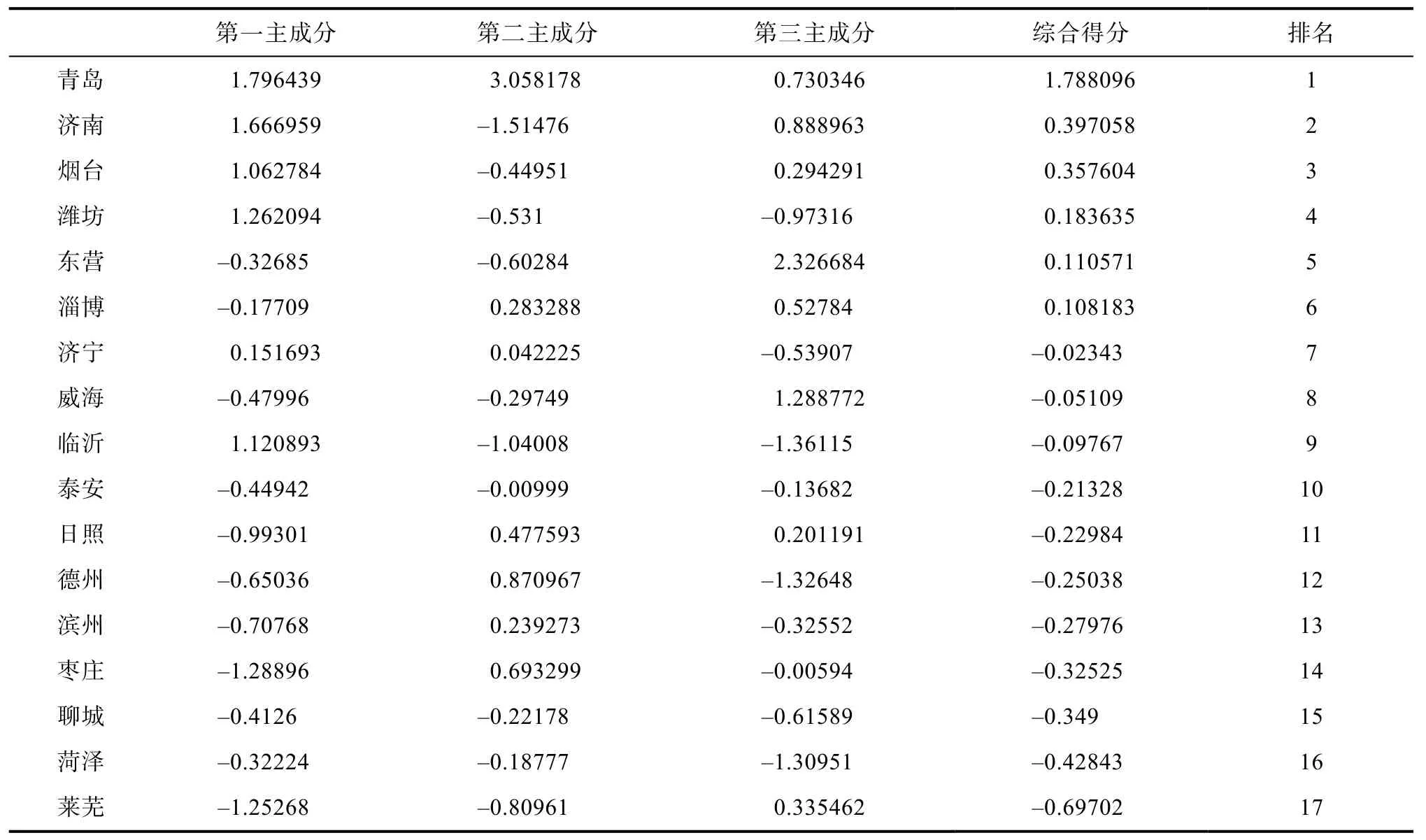
表7 山东省各地区主成分得分Tab.7 Principal component scores of Shandong province

从表7的数据可看出，青岛市排名第一，得分远远领先其他地区。青岛是山东省重要中心城市、沿海开放城市、新一线城市，是全国首批沿海开放城市，国务院批准的山东半岛蓝色经济区规划核心区域龙头城市，其因优越的地理位置以及快速增长的经济情况成为山东省经济发展的核心城市，快速的经济增长推动这青岛市物流产业的快步提升。莱芜经济发展程度相对落后，物流基础设备差，物流需求量低，因此其物流能力排名靠后。另外上表城市中最终得分为正值的有6个，负值的有11个，说明山东省各地区之间发展不平衡，物流产业发展目前总体来说并不容乐观。上表中各城市经济经济水平和其物流能力的排名是相符合的。

3 结束语

本文基于 SPSS对山东省物流产业发展现状进行综合评价，从多种分析结果来看，山东省各城市物流发展差距较大。青岛市，物流发展总得分最高，第一主成分得分1.796439，排名第一，第二主成分得分3.058178，排名第一，第三主成分得分0.730346，排名第四。说明其在经济环境、生产消费、产业结构方面均具有较大优势，为其物流发展奠定了良好的环境基础[13]，远远好过其余城市。第二类城市虽然第一主成分得分略低于青岛，但第二主成分，第三主成分得分排名比较有优势，说明此类城市物流产业发展也较好，物流基础设施建设相对完善，物流发展的环境基础较好。第三类城市在三个主成分上得分均较低，其物流发展综合水平较低。

分析结果表明，经济发展较快的青岛、烟台等地区，物流综合得分较高，经济比较落后的莱芜得分最低。经济发展是物流能力发展的基础，而物流能力的高低是关乎地区未来发展的关键因素。因此，想要提高区域发展水平，必须提高区域物流能力，区域物流能力和区域经济[14]协同发展，加强对物流基础设施的完善程度，加大对物流产业的投资，为区域物流创设一个良好的经济发展环境，从而促进区域经济和区域物流相互进步，共同发展。

本论文存在的不足之处在于缺乏动态性，以后的研究可以着重于从动态的角度分析山东省物流发展情况，做横向对比，将几年之间的物流发展情况进行分析，从而找出17个城市中物流发展最快最好的城市做标杆，以此为基础为山东省物流未来的发展提供有效的依据。