基于深度学习的短时道路交通流量预测研究
2020-07-10郑友康王红蕾
郑友康,王红蕾
(贵州大学电气工程学院,贵州 贵阳 550025)
0 引言
实时、准确的交通流量预测能够为出行者提前规划合理的路线,减缓交通拥堵和空气污染,节约出行时间,因此,对短时道路交通流量预测的研究具有重要的现实意义。杨高飞[1]等人应用ARMA和卡尔曼滤波来对未来短时道路交通流量进行研究,刘钊[2]等提出了用基于时空参数的 KNN算法对序列状态向量进行重建。但是,道路交通流量时间序列具有随机性和高度的非线性,为了更深层次挖掘道路交通流量时间序列的特征,也有学者将目光转向机器学习的支持向量机等方法上,韩志聪[2]等提出了基于GA-SVR模型的短期交通流量预测方法,并取得了比较好的效果。近年来,有越来越多的学者运用深度学习相关方法来进行道路交通流量的预测,刘明宇[3]等提出了一种基于GRU深度学习模型的交通流量预测研究方法,预测精度还是不高。提出的基于长短时记忆模型的方法,实现对道路短时交通流量的预测,提高了道路交通流量预测的准确性。
1 模型设计
1.1 长短期记忆模型(LSTM)
长短期记忆模型(LSTM)是一种特殊的 RNN模型,是为了解决RNN模型梯度消失的问题而提出的[4]。LSTM 的循环结构由 3个控制门组成,由遗忘门(forget gate)、输入门(external input gate)和输出门(output gate)组成。它的结构如图1所示。

图1 LSTM单元结构图Fig.1 LSTM unit structure
各个门的激活方式为:

其中 g代表逻辑函数sigmond,值域在[0,1]区间内,通过g函数的映射。f代表遗忘门,i代表输入门,o代表输出门,h为神经元细胞输出,c代表隐含细胞状态,p表示tanh函数,构建候选向量[5-7]。
1.2 模型构建
假设时间 t时刻待预测路口横断面交通流量为v(t),嵌入维数为m,时间间隔为p,则有集合x(i)={v(t-p)},v(t-2*p),…,v(t-(m-1)*p)},样本{x(i),v(t)}为一个训练样本,任务是通过模型挖掘历史状态序列数据的特征,预测未来一段时间的路口交通流量[8-9],即 v(t)=h(x(i))。
我们的任务是找出h,如图2所示。

图2 模型结构Fig.2 Model structure
1.3 自适应学习率
深度学习算法使用梯度[10]下降来进行权重参数的更新,在LSTM中,参数更新方式为:

其中ω代表LSTM待优化参数,η表示学习速率,为一常量,E代表传播误差。
梯度下降算法并不能保证使得损失函数达到全局最优的位置,并且随着迭代次数的增多,参数ω的值理论上越来越接近极值点,若使学习率η参数一直保持原值,则在更新参数时可能会跳出极值点范围,进一步,会使得模型失效。为了解决这个问题,笔者提出了一种自适应学习率方法来改进LSTM在权重更新时可能会遇到的“跳出”怪圈,改进为:

其中ig表示损失函数关于ω的第i次偏导数,iη代表第i次更新的学习速率值,代表E代表损失函数。
2 实验设计及仿真分析
2.1 数据的获取
这里选取了安徽省合肥市某路口的道路交通流量数据,时间范围为2016年6.22号到2016年6月30号,去除双休时间,时间间隔为2分钟,嵌入维数为4,得到了899组样本,其中前720个样本作为训练集,后179个样本作为测试集。
2.2 模型的对比和指标选取
本文采用了支持向量回归(SVR),普通长短期记忆模型(LSTM)进行对比,选取了均方根误差(RMSE)两个指标来对模型的质量做出评价,下面给出它的定义:

式中iy代表实际交通流量,iy˙代表模型预测的交通流量,n代表了模型中预测的点的个数。
2.3 结果分析
仿真环境是64位的windows7系统,python版本为3.5.0,使用sublime_text3作为编辑器,keras,sklearn的开发库。对于支持向量回归(SVR),核函数选取非线性函数 RBF,gama=0.2,C=100,选择t=10的交叉验证方法,epochs=10,batch_size=1,LSTM,隐含层神经元数为 156,学习速率常量取0.3,以下是各种算法在同一测试数据集下的预测分布图。
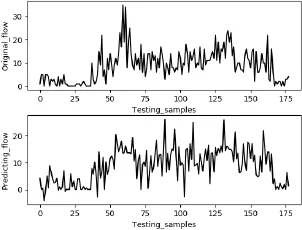
图3 SVR预测结果Fig.3 SVR prediction results

图4 LSTM预测结果Fig.4 LSTM prediction results
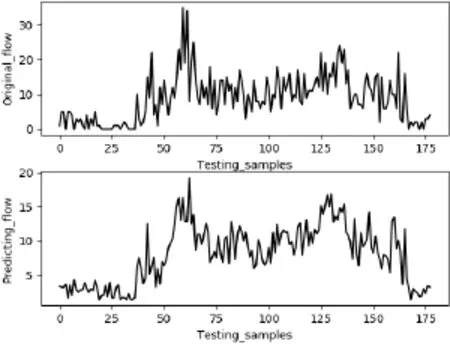
图5 ILSTM预测结果Fig.5 ILSTM prediction results
分析知ILSTM相对于和SVR,LSTM模型在训练集和测试集拥有更好的预测精度,因为它们有更深的层次结构,对交通流量时间序列的特征挖掘更深,这说明LSTM相对复杂的结构能够提升模型的精准度,SVR虽然在训练集上拥有更好的预测精度,但其泛化能力不高,在测试集上表现变差。
三种模型误差对比如表1所示。

表1 三种模型误差对比Tab.1 Error comparison of three models
3 结论
为了提高对研究路口道路交通流量预测的精度,分别尝试了K最近邻回归(KNN),支持向量回归(SVR),普通长短期记忆模型(LSTM)以及改进长短期记忆模型(ILSTM)等算法,仿真结果显示,改进的ILSTM的深度学习算法具有更好的预测精度。可以为安徽省合肥市交警部门的交通疏导以及决策提供依据。
