基于互模糊函数的高亚音速目标声学跟踪方法

陈昭男，付 军，秦亮亮，李 鹏

(1.中国人民解放军91550部队,辽宁 大连 116023；2.中国人民解放军91604部队,山东 烟台 265700)

0 引言

低空高速飞行目标的探测和跟踪是雷达探测技术的盲点之一。 近年来，基于目标声信号的探测和定位技术作为雷达探测技术的补充方案，得到了广泛关注。声探测技术通过被动接收目标发出的声波以确定目标位置，具有隐蔽性强、不易受电磁干扰和可探测低空目标等优点[1]。

根据目标运动速度是否超音速，可将运动目标分为超声速和亚声速两类。对于超声速类目标，其声信号呈现明显的激波特性，主要通过检测激波来实现对目标的跟踪[1]；对于亚声速类目标，目前研究主要集中在对直升机、无人机等低速目标的跟踪[2-3]，对接近声速的高亚音速类目标还未见相关研究。本文主要针对低空高亚音速目标的声学跟踪方法展开研究。在低空低速目标的声学跟踪方法方面，主要采用的方法有时延估计定位法[4-7]、基于瞬时频率估计的目标定位方法[8-9]、空间谱估计定向方法[10-12]等。在目前已知的三大类跟踪方法中时延估计法计算效率高，易于实现，且应用范围广，因此主要针对这一方法展开研究，提出了一种利用互模糊函数的高亚音速目标声学跟踪方法。

1 运动目标时差量的估计方法

1.1 声基阵阵型设计

为了提高隐蔽性，采用被动跟踪体制，即只通过接收运动目标发出的声音来完成定位及跟踪。本文针对窄带声源进行定位研究，对于宽带声源，如果其频谱中含有明显的离散谱，本方法也适用。在此采用无指向性的传感器阵列来实现对目标的定位跟踪，传感器阵列由至少三个传声器组成，各个传声器分别位于不同地点。在采用平面五元十字阵的情况下，目标声源与传感器阵列的几何关系如图1所示。

图1 目标与传感器阵列的几何关系图Fig.1 Geometric diagram of targets and sensor array

通过利用不同传声器接收目标信号的观测量，包括到达时间差(Time Difference of Arrive,TDOA)和到达时间的比例尺差(Scale Difference of Arrive,SDOA)对目标的运动参数进行估计。

假设传感器阵列一共有N个传声器，在传感器阵列接收到的一组信号中，最早到达的一路信号为f0(t)，其对应的传声器称之为基准传声器，其他路信号为fi(t)，i=1,2,…,N-1，第i路信号的时长为Ti，数据采集模块的采样频率为fs，对应的采样周期Ts=1/fs。目标在k时刻的运动参数包括位置坐标[xk,yk,zk]，速度矢量[vx,k,vy,k,vz,k]以及加速度值ak。

由于目标是运动的，不同路信号间的TDOA和SDOA是随时间变化的。对目标运动轨迹进行分段，每段长度为L(单位为m)，在这一段长度内，认为目标的运动参数是不变的。目标运动轨迹是对应到接收信号的，相应地，对各路接收信号也按照相同的时间间隔进行均匀分段。通过对每一段的目标运动参数分别进行估计，即可得到目标的运动轨迹及相关运动参数。

1.2 TDOA和SDOA值估计

假设对目标的速度值大小v有一个先验的约束范围vmin≤v≤vmax，将目标的运动轨迹均匀分为NL段，也就是将对应的各个接收信号按照同样的时间间隔且时间同步地均匀分为NL段，假设信号采样周期为Ts，每段对应的目标运动距离为L，相应的采样点数N0为⎣L/vmaxTs」。在实际应用中，为保证定位跟踪精度，每一段信号中的采样点数目N0不能太少，采样周期Ts和划分段数NL的取值使N0=⎣L/vmaxTs」大于某个预先设定的最小值N0,min。根据后续信号处理算法的实际需求，N0,min的典型值取256或者512。

传感器阵列接收的各路信号组成接收信号向量[f0(t),f1(t),f2(t),…,fN-1(t)]，其中f0(t)为最先到达的基准信号。将目标的运动轨迹均匀分为NL段，也就是将对应的各个接收信号时间同步后，按照相同时间间隔均分为NL段，对分段后的信号向量，在每一段内取N0个采样点，对基准信号和其他各路信号的TDOA和SDOA分别进行估计。采用互模糊函数(Cross Ambiguity Function,CAF)方法进行TDOA和SDOA的联合估计。

假设对于第k段接收信号，目标相对于基准传声器和传声器i的径向速度分别为vr0,k和vri,k。径向速度为目标相对于传声器的速度，相向取正，相离取负。用φik表示传声器i接收信号的第k段相对于基准传声器的SDOA，则SDOA与径向速度的关系为[13]：

(1)

基准传声器的接收信号y0(t)可表达为：

y0(t)=x(t)+n1(t)，

(2)

式中，x(t)为运动目标发出的声音传播到基准传声器的信号，n1(t)为噪声。根据式(2)，传声器i接收的信号可表示为：

(3)

式中，n2(t)为噪声，a为传声器i相对于基准传声器的信号相对幅度增益，τ为传声器i相对于基准传声器所接收信号之间的时差TDOA，φ为传声器i相对于基准传声器的时间伸缩因子SDOA，其表达式如式(1)所示。在得到y0(t)和yi(t)两路信号后，采用互模糊函数法来对τ和φ进行联合估计。y0(t)和yi(t)的互模糊函数CAF表达式为：

(4)

式中，T为信号时间长度。使CAF取得最大值的τ和φ的组合，分别为TDOA和SDOA的最优估计值，选用其作为后续目标跟踪过程所使用的TDOA和SDOA值。

当联合估计TDOA和SDOA时，随着目标的运动，目标相对于传声器的径向速度是迅速变化的，导致SDOA也是快速变化的，因此将目标的运动轨迹划分成小段，在每一段内分别进行TDOA和SDOA的估计。目标的运动轨迹是映射到各路接收信号上的，将各路接收信号划为小段时，采用连续划分的方式，即各个小段是相连的，同时每一小段内的所有信号都参与估计运算。假设最早到达的一路信号为f0(t)，其与传声器i接收信号fi(t)的TDOA和SDOA联合估计表达式为：

(5)

式中，T1为信号段的长度。对于TDOA和SDOA的估计，具体做法是通过对TDOA和SDOA的二维搜索，寻找使两个信号的互模糊函数取得最大值的参数组合，即为该时刻的TDOA和SDOA值。

2 目标运动参数估计

2.1 目标运动参数估计模型

在得到观测参数TDOA和SDOA后，建立目标运动方程和传感器观测方程，对目标运动参数进行估计。假设系统的运动参数为位置坐标及速度矢量，首先根据目标前后时刻运动参数的相互关系，建立目标运动方程：

(6)

式中，a为加速度值，|vk|为k时刻速度模值，加速度值通过初始时刻估计值或者先验值得到，在后续状态更新过程中作为已知值代入目标运动方程中；nk为系统随机输入噪声向量。式(6)给出的是目标匀加速运动时的运动方程。

根据观测量与运动参数的相互关系，建立观测量与运动参数的解析表达式，即为传感器观测方程。当利用目标声音信号到不同声传感器的传播路径差进行定位时，其传感器观测方程为：

i=1,2,…,N-1,

(7)

φik=(c-vr0,k)/(c-vri,k)+χi,

i=1,2,…,N-1，

(8)

式中，[sxi,syi,szi]为声传感器i的位置坐标，[sx0,sy0,sz0]为基准声传感器的位置坐标，ωi和χi为系统观测误差。目标运动方程和传感器观测方程中的噪声量nk，ωi，χi均服从高斯分布。对于速度信息的估计，通过对前后时刻目标位置差分的方法得到。只要建立观测量与运动参数的解析表达式，就得到了传感器观测方程，因此传感器观测方程不限于上述两种。

2.2 模型求解

对于初始时刻运动参数的估计，采用极大似然估计方法。利用传感器观测方程分别构建目标的位置坐标[x0,y0,z0]和速度矢量[vx,0,vy,0,vz,0]的似然函数p(τ/[x0,y0,z0])和p(φ/[vx,0,vy,0,vz,0])，再利用极大似然估计方法对目标位置坐标[x0,y0,z0]和目标速度矢量[vx,0,vy,0,vz,0]分别进行估计。对位置坐标进行极大似然估计为例，对其估计过程进行说明。根据式(7)，系统观测误差ωi服从高斯分布，对于某路信号的时差测量值τi0，单路信号得到的似然函数p(τ/[x,y,z])可表达为：

(9)

式中，σω为系统观测误差变量ωi的方差。采用N路声传感器对目标进行测量，在同一时刻，共得到N-1个测量值，总的似然函数是各路信号得到似然函数式(9)的乘积，因此目标位置坐标的似然函数表达式为：

(10)

在无误差情况下，观测变量τi0与目标位置坐标之间的关系式为：

(11)

在某一位置坐标[x0,y0,z0]附近的区域，将式(11)用泰勒级数展开的方法，用一次多项式近似，得到的近似表达式为：

(12)

将式(12)代入式(10)，可以得到：

(13)

式中，指数项部分F(x,y,z)的表达式为：

(14)

F(x,y,z)是一个二次多项式，可以写成如下标准形式：

F(x,y,z)=a1x2+a2y2+a3z2+a4xy+

a5xz+a6yz+a7x+a8y+a9z+a10。

(15)

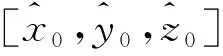
(16)

(17)

式中，i=0,1,…,N-1。根据式(17)，分别将vri,0和vri,k的表达式代入式(8)，即可得到声传感器观测量SDOA与初始时刻目标速度矢量[vx,0,vy,0,vz,0]的数学关系式，依据此关系式即可得到目标初始速度矢量[vx,0,vy,0,vz,0]的似然函数P(φ/[vx,0,vy,0,vz,0])。针对目标速度矢量的似然函数，利用对目标位置坐标进行极大似然估计的相同步骤，采用式(9)～式(16)，即可完成对目标速度矢量[vx,0,vy,0,vz,0]的极大似然估计。在得到初始目标速度后，通过计算前后两个时刻的速度变化率可得到目标加速度的估计值。

在通过极大似然估计方法或者利用先验信息得到初始时刻目标运动参数后，后续时刻的目标运动参数根据目标运动方程和传感器观测方程，采用贝叶斯递推状态估计算法来实现。

3 算法仿真与误差分析

3.1 仿真参数设置

为了验证算法的可行性和准确性，在Matlab仿真环境中，对该方法的性能进行了仿真分析。对于高亚音速飞行目标的模拟，首先从50 Hz声源中提取部分实测信号，再模拟产生其多普勒效应，最后在仿真环境中叠加高斯白噪声。目标运动产生的多普勒频移效应根据目标与传感器的径向速度来进行模拟，假设目标运动方向与目标声波到传感器传播方向的夹角为α，则由运动引入的多普勒频移为vf0cosα/c，v为目标运动速度，f0=50 Hz，c为声速。在实际测得的50 Hz声信号基础上，对于多普勒效应的仿真模拟，采用对信号分段，并对每段信号持续时间(周期)根据多普勒频移进行调整的方式完成，如原信号每段持续时间为12 ms，频率为50 Hz，受到多普勒效应影响后的接收信号频率为60 Hz，则该段信号波形不变，但持续时间调整为10 ms。

3.2 运动参数估计仿真

首先对目标信号特性进行分析。运动目标声信号的时域波形和静止声源的功率谱如图2和图3所示。

图2 亚音速目标声信号波形Fig.2 Signal waveform of subsonic target

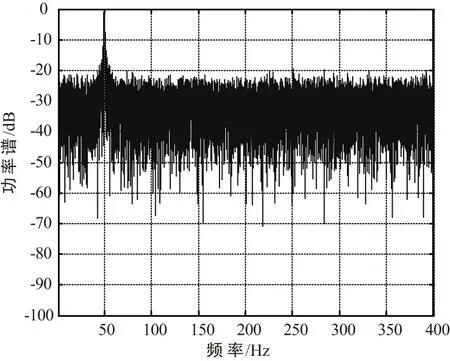
图3 静止声源功率谱Fig.3 PSD of static sound source

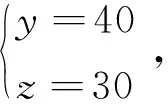
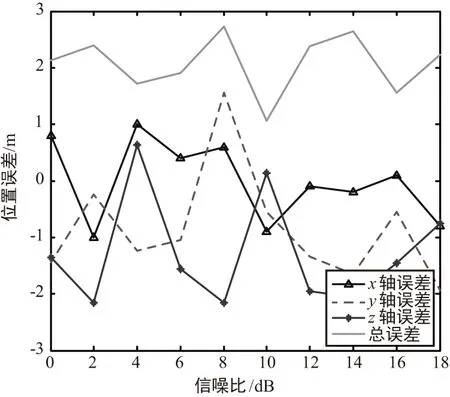
图4 不同信噪比下的目标位置误差Fig.4 Target location error in different SNRs

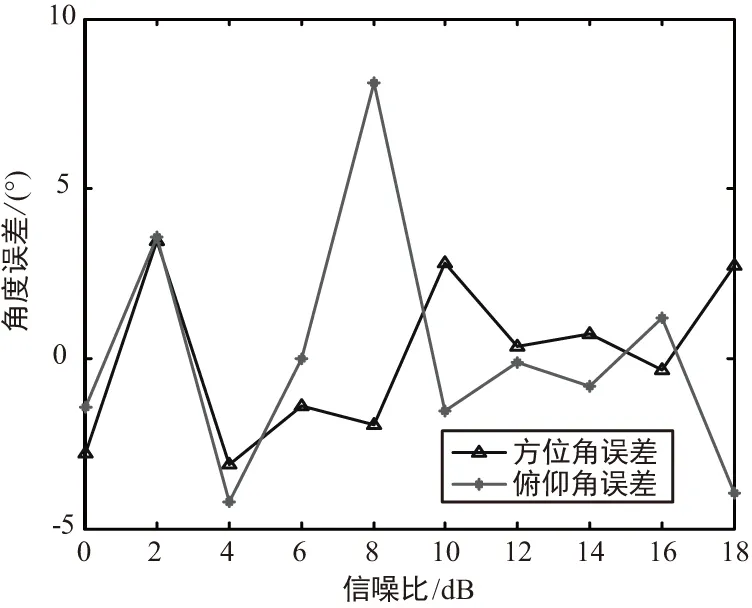
图5 不同信噪比下的目标角度误差Fig.5 Target angle error in different SNRs

通过图4和图5可以看出，无论是目标位置还是角度，在这种情况下，其误差大小均与信噪比关系不大，距离误差维持在2 m左右，方位角误差在5°以内，俯仰角误差相对大一些。上述仿真结果表明该算法可以实现对低空运动目标的稳定跟踪。由上述仿真结果，在上述参数设置下，信噪比不是影响定位精度的主要因素，传声器采样率、传感器阵列结构等因素都对定位精度构成了制约。由图5可见，俯仰角误差明显大于方位角误差，这与所采用的传感器阵列结构有关。传感器阵列都位于同一平面上，各路接收信号对于俯仰角所产生的TDOA不敏感，因此导致其定位误差较大。

在上述仿真参数设置的基础上，首先将传声器采样率提高到256 kHz，在不同信噪比下，对位置和角度误差进行了蒙特卡洛仿真。其对目标定位的位置误差和角度误差与接收信号信噪比的关系如图6和图7所示。

图6 高采样率下的目标位置误差Fig.6 Target location error in large sample rates

图7 高采样率下的目标角度误差Fig.7 Angle error in large sample rates

由图6可知，此时目标位置误差和角度误差均随信噪比的增加而迅速下降，目标位置误差均维持在1.8 m以下，而目标角度误差除了在0 dB处大于2°以外，其余均在2°以下。整体而言，目标位置误差和角度误差与传声器采样率为50 kHz时相比，均出现了明显下降。该仿真结果验证了只有传声器采样率达到一定量级时，目标定位误差才随着信噪比呈现下降趋势。

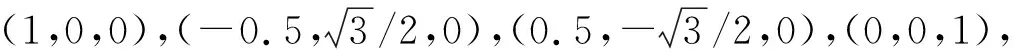
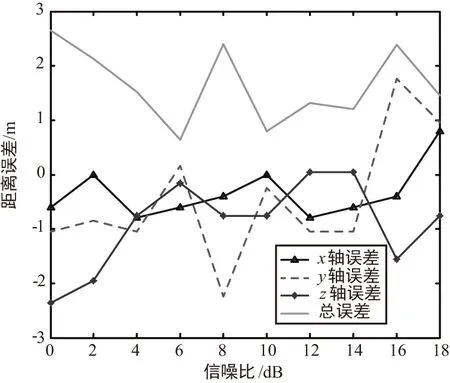
图8 不同信噪比下的目标位置误差Fig.8 Target location error in different SNRs

图9 不同信噪比下的目标角度误差Fig.9 Target angle error in different SNRs

由该仿真结果可见，目标位置误差与第一次仿真结果相差不大，而角度误差，尤其是俯仰角误差产生了较大程度的下降，俯仰角误差均维持在2°以内。该仿真结果表明，传感器阵列在垂直方向上的分布将对俯仰角定位精度产生较大影响，传感器阵列在垂直方向上分布越均匀时，其俯仰角定位误差越小。

综合以上布阵情况，假设基准阵元布设于原点处，设置空间直角坐标系，在x轴正负半轴对称布设两个阵元，其相对于基准阵元的时延分别为τ1和τ3(τ1对应x轴正半轴阵元)，同理y轴正负半轴两个阵元的相对时延分别为τ2和τ4(τ2对应y轴正半轴阵元)，则目标方位角φ与时延估计量的关系为：

(18)

目标俯仰角与时延估计量的关系为：

(19)

通过比较式(18)和式(19)可见，对于分布于水平面的声阵列来说，其目标方位角的估计精度有时延估计量的精度决定，而与阵列大小及声速值无关，而其俯仰角估计精度则同时由阵列大小、声速值以及时延量估计精度共同决定。时延量估计误差主要由环境噪声、各测量通道之间的相位不一致性以及声波在空间中传播的随机起伏等因素引起。环境噪声和传播随机起伏可通过改进算法进行抑制，而测量通道的相位不一致性需要通过改进测量设备，提升各通道相位特性来实现。

4 结束语

本文对亚声速低空运动目标的定位跟踪问题进行了研究，通过对目标辐射声信号的TDOA和FDOA值进行测量，提出了一种基于互模糊函数的目标跟踪方法。该方法基于互模糊函数，首先利用极大似然估计方法或者先验信息得到初始时刻目标运动参数后，后续时刻的目标运动参数根据目标运动方程和传感器观测方程，采用贝叶斯递推状态估计算法来实现。仿真结果表明，该方法可以在较小的位置误差和角度误差范围内，实现对低空运动目标的稳定跟踪。