有障碍物通道内双向行人流的自组织现象

吴 成, 蓝冬恺, 董力耘,2

(1.上海大学力学与工程科学学院上海市应用数学和力学研究所,上海200072;2.上海市力学在能源工程中的应用重点实验室,上海200072)

目前,不同场景下的行人流自组织现象引起了人们的广泛关注[1-2].通道中的行人运动便是一个常见的场景,由于其足够简单,故常被用来研究行人之间的相互作用和集体行为.众所周知,通道内的典型自组织现象是双向人流中自发成行现象.同向运动的行人自动形成队列,因而与反向行人间的冲突显著减少.在许多观测和实验中都能发现成行现象,成行现象可以作为验证行人流模型的定性基准之一.一般来说,微观模型允许描述个体之间的细致的相互作用,因此微观模型更适用于模拟行人的自组织现象.微观模型主要分为2类:①基于力的模型(如社会力模型[3]);②基于规则的模型(如元胞自动机模型[4]和格子气体模型[5]).这2类微观模型都能定性地再现双向行人流中的成行现象.社会力模型是连续的,能够更真实地描述行人运动.在社会力模型中,为了能更细致地描述行人运动,引入了物理接触力这类社会力,如排斥作用、摩擦力和波动等.成行现象的出现是由于行人想减少不必要的减速以及回避的频率[6].在基于规则的模型中,还有几种其他机制,如靠右行走偏好[5]、跟随行为和回避行为[7]等.

为了使模拟结果与经验观测和实验数据一致,人们对社会力模型和元胞自动机(cellular automation,CA)模型进行了大量的改进.Lakoba等[8]提出,在社会力模型中应运用更加真实的参数,并在排斥社会力中引入新的机制,例如记忆效应和密度效应等;Parisi等[9]引入了一种自停止机制,用来防止模拟中行人不断地挤压其他行人的行为;Moussa¨ıd等[10]提出了一种基于启发式的方法,该方法可以利用一些智能规则来评估可行方向和速度;Wang等[11]提出了一种优化的避免碰撞模型,使行人可以在他们的视野中找到一条到达目的地最快的路径;Xiao等[12]提出了一种改进的基于启发式的模型,该模型考虑了行人步行的舒适度,是通过局部密度来表示舒适度;最近,Jiang等[13]把动态导航加入到了社会力模型中行人的决策过程中.从基于规则的模型而言,一些学者对靠右行走偏好[14-15]和换位行为[16-17]对成行现象的影响又进行了深入研究.Nowak等[18]已经对自由流、无序流、成行现象和堵塞的发生进行了定量分析.

元胞自动机模型中的一个重要进展是Burstedde等[19]引进了背景场(floor field,FF)概念.背景场可以分为2种:静态场和动态场.静态场用来指定空间中更具吸引力的区域,例如出口或其他目标[20].静态场的梯度表示每个行人的合理移动方向.此外,Varas等[21]和Huang等[22]还提出了在有障碍物情况下背景场的有效算法.动态场可以用来模拟行人的跟随行为[20].基于背景场的元胞自动机模型的主要优势是提供了一个统一的方法来确定区域内每个行人各自的期望方向.因此,基于背景场的元胞自动机模型得到了许多学者的广泛应用和推广.例如,Suma等[23]建议使用背景场来模拟行人的回避行为;Ma等[24]提出了一个k近邻对流模型,该模型使行人与近邻的固定数目的反向行人产生相互作用;Guo等[25]综合考虑了路程、行人拥堵状况、路线和出口的通行能力,研究了行人对路线选择行为;Tian等[26]将行人自身当作一种可移动的障碍物,因此静态场在每个时间步长都会发生变化;Lu等[27]将行人群体行为的特征也纳入基于背景场的元胞自动机模型.另一方面,Zhang等[28]提出了一个考虑费用势场(potential field,PF)的元胞自动机模型,该模型将从这个元胞到目的地的最小费用定义为元胞的成本势能;Jian等[29]在模型中加入了感知费用势能场和集中力场;Zhang[30]通过考虑导流、压力及其包含的影响提出了一个综合势场,结果表明在模型考虑场内跟随行人的数量后可以促进成行现象的形成;Guo等[31]提出了一种考虑人群速度、密度分布及行人主观意识的PFCA(potential field cellular automation)模型.总之,综合考虑各种因素可以有效地反映行人对路径选择行为以及行人之间的局部相互作用,从而使背景场和势能场都得到不断完善;另外,社会力模型与元胞自动机模型之间其实并非截然不同,一些基于规则的想法同样可以应用于社会力模型.

相比之下,对有障碍物通道内的行人流的研究却比较少.通道中的瓶颈也可以看作是一种障碍.与单向流不同,研究通过瓶颈的双向行人流更加有趣且具有挑战性,其中典型的自组织现象是振荡流,这种现象在社会力模型中可以得到定性的再现[3].然而,对双向流中瓶颈处的定量研究还较少[32-33].除了瓶颈外,可能还存在其他形式的障碍物,如隔栏或圆柱.显然,障碍物的存在会对成行现象的出现产生影响,还可能会出现一些新的自组织现象.此外,在一些特定位置放置行人设施一定情况下会提高通行效率[1].

本工作通过所提出的改进社会力模型[34]研究了加入障碍物的通道内双向行人流.本工作选择了3种典型案例进行了研究:①圆柱等间距分布在中心线上;②具有中心对称分布的双垂直隔栏;③一对安装在水平壁上的对称垂直隔栏.对于前2种情况,本工作在周期边界条件下进行模拟,对于最后一种情况,考虑到现实交通情况,采用了开放边界条件.在每一种情景中,本工作都侧重于研究行人流中的各种自组织现象.由于障碍物的存在,故预测将会出现更为复杂的人群运动特性.另一个有意义的问题是检验障碍物的放置会提高行人的通行效率.

1 改进社会力模型

社会力模型可以较好地再现简单场景下的行人流自组织现象.然而,仅通过最终目的地来指引行人运动是不够的,尤其是在复杂场景下[35].而基于背景场的元胞自动机模型[21-22]可以有效地解决这个问题.因此,把这2种微观模型的优势结合起来,提出了改进社会力模型[34].本模型与社会力模型的区别在于弛豫项中如何确定每个行人的期望运动方向.此外,用视野场代替了动态场,因为视野场在处理行人周围的局部信息时的效率更高.可见,加入视野场的背景场能使确定行人的期望方向能变得更加合理,之前工作中也使用过类似的做法,结果证明这是有效可行的.

社会力模型的运动方程为

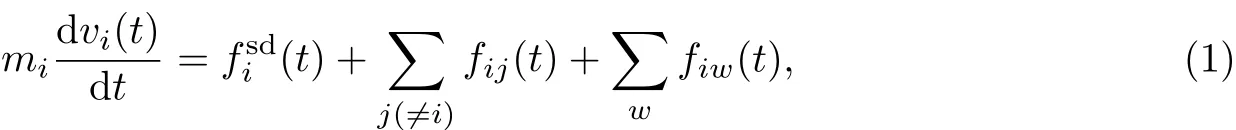
式中:xi(t)为行人i的位置;vi(t)为行人i的实际速度,即vi(t)=dxi(t)/dt;mi为行人i的质量.

方程(1)右边由3项组成,其中第1项为行人经过一段弛豫时间τi后将其实际速度调整到理想速度的自驱力,

式中:ei(t)为期望运动方向;τi为弛豫时间.

计算自驱力的关键在于如何决定一个行人的期望方向,尤其是当周围环境比较复杂的时候.本模型中,背景场被定义在细化的网格上(见图1(a)),网格大小为0.1 m×0.1 m.行人是用一个半径为r的圆表示的,用一个十字标记表示行人的中心.每个行人都有8个运动方向可以选择,分别用数字1∼8表示.选择周围8个元胞的概率是通过静态场S计算得到的[24]:

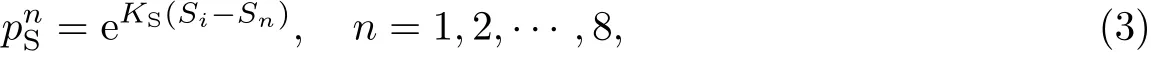
式中:Si为行人i的静态场强度;Sn为周围元胞的静态场强度;KS为静态场系数.

同时,本模型又考虑了行人的视野场.视野场是一个半径为rV的圆形区域,被分割成8个部分,每个部分对应一个可能移动的方向(见图1(b)).视野场的作用与动态场类似,但是比动态场更加高效.视野场的基本思路是行人更倾向于跟随同向的行人,而排斥反向的行人,即“同向相随,异向相斥”.行人选择方向的概率为

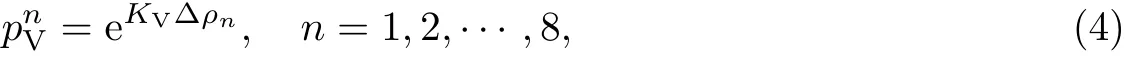
式中:KV为视野场系数;∆ρn为密度差,由该行走方向的扇形区域内同向行人人数减去不同向行人人数的差再除以该圆面积的1得到.

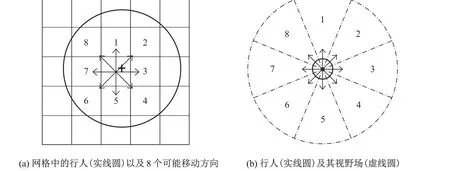
图1 行人运动方向及其视野示意图Fig.1 Schematic diagram of both movement directions and visual field of a pedestrian

行人的移动概率为

式中:ρV为视野场中行人的密度.当ρV趋向于0时,KS达到最大值,此时行人i会更倾向直接走向目的地.当ρV增加,KS会减小,行人的运动会受到视野场内其他行人的影响.

方程(1)右边第2项为行人i与其他行人j之间的作用力,包括社会力和物理接触力

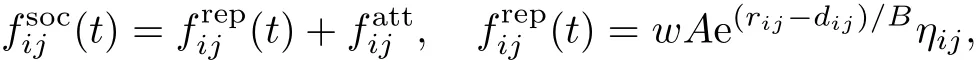
式中:A和B为常数.

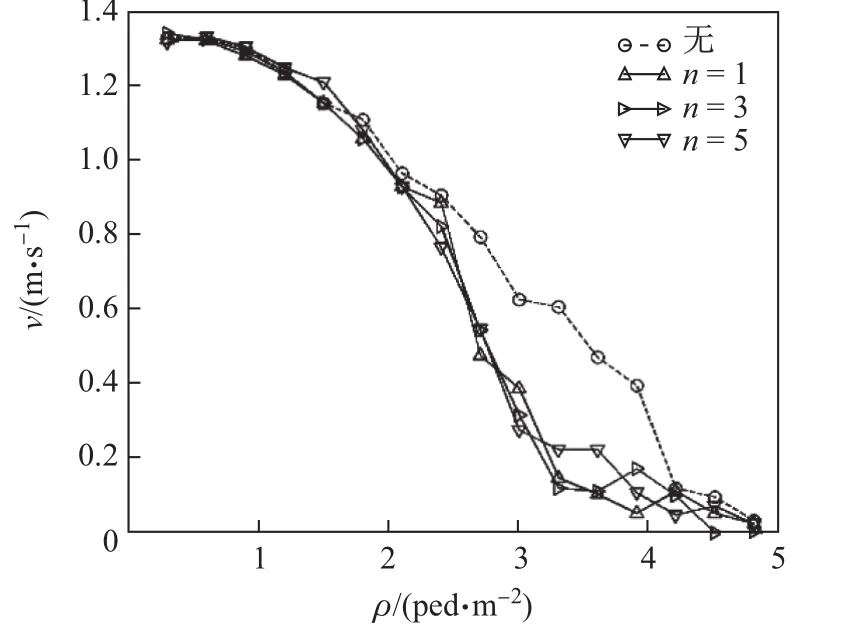
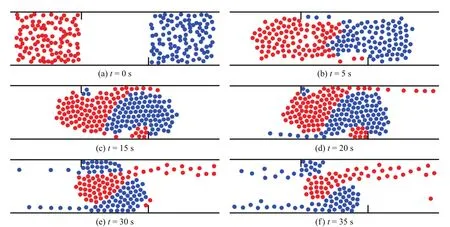
物理接触力仅在行人间有身体接触时(dij

行人与墙和其他障碍物之间的作用和行人之间的相互作用相似,参数值也和行人之间相互作用的参数值一样.模型的更多细节详见文献[34].

2 数值模拟和讨论

本工作对有障碍物的通道内行人对流中的自组织现象进行了模拟研究.模型中的参数设定如下:对于每个行人,半径rp=0.2 m,质量m=80 kg,期望速度v0=1.34 m/s,弛豫时间τ=0.5 s.对于视野场,视野场半径rV=1.5 m,视野场系数KV=1.13.静态场常数K0=0.5,H=5.0.社会力和物理接触力的参数分别为A/m=1.8,B=0.1,k/m=150,κ/m=5.本模型中的这4个参数与Kretz等[36]的接近并且值更小,这能使所得到的物理接触力会更加合理,可以在模拟中采用更大的时间步长(如0.1 s).通过和Seyfried等[37]的疏散实验做比较,对模型中的参数进行校准.模拟结果与他们的实验数据非常吻合[34].此外,本工作还计算了单向和双向行人流的基本图,发现在单向流情况下基本图与实测数据[38]吻合较好,特别是在中等密度范围内,但是双向流的基本图会略大于实测数据[39].此外,在一定的密度范围内双向流的流量要大于单向流的流量,这在一定程度上支持Kretz等的结论[40],表明改进的社会力模型可以较好地反映行人流的基本特征,故将其进一步应用于更复杂情况的研究.

2.1 圆柱等距分布在中心线上

本次模拟中,通道宽4.8 m,长14.0 m,在通道的中轴线上等距放置多个半径的圆柱,采用的是周期性边界条件,即行人从一侧离开通道,又立即从另外一侧进入通道.初始时刻,行人随机分布在通道中.图2为不同个数圆柱形障碍物下行人平均速度与密度之间的关系图,图中还加入了没有放置圆柱的情况作为对比.从图中可以发现,速度会随着行人密度的增大而减小.当密度小于2.1 ped/m2时,4条曲线无明显差异.在低密度区域会出现自有流和成行现象.当放置圆柱体以后,运动方向相反的行人会彼此分开,沿着水平壁移动.随着行人密度的进一步增大,在有圆柱情况下行人的平均速度要比没有圆柱时行人的平均速度下降得更快.结果表明,此时放置圆柱会导致拥堵变得更加严重.在高密度区域,行人流趋于饱和.没有放置圆柱时,成行现象仍会发生.但如果放置了圆柱,会更容易导致堵塞现象的发生,此时行人速度会下降得更快.当行人密度超过4.2 ped/m2时,即使没有放置圆柱人流也是非常拥挤,从而使得4条曲线之间的差异可忽略不计.

图2 不同个数圆柱形障碍物下行人平均速度与密度关系Fig.2 Average velocity as a function of density with different numbers of cylinders

图3 不同时刻的行人分布斑图(ρ=3.0 ped/m2)Fig.3 Snapshots at different times(ρ=3.0 ped/m2)

图4 ρ=3.0 ped/m2时行人分布斑图Fig.4 Snapshots for ρ=3.0 ped/m2

图3 为不同时刻的行人分布斑图,其中蓝(红)色实心圆代表向左(右)运动的行人,而黑色实心圆则代表圆柱.初始时刻,密度为3.0 ped/m2的行人随机分布在通道内(见图3(a)).从图3(b)中可以看出,运动方向相同的行人会迅速聚集在一起.在高密度区域(ρ>2.4 ped/m2),这些圆柱会变成障碍物,使得局部堵塞发生的概率变大.由于圆柱的存在,即使只有一个圆柱,也会使成行现象的形成变得困难(见图4(a)).因此,圆柱数量对平均速度并没有明显影响.圆柱的存在会使以其为中心的周围区域内行人变得拥挤,且会阻碍两边行人的运动.在高密度区域,很少能观察到成行现象的出现(见图4(b)).成行现象发生的概率会随着行人密度的增大而减小.Helbing等[1]曾指出,当不耐烦的行人试图超过其他人时,这样设置圆柱可以有效地稳定住2个方向的成行.然而,模拟中所有行人都是一样的,因此在这种情况下串列圆柱这样的措施并不能起到明显的稳定作用.另一方面,初始条件和边界条件也会对成行现象的形成有明显的影响,特别是在高密度区域.当行人数量足够大的时候,随机分布的行人很难快速成行.而圆柱的存在容易导致局部拥塞的发生,并且堵塞区域会越来越大.此外,行人进入通道的方式也是影响因素之一.如果不同方向的行人都各自从一侧进入通道,就容易观察到图4(b)中的成行现象.

2.2 具有中心对称分布的双垂直隔栏

本次模拟中通道的大小与2.1节中的相同,采用的仍然是周期性边界条件.本工作在通道中放置了2个长度都为1 m且对称分布的垂直隔栏.2个隔栏的水平距离为7 m.隔栏中心与中心线的垂直距离y分别为0,0.5,1.0和1.9 m.在行人密度为2.0 ped/m2时,距离y不同的行人分布的差别如图5所示.当y=0 m时,可以很容易观察到成行现象(见图5(a));当然,有时也会出现全部堵塞的情况(见图5(b)).另外,在y=0 m时,2个隔栏之间的区域很少会有行人经过.随着y的增大,2个隔栏之间的区域通过的行人也逐渐变多,会慢慢出现成行现象.当y=0.5 m时,由于左侧有行人堵在隔栏处,因此会观察到局部堵塞;右侧的行人沿着墙壁走,则没有发生拥堵(见图5(c)和(d)).当y=1.0 m时,隔栏之间的距离几乎等于隔栏和最近的墙之间的距离,此时,可以观察到成行现象且为3行(见图5(e)和(f)).当y=1.9 m时,每个隔栏的一侧都是和水平壁相连的,因此行人必须穿过这2个隔栏的中间区域.此时,成2行和成3行现象都可以被观察到(见图5(g)和5(h)).

图5 ρ=2.0 ped/m2,t=400 s时不同偏移距离的人群空间分布斑图Fig.5 Snapshots at t=400 s with different settings of two fences(ρ=2.0 ped/m2,t=400 s)

在不同的间距y时,平均速度与行人密度之间的关系如图6所示.平均速度会随着密度的增大而减小.通道缩减比γ为2个隔栏在垂直方向上的投影除以通道的宽度.当y=0 m时,γ≈0.21.当行人密度小于1.5 ped/m2时,有隔栏的曲线与没有隔栏的曲线基本一致.此时,行人会自发地避开隔栏并沿着水平壁前进,这与放置了圆柱的情况很相似.在其他3种情况下,2个隔栏并不在一条直线上,此时y>0 m,γ≈0.42.可见,3种情况的通道缩减比相同,此时隔栏会对行人的通行产生较大阻碍作用,甚至在低密度情况下都会导致速度减小.不同位置的2个隔栏在一定程度上会影响通行效率.当行人密度超过1.8 ped/m2,y=0 m时的曲线下降速度会大于y>0 m的情况,这是因为此时很容易形成全局拥堵(见图5(b));当行人密度超过4 ped/m2时,此时通道内拥塞严重,这些曲线没有表现出明显的差异.

图6 相同大小、不同位置双垂直隔栏下行人速度与密度关系Fig.6 Average velocity as a function of density with different setting of two fences

2.3 一对安装在水平壁上的对称垂直隔栏

在本次模拟中,设置通道长20.0 m,宽4.8 m,分别在上、下水平壁上安装了一对长度相同的垂直隔栏,其水平距离是8.0 m.初始时刻,行人随机分布在通道两侧的长方形区域且密度相同,2个隔栏间区域没有行人分布.模拟中采用的是开放性边界条件,即行人一旦超过出口边界,就从系统中移除.图7为行人密度(定义为在通道一侧的人数除以该侧矩形分布区域的面积)为3.5 ped/m2时不同时刻的人群分布斑图.在t=5 s时,两侧的行人在中间位置开始有了接触,但是此时他们没有完全混合.同向的行人会成群结队一起移动.在t=35 s以后,运动方向相反的行人完全分开,不再阻碍彼此的移动.当所有行人离开通道时,得到行人的运动总时间.由于隔栏安装在水平壁上,故会阻碍行人沿着墙壁移动.

本工作分别模拟了在行人密度为3.5 ped/m2时,3种不同的隔栏距离(l=0.4,0.7,1.0 m)时的行人运动.对每一种情况都进行了50次模拟,然后取平均值得到平均行程时间和发生拥堵的概率,结果如表1所示.模拟数据表明,随着隔栏长度的增加,平均行程时间会先减少后增多.当隔栏较短的时候,平均行程时间会有所减少;然而,随着隔栏的加长(如l=1.0 m),平均行程时间会大大增加,表明当隔栏较长时隔栏会对行人产生较大的阻碍作用.然而,虽然进一步增加隔栏长度会降低通行效率,延长行程时间,但在一定程度上能够减小堵塞发生的概率,这可以从行人的分布斑图中看出.由于隔栏的存在,使得人群很难发生正面冲突.事实上,隔栏有助于不同方向人群的分离,可以明显减少拥堵发生的概率.但是与此同时,长隔栏会阻碍双向行人流,从而导致中心区行人密度变高,但不同方向人群的分离较难形成完全堵塞.

图7 不同时刻的行人分布斑图(l=0.7 m)Fig.7 Snapshots at different times(l=0.7 m)

表1 初始密度为3.5 ped/m2时不同长度垂直隔离栏的平均行程时间及拥堵概率Table 1 Average travel time and probability of congestion for different lengths of fence when the initial density is 3.5 ped/m2

3 结束语

本工作利用改进的社会力模型,对有障碍物的通道内的行人流自组织现象进行了研究.一些行人设施(如柱子或安全隔栏)都可视为某类障碍物.在周期性或开放性边界条件下,本工作分别对放置在不同位置上的圆柱、隔栏等障碍物进行了模拟,发现成行现象仍是通道内双向行人流的主要现象.然而,由于障碍物的出现,行人的自组织现象变得更加丰富.在周期性边界条件下,障碍物往往会引起堵塞,导致平均速度降低.如果通过在特定地方放置障碍物可以使得行人在高密度下快速且稳定成行,能较好地提高步行效率.在开放性边界条件下,在水平壁上设置较短的垂直隔栏可以减少通行时间.此外,这样设置2个隔栏还可以使出现堵塞的概率变小.但值得注意的是,当隔栏长度超过某一临界值时,则会增加行人的通行时间.对于有障碍物的通道内的双向行人流,还需要做更多工作来全面揭示其整体特性.