基于决策树的流数据分类算法综述

韩成成,增思涛,林 强,曹永春,满正行

(1.西北民族大学 数学与计算机科学学院,甘肃 兰州 730124；2.西北民族大学 动态流数据计算与应用实验室，甘肃 兰州 730124；3.西北民族大学 中国民族信息技术研究院,甘肃 兰州 730030)

0 引言

随着信息通信技术(Information and Communication Technology,ICT)的日益成熟，物联网和无线通信已经广泛应用于工农业生产、生态环境保护、公共安全监测和人体健康跟踪等领域，用以实时记录并传输状态数据.

不同于可长期存放在大容量存储设备中的静态数据，承载实时状态及其变化的数据具有数量无限、有序到达和富含变化的特征，形象地称作流数据(Streaming data)或数据流(Data stream).正是因为流数据无限且实时到达，所以需要给予实时响应.

从数据挖掘的角度讲，流数据的处理包括分类、聚类、关联规则提取、序列模式发现和异常检测.其中，流数据分类用于将当前数据流(段)划分到某个事先确定的类别当中，是流数据挖掘的重要研究分支，已经引起了学术界的普遍关注.

基于传统静态数据挖掘技术开发流数据分类模型、算法和方法是学术界普遍采用的做法，其中决策树在流数据分类研究中扮演着重要角色.目前，学术界已经提出了一批基于传统决策树的流数据分类算法，用于不同应用领域的流数据实时分类.

为全面概述基于决策树的流数据分类算法，本文首先简要介绍数据挖掘及主要任务、流数据及其特征；然后，依照算法是否考虑概念漂移将现有工作划分为两大类，针对每一个算法，给出其主要工作流程、优缺点和典型应用；最后，基于现有研究，指出基于决策树的流数据分类算法存在的研究挑战和未来的研究方向.

1 数据挖掘及流数据概述

1.1 数据挖掘及其主要任务

数据挖掘(Data Mining)是人工智能和数据库领域的热点研究问题，在数据库中的知识发现(Knowledge Discovery in Database,KDD)中扮演着重要角色.数据挖掘就是要从随机产生的、富含噪声的大量不完整数据中获取事先未知但潜在有用的信息和知识，以提取出数据的模型及数据之间的关联，进而实现数据变化趋势和规律的预测.

数据挖掘主要包括数据准备、规律寻找和规律表示三个步骤.其中，数据准备从相关的数据源(如商品交易记录、环境监测数据、经济运行数据等)中选取所需的数据，并经清洗、转换、整合等处理生成用于数据挖掘的数据集；规律寻找应用某种方法(如机器学习和统计方法)发现数据集中隐含的规律；规律表示以用户尽可能理解的方式(如可视化)将从数据中发现的规律表示出来.

数据挖掘的任务主要包括分类、聚类、关联规则挖掘、序列模式挖掘和异常点检测.其中，分类(Classification)是指通过在给定的一组已标记数据集上训练模型，预测未标记的新数据所属类别的过程.分类问题可形式化表示为：给定由n个数据构成的集合I= {x1,x2,…,xn}以及这些数据的m个类别集合C= {y1,y2,…,ym}，其中m≤n，求解映射y=f(x)，使得任意xi∈I，且仅有一个yi∈C对于yi=f(xi)成立，称f为分类器.在机器学习(Machine Learning)领域，分类问题属于监督学习(Supervised Learning)的范畴.

不同于分类问题，聚类(Clustering)[1]能够在不给定数据标签(Lable)的情况下，实现数据的类别划分.由于聚类操作不需要对输入数据做预先标记处理，完全根据数据自身的属性实现类别的划分，因此属于无监督学习(Unsupervised Learning)的范畴.关联规则挖掘(Association Rule Mining)[2]用于发现事物(如商品的购买)之间的某种关联关系.序列模式挖掘(Sequential Pattern Mining)[3]是从序列数据库中发现高频子序列的过程.异常点检测(Outlier Detection)[4]用于自动发现数据集中不同其他数据的“异常”数据.

1.2 流数据及其特性

流数据(Streaming Data)，也称数据流(Data Stream)，是不同于静态数据的新的数据形态，它随着时间的推移而不断产生.令t表示时间戳，可将流数据形式地表示为：{…,at-1,at,at+1,…}，其中at为t时刻产生的数据[5].概括而言，流数据具有如下主要特性[6]：

1)实时性：流数据实时产生和到达.例如，在实时监测系统中，随着时间的推移不断有新的数据产生.

2)时序性：数据的到达顺序由其产生的时间先后顺序所确定，不受应用系统的控制.例如，在股票交易系统中，前后两位消费者购买股票A和B的顺序是时间上确定的.

3)多变性：数据的分布是动态变化的，例如，股票的价格会随着市场的动态变化而随之改变.

4)潜在无限：流数据是现实世界的真实记录，因而具有无限性，例如，用于环境监测的传感器网络，监测过程的持续进行使得记录的流数据不断增加.

5)单趟处理：流数据一经处理，不易甚至不能被再次取出，因为流数据的存储代价昂贵，通常一经处理就被丢弃.

除了上述特性外，流数据还时常伴有概念漂移.概念漂移(Concept Drift)是指流数据随时间推移而发生改变的现象，它的存在严重影响着算法的分类性能.如图1所示，若c1和c2代表两种不同的概念(对应于分类问题的类别)，常见的概念漂移主要有如下几种类型[7]：

1)突变型(Sudden)：概念漂移立即发生且不可逆转，如图1(a)中的c1立刻且永久地改变为c2.

2)增量型(Incremental)：概念漂移平稳缓慢且不可逆地产生，如图1(b)中的c1逐渐且持久地改变为c2.

3)渐变型(Gradual)：概念漂移缓慢且不可逆地产生，但中间可能存在往复，如图1(c)中从c1改变为c2的过程中经过了几次往复.

4)可恢复型或暂时型(Recurring)：从一个概念暂时改变为另一个概念且经过一段时间后会恢复到原始概念，如图1(d)中c1暂时改变为c2后又恢复到c1.

5)罕见型(Blip)：概念的异常改变，如图1(e)中c1是异常，而非真正改变到c2.

6)噪声型(Noise)：数据的随机波动，不是真正的概念漂移.

图1 概念漂移的主要类型

由于传统分类算法只能处理可供多次访问的有限静态数据，与流数据的处理要求不相一致，因此，传统分类算法不能直接用于解决流数据的分类问题.为了实现流数据的分类，现有研究通常在传统分类算法的基础上加入适应流数据处理要求的相关功能.

决策树作为一类经典的传统分类算法，能够基于已知数据构建具有多个分支的树状模型，实现数据的分类与预测.与神经网络等其他方法相比，决策树具有较低的时间复杂度和较好的分类性能[8].当前，学术界已经提出了大量基于决策树的流数据分类算法.因此，为了确保完整性，本文在详细介绍基于决策树的流数据分类算法之前，先对传统决策树分类算法做一简要概述.

2 传统决策树分类算法

决策树分类过程通过应用一系列规则，实现对数据的分类.依据树中最优划分属性选择的不同，决策树分类算法主要有ID3和C4.5两类算法.此外，还有用于同时解决分类和回归问题的CART算法.本文首先描述决策树的构造过程，然后分别介绍ID3、C4.5和CART算法.

2.1 决策树

决策树是由根结点、内部结点和叶子结点构成的树状结构.其中，根结点包含了待分类样本的全集，内部结点对应于测试属性，叶结点对应于决策结果.算法1给出了决策树的构造过程[9].

算法首先从根结点开始，根据属性的取值将样本数据分成不同的子结点(从第1行到第7行)，直到当前结点属于同一个类或者取相同的属性值；然后根据属性的取值，计算得到最优划分属性并将该属性作为当前结点；接着递归调用此方法，直到当前结点属于一个类或者没有属性可以划分，算法停止并完成决策树的构造.

算法1的核心步骤是最优划分属性的选择(第8行)，通常以信息增益、信息增益率和基尼指数作为其选择依据.其中，信息增益是指属性划分前后熵(熵是度量样本中属性不确定性的指标)的差值，信息增益率是指信息增益与某一特征熵的比值，基尼指数是指样本被选中的概率与样本被错分的概率的乘积.

算法1：TreeGenerate_DT(D,A)

Inputs：D= {(x1,y1),(x2,y2),…,(xm,ym)} ——训练集；

A={a1,a2,…,ad}——属性集

Output： 以node为根结点的一棵决策树

Process：

1.生成结点node；

2.ifD中样本全属于同一类别Cthen

3. 将node标记为C类叶结点；return

4.endif

5.ifA=∅orD中样本在A上取值相同then

6. 将 node 标记为叶结点，其类别标记为D中样本数最多的类； return

7.endif

8.从A中选择最优划分属性a*；

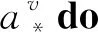
11.ifDv为空then

12. 将分支结点标记为叶结点，其类别标记为D中样本最多的类；return

13.else

14. 以TreeGenerate (Dv,A{a*})为分支结点

15.endif

16.endfor

2.2 决策树分类算法

如前所述，因最优划分属性选择的不同，决策树分类主要有ID3、C4.5和CART等几类.其中，ID3采用信息增益，C4.5采用信息增益率，CART采用基尼指数.

2.2.1 ID3算法

ID3算法[10]运用信息熵理论，每次选择当前样本中具有最大信息增益的属性作为测试属性a*.令pk代表样本集D中属于类别k样本的比率，|y|代表类别数，信息熵可计算如下：

(1)

虽然ID3算法有着清晰的理论基础，但是，每个属性的取值一定程度上影响着信息增益的大小，因而计算训练集的信息增益就会出现偏差.此外，ID3算法对噪声较为敏感，而且当训练集增加时，决策树的规模也随之增加，不利于渐进学习.

表1 西瓜数据集

以表1给出的数据集[11]为例，运用信息熵理论构建一棵判断是否为好瓜的决策树.其中，类别数|y|=2，即有好瓜和差瓜两类，正例(好瓜)p1= 8/17，反例(差瓜)p2= 9/17.根据式(1)计算根结点的信息熵为：

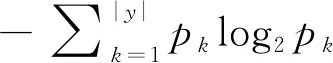
=0.998

计算当前属性集合{色泽，根蒂，敲声，纹理，脐部，触感}的信息增益，以属性“根蒂”为例，它有3个可能的取值：{卷缩，稍蜷，硬挺}.通过该属性对样本集进行划分，得到“根蒂=卷缩”、“根蒂=稍蜷”、“根蒂=硬挺”.其中，在“根蒂=卷缩”中，正例占p1=5/8，反例占p2=3/8；在“根蒂=稍蜷”中，正例占p1=3/7，反例占p2=4/7；在“根蒂=硬挺”中，正例占p1=0，反例占p2=1.根据式(1)可计算出根蒂划分后所获得的3个分支的信息熵为：

E(根蒂=硬挺)=0

最后，可计算出属性“根蒂”的信息增益为0.143.类似地，计算出所有其他属性，找到信息增益最大的是“纹理”，即把“纹理”作为根结点，再对“纹理”的各个分支做进一步划分，最后即可得到判定西瓜好差的决策树.

2.2.2 C4.5算法

C4.5算法[12]虽然继承了ID3算法的优点，有着与ID3相同的算法思想，但又有如下几个方面的改进：

1)用信息增益率而非信息增益作为划分属性选择的依据.

2)在树的构建过程中做剪枝处理.

3)可以对连续属性进行离散化处理.

4)能够对不完整数据进行处理，即可应用于缺失值的处理.

信息增益率主要指在信息增益的基础上引入分裂信息值，信息增益率定义如下：

(2)

其中，G(D,a)是信息增益，IV(a)是属性a的分裂信息.例如，对表1西瓜数据集，有IV(触感)=0.874(V=2)，IV(色泽)=1.580(V=3).

由于信息增益倾向于那些有着更多取值的属性，为了降低这种因素的影响，C4.5采用信息增益率选择划分属性.首先选择信息增益高于平均水平的属性，然后从中选择增益率高的属性.但是，在树的构建过程中，需要对数据集进行多次顺序扫描和排序，因而导致较高的时间复杂度.虽然C4.5同ID3解决类似的问题，但C4.5的准确度更高.

2.2.3 CART算法

针对C4.5算法时间复杂度偏高的不足，Breiman等[13]提出了一种分类回归树算法(Classification And Regression Tree,CART)，该算法由决策树的构建和决策树的剪枝两部分构成.其中，决策树的构建过程就是生成二叉决策树的过程.CART算法既可以用于分类，也可用于回归；既可处理离散问题，也可处理连续问题.

CART采用基尼指数选择划分属性，基尼指数越小，数据集的纯度越高.基尼纯度表示在子集中正确选择一个随机样本的可能性.基尼指数定义如下：

(3)

其中，G(Dv)是样本集中的随机样本.

CART可充分运用全部的数据，能够处理孤立点、空缺值.需要注意的是，CART更适用于较大的样本量，相反，当样本量较小时模型不够稳定.

3 基于决策树的流数据分类

基于传统决策树算法，针对流数据的特性，学术界提出了一系列基于决策树的流数据分类算法.根据算法是否考虑流数据中的概念漂移，本文将基于决策树的流数据分类算法分为不含概念漂移的算法和包含概念漂移的算法两大类.

3.1 不含概念漂移的分类算法

快速决策树(Very Fast Decision Tree,VFDT)是不含概念漂移分类算法的典型代表，也是基于决策树的流数据分类算法的基础.基于VFDT，学术界提出了一系列分类算法，主要包括VFDTc、FVFDT、ocVFDT、VFDTs、uVFDTc和SVFDT等.

3.1.1 VFDT算法

Domingos和Hulten[14]提出了VFDT算法，该算法采用信息熵和基尼指数作为选择分裂属性的标准，以Hoeffding不等式[15]作为判定结点分裂的条件.VFDT算法的详细流程见算法2.

算法2：TreeGenerate_VFDT(T,G,δ,τ)

Inputs：T——离散流数据；

G——信息增益；

δ——置信度；

τ——分裂系数

Output：动态决策树

Process：

1.初始化决策树，此时只包含根结点root

2.for所有的训练样本do

3. 样本从根结点开始，按照最佳属性选择分支，直至到达叶子结点；

4. 更新叶子结点的统计信息(初值设为0)

5. 更新叶子结点的实例数(nl)

6.ifnlmod nmin=0 and 实例不属于同一个类，其中nmin是人为设定阈值

7. 计算该叶子结点l所有属性的信息增益Gl

8. 设Xa是Gl最大的属性

9. 设Xb是Gl次大的属性

10. 计算Hoeffding值

11.ifXa≠Xφand (Gl(Xa)-Gl(Xb)) >εORε<τthen

12. 叶子结点将作为内部结点，属性Xa作为该结点的决策属性

13. 由Xa的取值数目确定新叶子结点数目

14.for所有的分支do

15. 生成新的叶子结点，同时含有分裂结点

16.endfor

17.endif

18.endif

19.endfor

算法2中的信息增益与决策树算法中的定义相同，在决策树的叶子结点中存储数据的统计信息，用于信息增益的计算.该算法依据属性不断划分结点，叶子结点的统计值会随着在样本的遍历而不断更新.

Hoeffding边界能够很好地解决流数据样本过多的问题，其形式化定义如下：

(4)

其中，R代表信息增益的范围，n代表观察值，1-δ代表可信度.

VFDT的一个典型应用是通过统计高校的Web页面请求流，预测高校在将来请求哪些主机和页面.首先将日志分割成一系列相等的时间片，通过在一定时间内访问主机的情况，建立VFDT算法模型，从而预测未来访问主机的情况.

VFDT处理流数据时效果良好，且在时间复杂度和准确度上要优于传统的分类算法.该算法还解决了Hoeffding树没有提到的实际问题，即当两个属性的信息增益近似相等时，权衡两个属性需要花费大量的时间和空间，而VFDT提供了一个人为设定的阈值来解决这种问题.但VFDT不能处理概念漂移问题，同时，此算法没有考虑处理具有连续值属性的问题.

3.1.2 基于VFDT的扩展算法

针对VFDTc算法计算开销大的不足，Wang等[19][20]提出了模糊VFDT算法FVFDE(Fuzzy VFDT).该算法采用模糊决策树T-S模型分类方法，首先利用T算子计算出所有叶结点的类别隶属度，然后利用S算子计算出该样本对所有类别的隶属度，最后利用去模糊化方法确定该样本的最终分类.FVFDT减少了算法的时间复杂度，有效解决了噪声问题，提高了分类精度.

由于流数据分类属于监督学习的范畴，同传统的分类问题一样，数据标记依然是流数据分类需要解决的耗时而棘手的问题.文献[21]在VFDT的基础上提出了一种单类快速决策树分类算法ocVFDT(oneclass VFDT)，该算法沿着树遍历样本到达叶子结点，结点处可生长出新的叶子.对于结点上的每个可用属性，算法计算信息增益.如果满足分割条件，则生成新的叶结点.在计算新叶结点时，正样本和未标记样本的计数均来自父结点.即便是当流数据中有80%的样本尚未做标记的情况下，算法仍然具有出色的分类性能.该算法在信用欺诈检测的案例中，将造成不良经济影响的用户行为视作正样本，而那些尚未造成不良影响的行为可视作未标记的样本.此外，ocVFDT算法也可用于网络入侵行为的检测.

VFDTs算法[22](VFDT stream)是专为流数据问题而设计的增量式决策树，该算法在VFDT的基础上进行了改进，能够处理非常复杂的数据(如维度较高的数据).当到达叶结点时，算法将更新所有统计信息.如果有足够的统计支持度，那么叶子将被转换为决策结点，并创建两个新的子代.VFDTs算法应用广泛，例如CRPGs游戏，玩家在每一轮战斗中有多种选择，使得游戏中的决策变成了一项复杂的推理任务.

VFDT算法假定流数据是确定的，然而这种假设在实际应用中并不总是成立的.由于测量的不精确、数值的缺失及隐私保护等问题，数据不确定性在流数据中普遍存在.例如，在信用卡欺诈检测、环境监测、传感器网络方面，有效信息可能会被不确定的值所掩盖.uVFDTc算法[21](uncertain VFDT classification)在处理不确定数据方面进行了尝试，能够用于解决不确定性数据的分类和数值类型数据的分类.在uVFDTc树的构建过程中，将一个新的不确定训练样本分割成若干个子样本，并从根结点开始，递归划分生成子结点.在叶结点中，从该叶结点的不确定样本中收集到足够的统计信息，对这些统计数据进行Hoeffding检验.如果通过测试，则选择分裂属性并将叶结点拆分为一个内部结点.

针对VFDT算法的存储空间消耗过大的问题，SVFDT算法[23](Strict VFDT)通过在不断降低预测性能的前提下，对树的生长施以强行控制以修改VFDT.SVFDT算法在VFDT的基础上引入了一个函数，该函数可以判断给定的叶子是否应该被分割.当满足VFDT的分割条件时，所有统计数据都会被更新.由于SVFDT创建的树比VFDT要浅，因此SVFDT可以获得更高的处理效率.SVFDT算法可以处理垃圾邮件等大数据量的分类问题.未来若能够将两种算法合成一个整体，可在提高预测精度的同时，确保较低的内存需求和训练时间.

3.2 含概念漂移的分类算法

3.2.1 CVFDT算法

2001年提出了概念自适应的快速决策树CVFDT(Concept adaptive VFDT)算法，该算法在VFDT算法中集成了固定大小的滑动窗口，从而有效解决了概念漂移问题.其中，概念漂移又有虚拟(Virtual)概念漂移和真实(Real)概念漂移之分[24].算法3给出了CVFDT算法的伪代码.

算法3:TreeGenerate CVFDT((X,Y),nijk,ΔG,nmin,w)

Inputs：(X,Y) ——流数据；

nijk——初始化结点统计数；

ΔG——任意结点上选择正确属性的期望概率；

nmin——检查树增长的样例数；

w——窗口大小

Output：HT——决策树

Process：

1.ifW>wthen

2. Forget Example //释放空间

3. Remove Example //从窗口中删除样例

4.endif

5. CVFDTGrow((x,y),HT,δ) //CVFDT增长过程

6. 将(x,y)存入叶子结点L中

7.for(x,y)经过的每个结点Lido

8. 更新各结点的统计信息nijk;

9. 递归调用CVFDTGrow

10.endfor

11.ifL中样例不都属于同一类别 and 在当前结点样例数大于nmin;

12.if选择最佳与次佳分裂属性的信息熵ΔG>εorΔG<ε<τ

13.Aa为最佳分裂属性，Ab为次最佳分裂属性，在结点L中分裂；

14.endif

15.endif

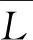
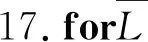
18. 递归调用CheckSplitValidity

19.endfor

20.if属性Aa与Ab的观测值G的差值，即G(Aa)-G(Ab) >ε

21.Aa成为当前的最佳分裂属性

22.endif

由算法3可知，CVFDT算法主要包括四个步骤：树的构建(CVFDTGrow)、释放空间(Forget Example)、样本移除(Remove Example)和分裂检测(Check Split Validity)等四个过程.该算法的主要思想是在VFDT算法的基础上引入滑动窗口，使得建立的决策树能够被不断更新.假设窗口的大小w，在任一时间点n(n通常是当前时间点)，滑动窗口的查询范围表示为{max(0,n-w+1)}.模型使用当前的流数据建立临时子树，之后用新的流数据不断优化建好的决策树.

CVFDT有效地解决了由于流数据样本的不断变化而可能引发的概念漂移问题，且能够反映当前流数据的分布情况，还可以不断更新算法建立的模型.然而，当旧的概念再次出现时，CVFDT需要重新遍历树，使得算法的效率有所下降；其次，CVFDT算法无法自动检测概念漂移的发生.

3.2.2 基于CVFDT的扩展算法

叶爱玲[25]提出了一种多概念自适应快速决策树算法mCVFDT(multiple Concept adaptive VFDT)，该算法采用多重选择机制，将所有最佳预测属性和最近到达属性加入到结点结构中，不需要备选子树.当旧的概念出现时，mCVFDT可从自身结点重新选择合适的子树，避免对树的重复遍历.在选择属性加入结点结构的过程中，将预测属性的精度与当前属性的分类精度进行动态比较，从而实现了概念漂移的检测.相对于CVFDT，mCVFDT在处理大量样本时的性能更佳.然而，mCVFDT算法的实际应用案例缺乏，其性能需要进一步验证.

iOVFDT(incrementally Optimized VFDT)算法[26,27]在VFDT的基础上进行了扩展，提出了针对精度、模型大小和速度的增量优化机制，使VFDT算法能够更好的适应概念漂移.iOVFDT是一种新的增量树归纳方法，具有优化的自适应学习能力的结点划分机制.在树的构建过程中，对每个分裂结点做优化处理，通过对功能叶子的预测实现对精度的监控，通过更新树的结构适应可能存在的概念漂移.相比朴素贝叶斯(Naive Bayes)、加权朴素贝叶斯(Weighted Naive Bayes)等方法，iOVFDT的分类准确度更高.事实上，iOVFDT提供了一种寻找平衡解决方案的机制，它的模型小、内存占用少，同时具有较好的分类精度.

Liu等[28]提出了E-CVFDT(Efficiency CVFDT)的算法，该算法能够处理不同类型的概念漂移.在树的构建过程中，当样本的数目超过窗口大小时，表示窗口已满，此时将对窗口中的所有样本计算信息增益.此外，需要手工指定一个阈值，用于表示最大丢弃的样本数占流入分类模型的样本总数的比重.由于E-CVFDT只对数据分布做了重新分组处理，因此其时间复杂度是线性的.

Ren等[29]提出了iCVFDT算法(imbalanced CVFDT)，该算法通过将CVFDT与一种有效的重采样技术集成，实现类不平衡数据问题的解决.当每个样本(x,y)到达时，首先检查类的分布；若当前到达的样本总数大于滑动窗口的大小w，窗口向前滑动，产生一个以新到达的样本(x,y)为开始的新窗口.iCVFDT分类算法有着与CVFDT类似的稳定性能，同时可适用于不平衡数据的分类处理，如P2P流量数据的分类.

4 研究挑战与方向

从已有研究可以看出，基于决策树的流数据分类算法已经引起了学术界的关注，也有了代表性的研究成果.相对而言，不含概念漂移的流数据分类算法取得了较多的研究成果.然而，基于决策树的流数据分类仍然存在如下几个方面的研究挑战：

首先，由于流数据是现实世界的真实记录，是否包含、何时包含概念漂移不受人为控制.为了实现含有概念漂移的流数据分类，需要在对概念漂移做深入探究的基础上构建可靠的分类算法，做到概念漂移与概念演化(Concept evolution)及异常改变的可靠区分.

其次，流数据不同于静态数据，无法实现完整的持续存储.因此数据标记将是影响流数据分类的突出问题之一[30]，因为基于决策树的流数据分类属于监督学习的范畴，而大量真实数据缺乏有效标记.

最后，现实世界中的数据往往呈现出高维和不平衡特性，同时含有多种冗余信息.因此，从富含冗余信息的高维不平衡数据中提取有用信息，同样极具挑战性.基于稀疏矩阵的数据压缩技术，在去除数据中的无用信息方面具有一定的作用，从而可以实现流数据低维模型的构建.

5 总结

在传统决策树的基础上，针对流数据的独特处理需求，研究流数据分类问题，是数据挖掘领域的重要分支.本文首先简要概述了传统数据挖掘及其主要任务，然后详述了流数据及其特征，特别是突出介绍了概念漂移；接着根据算法是否考察概念漂移，将现有基于决策树的流数据分类算法划分为不含概念漂移的算法和包含概念漂移的算法两大类.就每一类算法，详细介绍算法的基本原理和主要应用，同时指出了其优缺点.最后，指出了基于决策树的流数据分类算法的研究方向.